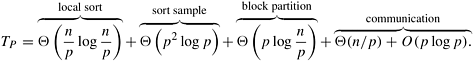Sorting is one of the most common operations performed by a computer. Because sorted data are easier to manipulate than randomly-ordered data, many algorithms require sorted data. Sorting is of additional importance to parallel computing because of its close relation to the task of routing data among processes, which is an essential part of many parallel algorithms. Many parallel sorting algorithms have been investigated for a variety of parallel computer architectures. This chapter presents several parallel sorting algorithms for PRAM, mesh, hypercube, and general shared-address-space and message-passing architectures.
Sorting is defined as the task of arranging an unordered collection of elements into monotonically increasing (or decreasing) order. Specifically, let S = <a1, a2, ..., an > be a sequence of n elements in arbitrary order; sorting transforms S into a monotonically increasing sequence 
such that 
for 1 ≤ i ≤ j ≤ n, and S′ is a permutation of S.
Sorting algorithms are categorized as internal or external. In internal sorting, the number of elements to be sorted is small enough to fit into the process’s main memory. In contrast, external sorting algorithms use auxiliary storage (such as tapes and hard disks) for sorting because the number of elements to be sorted is too large to fit into memory. This chapter concentrates on internal sorting algorithms only.
Sorting algorithms can be categorized as comparison-based and noncomparison-based. A comparison-based algorithm sorts an unordered sequence of elements by repeatedly comparing pairs of elements and, if they are out of order, exchanging them. This fundamental operation of comparison-based sorting is called compare-exchange. The lower bound on the sequential complexity of any sorting algorithms that is comparison-based is Θ(n log n), where n is the number of elements to be sorted. Noncomparison-based algorithms sort by using certain known properties of the elements (such as their binary representation or their distribution). The lower-bound complexity of these algorithms is Θ(n). We concentrate on comparison-based sorting algorithms in this chapter, although we briefly discuss some noncomparison-based sorting algorithms in Section 9.6.
Parallelizing a sequential sorting algorithm involves distributing the elements to be sorted onto the available processes. This process raises a number of issues that we must address in order to make the presentation of parallel sorting algorithms clearer.
In sequential sorting algorithms, the input and the sorted sequences are stored in the process’s memory. However, in parallel sorting there are two places where these sequences can reside. They may be stored on only one of the processes, or they may be distributed among the processes. The latter approach is particularly useful if sorting is an intermediate step in another algorithm. In this chapter, we assume that the input and sorted sequences are distributed among the processes.
Consider the precise distribution of the sorted output sequence among the processes. A general method of distribution is to enumerate the processes and use this enumeration to specify a global ordering for the sorted sequence. In other words, the sequence will be sorted with respect to this process enumeration. For instance, if Pi comes before Pj in the enumeration, all the elements stored in Pi will be smaller than those stored in Pj . We can enumerate the processes in many ways. For certain parallel algorithms and interconnection networks, some enumerations lead to more efficient parallel formulations than others.
A sequential sorting algorithm can easily perform a compare-exchange on two elements because they are stored locally in the process’s memory. In parallel sorting algorithms, this step is not so easy. If the elements reside on the same process, the comparison can be done easily. But if the elements reside on different processes, the situation becomes more complicated.
Consider the case in which each process holds only one element of the sequence to be sorted. At some point in the execution of the algorithm, a pair of processes (Pi, Pj) may need to compare their elements, ai and aj. After the comparison, Pi will hold the smaller and Pj the larger of {ai, aj}. We can perform comparison by having both processes send their elements to each other. Each process compares the received element with its own and retains the appropriate element. In our example, Pi will keep the smaller and Pj will keep the larger of {ai, aj}. As in the sequential case, we refer to this operation as compare-exchange. As Figure 9.1 illustrates, each compare-exchange operation requires one comparison step and one communication step.
Figure 9.1. A parallel compare-exchange operation. Processes Pi and Pj send their elements to each other. Process Pi keeps min{ai, aj}, and Pj keeps max{ai , aj}.
If we assume that processes Pi and Pj are neighbors, and the communication channels are bidirectional, then the communication cost of a compare-exchange step is (ts + tw), where ts and tw are message-startup time and per-word transfer time, respectively. In commercially available message-passing computers, ts is significantly larger than tw, so the communication time is dominated by ts. Note that in today’s parallel computers it takes more time to send an element from one process to another than it takes to compare the elements. Consequently, any parallel sorting formulation that uses as many processes as elements to be sorted will deliver very poor performance because the overall parallel run time will be dominated by interprocess communication.
A general-purpose parallel sorting algorithm must be able to sort a large sequence with a relatively small number of processes. Let p be the number of processes P0, P1, ..., Pp−1, and let n be the number of elements to be sorted. Each process is assigned a block of n/p elements, and all the processes cooperate to sort the sequence. Let A0, A1, ... A p−1 be the blocks assigned to processes P0, P1, ... Pp−1, respectively. We say that Ai ≤ Aj if every element of Ai is less than or equal to every element in Aj. When the sorting algorithm finishes, each process Pi holds a set 
such that 
for i ≤ j, and 
.
As in the one-element-per-process case, two processes Pi and Pj may have to redistribute their blocks of n/p elements so that one of them will get the smaller n/p elements and the other will get the larger n/p elements. Let Ai and Aj be the blocks stored in processes Pi and Pj. If the block of n/p elements at each process is already sorted, the redistribution can be done efficiently as follows. Each process sends its block to the other process. Now, each process merges the two sorted blocks and retains only the appropriate half of the merged block. We refer to this operation of comparing and splitting two sorted blocks as compare-split. The compare-split operation is illustrated in Figure 9.2.
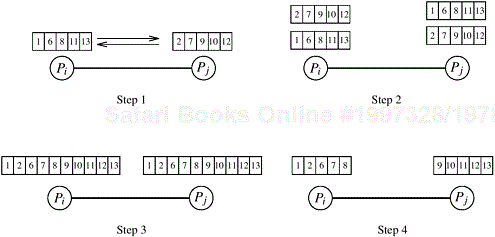
Figure 9.2. A compare-split operation. Each process sends its block of size n/p to the other process. Each process merges the received block with its own block and retains only the appropriate half of the merged block. In this example, process Pi retains the smaller elements and process Pj retains the larger elements.
If we assume that processes Pi and Pj are neighbors and that the communication channels are bidirectional, then the communication cost of a compare-split operation is (ts + twn/p). As the block size increases, the significance of ts decreases, and for sufficiently large blocks it can be ignored. Thus, the time required to merge two sorted blocks of n/p elements is Θ(n/p).
In the quest for fast sorting methods, a number of networks have been designed that sort n elements in time significantly smaller than Θ(n log n). These sorting networks are based on a comparison network model, in which many comparison operations are performed simultaneously.
The key component of these networks is a comparator. A comparator is a device with two inputs x and y and two outputs x′ and y′. For an increasing comparator, x′ = min{x, y} and y′ = max{x, y}; for a decreasing comparator x′ = max{x, y} and y′ = min{x, y}. Figure 9.3 gives the schematic representation of the two types of comparators. As the two elements enter the input wires of the comparator, they are compared and, if necessary, exchanged before they go to the output wires. We denote an increasing comparator by ⊕ and a decreasing comparator by ⊖. A sorting network is usually made up of a series of columns, and each column contains a number of comparators connected in parallel. Each column of comparators performs a permutation, and the output obtained from the final column is sorted in increasing or decreasing order. Figure 9.4 illustrates a typical sorting network. The depth of a network is the number of columns it contains. Since the speed of a comparator is a technology-dependent constant, the speed of the network is proportional to its depth.
Figure 9.3. A schematic representation of comparators: (a) an increasing comparator, and (b) a decreasing comparator.
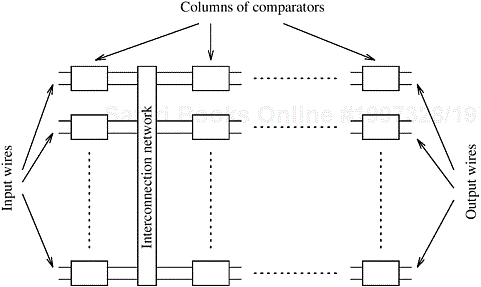
Figure 9.4. A typical sorting network. Every sorting network is made up of a series of columns, and each column contains a number of comparators connected in parallel.
We can convert any sorting network into a sequential sorting algorithm by emulating the comparators in software and performing the comparisons of each column sequentially. The comparator is emulated by a compare-exchange operation, where x and y are compared and, if necessary, exchanged.
The following section describes a sorting network that sorts n elements in Θ(log2 n) time. To simplify the presentation, we assume that n is a power of two.
A bitonic sorting network sorts n elements in Θ(log2 n) time. The key operation of the bitonic sorting network is the rearrangement of a bitonic sequence into a sorted sequence. A bitonic sequence is a sequence of elements <a0, a1, ..., an−1> with the property that either (1) there exists an index i, 0 ≤ i ≤ n − 1, such that <a0, ..., ai > is monotonically increasing and <ai +1, ..., an−1> is monotonically decreasing, or (2) there exists a cyclic shift of indices so that (1) is satisfied. For example, <1, 2, 4, 7, 6, 0> is a bitonic sequence, because it first increases and then decreases. Similarly, <8, 9, 2, 1, 0, 4> is another bitonic sequence, because it is a cyclic shift of <0, 4, 8, 9, 2, 1>.
We present a method to rearrange a bitonic sequence to obtain a monotonically increasing sequence. Let s = <a0, a1, ..., an−1> be a bitonic sequence such that a0 ≤ a1 ≤ ... ≤ an/2−1 and an/2 ≥ an/2+1 ≥ ... ≥ an−1. Consider the following subsequences of s:
In sequence s1, there is an element bi = min{ai, an/2+i} such that all the elements before bi are from the increasing part of the original sequence and all the elements after bi are from the decreasing part. Also, in sequence s2, the element 
is such that all the elements before 
are from the decreasing part of the original sequence and all the elements after are from the increasing part. Thus, the sequences s1 and s2 are bitonic sequences. Furthermore, every element of the first sequence is smaller than every element of the second sequence. The reason is that bi is greater than or equal to all elements of s1, is less than or equal to all elements of s2, and is greater than or equal to bi. Thus, we have reduced the initial problem of rearranging a bitonic sequence of size n to that of rearranging two smaller bitonic sequences and concatenating the results. We refer to the operation of splitting a bitonic sequence of size n into the two bitonic sequences defined by Equation 9.1 as a bitonic split. Although in obtaining s1 and s2 we assumed that the original sequence had increasing and decreasing sequences of the same length, the bitonic split operation also holds for any bitonic sequence (Problem 9.3).
We can recursively obtain shorter bitonic sequences using Equation 9.1 for each of the bitonic subsequences until we obtain subsequences of size one. At that point, the output is sorted in monotonically increasing order. Since after each bitonic split operation the size of the problem is halved, the number of splits required to rearrange the bitonic sequence into a sorted sequence is log n. The procedure of sorting a bitonic sequence using bitonic splits is called bitonic merge. The recursive bitonic merge procedure is illustrated in Figure 9.5.
We now have a method for merging a bitonic sequence into a sorted sequence. This method is easy to implement on a network of comparators. This network of comparators, known as a bitonic merging network, it is illustrated in Figure 9.6. The network contains log n columns. Each column contains n/2 comparators and performs one step of the bitonic merge. This network takes as input the bitonic sequence and outputs the sequence in sorted order. We denote a bitonic merging network with n inputs by ⊕BM[n]. If we replace the ⊕ comparators in Figure 9.6 by ⊖ comparators, the input will be sorted in monotonically decreasing order; such a network is denoted by ⊖BM[n].
![A bitonic merging network for n = 16. The input wires are numbered 0, 1 ..., n − 1, and the binary representation of these numbers is shown. Each column of comparators is drawn separately; the entire figure represents a ⊕BM[16] bitonic merging network. The network takes a bitonic sequence and outputs it in sorted order.](http://imgdetail.ebookreading.net/software_development/21/0201648652/0201648652__introduction-to-parallel__0201648652__graphics__09fig13.gif)
Figure 9.6. A bitonic merging network for n = 16. The input wires are numbered 0, 1 ..., n − 1, and the binary representation of these numbers is shown. Each column of comparators is drawn separately; the entire figure represents a ⊕BM[16] bitonic merging network. The network takes a bitonic sequence and outputs it in sorted order.
Armed with the bitonic merging network, consider the task of sorting n unordered elements. This is done by repeatedly merging bitonic sequences of increasing length, as illustrated in Figure 9.7.
![A schematic representation of a network that converts an input sequence into a bitonic sequence. In this example, ⊕BM[k] and ⊖BM[k] denote bitonic merging networks of input size k that use ⊕ and ⊖ comparators, respectively. The last merging network (⊕BM[16]) sorts the input. In this example, n = 16.](http://imgdetail.ebookreading.net/software_development/21/0201648652/0201648652__introduction-to-parallel__0201648652__graphics__09fig16.gif)
Figure 9.7. A schematic representation of a network that converts an input sequence into a bitonic sequence. In this example, ⊕BM[k] and ⊖BM[k] denote bitonic merging networks of input size k that use ⊕ and ⊖ comparators, respectively. The last merging network (⊕BM[16]) sorts the input. In this example, n = 16.
Let us now see how this method works. A sequence of two elements x and y forms a bitonic sequence, since either x ≤ y, in which case the bitonic sequence has x and y in the increasing part and no elements in the decreasing part, or x ≥ y, in which case the bitonic sequence has x and y in the decreasing part and no elements in the increasing part. Hence, any unsorted sequence of elements is a concatenation of bitonic sequences of size two. Each stage of the network shown in Figure 9.7 merges adjacent bitonic sequences in increasing and decreasing order. According to the definition of a bitonic sequence, the sequence obtained by concatenating the increasing and decreasing sequences is bitonic. Hence, the output of each stage in the network in Figure 9.7 is a concatenation of bitonic sequences that are twice as long as those at the input. By merging larger and larger bitonic sequences, we eventually obtain a bitonic sequence of size n. Merging this sequence sorts the input. We refer to the algorithm embodied in this method as bitonic sort and the network as a bitonic sorting network. The first three stages of the network in Figure 9.7 are shown explicitly in Figure 9.8. The last stage of Figure 9.7 is shown explicitly in Figure 9.6.
Figure 9.8. The comparator network that transforms an input sequence of 16 unordered numbers into a bitonic sequence. In contrast to Figure 9.6, the columns of comparators in each bitonic merging network are drawn in a single box, separated by a dashed line.
The last stage of an n-element bitonic sorting network contains a bitonic merging network with n inputs. This has a depth of log n. The other stages perform a complete sort of n/2 elements. Hence, the depth, d(n), of the network in Figure 9.7 is given by the following recurrence relation:
Solving Equation 9.2, we obtain 
. This network can be implemented on a serial computer, yielding a Θ(n log2 n) sorting algorithm. The bitonic sorting network can also be adapted and used as a sorting algorithm for parallel computers. In the next section, we describe how this can be done for hypercube-and mesh-connected parallel computers.
In this section we discuss how the bitonic sort algorithm can be mapped on general-purpose parallel computers. One of the key aspects of the bitonic algorithm is that it is communication intensive, and a proper mapping of the algorithm must take into account the topology of the underlying interconnection network. For this reason, we discuss how the bitonic sort algorithm can be mapped onto the interconnection network of a hypercube- and mesh-connected parallel computers.
The bitonic sorting network for sorting n elements contains log n stages, and stage i consists of i columns of n/2 comparators. As Figures 9.6 and 9.8 show, each column of comparators performs compare-exchange operations on n wires. On a parallel computer, the compare-exchange function is performed by a pair of processes.
In this mapping, each of the n processes contains one element of the input sequence. Graphically, each wire of the bitonic sorting network represents a distinct process. During each step of the algorithm, the compare-exchange operations performed by a column of comparators are performed by n/2 pairs of processes. One important question is how to map processes to wires in order to minimize the distance that the elements travel during a compare-exchange operation. If the mapping is poor, the elements travel a long distance before they can be compared, which will degrade performance. Ideally, wires that perform a compare-exchange should be mapped onto neighboring processes. Then the parallel formulation of bitonic sort will have the best possible performance over all the formulations that require n processes.
To obtain a good mapping, we must further investigate the way that input wires are paired during each stage of bitonic sort. Consider Figures 9.6 and 9.8, which show the full bitonic sorting network for n = 16. In each of the (1 + log 16)(log 16)/2 = 10 comparator columns, certain wires compare-exchange their elements. Focus on the binary representation of the wire labels. In any step, the compare-exchange operation is performed between two wires only if their labels differ in exactly one bit. During each of the four stages, wires whose labels differ in the least-significant bit perform a compare-exchange in the last step of each stage. During the last three stages, wires whose labels differ in the second-least-significant bit perform a compare-exchange in the second-to-last step of each stage. In general, wires whose labels differ in the ith least-significant bit perform a compare-exchange (log n − i + 1) times. This observation helps us efficiently map wires onto processes by mapping wires that perform compare-exchange operations more frequently to processes that are close to each other.
Hypercube. Mapping wires onto the processes of a hypercube-connected parallel computer is straightforward. Compare-exchange operations take place between wires whose labels differ in only one bit. In a hypercube, processes whose labels differ in only one bit are neighbors (Section 2.4.3). Thus, an optimal mapping of input wires to hypercube processes is the one that maps an input wire with label l to a process with label l where l = 0, 1, ..., n − 1.
Consider how processes are paired for their compare-exchange steps in a d-dimensional hypercube (that is, p = 2d). In the final stage of bitonic sort, the input has been converted into a bitonic sequence. During the first step of this stage, processes that differ only in the dth bit of the binary representation of their labels (that is, the most significant bit) compare-exchange their elements. Thus, the compare-exchange operation takes place between processes along the dth dimension. Similarly, during the second step of the algorithm, the compare-exchange operation takes place among the processes along the (d − 1)th dimension. In general, during the ith step of the final stage, processes communicate along the (d − (i − 1))th dimension. Figure 9.9 illustrates the communication during the last stage of the bitonic sort algorithm.
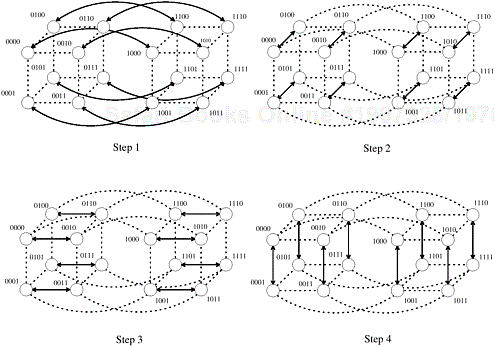
Figure 9.9. Communication during the last stage of bitonic sort. Each wire is mapped to a hypercube process; each connection represents a compare-exchange between processes.
A bitonic merge of sequences of size 2k can be performed on a k-dimensional subcube, with each such sequence assigned to a different subcube (Problem 9.5). Furthermore, during the ith step of this bitonic merge, the processes that compare their elements are neighbors along the (k − (i − 1))th dimension. Figure 9.10 is a modification of Figure 9.7, showing the communication characteristics of the bitonic sort algorithm on a hypercube.
Figure 9.10. Communication characteristics of bitonic sort on a hypercube. During each stage of the algorithm, processes communicate along the dimensions shown.
The bitonic sort algorithm for a hypercube is shown in Algorithm 9.1. The algorithm relies on the functions comp_exchange_max(i) and comp_exchange_min(i). These functions compare the local element with the element on the nearest process along the ith dimension and retain either the minimum or the maximum of the two elements. Problem 9.6 explores the correctness of Algorithm 9.1.
Example 9.1. Parallel formulation of bitonic sort on a hypercube with n = 2d processes. In this algorithm, label is the process’s label and d is the dimension of the hypercube.
1. procedure BITONIC_SORT(label, d) 2. begin 3. for i := 0 to d − 1 do 4. for j := i downto 0 do 5. if (i + 1)st bit of label ≠ jth bit of label then 6. comp_exchange max(j); 7. else 8. comp_exchange min(j); 9. end BITONIC_SORT
During each step of the algorithm, every process performs a compare-exchange operation. The algorithm performs a total of (1 + log n)(log n)/2 such steps; thus, the parallel run time is
This parallel formulation of bitonic sort is cost optimal with respect to the sequential implementation of bitonic sort (that is, the process-time product is Θ(n log2 n)), but it is not cost-optimal with respect to an optimal comparison-based sorting algorithm, which has a serial time complexity of Θ(n log n).
Mesh. Consider how the input wires of the bitonic sorting network can be mapped efficiently onto an n-process mesh. Unfortunately, the connectivity of a mesh is lower than that of a hypercube, so it is impossible to map wires to processes such that each compare-exchange operation occurs only between neighboring processes. Instead, we map wires such that the most frequent compare-exchange operations occur between neighboring processes.
There are several ways to map the input wires onto the mesh processes. Some of these are illustrated in Figure 9.11. Each process in this figure is labeled by the wire that is mapped onto it. Of these three mappings, we concentrate on the row-major shuffled mapping, shown in Figure 9.11(c). We leave the other two mappings as exercises (Problem 9.7).
Figure 9.11. Different ways of mapping the input wires of the bitonic sorting network to a mesh of processes: (a) row-major mapping, (b) row-major snakelike mapping, and (c) row-major shuffled mapping.
The advantage of row-major shuffled mapping is that processes that perform compare-exchange operations reside on square subsections of the mesh whose size is inversely related to the frequency of compare-exchanges. For example, processes that perform compare-exchange during every stage of bitonic sort (that is, those corresponding to wires that differ in the least-significant bit) are neighbors. In general, wires that differ in the ith least-significant bit are mapped onto mesh processes that are 
communication links away. The compare-exchange steps of the last stage of bitonic sort for the row-major shuffled mapping are shown in Figure 9.12. Note that each earlier stage will have only some of these steps.
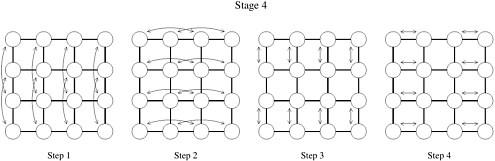
Figure 9.12. The last stage of the bitonic sort algorithm for n = 16 on a mesh, using the row-major shuffled mapping. During each step, process pairs compare-exchange their elements. Arrows indicate the pairs of processes that perform compare-exchange operations.
During the (1 + log n)(log n)/2 steps of the algorithm, processes that are a certain distance apart compare-exchange their elements. The distance between processes determines the communication overhead of the parallel formulation. The total amount of communication performed by each process is 
, which is Θ(
) (Problem 9.7). During each step of the algorithm, each process performs at most one comparison; thus, the total computation performed by each process is Θ(log2 n). This yields a parallel run time of
This is not a cost-optimal formulation, because the process-time product is Θ(n1.5), but the sequential complexity of sorting is Θ(n log n). Although the parallel formulation for a hypercube was optimal with respect to the sequential complexity of bitonic sort, the formulation for mesh is not. Can we do any better? No. When sorting n elements, one per mesh process, for certain inputs the element stored in the process at the upper-left corner will end up in the process at the lower-right corner. For this to happen, this element must travel along 
communication links before reaching its destination. Thus, the run time of sorting on a mesh is bounded by Ω(). Our parallel formulation achieves this lower bound; thus, it is asymptotically optimal for the mesh architecture.
In the parallel formulations of the bitonic sort algorithm presented so far, we assumed there were as many processes as elements to be sorted. Now we consider the case in which the number of elements to be sorted is greater than the number of processes.
Let p be the number of processes and n be the number of elements to be sorted, such that p < n. Each process is assigned a block of n/p elements and cooperates with the other processes to sort them. One way to obtain a parallel formulation with our new setup is to think of each process as consisting of n/p smaller processes. In other words, imagine emulating n/p processes by using a single process. The run time of this formulation will be greater by a factor of n/p because each process is doing the work of n/p processes. This virtual process approach (Section 5.3) leads to a poor parallel implementation of bitonic sort. To see this, consider the case of a hypercube with p processes. Its run time will be Θ((n log2 n)/p), which is not cost-optimal because the process-time product is Θ(n log2 n).
An alternate way of dealing with blocks of elements is to use the compare-split operation presented in Section 9.1. Think of the (n/p)-element blocks as elements to be sorted using compare-split operations. The problem of sorting the p blocks is identical to that of performing a bitonic sort on the p blocks using compare-split operations instead of compare-exchange operations (Problem 9.8). Since the total number of blocks is p, the bitonic sort algorithm has a total of (1 + log p)(log p)/2 steps. Because compare-split operations preserve the initial sorted order of the elements in each block, at the end of these steps the n elements will be sorted. The main difference between this formulation and the one that uses virtual processes is that the n/p elements assigned to each process are initially sorted locally, using a fast sequential sorting algorithm. This initial local sort makes the new formulation more efficient and cost-optimal.
Hypercube. The block-based algorithm for a hypercube with p processes is similar to the one-element-per-process case, but now we have p blocks of size n/p, instead of p elements. Furthermore, the compare-exchange operations are replaced by compare-split operations, each taking Θ(n/p) computation time and Θ(n/p) communication time. Initially the processes sort their n/p elements (using merge sort) in time Θ((n/p) log(n/p)) and then perform Θ(log2 p) compare-split steps. The parallel run time of this formulation is
Because the sequential complexity of the best sorting algorithm is Θ(n log n), the speedup and efficiency are as follows:
From Equation 9.4, for a cost-optimal formulation (log2 p)/(log n) = O(1). Thus, this algorithm can efficiently use up to 
processes. Also from Equation 9.4, the isoefficiency function due to both communication and extra work is Θ(plog p log2 p), which is worse than any polynomial isoefficiency function for sufficiently large p. Hence, this parallel formulation of bitonic sort has poor scalability.
Mesh. The block-based mesh formulation is also similar to the one-element-per-process case. The parallel run time of this formulation is as follows:
Note that comparing the communication overhead of this mesh-based parallel bitonic sort 
to the communication overhead of the hypercube-based formulation (O((n log2 p)/p)), we can see that it is higher by a factor of 
. This factor is smaller than the 
difference in the bisection bandwidth of these architectures. This illustrates that a proper mapping of the bitonic sort on the underlying mesh can achieve better performance than that achieved by simply mapping the hypercube algorithm on the mesh.
The speedup and efficiency are as follows:
Table 9.1. The performance of parallel formulations of bitonic sort for n elements on p processes.
|
Architecture |
Maximum Number of Processes for E = Θ(1) |
Corresponding Parallel Run Time |
Isoefficiency Function |
|---|---|---|---|
|
Hypercube |
|
|
Θ(plog p log2 p) |
|
Mesh |
Θ(log2 n) |
Θ(n/ log n) |
|
|
Ring |
Θ(log n) |
Θ(n) |
Θ(2p p) |
From Equation 9.5, for a cost-optimal formulation 
. Thus, this formulation can efficiently use up to p = Θ(log2 n) processes. Also from Equation 9.5, the isoefficiency function 
. The isoefficiency function of this formulation is exponential, and thus is even worse than that for the hypercube.
From the analysis for hypercube and mesh, we see that parallel formulations of bitonic sort are neither very efficient nor very scalable. This is primarily because the sequential algorithm is suboptimal. Good speedups are possible on a large number of processes only if the number of elements to be sorted is very large. In that case, the efficiency of the internal sorting outweighs the inefficiency of the bitonic sort. Table 9.1 summarizes the performance of bitonic sort on hypercube-, mesh-, and ring-connected parallel computer.
The previous section presented a sorting network that could sort n elements in a time of Θ(log2 n). We now turn our attention to more traditional sorting algorithms. Since serial algorithms with Θ(n log n) time complexity exist, we should be able to use Θ(n) processes to sort n elements in time Θ(log n). As we will see, this is difficult to achieve. We can, however, easily parallelize many sequential sorting algorithms that have Θ(n2) complexity. The algorithms we present are based on bubble sort.
The sequential bubble sort algorithm compares and exchanges adjacent elements in the sequence to be sorted. Given a sequence <a1, a2, ..., an >, the algorithm first performs n − 1 compare-exchange operations in the following order: (a1, a2), (a2, a3), ..., (an−1, an). This step moves the largest element to the end of the sequence. The last element in the transformed sequence is then ignored, and the sequence of compare-exchanges is applied to the resulting sequence 
. The sequence is sorted after n − 1 iterations. We can improve the performance of bubble sort by terminating when no exchanges take place during an iteration. The bubble sort algorithm is shown in Algorithm 9.2.
An iteration of the inner loop of bubble sort takes time Θ(n), and we perform a total of Θ(n) iterations; thus, the complexity of bubble sort is Θ(n2). Bubble sort is difficult to parallelize. To see this, consider how compare-exchange operations are performed during each phase of the algorithm (lines 4 and 5 of Algorithm 9.2). Bubble sort compares all adjacent pairs in order; hence, it is inherently sequential. In the following two sections, we present two variants of bubble sort that are well suited to parallelization.
Example 9.2. Sequential bubble sort algorithm.
1. procedure BUBBLE_SORT(n) 2. begin 3. for i := n − 1 downto 1 do 4. for j := 1 to i do 5. compare-exchange(aj, aj + 1); 6. end BUBBLE_SORT
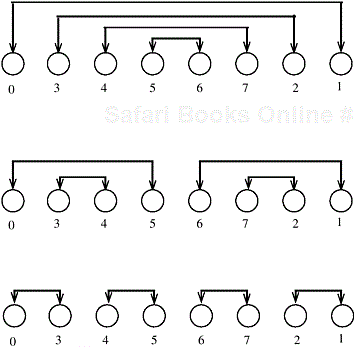
The odd-even transposition algorithm sorts n elements in n phases (n is even), each of which requires n/2 compare-exchange operations. This algorithm alternates between two phases, called the odd and even phases. Let <a1, a2, ..., an> be the sequence to be sorted. During the odd phase, elements with odd indices are compared with their right neighbors, and if they are out of sequence they are exchanged; thus, the pairs (a1, a2), (a3, a4), ..., (an−1, an) are compare-exchanged (assuming n is even). Similarly, during the even phase, elements with even indices are compared with their right neighbors, and if they are out of sequence they are exchanged; thus, the pairs (a2, a3), (a4, a5), ..., (an−2, an−1) are compare-exchanged. After n phases of odd-even exchanges, the sequence is sorted. Each phase of the algorithm (either odd or even) requires Θ(n) comparisons, and there are a total of n phases; thus, the sequential complexity is Θ(n2). The odd-even transposition sort is shown in Algorithm 9.3 and is illustrated in Figure 9.13.
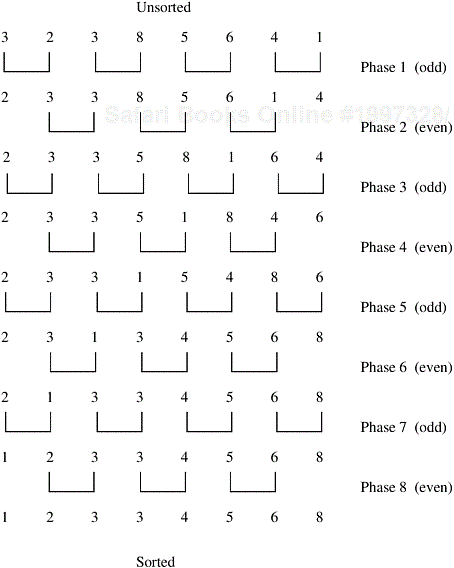
Figure 9.13. Sorting n = 8 elements, using the odd-even transposition sort algorithm. During each phase, n = 8 elements are compared.
Example 9.3. Sequential odd-even transposition sort algorithm.
1. procedure ODD-EVEN(n) 2. begin 3. for i := 1 to n do 4. begin 5. if i is odd then 6. for j := 0 to n/2 − 1 do 7. compare-exchange(a2j + 1, a2j + 2); 8. if i is even then 9. for j := 1 to n/2 − 1 do 10. compare-exchange(a2j, a2j + 1); 11. end for 12. end ODD-EVEN
It is easy to parallelize odd-even transposition sort. During each phase of the algorithm, compare-exchange operations on pairs of elements are performed simultaneously. Consider the one-element-per-process case. Let n be the number of processes (also the number of elements to be sorted). Assume that the processes are arranged in a one-dimensional array. Element ai initially resides on process Pi for i = 1, 2, ..., n. During the odd phase, each process that has an odd label compare-exchanges its element with the element residing on its right neighbor. Similarly, during the even phase, each process with an even label compare-exchanges its element with the element of its right neighbor. This parallel formulation is presented in Algorithm 9.4.
Example 9.4. The parallel formulation of odd-even transposition sort on an n-process ring.
1. procedure ODD-EVEN_PAR (n) 2. begin 3. id := process’s label 4. for i := 1 to n do 5. begin 6. if i is odd then 7. if id is odd then 8. compare-exchange_min(id + 1); 9. else 10. compare-exchange_max(id − 1); 11. if i is even then 12. if id is even then 13. compare-exchange_min(id + 1); 14. else 15. compare-exchange_max(id − 1); 16. end for 17. end ODD-EVEN_PAR
During each phase of the algorithm, the odd or even processes perform a compare- exchange step with their right neighbors. As we know from Section 9.1, this requires time Θ(1). A total of n such phases are performed; thus, the parallel run time of this formulation is Θ(n). Since the sequential complexity of the best sorting algorithm for n elements is Θ(n log n), this formulation of odd-even transposition sort is not cost-optimal, because its process-time product is Θ(n2).
To obtain a cost-optimal parallel formulation, we use fewer processes. Let p be the number of processes, where p < n. Initially, each process is assigned a block of n/p elements, which it sorts internally (using merge sort or quicksort) in Θ((n/p) log(n/p)) time. After this, the processes execute p phases (p/2 odd and p/2 even), performing compare-split operations. At the end of these phases, the list is sorted (Problem 9.10). During each phase, Θ(n/p) comparisons are performed to merge two blocks, and time Θ(n/p) is spent communicating. Thus, the parallel run time of the formulation is
Since the sequential complexity of sorting is Θ(n log n), the speedup and efficiency of this formulation are as follows:
From Equation 9.6, odd-even transposition sort is cost-optimal when p = O(log n). The isoefficiency function of this parallel formulation is Θ(p 2p), which is exponential. Thus, it is poorly scalable and is suited to only a small number of processes.
The main limitation of odd-even transposition sort is that it moves elements only one position at a time. If a sequence has just a few elements out of order, and if they are Θ(n) distance from their proper positions, then the sequential algorithm still requires time Θ(n2) to sort the sequence. To make a substantial improvement over odd-even transposition sort, we need an algorithm that moves elements long distances. Shellsort is one such serial sorting algorithm.
Let n be the number of elements to be sorted and p be the number of processes. To simplify the presentation we will assume that the number of processes is a power of two, that is, p = 2d, but the algorithm can be easily extended to work for an arbitrary number of processes as well. Each process is assigned a block of n/p elements. The processes are considered to be arranged in a logical one-dimensional array, and the ordering of the processes in that array defines the global ordering of the sorted sequence. The algorithm consists of two phases. During the first phase, processes that are far away from each other in the array compare-split their elements. Elements thus move long distances to get close to their final destinations in a few steps. During the second phase, the algorithm switches to an odd-even transposition sort similar to the one described in the previous section. The only difference is that the odd and even phases are performed only as long as the blocks on the processes are changing. Because the first phase of the algorithm moves elements close to their final destinations, the number of odd and even phases performed by the second phase may be substantially smaller than p.
Initially, each process sorts its block of n/p elements internally in Θ(n/p log(n/p)) time. Then, each process is paired with its corresponding process in the reverse order of the array. That is, process Pi, where i < p/2, is paired with process Pp−i −1. Each pair of processes performs a compare-split operation. Next, the processes are partitioned into two groups; one group has the first p/2 processes and the other group has the last p/2 processes. Now, each group is treated as a separate set of p/2 processes and the above scheme of process-pairing is applied to determine which processes will perform the compare-split operation. This process continues for d steps, until each group contains only a single process. The compare-split operations of the first phase are illustrated in Figure 9.14 for d = 3. Note that it is not a direct parallel formulation of the sequential shellsort, but it relies on similar ideas.
In the first phase of the algorithm, each process performs d = log p compare-split operations. In each compare-split operation a total of p/2 pairs of processes need to exchange their locally stored n/p elements. The communication time required by these compare-split operations depend on the bisection bandwidth of the network. In the case in which the bisection bandwidth is Θ(p), the amount of time required by each operation is Θ(n/p). Thus, the complexity of this phase is Θ((n log p)/p). In the second phase, l odd and even phases are performed, each requiring time Θ(n/p). Thus, the parallel run time of the algorithm is
The performance of shellsort depends on the value of l. If l is small, then the algorithm performs significantly better than odd-even transposition sort; if l is Θ(p), then both algorithms perform similarly. Problem 9.13 investigates the worst-case value of l.
All the algorithms presented so far have worse sequential complexity than that of the lower bound for comparison-based sorting, Θ(n log n). This section examines the quicksort algorithm, which has an average complexity of Θ(n log n). Quicksort is one of the most common sorting algorithms for sequential computers because of its simplicity, low overhead, and optimal average complexity.
Quicksort is a divide-and-conquer algorithm that sorts a sequence by recursively dividing it into smaller subsequences. Assume that the n-element sequence to be sorted is stored in the array A[1...n]. Quicksort consists of two steps: divide and conquer. During the divide step, a sequence A[q...r] is partitioned (rearranged) into two nonempty subsequences A[q...s] and A[s + 1...r] such that each element of the first subsequence is smaller than or equal to each element of the second subsequence. During the conquer step, the subsequences are sorted by recursively applying quicksort. Since the subsequences A[q...s] and A[s + 1...r] are sorted and the first subsequence has smaller elements than the second, the entire sequence is sorted.
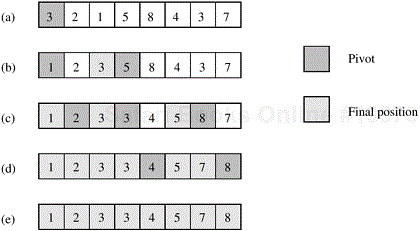
How is the sequence A[q...r] partitioned into two parts – one with all elements smaller than the other? This is usually accomplished by selecting one element x from A[q...r] and using this element to partition the sequence A[q...r] into two parts – one with elements less than or equal to x and the other with elements greater than x.Element x is called the pivot. The quicksort algorithm is presented in Algorithm 9.5. This algorithm arbitrarily chooses the first element of the sequence A[q...r] as the pivot. The operation of quicksort is illustrated in Figure 9.15.
Example 9.5. The sequential quicksort algorithm.
1. procedure QUICKSORT (A, q, r) 2. begin 3. if q < r then 4. begin 5. x := A[q]; 6. s := q; 7. for i := q + 1 to r do 8. if A[i]≤x then 9. begin 10. s := s + 1; 11. swap(A[s], A[i]); 12. end if 13. swap(A[q], A[s]); 14. QUICKSORT (A, q, s); 15. QUICKSORT (A, s + 1, r); 16. end if 17. end QUICKSORT
The complexity of partitioning a sequence of size k is Θ(k). Quicksort’s performance is greatly affected by the way it partitions a sequence. Consider the case in which a sequence of size k is split poorly, into two subsequences of sizes 1 and k − 1. The run time in this case is given by the recurrence relation T(n) = T(n − 1) + Θ(n), whose solution is T(n) = Θ(n2). Alternatively, consider the case in which the sequence is split well, into two roughly equal-size subsequences of 
and 
elements. In this case, the run time is given by the recurrence relation T(n) = 2T(n/2) + Θ(n), whose solution is T(n) = Θ(n log n). The second split yields an optimal algorithm. Although quicksort can have O(n2) worst-case complexity, its average complexity is significantly better; the average number of compare-exchange operations needed by quicksort for sorting a randomly-ordered input sequence is 1.4n log n, which is asymptotically optimal. There are several ways to select pivots. For example, the pivot can be the median of a small number of elements of the sequence, or it can be an element selected at random. Some pivot selection strategies have advantages over others for certain input sequences.
Quicksort can be parallelized in a variety of ways. First, consider a naive parallel formulation that was also discussed briefly in Section 3.2.1 in the context of recursive decomposition. Lines 14 and 15 of Algorithm 9.5 show that, during each call of QUICKSORT, the array is partitioned into two parts and each part is solved recursively. Sorting the smaller arrays represents two completely independent subproblems that can be solved in parallel. Therefore, one way to parallelize quicksort is to execute it initially on a single process; then, when the algorithm performs its recursive calls (lines 14 and 15), assign one of the subproblems to another process. Now each of these processes sorts its array by using quicksort and assigns one of its subproblems to other processes. The algorithm terminates when the arrays cannot be further partitioned. Upon termination, each process holds an element of the array, and the sorted order can be recovered by traversing the processes as we will describe later. This parallel formulation of quicksort uses n processes to sort n elements. Its major drawback is that partitioning the array A[q ...r ] into two smaller arrays, A[q ...s] and A[s + 1 ...r ], is done by a single process. Since one process must partition the original array A[1 ...n], the run time of this formulation is bounded below by Ω(n). This formulation is not cost-optimal, because its process-time product is Ω(n2).
The main limitation of the previous parallel formulation is that it performs the partitioning step serially. As we will see in subsequent formulations, performing partitioning in parallel is essential in obtaining an efficient parallel quicksort. To see why, consider the recurrence equation T (n) = 2T (n/2) + Θ(n), which gives the complexity of quicksort for optimal pivot selection. The term Θ(n) is due to the partitioning of the array. Compare this complexity with the overall complexity of the algorithm, Θ(n log n). From these two complexities, we can think of the quicksort algorithm as consisting of Θ(log n) steps, each requiring time Θ(n) – that of splitting the array. Therefore, if the partitioning step is performed in time Θ(1), using Θ(n) processes, it is possible to obtain an overall parallel run time of Θ(log n), which leads to a cost-optimal formulation. However, without parallelizing the partitioning step, the best we can do (while maintaining cost-optimality) is to use only Θ(log n) processes to sort n elements in time Θ(n) (Problem 9.14). Hence, parallelizing the partitioning step has the potential to yield a significantly faster parallel formulation.
In the previous paragraph, we hinted that we could partition an array of size n into two smaller arrays in time Θ(1) by using Θ(n) processes. However, this is difficult for most parallel computing models. The only known algorithms are for the abstract PRAM models. Because of communication overhead, the partitioning step takes longer than Θ(1) on realistic shared-address-space and message-passing parallel computers. In the following sections we present three distinct parallel formulations: one for a CRCW PRAM, one for a shared-address-space architecture, and one for a message-passing platform. Each of these formulations parallelizes quicksort by performing the partitioning step in parallel.
We will now present a parallel formulation of quicksort for sorting n elements on an n-process arbitrary CRCW PRAM. Recall from Section 2.4.1 that an arbitrary CRCW PRAM is a concurrent-read, concurrent-write parallel random-access machine in which write conflicts are resolved arbitrarily. In other words, when more than one process tries to write to the same memory location, only one arbitrarily chosen process is allowed to write, and the remaining writes are ignored.
Executing quicksort can be visualized as constructing a binary tree. In this tree, the pivot is the root; elements smaller than or equal to the pivot go to the left subtree, and elements larger than the pivot go to the right subtree. Figure 9.16 illustrates the binary tree constructed by the execution of the quicksort algorithm illustrated in Figure 9.15. The sorted sequence can be obtained from this tree by performing an in-order traversal. The PRAM formulation is based on this interpretation of quicksort.
Figure 9.16. A binary tree generated by the execution of the quicksort algorithm. Each level of the tree represents a different array-partitioning iteration. If pivot selection is optimal, then the height of the tree is Θ(log n), which is also the number of iterations.
The algorithm starts by selecting a pivot element and partitioning the array into two parts – one with elements smaller than the pivot and the other with elements larger than the pivot. Subsequent pivot elements, one for each new subarray, are then selected in parallel. This formulation does not rearrange elements; instead, since all the processes can read the pivot in constant time, they know which of the two subarrays (smaller or larger) the elements assigned to them belong to. Thus, they can proceed to the next iteration.
The algorithm that constructs the binary tree is shown in Algorithm 9.6. The array to be sorted is stored in A[1...n] and process i is assigned element A[i]. The arrays leftchild[1...n] and rightchild[1...n] keep track of the children of a given pivot. For each process, the local variable parenti stores the label of the process whose element is the pivot. Initially, all the processes write their process labels into the variable root in line 5. Because the concurrent write operation is arbitrary, only one of these labels will actually be written into root. The value A[root] is used as the first pivot and root is copied into parenti for each process i . Next, processes that have elements smaller than A[parenti] write their process labels into leftchild[parenti], and those with larger elements write their process label into rightchild[parenti]. Thus, all processes whose elements belong in the smaller partition have written their labels into leftchild[parenti], and those with elements in the larger partition have written their labels into rightchild[parenti]. Because of the arbitrary concurrent-write operations, only two values – one for leftchild[parenti] and one for rightchild[parenti] – are written into these locations. These two values become the labels of the processes that hold the pivot elements for the next iteration, in which two smaller arrays are being partitioned. The algorithm continues until n pivot elements are selected. A process exits when its element becomes a pivot. The construction of the binary tree is illustrated in Figure 9.17. During each iteration of the algorithm, a level of the tree is constructed in time Θ(1). Thus, the average complexity of the binary tree building algorithm is Θ(log n) as the average height of the tree is Θ(log n) (Problem 9.16).
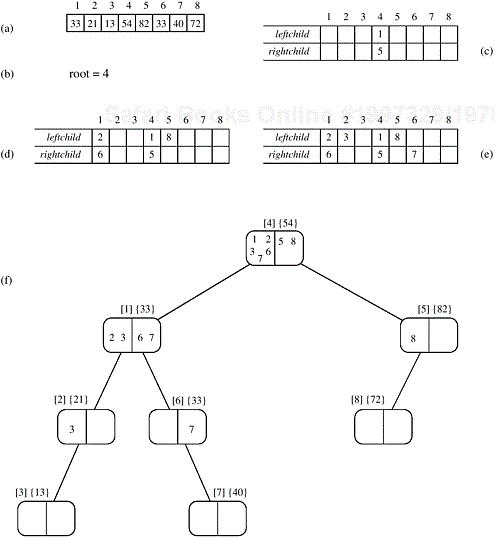
Figure 9.17. The execution of the PRAM algorithm on the array shown in (a). The arrays leftchild and rightchild are shown in (c), (d), and (e) as the algorithm progresses. Figure (f) shows the binary tree constructed by the algorithm. Each node is labeled by the process (in square brackets), and the element is stored at that process (in curly brackets). The element is the pivot. In each node, processes with smaller elements than the pivot are grouped on the left side of the node, and those with larger elements are grouped on the right side. These two groups form the two partitions of the original array. For each partition, a pivot element is selected at random from the two groups that form the children of the node.
Example 9.6. The binary tree construction procedure for the CRCW PRAM parallel quicksort formulation.
1. procedure BUILD TREE (A[1...n]) 2. begin 3. for each process i do 4. begin 5. root := i; 6. parenti := root; 7. leftchild[i] := rightchild[i] := n + 1; 8. end for 9. repeat for each process i ≠ r oot do 10. begin 11. if (A[i] < A[parenti]) or (A[i]= A[parenti] and i <parenti) then 12. begin 13. leftchild[parenti] :=i ; 14. if i = leftchild[parenti] then exit 15. else parenti := leftchild[parenti]; 16. end for 17. else 18. begin 19. rightchild[parenti] :=i; 20. if i = rightchild[parenti] then exit 21. else parenti := rightchild[parenti]; 22. end else 23. end repeat 24. end BUILD_TREE
After building the binary tree, the algorithm determines the position of each element in the sorted array. It traverses the tree and keeps a count of the number of elements in the left and right subtrees of any element. Finally, each element is placed in its proper position in time Θ(1), and the array is sorted. The algorithm that traverses the binary tree and computes the position of each element is left as an exercise (Problem 9.15). The average run time of this algorithm is Θ(log n) on an n-process PRAM. Thus, its overall process-time product is Θ(n log n), which is cost-optimal.
We now turn our attention to a more realistic parallel architecture – that of a p-process system connected via an interconnection network. Initially, our discussion will focus on developing an algorithm for a shared-address-space system and then we will show how this algorithm can be adapted to message-passing systems.
The quicksort formulation for a shared-address-space system works as follows. Let A be an array of n elements that need to be sorted and p be the number of processes. Each process is assigned a consecutive block of n/p elements, and the labels of the processes define the global order of the sorted sequence. Let Ai be the block of elements assigned to process Pi .
The algorithm starts by selecting a pivot element, which is broadcast to all processes. Each process Pi, upon receiving the pivot, rearranges its assigned block of elements into two sub-blocks, one with elements smaller than the pivot Si and one with elements larger than the pivot Li. This local rearrangement is done in place using the collapsing the loops approach of quicksort. The next step of the algorithm is to rearrange the elements of the original array A so that all the elements that are smaller than the pivot (i.e., 
) are stored at the beginning of the array, and all the elements that are larger than the pivot (i.e., 
) are stored at the end of the array.
Once this global rearrangement is done, then the algorithm proceeds to partition the processes into two groups, and assign to the first group the task of sorting the smaller elements S, and to the second group the task of sorting the larger elements L . Each of these steps is performed by recursively calling the parallel quicksort algorithm. Note that by simultaneously partitioning both the processes and the original array each group of processes can proceed independently. The recursion ends when a particular sub-block of elements is assigned to only a single process, in which case the process sorts the elements using a serial quicksort algorithm.
The partitioning of processes into two groups is done according to the relative sizes of the S and L blocks. In particular, the first 
processes are assigned to sort the smaller elements S, and the rest of the processes are assigned to sort the larger elements L. Note that the 0.5 term in the above formula is to ensure that the processes are assigned in the most balanced fashion.
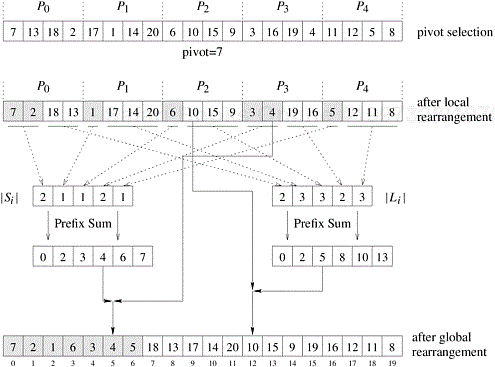
Example 9.1 Efficient parallel quicksort
Figure 9.18 illustrates this algorithm using an example of 20 integers and five processes. In the first step, each process locally rearranges the four elements that it is initially responsible for, around the pivot element (seven in this example), so that the elements smaller or equal to the pivot are moved to the beginning of the locally assigned portion of the array (and are shaded in the figure). Once this local rearrangement is done, the processes perform a global rearrangement to obtain the third array shown in the figure (how this is performed will be discussed shortly). In the second step, the processes are partitioned into two groups. The first contains {P0, P1} and is responsible for sorting the elements that are smaller than or equal to seven, and the second group contains processes {P2, P3, P4} and is responsible for sorting the elements that are greater than seven. Note that the sizes of these process groups were created to match the relative size of the smaller than and larger than the pivot arrays. Now, the steps of pivot selection, local, and global rearrangement are recursively repeated for each process group and sub-array, until a sub-array is assigned to a single process, in which case it proceeds to sort it locally. Also note that these final local sub-arrays will in general be of different size, as they depend on the elements that were selected to act as pivots. ▪
In order to globally rearrange the elements of A into the smaller and larger sub-arrays we need to know where each element of A will end up going at the end of that rearrangement. One way of doing this rearrangement is illustrated at the bottom of Figure 9.19. In this approach, S is obtained by concatenating the various Si blocks over all the processes, in increasing order of process label. Similarly, L is obtained by concatenating the various Li blocks in the same order. As a result, for process Pi, the j th element of its Si sub-block will be stored at location 
, and the j th element of its Li sub-block will be stored at location 
.
These locations can be easily computed using the prefix-sum operation described in Section 4.3. Two prefix-sums are computed, one involving the sizes of the Si sub-blocks and the other the sizes of the Li sub-blocks. Let Q and R be the arrays of size p that store these prefix sums, respectively. Their elements will be
Note that for each process Pi, Qi is the starting location in the final array where its lower-than-the-pivot element will be stored, and Ri is the ending location in the final array where its greater-than-the-pivot elements will be stored. Once these locations have been determined, the overall rearrangement of A can be easily performed by using an auxiliary array A′ of size n. These steps are illustrated in Figure 9.19. Note that the above definition of prefix-sum is slightly different from that described in Section 4.3, in the sense that the value that is computed for location Qi (or Ri) does not include Si (or Li) itself. This type of prefix-sum is sometimes referred to as non-inclusive prefix-sum.
Analysis. The complexity of the shared-address-space formulation of the quicksort algorithm depends on two things. The first is the amount of time it requires to split a particular array into the smaller-than- and the greater-than-the-pivot sub-arrays, and the second is the degree to which the various pivots being selected lead to balanced partitions. In this section, to simplify our analysis, we will assume that pivot selection always results in balanced partitions. However, the issue of proper pivot selection and its impact on the overall parallel performance is addressed in Section 9.4.4.
Given an array of n elements and p processes, the shared-address-space formulation of the quicksort algorithm needs to perform four steps: (i) determine and broadcast the pivot; (ii) locally rearrange the array assigned to each process; (iii) determine the locations in the globally rearranged array that the local elements will go to; and (iv) perform the global rearrangement. The first step can be performed in time Θ(log p) using an efficient recursive doubling approach for shared-address-space broadcast. The second step can be done in time Θ(n/p) using the traditional quicksort algorithm for splitting around a pivot element. The third step can be done in Θ(log p) using two prefix sum operations. Finally, the fourth step can be done in at least time Θ(n/p) as it requires us to copy the local elements to their final destination. Thus, the overall complexity of splitting an n-element array is Θ(n/p) + Θ(log p). This process is repeated for each of the two subarrays recursively on half the processes, until the array is split into p parts, at which point each process sorts the elements of the array assigned to it using the serial quicksort algorithm. Thus, the overall complexity of the parallel algorithm is:
The communication overhead in the above formulation is reflected in the Θ(log2 p) term, which leads to an overall isoefficiency of Θ(p log2 p). It is interesting to note that the overall scalability of the algorithm is determined by the amount of time required to perform the pivot broadcast and the prefix sum operations.
The quicksort formulation for message-passing systems follows the general structure of the shared-address-space formulation. However, unlike the shared-address-space case in which array A and the globally rearranged array A′ are stored in shared memory and can be accessed by all the processes, these arrays are now explicitly distributed among the processes. This makes the task of splitting A somewhat more involved.
In particular, in the message-passing version of the parallel quicksort, each process stores n/p elements of array A. This array is also partitioned around a particular pivot element using a two-phase approach. In the first phase (which is similar to the shared-address-space formulation), the locally stored array Ai at process Pi is partitioned into the smaller-than- and larger-than-the-pivot sub-arrays Si and Li locally. In the next phase, the algorithm first determines which processes will be responsible for recursively sorting the smaller-than-the-pivot sub-arrays (i.e., 
) and which process will be responsible for recursively sorting the larger-than-the-pivot sub-arrays (i.e., 
). Once this is done, then the processes send their Si and Li arrays to the corresponding processes. After that, the processes are partitioned into the two groups, one for S and one for L, and the algorithm proceeds recursively. The recursion terminates when each sub-array is assigned to a single process, at which point it is sorted locally.
The method used to determine which processes will be responsible for sorting S and L is identical to that for the shared-address-space formulation, which tries to partition the processes to match the relative size of the two sub-arrays. Let pS and pL be the number of processes assigned to sort S and L, respectively. Each one of the pS processes will end up storing |S|/pS elements of the smaller-than-the-pivot sub-array, and each one of the pL processes will end up storing |L|/pL elements of the larger-than-the-pivot sub-array. The method used to determine where each process Pi will send its Si and Li elements follows the same overall strategy as the shared-address-space formulation. That is, the various Si (or Li) sub-arrays will be stored in consecutive locations in S (or L) based on the process number. The actual processes that will be responsible for these elements are determined by the partition of S (or L) into pS (or pL) equal-size segments, and can be computed using a prefix-sum operation. Note that each process Pi may need to split its Si (or Li) sub-arrays into multiple segments and send each one to different processes. This can happen because its elements may be assigned to locations in S (or L) that span more than one process. In general, each process may have to send its elements to two different processes; however, there may be cases in which more than two partitions are required.
Analysis. Our analysis of the message-passing formulation of quicksort will mirror the corresponding analysis of the shared-address-space formulation.
Consider a message-passing parallel computer with p processes and O (p) bisection bandwidth. The amount of time required to split an array of size n is Θ(log p) for broadcasting the pivot element, Θ(n/p) for splitting the locally assigned portion of the array, Θ(log p) for performing the prefix sums to determine the process partition sizes and the destinations of the various Si and Li sub-arrays, and the amount of time required for sending and receiving the various arrays. This last step depends on how the processes are mapped on the underlying architecture and on the maximum number of processes that each process needs to communicate with. In general, this communication step involves all-to-all personalized communication (because a particular process may end-up receiving elements from all other processes), whose complexity has a lower bound of Θ(n/p). Thus, the overall complexity for the split is Θ(n/p) + Θ(log p), which is asymptotically similar to that of the shared-address-space formulation. As a result, the overall runtime is also the same as in Equation 9.8, and the algorithm has a similar isoefficiency function of Θ(p log2 p).
In the parallel quicksort algorithm, we glossed over pivot selection. Pivot selection is particularly difficult, and it significantly affects the algorithm’s performance. Consider the case in which the first pivot happens to be the largest element in the sequence. In this case, after the first split, one of the processes will be assigned only one element, and the remaining p − 1 processes will be assigned n − 1 elements. Hence, we are faced with a problem whose size has been reduced only by one element but only p − 1 processes will participate in the sorting operation. Although this is a contrived example, it illustrates a significant problem with parallelizing the quicksort algorithm. Ideally, the split should be done such that each partition has a non-trivial fraction of the original array.
One way to select pivots is to choose them at random as follows. During the ith split, one process in each of the process groups randomly selects one of its elements to be the pivot for this partition. This is analogous to the random pivot selection in the sequential quicksort algorithm. Although this method seems to work for sequential quicksort, it is not well suited to the parallel formulation. To see this, consider the case in which a bad pivot is selected at some point. In sequential quicksort, this leads to a partitioning in which one subsequence is significantly larger than the other. If all subsequent pivot selections are good, one poor pivot will increase the overall work by at most an amount equal to the length of the subsequence; thus, it will not significantly degrade the performance of sequential quicksort. In the parallel formulation, however, one poor pivot may lead to a partitioning in which a process becomes idle, and that will persist throughout the execution of the algorithm.
If the initial distribution of elements in each process is uniform, then a better pivot selection method can be derived. In this case, the n/p elements initially stored at each process form a representative sample of all n elements. In other words, the median of each n/p-element subsequence is very close to the median of the entire n-element sequence. Why is this a good pivot selection scheme under the assumption of identical initial distributions? Since the distribution of elements on each process is the same as the overall distribution of the n elements, the median selected to be the pivot during the first step is a good approximation of the overall median. Since the selected pivot is very close to the overall median, roughly half of the elements in each process are smaller and the other half larger than the pivot. Therefore, the first split leads to two partitions, such that each of them has roughly n/2 elements. Similarly, the elements assigned to each process of the group that is responsible for sorting the smaller-than-the-pivot elements (and the group responsible for sorting the larger-than-the-pivot elements) have the same distribution as the n/2 smaller (or larger) elements of the original list. Thus, the split not only maintains load balance but also preserves the assumption of uniform element distribution in the process group. Therefore, the application of the same pivot selection scheme to the sub-groups of processes continues to yield good pivot selection.
Can we really assume that the n/p elements in each process have the same distribution as the overall sequence? The answer depends on the application. In some applications, either the random or the median pivot selection scheme works well, but in others neither scheme delivers good performance. Two additional pivot selection schemes are examined in Problems 9.20 and 9.21.
A popular serial algorithm for sorting an array of n elements whose values are uniformly distributed over an interval [a, b] is the bucket sort algorithm. In this algorithm, the interval [a, b] is divided into m equal-sized subintervals referred to as buckets, and each element is placed in the appropriate bucket. Since the n elements are uniformly distributed over the interval [a, b], the number of elements in each bucket is roughly n/m. The algorithm then sorts the elements in each bucket, yielding a sorted sequence. The run time of this algorithm is Θ(n log(n/m)).Form = Θ(n), it exhibits linear run time, Θ(n). Note that the reason that bucket sort can achieve such a low complexity is because it assumes that the n elements to be sorted are uniformly distributed over an interval [a, b].
Parallelizing bucket sort is straightforward. Let n be the number of elements to be sorted and p be the number of processes. Initially, each process is assigned a block of n/p elements, and the number of buckets is selected to be m = p. The parallel formulation of bucket sort consists of three steps. In the first step, each process partitions its block of n/p elements into p sub-blocks, one for each of the p buckets. This is possible because each process knows the interval [a, b) and thus the interval for each bucket. In the second step, each process sends sub-blocks to the appropriate processes. After this step, each process has only the elements belonging to the bucket assigned to it. In the third step, each process sorts its bucket internally by using an optimal sequential sorting algorithm.
Unfortunately, the assumption that the input elements are uniformly distributed over an interval [a, b] is not realistic. In most cases, the actual input may not have such a distribution or its distribution may be unknown. Thus, using bucket sort may result in buckets that have a significantly different number of elements, thereby degrading performance. In such situations an algorithm called sample sort will yield significantly better performance. The idea behind sample sort is simple. A sample of size s is selected from the n-element sequence, and the range of the buckets is determined by sorting the sample and choosing m − 1 elements from the result. These elements (called splitters) divide the sample into m equal-sized buckets. After defining the buckets, the algorithm proceeds in the same way as bucket sort. The performance of sample sort depends on the sample size s and the way it is selected from the n-element sequence.
Consider a splitter selection scheme that guarantees that the number of elements ending up in each bucket is roughly the same for all buckets. Let n be the number of elements to be sorted and m be the number of buckets. The scheme works as follows. It divides the n elements into m blocks of size n/m each, and sorts each block by using quicksort. From each sorted block it chooses m − 1 evenly spaced elements. The m(m − 1) elements selected from all the blocks represent the sample used to determine the buckets. This scheme guarantees that the number of elements ending up in each bucket is less than 2n/m (Problem 9.28).
How can we parallelize the splitter selection scheme? Let p be the number of processes. As in bucket sort, set m = p; thus, at the end of the algorithm, each process contains only the elements belonging to a single bucket. Each process is assigned a block of n/p elements, which it sorts sequentially. It then chooses p − 1 evenly spaced elements from the sorted block. Each process sends its p − 1 sample elements to one process – say P0. Process P0 then sequentially sorts the p(p − 1) sample elements and selects the p − 1 splitters. Finally, process P0 broadcasts the p − 1 splitters to all the other processes. Now the algorithm proceeds in a manner identical to that of bucket sort. This algorithm is illustrated in Figure 9.20.
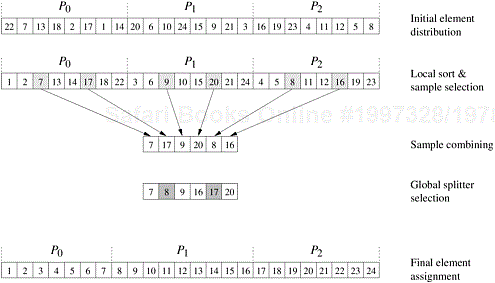
Figure 9.20. An example of the execution of sample sort on an array with 24 elements on three processes.
Analysis. We now analyze the complexity of sample sort on a message-passing computer with p processes and O (p) bisection bandwidth.
The internal sort of n/p elements requires time Θ((n/p) log(n/p)), and the selection of p − 1 sample elements requires time Θ(p). Sending p − 1 elements to process P0 is similar to a gather operation (Section 4.4); the time required is Θ(p2). The time to internally sort the p(p − 1) sample elements at P0 is Θ(p2 log p), and the time to select p − 1 splitters is Θ(p). The p − 1 splitters are sent to all the other processes by using one-to-all broadcast (Section 4.1), which requires time Θ(p log p). Each process can insert these p − 1 splitters in its local sorted block of size n/p by performing p − 1 binary searches. Each process thus partitions its block into p sub-blocks, one for each bucket. The time required for this partitioning is Θ(p log(n/p)). Each process then sends sub-blocks to the appropriate processes (that is, buckets). The communication time for this step is difficult to compute precisely, as it depends on the size of the sub-blocks to be communicated. These sub-blocks can vary arbitrarily between 0 and n/p. Thus, the upper bound on the communication time is O (n) + O (p log p).
If we assume that the elements stored in each process are uniformly distributed, then each sub-block has roughly Θ(n/p2) elements. In this case, the parallel run time is
In this case, the isoefficiency function is Θ(p3 log p). If bitonic sort is used to sort the p(p − 1) sample elements, then the time for sorting the sample would be Θ(p log p), and the isoefficiency will be reduced to Θ(p2 log p) (Problem 9.30).
As mentioned in the introduction to this chapter, there are many sorting algorithms, and we cannot explore them all in this chapter. However, in this section we briefly present two additional sorting algorithms that are important both practically and theoretically. Our discussion of these schemes will be brief. Refer to the bibliographic remarks (Section 9.7) for references on these and other algorithms.
All the sorting algorithms presented so far are based on compare-exchange operations. This section considers an algorithm based on enumeration sort, which does not use compare-exchange. The basic idea behind enumeration sort is to determine the rank of each element. The rank of an element ai is the number of elements smaller than ai in the sequence to be sorted. The rank of ai can be used to place it in its correct position in the sorted sequence. Several parallel algorithms are based on enumeration sort. Here we present one such algorithm that is suited to the CRCW PRAM model. This formulation sorts n elements by using n2 processes in time Θ(1).
Assume that concurrent writes to the same memory location of the CRCW PRAM result in the sum of all the values written being stored at that location (Section 2.4.1). Consider the n2 processes as being arranged in a two-dimensional grid. The algorithm consists of two steps. During the first step, each column j of processes computes the number of elements smaller than aj . During the second step, each process P1,j of the first row places aj in its proper position as determined by its rank. The algorithm is shown in Algorithm 9.7. It uses an auxiliary array C [1...n] to store the rank of each element. The crucial steps of this algorithm are lines 7 and 9. There, each process Pi,j, writes 1 in C [j] if the element A[i] is smaller than A[j] and writes 0 otherwise. Because of the additive-write conflict resolution scheme, the effect of these instructions is to count the number of elements smaller than A[j] and thus compute its rank. The run time of this algorithm is Θ(1). Modifications of this algorithm for various parallel architectures are discussed in Problem 9.26.
Example 9.7. Enumeration sort on a CRCW PRAM with additive-write conflict resolution.
1. procedure ENUM SORT (n) 2. begin 3. for each process P1,j do 4. C[j] :=0; 5. for each process Pi,j do 6. if (A[i] < A[j]) or ( A[i]= A[j] and i < j) then 7. C[j] := 1; 8. else 9. C[j] := 0; 10. for each process P1,j do 11. A[C[j]] := A[j]; 12. end ENUM_SORT
The radix sort algorithm relies on the binary representation of the elements to be sorted. Let b be the number of bits in the binary representation of an element. The radix sort algorithm examines the elements to be sorted r bits at a time, where r < b. Radix sort requires b/r iterations. During iteration i , it sorts the elements according to their ith least significant block of r bits. For radix sort to work properly, each of the b/r sorts must be stable. A sorting algorithm is stable if its output preserves the order of input elements with the same value. Radix sort is stable if it preserves the input order of any two r -bit blocks when these blocks are equal. The most common implementation of the intermediate b/r radix-2r sorts uses enumeration sort (Section 9.6.1) because the range of possible values [0...2r − 1] is small. For such cases, enumeration sort significantly outperforms any comparison-based sorting algorithm.
Consider a parallel formulation of radix sort for n elements on a message-passing computer with n processes. The parallel radix sort algorithm is shown in Algorithm 9.8. The main loop of the algorithm (lines 3–17) performs the b/r enumeration sorts of the r-bit blocks. The enumeration sort is performed by using the prefix_sum() and parallel_sum() functions. These functions are similar to those described in Sections 4.1 and 4.3. During each iteration of the inner loop (lines 6–15), radix sort determines the position of the elements with an r-bit value of j . It does this by summing all the elements with the same value and then assigning them to processes. The variable rank holds the position of each element. At the end of the loop (line 16), each process sends its element to the appropriate process. Process labels determine the global order of sorted elements.
Example 9.8. A parallel radix sort algorithm, in which each element of the array A[1...n] to be sorted is assigned to one process. The function prefix sum() computes the prefix sum of the flag variable, and the function parallel sum() returns the total sum of the flag variable.
1. procedure RADIX SORT(A, r) 2. begin 3. for i := 0 to b/r − 1 do 4. begin 5. offset := 0; 6. for j := 0 to 2r − 1 do 7. begin 8. flag := 0; 9. if the ith least significant r-bit block of A[Pk] = j then 10. flag := 1; 11. index := prefix_sum(flag) 12. if flag = 1 then 13. rank := offset + index; 14. offset := parallel_sum(flag); 15. endfor 16. each process Pk send its element A[Pk] to process Prank; 17. endfor 18. end RADIX_SORT
As shown in Sections 4.1 and 4.3, the complexity of both the parallel_sum() and prefix_sum() operations is Θ(log n) on a message-passing computer with n processes. The complexity of the communication step on line 16 is Θ(n). Thus, the parallel run time of this algorithm is
![A parallel radix sort algorithm, in which each element of the array A[1...n] to be sorted is assigned to one process. The function prefix sum() computes the prefix sum of the flag variable, and the function parallel sum() returns the total sum of the flag variable.](http://imgdetail.ebookreading.net/software_development/21/0201648652/0201648652__introduction-to-parallel__0201648652__graphics__09fig62.gif){kind=small}
Knuth [Knu73] discusses sorting networks and their history. The question of whether a sorting network could sort n elements in time O (log n) remained open for a long time. In 1983, Ajtai, Komlos, and Szemeredi [AKS83] discovered a sorting network that could sort n elements in time O (log n) by using O (n log n) comparators. Unfortunately, the constant of their sorting network is quite large (many thousands), and thus is not practical. The bitonic sorting network was discovered by Batcher [Bat68], who also discovered the network for odd-even sort. These were the first networks capable of sorting n elements in time O (log2 n). Stone [Sto71] maps the bitonic sort onto a perfect-shuffle interconnection network, sorting n elements by using n processes in time O (log2 n). Siegel [Sie77]shows that bitonic sort can also be performed on the hypercube in time O (log2 n). The block-based hypercube formulation of bitonic sort is discussed in Johnsson [Joh84] and Fox et al. [FJL+88]. Algorithm 9.1 is adopted from [FJL+88]. The shuffled row-major indexing formulation of bitonic sort on a mesh-connected computer is presented by Thompson and Kung [TK77]. They also show how the odd-even merge sort can be used with snakelike row-major indexing. Nassimi and Sahni [NS79] present a row-major indexed bitonic sort formulation for a mesh with the same performance as shuffled row-major indexing. An improved version of the mesh odd-even merge is proposed by Kumar and Hirschberg [KH83]. The compare-split operation can be implemented in many ways. Baudet and Stevenson [BS78] describe one way to perform this operation. An alternative way of performing a compare-split operation based on a bitonic sort (Problem 9.1) that requires no additional memory was discovered by Hsiao and Menon [HM80].
The odd-even transposition sort is described by Knuth [Knu73]. Several early references to parallel sorting by odd-even transposition are given by Knuth [Knu73] and Kung [Kun80]. The block-based extension of the algorithm is due to Baudet and Stevenson [BS78]. Another variation of block-based odd-even transposition sort that uses bitonic merge-split is described by DeWitt, Friedland, Hsiao, and Menon [DFHM82]. Their algorithm uses p processes and runs in time O (n + n log(n/p)). In contrast to the algorithm of Baudet and Stevenson [BS78], which is faster but requires 4n/p storage locations in each process, the algorithm of DeWitt et al. requires only (n/p) + 1 storage locations to perform the compare-split operation.
The shellsort algorithm described in Section 9.3.2 is due to Fox et al. [FJL+88]. They show that, as n increases, the probability that the final odd-even transposition will exhibit worst-case performance (in other words, will require p phases) diminishes. A different shellsort algorithm based on the original sequential algorithm [She59] is described by Quinn [Qui88].
The sequential quicksort algorithm is due to Hoare [Hoa62]. Sedgewick [Sed78] provides a good reference on the details of the implementation and how they affect its performance. The random pivot-selection scheme is described and analyzed by Robin [Rob75]. The algorithm for sequence partitioning on a single process was suggested by Sedgewick [Sed78] and used in parallel formulations by Raskin [Ras78], Deminet [Dem82], and Quinn [Qui88]. The CRCW PRAM algorithm (Section 9.4.2) is due to Chlebus and Vrto [CV91]. Many other quicksort-based algorithms for PRAM and shared-address-space parallel computers have been developed that can sort n elements in time Θ(log n) by using Θ(n) processes. Martel and Gusfield [MG89] developed a quicksort algorithm for a CRCW PRAM that requires space O (n3) on the average. An algorithm suited to shared-address-space parallel computers with fetch-and-add capabilities was discovered by Heidelberger, Norton, and Robinson [HNR90]. Their algorithm runs in time Θ(log n) on the average and can be adapted for commercially available shared-address-space computers. The hypercube formulation of quicksort described in Problem 9.17 is due to Wagar [Wag87]. His hyperquicksort algorithm uses the median-based pivot-selection scheme and assumes that the elements in each process have the same distribution. His experimental results show that hyperquicksort is faster than bitonic sort on a hypercube. An alternate pivot-selection scheme (Problem 9.20) was implemented by Fox et al. [FJL+88]. This scheme significantly improves the performance of hyperquicksort when the elements are not evenly distributed in each process. Plaxton [Pla89] describes a quicksort algorithm on a p-process hypercube that sorts n elements in time O ((n log n)/p +(n log3/2 p)/p +log3 p log(n/p)). This algorithm uses a time O ((n/p) log log p + log2 p log(n/p)) parallel selection algorithm to determine the perfect pivot selection. The mesh formulation of quicksort (Problem 9.24) is due to Singh, Kumar, Agha, and Tomlinson [SKAT91a]. They also describe a modification to the algorithm that reduces the complexity of each step by a factor of Θ(log p).
The sequential bucket sort algorithm was first proposed by Isaac and Singleton in 1956. Hirschberg [Hir78] proposed a bucket sort algorithm for the EREW PRAM model. This algorithm sorts n elements in the range [0...n − 1] in time Θ(log n) by using n processes. A side effect of this algorithm is that duplicate elements are eliminated. Their algorithm requires space Θ(n2). Hirschberg [Hir78] generalizes this algorithm so that duplicate elements remain in the sorted array. The generalized algorithm sorts n elements in time Θ(k log n) by using n1+1/k processes, where k is an arbitrary integer.
The sequential sample sort algorithm was discovered by Frazer and McKellar [FM70]. The parallel sample sort algorithm (Section 9.5) was discovered by Shi and Schaeffer [SS90]. Several parallel formulations of sample sort for different parallel architectures have been proposed. Abali, Ozguner, and Bataineh [AOB93] presented a splitter selection scheme that guarantees that the number of elements ending up in each bucket is n/p. Their algorithm requires time O ((n log n)/p + p log2 n), on average, to sort n elements on a p-process hypercube. Reif and Valiant [RV87] present a sample sort algorithm that sorts n elements on an n-process hypercube-connected computer in time O (log n) with high probability. Won and Sahni [WS88] and Seidel and George [SG88] present parallel formulations of a variation of sample sort called bin sort [FKO86].
Many other parallel sorting algorithms have been proposed. Various parallel sorting algorithms can be efficiently implemented on a PRAM model or on shared-address-space computers. Akl [Akl85], Borodin and Hopcroft [BH82], Shiloach and Vishkin [SV81], and Bitton, DeWitt, Hsiao, and Menon [BDHM84] provide a good survey of the subject. Valiant [Val75] proposed a sorting algorithm for a shared-address-space SIMD computer that sorts by merging. It sorts n elements in time O (log n log log n) by using n/2 processes. Reischuk [Rei81] was the first to develop an algorithm that sorted n elements in time Θ(log n) for an n-process PRAM. Cole [Col88] developed a parallel merge-sort algorithm that sorts n elements in time Θ(log n) on an EREW PRAM. Natvig [Nat90] has shown that the constants hidden behind the asymptotic notation are very large. In fact, the Θ(log2 n) bitonic sort outperforms the Θ(log n) merge sort as long as n is smaller than 7.6 × 1022! Plaxton [Pla89] has developed a hypercube sorting algorithm, called smoothsort, that runs asymptotically faster than any previously known algorithm for that architecture. Leighton [Lei85a] proposed a sorting algorithm, called columnsort, that consists of a sequence of sorts followed by elementary matrix operations. Columnsort is a generalization of Batcher’s odd-even sort. Nigam and Sahni [NS93] presented an algorithm based on Leighton’s columnsort for reconfigurable meshes with buses that sorts n elements on an n2-process mesh in time O (1).
9.1 Consider the following technique for performing the compare-split operation. Let x1, x2, ..., xk be the elements stored at process Pi in increasing order, and let y1, y2, ..., yk be the elements stored at process Pj in decreasing order. Process Pi sends x1 to Pj. Process Pj compares x1 with y1 and then sends the larger element back to process Pi and keeps the smaller element for itself. The same procedure is repeated for pairs (x2, y2), (x3, y3), ..., (xk , yk ). If for any pair (xl , yl ) for 1 ≤ l ≤ k, xl ≥ yl, then no more exchanges are needed. Finally, each process sorts its elements. Show that this method correctly performs a compare-split operation. Analyze its run time, and compare the relative merits of this method to those of the method presented in the text. Is this method better suited for MIMD or SIMD parallel computers?
9.2 Show that the ≤ relation, as defined in Section 9.1 for blocks of elements, is a partial ordering relation.
Hint: A relation is a partial ordering if it is reflexive, antisymmetric, and transitive.
9.3 Consider the sequence s = {a0, a1, ..., an−1},where n is a power of 2. In the following cases, prove that the sequences s1 and s2 obtained by performing the bitonic split operation described in Section 9.2.1, on the sequence s, satisfy the properties that (1) s1 and s2 are bitonic sequences, and (2) the elements of s1 are smaller than the elements of s2:
s is a bitonic sequence such that a0 ≤ a1 ≤ ··· ≤ an/2−1 and an/2 ≥ an/2+1 ≥ ··· ≥ an−1.
s is a bitonic sequence such that a0 ≤ a1 ≤ ··· ≤ ai and ai +1 ≥ ai +2 ≥ ··· ≥ an−1 for some i, 0 ≤ i ≤ n − 1.
s is a bitonic sequence that becomes increasing-decreasing after shifting its elements.
9.4 In the parallel formulations of bitonic sort, we assumed that we had n processes available to sort n items. Show how the algorithm needs to be modified when only n/2 processes are available.
9.5 Show that, in the hypercube formulation of bitonic sort, each bitonic merge of sequences of size 2k is performed on a k-dimensional hypercube and each sequence is assigned to a separate hypercube.
9.6 Show that the parallel formulation of bitonic sort shown in Algorithm 9.1 is correct. In particular, show that the algorithm correctly compare-exchanges elements and that the elements end up in the appropriate processes.
9.7 Consider the parallel formulation of bitonic sort for a mesh-connected parallel computer. Compute the exact parallel run time of the following formulations:
One that uses the row-major mapping shown in Figure 9.11(a) for a mesh with store-and-forward routing.
One that uses the row-major snakelike mapping shown in Figure 9.11(b) for a mesh with store-and-forward routing.
One that uses the row-major shuffled mapping shown in Figure 9.11(c) for a mesh with store-and-forward routing.
Also, determine how the above run times change when cut-through routing is used.
9.8 Show that the block-based bitonic sort algorithm that uses compare-split operations is correct.
9.9 Consider a ring-connected parallel computer with n processes. Show how to map the input wires of the bitonic sorting network onto the ring so that the communication cost is minimized. Analyze the performance of your mapping. Consider the case in which only p processes are available. Analyze the performance of your parallel formulation for this case. What is the largest number of processes that can be used while maintaining a cost-optimal parallel formulation? What is the isoefficiency function of your scheme?
9.10 Prove that the block-based odd-even transposition sort yields a correct algorithm.
Hint: This problem is similar to Problem 9.8.
9.11 Show how to apply the idea of the shellsort algorithm (Section 9.3.2) to a p-process mesh-connected computer. Your algorithm does not need to be an exact copy of the hypercube formulation.
9.12 Show how to parallelize the sequential shellsort algorithm for a p-process hypercube. Note that the shellsort algorithm presented in Section 9.3.2 is not an exact parallelization of the sequential algorithm.
9.13 Consider the shellsort algorithm presented in Section 9.3.2. Its performance depends on the value of l, which is the number of odd and even phases performed during the second phase of the algorithm. Describe a worst-case initial key distribution that will require l = Θ(p) phases. What is the probability of this worst-case scenario?
9.14 In Section 9.4.1 we discussed a parallel formulation of quicksort for a CREW PRAM that is based on assigning each subproblem to a separate process. This formulation uses n processes to sort n elements. Based on this approach, derive a parallel formulation that uses p processes, where (p < n). Derive expressions for the parallel run time, efficiency, and isoefficiency function. What is the maximum number of processes that your parallel formulation can use and still remain cost-optimal?
9.15 Derive an algorithm that traverses the binary search tree constructed by the algorithm in Algorithm 9.6 and determines the position of each element in the sorted array. Your algorithm should use n processes and solve the problem in time Θ(log n) on an arbitrary CRCW PRAM.
9.16 Consider the PRAM formulation of the quicksort algorithm (Section 9.4.2). Compute the average height of the binary tree generated by the algorithm.
9.17 Consider the following parallel quicksort algorithm that takes advantage of the topology of a p-process hypercube connected parallel computer. Let n be the number of elements to be sorted and p = 2d be the number of processes in a d-dimensional hypercube. Each process is assigned a block of n/p elements, and the labels of the processes define the global order of the sorted sequence. The algorithm starts by selecting a pivot element, which is broadcast to all processes. Each process, upon receiving the pivot, partitions its local elements into two blocks, one with elements smaller than the pivot and one with elements larger than the pivot. Then the processes connected along the dth communication link exchange appropriate blocks so that one retains elements smaller than the pivot and the other retains elements larger than the pivot. Specifically, each process with a 0 in the dth bit (the most significant bit) position of the binary representation of its process label retains the smaller elements, and each process with a 1 in the dth bit retains the larger elements. After this step, each process in the (d − 1)-dimensional hypercube whose dth label bit is 0 will have elements smaller than the pivot, and each process in the other (d − 1)-dimensional hypercube will have elements larger than the pivot. This procedure is performed recursively in each subcube, splitting the subsequences further. After d such splits – one along each dimension – the sequence is sorted with respect to the global ordering imposed on the processes. This does not mean that the elements at each process are sorted. Therefore, each process sorts its local elements by using sequential quicksort. This hypercube formulation of quicksort is shown in Algorithm 9.9. The execution of the algorithm is illustrated in Figure 9.21.
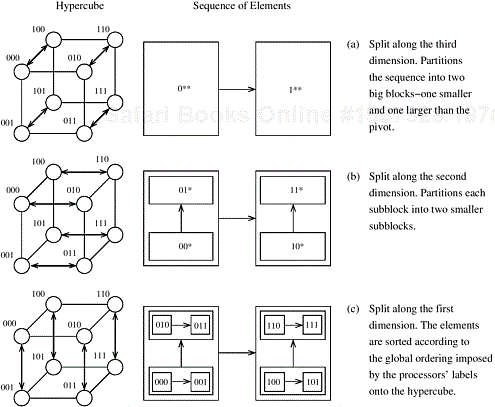
Figure 9.21. The execution of the hypercube formulation of quicksort for d = 3. The three splits – one along each communication link – are shown in (a), (b), and (c). The second column represents the partitioning of the n-element sequence into subcubes. The arrows between subcubes indicate the movement of larger elements. Each box is marked by the binary representation of the process labels in that subcube. A ∗ denotes that all the binary combinations are included.
Example 9.9. A parallel formulation of quicksort on a d-dimensional hypercube. B is the n/p-element subsequence assigned to each process.
1. procedure HYPERCUBE_QUICKSORT (B, n) 2. begin 3. id := process’s label; 4. for i := 1 to d do 5. begin 6. x := pivot; 7. partition B into B1 and B2 such that B1 ≤ x < B2; 8. if ith bit is 0 then 9. begin 10. send B2 to the process along the i th communication link; 11. C := subsequence received along the i th communication link; 12. B := B1 ∪ C ; 13. endif 14. else 15. send B1 to the process along the ith communication link; 16. C := subsequence received along the ith communication link; 17. B := B2 ∪ C ; 18. endelse 19. endfor 20. sort B using sequential quicksort; 21. end HYPERCUBE_QUICKSORT
Analyze the complexity of this hypercube-based parallel quicksort algorithm. Derive expressions for the parallel runtime, speedup, and efficiency. Perform this analysis assuming that the elements that were initially assigned at each process are distributed uniformly.
9.18 Consider the parallel formulation of quicksort for a d-dimensional hypercube described in Problem 9.17. Show that after d splits – one along each communication link – the elements are sorted according to the global order defined by the process’s labels.
9.19 Consider the parallel formulation of quicksort for a d-dimensional hypercube described in Problem 9.17. Compare this algorithm against the message-passing quicksort algorithm described in Section 9.4.3. Which algorithm is more scalable? Which algorithm is more sensitive on poor selection of pivot elements?
9.20 An alternative way of selecting pivots in the parallel formulation of quicksort for a d-dimensional hypercube (Problem 9.17) is to select all the 2d − 1 pivots at once as follows:
Each process picks a sample of l elements at random.
All processes together sort the sample of l × 2d items by using the shellsort algorithm (Section 9.3.2).
Choose 2d − 1 equally distanced pivots from this list.
Broadcast pivots so that all the processes know the pivots.
How does the quality of this pivot selection scheme depend on l? Do you think l should be a function of n? Under what assumptions will this scheme select good pivots? Do you think this scheme works when the elements are not identically distributed on each process? Analyze the complexity of this scheme.
9.21 Another pivot selection scheme for parallel quicksort for hypercube (Section 9.17) is as follows. During the split along the ith dimension, 2i −1 pairs of processes exchange elements. The pivot is selected in two steps. In the first step, each of the 2i −1 pairs of processes compute the median of their combined sequences. In the second step, the median of the 2i −1 medians is computed. This median of medians becomes the pivot for the split along the ith communication link. Subsequent pivots are selected in the same way among the participating subcubes. Under what assumptions will this scheme yield good pivot selections? Is this better than the median scheme described in the text? Analyze the complexity of selecting the pivot.
Hint: If A and B are two sorted sequences, each having n elements, then we can find the median of A ∪ B in time Θ(log n).
9.22 In the parallel formulation of the quicksort algorithm on shared-address-space and message-passing architectures (Section 9.4.3) each iteration is followed by a barrier synchronization. Is barrier synchronization necessary to ensure the correctness of the algorithm? If not, then how does the performance change in the absence of barrier synchronization?
9.23 Consider the message-passing formulation of the quicksort algorithm presented in Section 9.4.3. Compute the exact (that is, using ts, tw, and tc) parallel run time and efficiency of the algorithm under the assumption of perfect pivots. Compute the various components of the isoefficiency function of your formulation when
tc = 1, tw = 1, ts = 1
tc = 1, tw = 1, ts = 10
tc = 1, tw = 10, ts = 100
for cases in which the desired efficiency is 0.50, 0.75, and 0.95. Does the scalability of this formulation depend on the desired efficiency and the architectural characteristics of the machine?
9.24 Consider the following parallel formulation of quicksort for a mesh-connected message-passing parallel computer. Assume that one element is assigned to each process. The recursive partitioning step consists of selecting the pivot and then rearranging the elements in the mesh so that those smaller than the pivot are in one part of the mesh and those larger than the pivot are in the other. We assume that the processes in the mesh are numbered in row-major order. At the end of the quicksort algorithm, elements are sorted with respect to this order. Consider the partitioning step for an arbitrary subsequence illustrated in Figure 9.22(a). Let k be the length of this sequence, and let Pm, Pm+1, ..., Pm+k be the mesh processes storing it. Partitioning consists of the following four steps:
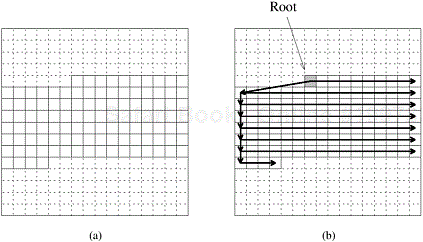
Figure 9.22. (a) An arbitrary portion of a mesh that holds part of the sequence to be sorted at some point during the execution of quicksort, and (b) a binary tree embedded into the same portion of the mesh.
A pivot is selected at random and sent to process Pm. Process Pm broadcasts this pivot to all k processes by using an embedded tree, as shown in Figure 9.22(b). The root (Pm) transmits the pivot toward the leaves. The tree embedding is also used in the following steps.
Information is gathered at each process and passed up the tree. In particular, each process counts the number of elements smaller and larger than the pivot in both its left and right subtrees. Each process knows the pivot value and therefore can determine if its element is smaller or larger. Each process propagates two values to its parent: the number of elements smaller than the pivot and the number of elements larger than the pivot in the process’s subtree. Because the tree embedded in the mesh is not complete, some nodes will not have left or right subtrees. At the end of this step, process Pm knows how many of the k elements are smaller and larger than the pivot. If s is the number of the elements smaller than the pivot, then the position of the pivot in the sorted sequence is Pm+s.
Information is propagated down the tree to enable each element to be moved to its proper position in the smaller or larger partitions. Each process in the tree receives from its parent the next empty position in the smaller and larger partitions. Depending on whether the element stored at each process is smaller or larger than the pivot, the process propagates the proper information down to its subtrees. Initially, the position for elements smaller than the pivot is Pm and the position for elements larger than the pivot is Pm+s+1.
The processes perform a permutation, and each element moves to the proper position in the smaller or larger partition.
This algorithm is illustrated in Figure 9.23.
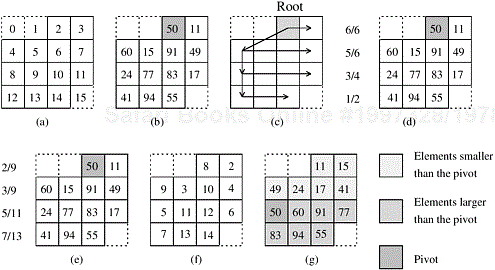
Figure 9.23. Partitioning a sequence of 13 elements on a 4 × 4 mesh: (a) row-major numbering of the mesh processes, (b) the elements stored in each process (the shaded element is the pivot), (c) the tree embedded on a portion of the mesh, (d) the number of smaller or larger elements in the process of the first column after the execution of the second step, (e) the destination of the smaller or larger elements propagated down to the processes in the first column during the third step, (f) the destination of the elements at the end of the third step, and (g) the locations of the elements after one-to-one personalized communication.
Analyze the complexity of this mesh-based parallel quicksort algorithm. Derive expressions for the parallel runtime, speedup, and efficiency. Perform this analysis assuming that the elements that were initially assigned at each process are distributed uniformly.
9.25 Consider the quicksort formulation for a mesh described in Problem 9.24. Describe a scaled-down formulation that uses p < n processes. Analyze its parallel run time, speedup, and isoefficiency function.
9.26 Consider the enumeration sort algorithm presented in Section 9.6.1. Show how the algorithm can be implemented on each of the following:
a CREW PRAM
a EREW PRAM
a hypercube-connected parallel computer
a mesh-connected parallel computer.
Analyze the performance of your formulations. Furthermore, show how you can extend this enumeration sort to a hypercube to sort n elements using p processes.
9.27 Derive expressions for the speedup, efficiency, and isoefficiency function of the bucket sort parallel formulation presented in Section 9.5. Compare these expressions with the expressions for the other sorting algorithms presented in this chapter. Which parallel formulations perform better than bucket sort, and which perform worse?
9.28 Show that the splitter selection scheme described in Section 9.5 guarantees that the number of elements in each of the m buckets is less than 2n/m.
9.29 Derive expressions for the speedup, efficiency, and isoefficiency function of the sample sort parallel formulation presented in Section 9.5. Derive these metrics under each of the following conditions: (1) the p sub-blocks at each process are of equal size, and (2) the size of the p sub-blocks at each process can vary by a factor of log p.
9.30 In the sample sort algorithm presented in Section 9.5, all processes send p − 1 elements to process P0, which sorts the p(p − 1) elements and distributes splitters to all the processes. Modify the algorithm so that the processes sort the p(p − 1) elements in parallel using bitonic sort. How will you choose the splitters? Compute the parallel run time, speedup, and efficiency of your formulation.
9.31 How does the performance of radix sort (Section 9.6.2) depend on the value of r? Compute the value of r that minimizes the run time of the algorithm.
9.32 Extend the radix sort algorithm presented in Section 9.6.2 to the case in which p processes (p < n) are used to sort n elements. Derive expressions for the speedup, efficiency, and isoefficiency function for this parallel formulation. Can you devise a better ranking mechanism?