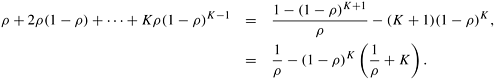Search algorithms can be used to solve discrete optimization problems (DOPs), a class of computationally expensive problems with significant theoretical and practical interest. Search algorithms solve DOPs by evaluating candidate solutions from a finite or countably infinite set of possible solutions to find one that satisfies a problem-specific criterion. DOPs are also referred to as combinatorial problems.
A discrete optimization problem can be expressed as a tuple (S, f). The set S is a finite or countably infinite set of all solutions that satisfy specified constraints. This set is called the set of feasible solutions. The function f is the cost function that maps each element in set S onto the set of real numbers R.
The objective of a DOP is to find a feasible solution xopt, such that f (xopt) ≤ f (x) for all x ∊ S.
Problems from various domains can be formulated as DOPs. Some examples are planning and scheduling, the optimal layout of VLSI chips, robot motion planning, test-pattern generation for digital circuits, and logistics and control.
Example 11.1 The 0/1 integer-linear-programming problem
In the 0/1 integer-linear-programming problem, we are given an m × n matrix A, an m × 1 vector b, and an n × 1 vector c. The objective is to determine an n × 1 vector x![]() whose elements can take on only the value 0 or 1. The vector must satisfy the constraint
whose elements can take on only the value 0 or 1. The vector must satisfy the constraint
and the function
must be minimized. For this problem, the set S is the set of all values of the vector x![]() that satisfy the equation Ax
that satisfy the equation Ax![]() ≥ b. ▪
≥ b. ▪
Example 11.2 The 8-puzzle problem
The 8-puzzle problem consists of a 3 × 3 grid containing eight tiles, numbered one through eight. One of the grid segments (called the “blank”) is empty. A tile can be moved into the blank position from a position adjacent to it, thus creating a blank in the tile’s original position. Depending on the configuration of the grid, up to four moves are possible: up, down, left, and right. The initial and final configurations of the tiles are specified. The objective is to determine a shortest sequence of moves that transforms the initial configuration to the final configuration. Figure 11.1 illustrates sample initial and final configurations and a sequence of moves leading from the initial configuration to the final configuration.
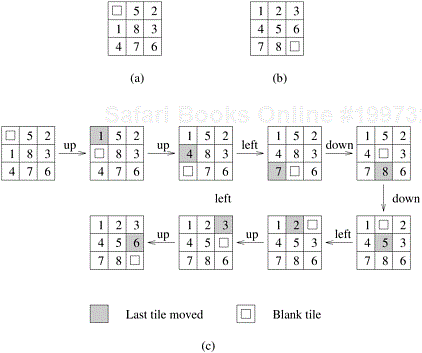
Figure 11.1. An 8-puzzle problem instance: (a) initial configuration; (b) final configuration; and (c) a sequence of moves leading from the initial to the final configuration.
The set S for this problem is the set of all sequences of moves that lead from the initial to the final configurations. The cost function f of an element in S is defined as the number of moves in the sequence. ▪
In most problems of practical interest, the solution set S is quite large. Consequently, it is not feasible to exhaustively enumerate the elements in S to determine the optimal element xopt. Instead, a DOP can be reformulated as the problem of finding a minimum-cost path in a graph from a designated initial node to one of several possible goal nodes. Each element x in S can be viewed as a path from the initial node to one of the goal nodes. There is a cost associated with each edge of the graph, and a cost function f is defined in terms of these edge costs. For many problems, the cost of a path is the sum of the edge costs. Such a graph is called a state space, and the nodes of the graph are called states. A terminal node is one that has no successors. All other nodes are called nonterminal nodes. The 8-puzzle problem can be naturally formulated as a graph search problem. In particular, the initial configuration is the initial node, and the final configuration is the goal node. Example 11.3 illustrates the process of reformulating the 0/1 integer-linear-programming problem as a graph search problem.
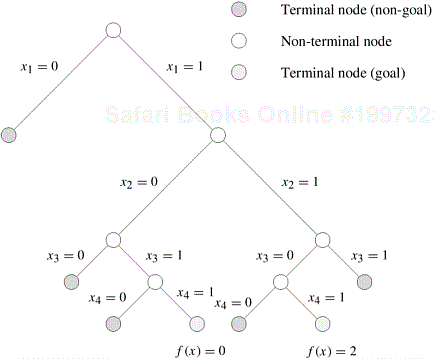
Example 11.3 The 0/1 integer-linear-programming problem revisited
Consider an instance of the 0/1 integer-linear-programming problem defined in Example 11.1. Let the values of A, b, and c be given by

The constraints corresponding to A, b, and c are as follows:

and the function f (x) to be minimized is
Each of the four elements of vector x can take the value 0 or 1. There are 24 = 16 possible values for x. However, many of these values do not satisfy the problem’s constraints.
The problem can be reformulated as a graph-search problem. The initial node represents the state in which none of the elements of vector x have been assigned values. In this example, we assign values to vector elements in subscript order; that is, first x1, then x2, and so on. The initial node generates two nodes corresponding to x1 = 0 and x1 = 1. After a variable xi has been assigned a value, it is called a fixed variable. All variables that are not fixed are called free variables.
After instantiating a variable to 0 or 1, it is possible to check whether an instantiation of the remaining free variables can lead to a feasible solution. We do this by using the following condition:
The left side of Equation 11.1 is the maximum value of ![]() that can be obtained by instantiating the free variables to either 0 or 1. If this value is greater than or equal to bi , for i = 1, 2,..., m, then the node may lead to a feasible solution.
that can be obtained by instantiating the free variables to either 0 or 1. If this value is greater than or equal to bi , for i = 1, 2,..., m, then the node may lead to a feasible solution.
For each of the nodes corresponding to x1 = 0 and x1 = 1, the next variable (x2) is selected and assigned a value. The nodes are then checked for feasibility. This process continues until all the variables have been assigned and the feasible set has been generated. Figure 11.2 illustrates this process.
Function f (x) is evaluated for each of the feasible solutions; the solution with the minimum value is the desired solution. Note that it is unnecessary to generate the entire feasible set to determine the solution. Several search algorithms can determine an optimal solution by searching only a portion of the graph. ▪
For some problems, it is possible to estimate the cost to reach the goal state from an intermediate state. This cost is called a heuristic estimate. Let h(x) denote the heuristic estimate of reaching the goal state from state x and g(x) denote the cost of reaching state x from initial state s along the current path. The function h is called a heuristic function. If h(x) is a lower bound on the cost of reaching the goal state from state x for all x, then h is called admissible. We define function l(x) as the sum h(x) + g(x). If h is admissible, then l(x) is a lower bound on the cost of the path to a goal state that can be obtained by extending the current path between s and x. In subsequent examples we will see how an admissible heuristic can be used to determine the least-cost sequence of moves from the initial state to a goal state.
Example 11.4 An admissible heuristic function for the 8-puzzle
Assume that each position in the 8-puzzle grid is represented as a pair. The pair (1, 1) represents the top-left grid position and the pair (3, 3) represents the bottom-right position. The distance between positions (i, j) and (k, l) is defined as |i − k| + | j − l|. This distance is called the Manhattan distance. The sum of the Manhattan distances between the initial and final positions of all tiles is an estimate of the number of moves required to transform the current configuration into the final configuration. This estimate is called the Manhattan heuristic. Note that if h(x) is the Manhattan distance between configuration x and the final configuration, then h(x) is also a lower bound on the number of moves from configuration x to the final configuration. Hence the Manhattan heuristic is admissible. ▪
Once a DOP has been formulated as a graph search problem, it can be solved by algorithms such as branch-and-bound search and heuristic search. These techniques use heuristics and the structure of the search space to solve DOPs without searching the set S exhaustively.
DOPs belong to the class of NP-hard problems. One may argue that it is pointless to apply parallel processing to these problems, since we can never reduce their worst-case run time to a polynomial without using exponentially many processors. However, the average-time complexity of heuristic search algorithms for many problems is polynomial. Furthermore, there are heuristic search algorithms that find suboptimal solutions for specific problems in polynomial time. In such cases, bigger problem instances can be solved using parallel computers. Many DOPs (such as robot motion planning, speech understanding, and task scheduling) require real-time solutions. For these applications, parallel processing may be the only way to obtain acceptable performance. Other problems, for which optimal solutions are highly desirable, can be solved for moderate-sized instances in a reasonable amount of time by using parallel search techniques (for example, VLSI floor-plan optimization, and computer-aided design).
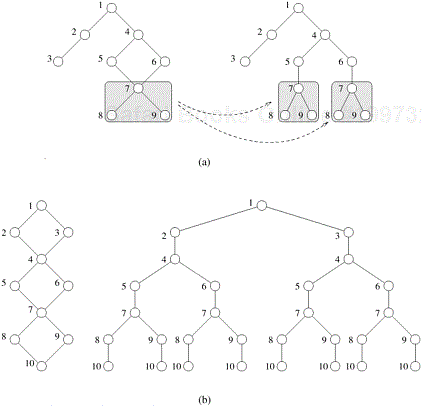
The most suitable sequential search algorithm to apply to a state space depends on whether the space forms a graph or a tree. In a tree, each new successor leads to an unexplored part of the search space. An example of this is the 0/1 integer-programming problem. In a graph, however, a state can be reached along multiple paths. An example of such a problem is the 8-puzzle. For such problems, whenever a state is generated, it is necessary to check if the state has already been generated. If this check is not performed, then effectively the search graph is unfolded into a tree in which a state is repeated for every path that leads to it (Figure 11.3).
For many problems (for example, the 8-puzzle), unfolding increases the size of the search space by a small factor. For some problems, however, unfolded graphs are much larger than the original graphs. Figure 11.3(b) illustrates a graph whose corresponding tree has an exponentially higher number of states. In this section, we present an overview of various sequential algorithms used to solve DOPs that are formulated as tree or graph search problems.
Depth-first search (DFS) algorithms solve DOPs that can be formulated as tree-search problems. DFS begins by expanding the initial node and generating its successors. In each subsequent step, DFS expands one of the most recently generated nodes. If this node has no successors (or cannot lead to any solutions), then DFS backtracks and expands a different node. In some DFS algorithms, successors of a node are expanded in an order determined by their heuristic values. A major advantage of DFS is that its storage requirement is linear in the depth of the state space being searched. The following sections discuss three algorithms based on depth-first search.
Simple backtracking is a depth-first search method that terminates upon finding the first solution. Thus, it is not guaranteed to find a minimum-cost solution. Simple backtracking uses no heuristic information to order the successors of an expanded node. A variant, ordered backtracking, does use heuristics to order the successors of an expanded node.
Depth-first branch-and-bound (DFBB) exhaustively searches the state space; that is, it continues to search even after finding a solution path. Whenever it finds a new solution path, it updates the current best solution path. DFBB discards inferior partial solution paths (that is, partial solution paths whose extensions are guaranteed to be worse than the current best solution path). Upon termination, the current best solution is a globally optimal solution.
Trees corresponding to DOPs can be very deep. Thus, a DFS algorithm may get stuck searching a deep part of the search space when a solution exists higher up on another branch. For such trees, we impose a bound on the depth to which the DFS algorithm searches. If the node to be expanded is beyond the depth bound, then the node is not expanded and the algorithm backtracks. If a solution is not found, then the entire state space is searched again using a larger depth bound. This technique is called iterative deepening depth-first search (ID-DFS). Note that this method is guaranteed to find a solution path with the fewest edges. However, it is not guaranteed to find a least-cost path.
Iterative deepening A* (IDA*) is a variant of ID-DFS. IDA* uses the l-values of nodes to bound depth (recall from Section 11.1 that for node x, l(x) = g(x) + h(x)). IDA* repeatedly performs cost-bounded DFS over the search space. In each iteration, IDA* expands nodes depth-first. If the l-value of the node to be expanded is greater than the cost bound, then IDA* backtracks. If a solution is not found within the current cost bound, then IDA* repeats the entire depth-first search using a higher cost bound. In the first iteration, the cost bound is set to the l-value of the initial state s. Note that since g(s) is zero, l(s) is equal to h(s). In each subsequent iteration, the cost bound is increased. The new cost bound is equal to the minimum l-value of the nodes that were generated but could not be expanded in the previous iteration. The algorithm terminates when a goal node is expanded. IDA* is guaranteed to find an optimal solution if the heuristic function is admissible. It may appear that IDA* performs a lot of redundant work across iterations. However, for many problems the redundant work performed by IDA* is minimal, because most of the work is done deep in the search space.
Example 11.5 Depth-first search: the 8-puzzle
Figure 11.4 shows the execution of depth-first search for solving the 8-puzzle problem. The search starts at the initial configuration. Successors of this state are generated by applying possible moves. During each step of the search algorithm a new state is selected, and its successors are generated. The DFS algorithm expands the deepest node in the tree. In step 1, the initial state A generates states B and C. One of these is selected according to a predetermined criterion. In the example, we order successors by applicable moves as follows: up, down, left, and right. In step 2, the DFS algorithm selects state B and generates states D, E, and F. Note that the state D can be discarded, as it is a duplicate of the parent of B. In step 3, state E is expanded to generate states G and H. Again G can be discarded because it is a duplicate of B. The search proceeds in this way until the algorithm backtracks or the final configuration is generated. ▪
In each step of the DFS algorithm, untried alternatives must be stored. For example, in the 8-puzzle problem, up to three untried alternatives are stored at each step. In general, if m is the amount of storage required to store a state, and d is the maximum depth, then the total space requirement of the DFS algorithm is O (md). The state-space tree searched by parallel DFS can be efficiently represented as a stack. Since the depth of the stack increases linearly with the depth of the tree, the memory requirements of a stack representation are low.
There are two ways of storing untried alternatives using a stack. In the first representation, untried alternates are pushed on the stack at each step. The ancestors of a state are not represented on the stack. Figure 11.5(b) illustrates this representation for the tree shown in Figure 11.5(a). In the second representation, shown in Figure 11.5(c), untried alternatives are stored along with their parent state. It is necessary to use the second representation if the sequence of transformations from the initial state to the goal state is required as a part of the solution. Furthermore, if the state space is a graph in which it is possible to generate an ancestor state by applying a sequence of transformations to the current state, then it is desirable to use the second representation, because it allows us to check for duplication of ancestor states and thus remove any cycles from the state-space graph. The second representation is useful for problems such as the 8-puzzle. In Example 11.5, using the second representation allows the algorithm to detect that nodes D and G should be discarded.
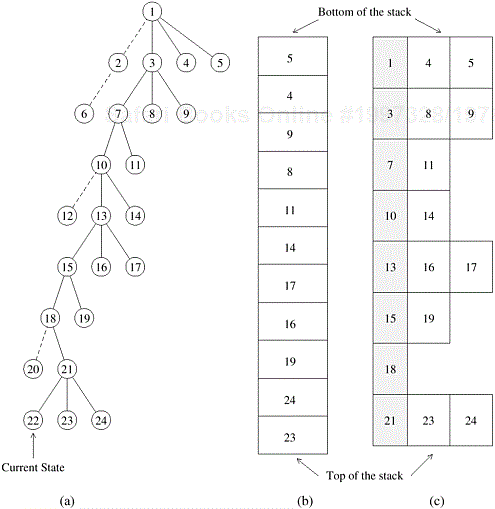
Figure 11.5. Representing a DFS tree: (a) the DFS tree; successor nodes shown with dashed lines have already been explored; (b) the stack storing untried alternatives only; and (c) the stack storing untried alternatives along with their parent. The shaded blocks represent the parent state and the block to the right represents successor states that have not been explored.
Best-first search (BFS) algorithms can search both graphs and trees. These algorithms use heuristics to direct the search to portions of the search space likely to yield solutions. Smaller heuristic values are assigned to more promising nodes. BFS maintains two lists: open and closed. At the beginning, the initial node is placed on the open list. This list is sorted according to a heuristic evaluation function that measures how likely each node is to yield a solution. In each step of the search, the most promising node from the open list is removed. If this node is a goal node, then the algorithm terminates. Otherwise, the node is expanded. The expanded node is placed on the closed list. The successors of the newly expanded node are placed on the open list under one of the following circumstances: (1) the successor is not already on the open or closed lists, and (2) the successor is already on the open or closed list but has a lower heuristic value. In the second case, the node with the higher heuristic value is deleted.
A common BFS technique is the A* algorithm. The A* algorithm uses the lower bound function l as a heuristic evaluation function. Recall from Section 11.1 that for each node x , l(x) is the sum of g(x) and h(x). Nodes in the open list are ordered according to the value of the l function. At each step, the node with the smallest l-value (that is, the best node) is removed from the open list and expanded. Its successors are inserted into the open list at the proper positions and the node itself is inserted into the closed list. For an admissible heuristic function, A* finds an optimal solution.
The main drawback of any BFS algorithm is that its memory requirement is linear in the size of the search space explored. For many problems, the size of the search space is exponential in the depth of the tree expanded. For problems with large search spaces, memory becomes a limitation.
Example 11.6 Best-first search: the 8-puzzle
Consider the 8-puzzle problem from Examples 11.2 and 11.4. Figure 11.6 illustrates four steps of best-first search on the 8-puzzle. At each step, a state x with the minimum l-value (l(x) = g(x) + h(x)) is selected for expansion. Ties are broken arbitrarily. BFS can check for a duplicate nodes, since all previously generated nodes are kept on either the open or closed list. ▪
Parallel search algorithms incur overhead from several sources. These include communication overhead, idle time due to load imbalance, and contention for shared data structures. Thus, if both the sequential and parallel formulations of an algorithm do the same amount of work, the speedup of parallel search on p processors is less than p. However, the amount of work done by a parallel formulation is often different from that done by the corresponding sequential formulation because they may explore different parts of the search space.
Let W be the amount of work done by a single processor, and Wp be the total amount of work done by p processors. The search overhead factor of the parallel system is defined as the ratio of the work done by the parallel formulation to that done by the sequential formulation, or Wp/W. Thus, the upper bound on speedup for the parallel system is given by p ×(W/Wp). The actual speedup, however, may be less due to other parallel processing overhead. In most parallel search algorithms, the search overhead factor is greater than one. However, in some cases, it may be less than one, leading to superlinear speedup. If the search overhead factor is less than one on the average, then it indicates that the serial search algorithm is not the fastest algorithm for solving the problem.
To simplify our presentation and analysis, we assume that the time to expand each node is the same, and W and Wp are the number of nodes expanded by the serial and the parallel formulations, respectively. If the time for each expansion is tc, then the sequential run time is given by TS = tcW. In the remainder of the chapter, we assume that tc = 1. Hence, the problem size W and the serial run time TS become the same.
We start our discussion of parallel depth-first search by focusing on simple backtracking. Parallel formulations of depth-first branch-and-bound and IDA* are similar to those discussed in this section and are addressed in Sections 11.4.6 and 11.4.7.
The critical issue in parallel depth-first search algorithms is the distribution of the search space among the processors. Consider the tree shown in Figure 11.7. Note that the left subtree (rooted at node A) can be searched in parallel with the right subtree (rooted at node B). By statically assigning a node in the tree to a processor, it is possible to expand the whole subtree rooted at that node without communicating with another processor. Thus, it seems that such a static allocation yields a good parallel search algorithm.
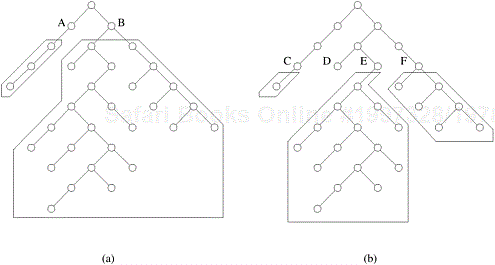
Figure 11.7. The unstructured nature of tree search and the imbalance resulting from static partitioning.
Let us see what happens if we try to apply this approach to the tree in Figure 11.7. Assume that we have two processors. The root node is expanded to generate two nodes (A and B), and each of these nodes is assigned to one of the processors. Each processor now searches the subtrees rooted at its assigned node independently. At this point, the problem with static node assignment becomes apparent. The processor exploring the subtree rooted at node A expands considerably fewer nodes than does the other processor. Due to this imbalance in the workload, one processor is idle for a significant amount of time, reducing efficiency. Using a larger number of processors worsens the imbalance. Consider the partitioning of the tree for four processors. Nodes A and B are expanded to generate nodes C, D, E, and F. Assume that each of these nodes is assigned to one of the four processors. Now the processor searching the subtree rooted at node E does most of the work, and those searching the subtrees rooted at nodes C and D spend most of their time idle. The static partitioning of unstructured trees yields poor performance because of substantial variation in the size of partitions of the search space rooted at different nodes. Furthermore, since the search space is usually generated dynamically, it is difficult to get a good estimate of the size of the search space beforehand. Therefore, it is necessary to balance the search space among processors dynamically.
In dynamic load balancing, when a processor runs out of work, it gets more work from another processor that has work. Consider the two-processor partitioning of the tree in Figure 11.7(a). Assume that nodes A and B are assigned to the two processors as we just described. In this case when the processor searching the subtree rooted at node A runs out of work, it requests work from the other processor. Although the dynamic distribution of work results in communication overhead for work requests and work transfers, it reduces load imbalance among processors. This section explores several schemes for dynamically balancing the load between processors.
A parallel formulation of DFS based on dynamic load balancing is as follows. Each processor performs DFS on a disjoint part of the search space. When a processor finishes searching its part of the search space, it requests an unsearched part from other processors. This takes the form of work request and response messages in message passing architectures, and locking and extracting work in shared address space machines. Whenever a processor finds a goal node, all the processors terminate. If the search space is finite and the problem has no solutions, then all the processors eventually run out of work, and the algorithm terminates.
Since each processor searches the state space depth-first, unexplored states can be conveniently stored as a stack. Each processor maintains its own local stack on which it executes DFS. When a processor’s local stack is empty, it requests (either via explicit messages or by locking) untried alternatives from another processor’s stack. In the beginning, the entire search space is assigned to one processor, and other processors are assigned null search spaces (that is, empty stacks). The search space is distributed among the processors as they request work. We refer to the processor that sends work as the donor processor and to the processor that requests and receives work as the recipient processor.
As illustrated in Figure 11.8, each processor can be in one of two states: active (that is, it has work) or idle (that is, it is trying to get work). In message passing architectures, an idle processor selects a donor processor and sends it a work request. If the idle processor receives work (part of the state space to be searched) from the donor processor, it becomes active. If it receives a reject message (because the donor has no work), it selects another donor and sends a work request to that donor. This process repeats until the processor gets work or all the processors become idle. When a processor is idle and it receives a work request, that processor returns a reject message. The same process can be implemented on shared address space machines by locking another processors’ stack, examining it to see if it has work, extracting work, and unlocking the stack.
On message passing architectures, in the active state, a processor does a fixed amount of work (expands a fixed number of nodes) and then checks for pending work requests. When a work request is received, the processor partitions its work into two parts and sends one part to the requesting processor. When a processor has exhausted its own search space, it becomes idle. This process continues until a solution is found or until the entire space has been searched. If a solution is found, a message is broadcast to all processors to stop searching. A termination detection algorithm is used to detect whether all processors have become idle without finding a solution (Section 11.4.4).
Two characteristics of parallel DFS are critical to determining its performance. First is the method for splitting work at a processor, and the second is the scheme to determine the donor processor when a processor becomes idle.
When work is transferred, the donor’s stack is split into two stacks, one of which is sent to the recipient. In other words, some of the nodes (that is, alternatives) are removed from the donor’s stack and added to the recipient’s stack. If too little work is sent, the recipient quickly becomes idle; if too much, the donor becomes idle. Ideally, the stack is split into two equal pieces such that the size of the search space represented by each stack is the same. Such a split is called a half-split. It is difficult to get a good estimate of the size of the tree rooted at an unexpanded alternative in the stack. However, the alternatives near the bottom of the stack (that is, close to the initial node) tend to have bigger trees rooted at them, and alternatives near the top of the stack tend to have small trees rooted at them. To avoid sending very small amounts of work, nodes beyond a specified stack depth are not given away. This depth is called the cutoff depth.
Some possible strategies for splitting the search space are (1) send nodes near the bottom of the stack, (2) send nodes near the cutoff depth, and (3) send half the nodes between the bottom of the stack and the cutoff depth. The suitability of a splitting strategy depends on the nature of the search space. If the search space is uniform, both strategies 1 and 3 work well. If the search space is highly irregular, strategy 3 usually works well. If a strong heuristic is available (to order successors so that goal nodes move to the left of the state-space tree), strategy 2 is likely to perform better, since it tries to distribute those parts of the search space likely to contain a solution. The cost of splitting also becomes important if the stacks are deep. For such stacks, strategy 1 has lower cost than strategies 2 and 3.
Figure 11.9 shows the partitioning of the DFS tree of Figure 11.5(a) into two subtrees using strategy 3. Note that the states beyond the cutoff depth are not partitioned. Figure 11.9 also shows the representation of the stack corresponding to the two subtrees. The stack representation used in the figure stores only the unexplored alternatives.
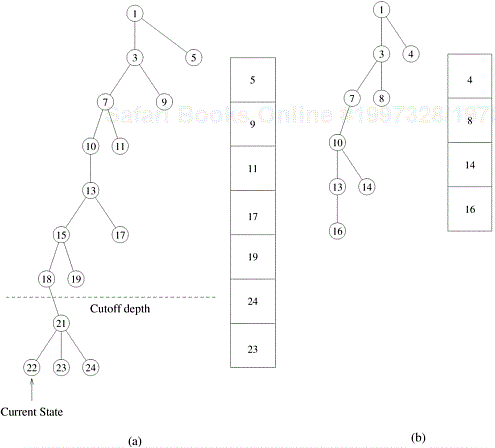
Figure 11.9. Splitting the DFS tree in Figure 11.5. The two subtrees along with their stack representations are shown in (a) and (b).
This section discusses three dynamic load-balancing schemes: asynchronous round robin, global round robin, and random polling. Each of these schemes can be coded for message passing as well as shared address space machines.
Asynchronous Round Robin. In asynchronous round robin (ARR), each processor maintains an independent variable, target. Whenever a processor runs out of work, it uses target as the label of a donor processor and attempts to get work from it. The value of target is incremented (modulo p) each time a work request is sent. The initial value of target at each processor is set to ((label + 1) modulo p) where label is the local processor label. Note that work requests are generated independently by each processor. However, it is possible for two or more processors to request work from the same donor at nearly the same time.
Global Round Robin. Global round robin (GRR) uses a single global variable called target. This variable can be stored in a globally accessible space in shared address space machines or at a designated processor in message passing machines. Whenever a processor needs work, it requests and receives the value of target, either by locking, reading, and unlocking on shared address space machines or by sending a message requesting the designated processor (say P0). The value of target is incremented (modulo p) before responding to the next request. The recipient processor then attempts to get work from a donor processor whose label is the value of target. GRR ensures that successive work requests are distributed evenly over all processors. A drawback of this scheme is the contention for access to target.
Random Polling. Random polling (RP) is the simplest load-balancing scheme. When a processor becomes idle, it randomly selects a donor. Each processor is selected as a donor with equal probability, ensuring that work requests are evenly distributed.
To analyze the performance and scalability of parallel DFS algorithms for any load-balancing scheme, we must compute the overhead To of the algorithm. Overhead in any load-balancing scheme is due to communication (requesting and sending work), idle time (waiting for work), termination detection, and contention for shared resources. If the search overhead factor is greater than one (i.e., if parallel search does more work than serial search), this will add another term to To. In this section we assume that the search overhead factor is one, i.e., the serial and parallel versions of the algorithm perform the same amount of computation. We analyze the case in which the search overhead factor is other than one in Section 11.6.1.
For the load-balancing schemes discussed in Section 11.4.1, idle time is subsumed by communication overhead due to work requests and transfers. When a processor becomes idle, it immediately selects a donor processor and sends it a work request. The total time for which the processor remains idle is equal to the time for the request to reach the donor and for the reply to arrive. At that point, the idle processor either becomes busy or generates another work request. Therefore, the time spent in communication subsumes the time for which a processor is idle. Since communication overhead is the dominant overhead in parallel DFS, we now consider a method to compute the communication overhead for each load-balancing scheme.
It is difficult to derive a precise expression for the communication overhead of the load-balancing schemes for DFS because they are dynamic. This section describes a technique that provides an upper bound on this overhead. We make the following assumptions in the analysis.
The work at any processor can be partitioned into independent pieces as long as its size exceeds a threshold ∊.
A reasonable work-splitting mechanism is available. Assume that work w at one processor is partitioned into two parts: ψw and (1 − ψ)w for 0 ≤ ψ ≤ 1. Then there exists an arbitrarily small constant α (0 < α ≤ 0.5), such that ψw > αw and (1 − ψ)w > αw. We call such a splitting mechanism α-splitting. The constant α sets a lower bound on the load imbalance that results from work splitting: both partitions of w have at least αw work.
The first assumption is satisfied by most depth-first search algorithms. The third work-splitting strategy described in Section 11.4.1 results in α-splitting even for highly irregular search spaces.
In the load-balancing schemes to be analyzed, the total work is dynamically partitioned among the processors. Processors work on disjoint parts of the search space independently. An idle processor polls for work. When it finds a donor processor with work, the work is split and a part of it is transferred to the idle processor. If the donor has work wi, and it is split into two pieces of size wj and wk, then assumption 2 states that there is a constant α such that wj > αwi and wk > αwi. Note that α is less than 0.5. Therefore, after a work transfer, neither processor (donor and recipient) has more than (1 − α)wi work. Suppose there are p pieces of work whose sizes are w0,w1, ..., wp−1. Assume that the size of the largest piece is w. If all of these pieces are split, the splitting strategy yields 2p pieces of work whose sizes are given by ψ0w0,ψ1w1, ..., ψp−1wp−1, (1 − ψ0)w0, (1 − ψ1)w1, ..., (1 − ψp−1)wp−1. Among them, the size of the largest piece is given by (1 − α)w.
Assume that there are p processors and a single piece of work is assigned to each processor. If every processor receives a work request at least once, then each of these p pieces has been split at least once. Thus, the maximum work at any of the processors has been reduced by a factor of (1 − α).We define V (p) such that, after every V (p) work requests, each processor receives at least one work request. Note that V (p) ≥ p. In general, V (p) depends on the load-balancing algorithm. Initially, processor P0 has W units of work, and all other processors have no work. After V (p) requests, the maximum work remaining at any processor is less than (1−α)W; after 2V (p) requests, the maximum work remaining at any processor is less than (1 − α)2W. Similarly, after (log1/(1−α)(W/∊))V (p) requests, the maximum work remaining at any processor is below a threshold value ∊. Hence, the total number of work requests is O (V (p) log W).
Communication overhead is caused by work requests and work transfers. The total number of work transfers cannot exceed the total number of work requests. Therefore, the total number of work requests, weighted by the total communication cost of one work request and a corresponding work transfer, gives an upper bound on the total communication overhead. For simplicity, we assume the amount of data associated with a work request and work transfer is a constant. In general, the size of the stack should grow logarithmically with respect to the size of the search space. The analysis for this case can be done similarly (Problem 11.3).
If tcomm is the time required to communicate a piece of work, then the communication overhead To is given by
The corresponding efficiency E is given by
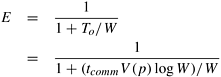
In Section 5.4.2 we showed that the isoefficiency function can be derived by balancing the problem size W and the overhead function To. As shown by Equation 11.2, To depends on two values: tcomm and V (p). The value of tcomm is determined by the underlying architecture, and the function V (p) is determined by the load-balancing scheme. In the following subsections, we derive V (p) for each scheme introduced in Section 11.4.1. We subsequently use these values of V (p) to derive the scalability of various schemes on message-passing and shared-address-space machines.
Equation 11.2 shows that V (p) is an important component of the total communication overhead. In this section, we compute the value of V (p) for different load-balancing schemes.
Asynchronous Round Robin. The worst case value of V (p) for ARR occurs when all processors issue work requests at the same time to the same processor. This case is illustrated in the following scenario. Assume that processor p − 1 had all the work and that the local counters of all the other processors (0 to p − 2) were pointing to processor zero. In this case, for processor p − 1 to receive a work request, one processor must issue p − 1 requests while each of the remaining p − 2 processors generates up to p − 2 work requests (to all processors except processor p − 1 and itself). Thus, V (p) has an upper bound of (p − 1) + (p − 2)(p − 2); that is, V (p) = O (p2). Note that the actual value of V (p) is between p and p2.
Global Round Robin. In GRR, all processors receive requests in sequence. After p requests, each processor has received one request. Therefore, V (p) is p.
Random Polling. For RR, the worst-case value of V (p) is unbounded. Hence, we compute the average-case value of V (p).
Consider a collection of p boxes. In each trial, a box is chosen at random and marked. We are interested in the mean number of trials required to mark all the boxes. In our algorithm, each trial corresponds to a processor sending another randomly selected processor a request for work.
Let F (i, p) represent a state in which i of the p boxes have been marked, and p − i boxes have not been marked. Since the next box to be marked is picked at random, there is i/p probability that it will be a marked box and (p − i)/p probability that it will be an unmarked box. Hence the system remains in state F (i, p) with a probability of i/p and transits to state F (i + 1, p) with a probability of (p − i)/p. Let f (i, p) denote the average number of trials needed to change from state F (i, p) to F (p, p). Then, V (p) = f (0, p). We have
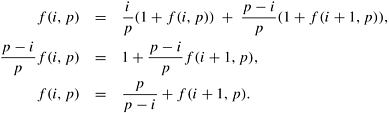
Hence,
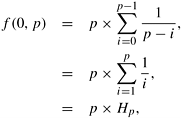
where Hp is a harmonic number. It can be shown that, as p becomes large, Hp ≃ 1.69 ln p (where ln p denotes the natural logarithm of p). Thus, V (p) = O (p log p).
This section analyzes the performance of the load-balancing schemes introduced in Section 11.4.1. In each case, we assume that work is transferred in fixed-size messages (the effect of relaxing this assumption is explored in Problem 11.3).
Recall that the cost of communicating an m-word message in the simplified cost model is tcomm = ts + twm. Since the message size m is assumed to be a constant, tcomm = O (1) if there is no congestion on the interconnection network. The communication overhead To (Equation 11.2) reduces to
We balance this overhead with problem size W for each load-balancing scheme to derive the isoefficiency function due to communication.
Asynchronous Round Robin. As discussed in Section 11.4.2, V (p) for ARR is O (p2). Substituting into Equation 11.3, communication overhead To is given by O (p2 log W). Balancing communication overhead against problem size W, we have
Substituting W into the right-hand side of the same equation and simplifying,
The double-log term (log log W) is asymptotically smaller than the first term, provided p grows no slower than log W, and can be ignored. The isoefficiency function for this scheme is therefore given by O ( p2 log p).
Global Round Robin. From Section 11.4.2, V (p) = O (p) for GRR. Substituting into Equation 11.3, this yields a communication overhead To of O (p log W). Simplifying as for ARR, the isoefficiency function for this scheme due to communication overhead is O (p log p).
In this scheme, however, the global variable target is accessed repeatedly, possibly causing contention. The number of times this variable is accessed is equal to the total number of work requests, O (p log W). If the processors are used efficiently, the total execution time is O (W/p). Assume that there is no contention for target while solving a problem of size W on p processors. Then, W/p is larger than the total time during which the shared variable is accessed. As the number of processors increases, the execution time (W/p) decreases, but the number of times the shared variable is accessed increases. Thus, there is a crossover point beyond which the shared variable becomes a bottleneck, prohibiting further reduction in run time. This bottleneck can be eliminated by increasing W at a rate such that the ratio between W/p and O (p log W) remains constant. This requires W to grow with respect to p as follows:
We can simplify Equation 11.4 to express W in terms of p. This yields an isoefficiency term of O (p2 log p).
Since the isoefficiency function due to contention asymptotically dominates the isoefficiency function due to communication, the overall isoefficiency function is given by O (p2 log p). Note that although it is difficult to estimate the actual overhead due to contention for the shared variable, we are able to determine the resulting isoefficiency function.
Random Polling. We saw in Section 11.4.2 that V (p) = O (p log p) for RP. Substituting this value into Equation 11.3, the communication overhead To is O (p log p log W). Equating To with the problem size W and simplifying as before, we derive the isoefficiency function due to communication overhead as O (p log2 p). Since there is no contention in RP, this function also gives its overall isoefficiency function.
One aspect of parallel DFS that has not been addressed thus far is termination detection. In this section, we present two schemes for termination detection that can be used with the load-balancing algorithms discussed in Section 11.4.1.
Consider a simplified scenario in which once a processor goes idle, it never receives more work. Visualize the p processors as being connected in a logical ring (note that a logical ring can be easily mapped to underlying physical topologies). Processor P0 initiates a token when it becomes idle. This token is sent to the next processor in the ring, P1. At any stage in the computation, if a processor receives a token, the token is held at the processor until the computation assigned to the processor is complete. On completion, the token is passed to the next processor in the ring. If the processor was already idle, the token is passed to the next processor. Note that if at any time the token is passed to processor Pi , then all processors P0, ..., Pi −1 have completed their computation. Processor Pp−1 passes its token to processor P0; when it receives the token, processor P0 knows that all processors have completed their computation and the algorithm can terminate.
Such a simple scheme cannot be applied to the search algorithms described in this chapter, because after a processor goes idle, it may receive more work from other processors. The token termination detection scheme thus must be modified.
In the modified scheme, the processors are also organized into a ring. A processor can be in one of two states: black or white. Initially, all processors are in state white. As before, the token travels in the sequence P0, P1, ..., Pp−1, P0. If the only work transfers allowed in the system are from processor Pi to Pj such that i < j, then the simple termination scheme is still adequate. However, if processor Pj sends work to processor Pi, the token must traverse the ring again. In this case processor Pj is marked black since it causes the token to go around the ring again. Processor P0 must be able to tell by looking at the token it receives whether it should be propagated around the ring again. Therefore the token itself is of two types: a white (or valid) token, which when received by processor P0 implies termination; and a black (or invalid) token, which implies that the token must traverse the ring again. The modified termination algorithm works as follows:
When it becomes idle, processor P0 initiates termination detection by making itself white and sending a white token to processor P1.
If processor Pj sends work to processor Pi and j > i then processor Pj becomes black.
If processor Pi has the token and Pi is idle, then it passes the token to Pi +1. If Pi is black, then the color of the token is set to black before it is sent to Pi +1. If Pi is white, the token is passed unchanged.
After Pi passes the token to Pi+1, Pi becomes white.
The algorithm terminates when processor P0 receives a white token and is itself idle. The algorithm correctly detects termination by accounting for the possibility of a processor receiving work after it has already been accounted for by the token.
The run time of this algorithm is O (P) with a small constant. For a small number of processors, this scheme can be used without a significant impact on the overall performance. For a large number of processors, this algorithm can cause the overall isoefficiency function of the load-balancing scheme to be at least O (p2) (Problem 11.4).
Tree-based termination detection associates weights with individual work pieces. Initially processor P0 has all the work and a weight of one is associated with it. When its work is partitioned and sent to another processor, processor P0 retains half of the weight and gives half of it to the processor receiving the work. If Pi is the recipient processor and wi is the weight at processor Pi, then after the first work transfer, both w0 and wi are 0.5. Each time the work at a processor is partitioned, the weight is halved. When a processor completes its computation, it returns its weight to the processor from which it received work. Termination is signaled when the weight w0 at processor P0 becomes one and processor P0 has finished its work.
Example 11.7 Tree-based termination detection
Figure 11.10 illustrates tree-based termination detection for four processors. Initially, processor P0 has all the weight (w0 = 1), and the weight at the remaining processors is 0 (w1 = w2 = w3 = 0). In step 1, processor P0 partitions its work and gives part of it to processor P1. After this step, w0 and w1 are 0.5 and w2 and w3 are 0. In step 2, processor P1 gives half of its work to processor P2. The weights w1 and w2 after this work transfer are 0.25 and the weights w0 and w3 remain unchanged. In step 3, processor P3 gets work from processor P1 and the weights of all processors become 0.25. In step 4, processor P2 completes its work and sends its weight to processor P1. The weight w1 of processor P1 becomes 0.5. As processors complete their work, weights are propagated up the tree until the weight w0 at processor P0 becomes 1. At this point, all work has been completed and termination can be signaled. ▪
This termination detection algorithm has a significant drawback. Due to the finite precision of computers, recursive halving of the weight may make the weight so small that it becomes 0. In this case, weight will be lost and termination will never be signaled. This condition can be alleviated by using the inverse of the weights. If processor Pi has weight wi, instead of manipulating the weight itself, it manipulates 1/wi. The details of this algorithm are considered in Problem 11.5.
The tree-based termination detection algorithm does not change the overall isoefficiency function of any of the search schemes we have considered. This follows from the fact that there are exactly two weight transfers associated with each work transfer. Therefore, the algorithm has the effect of increasing the communication overhead by a constant factor. In asymptotic terms, this change does not alter the isoefficiency function.
In this section, we demonstrate the validity of scalability analysis for various parallel DFS algorithms. The satisfiability problem tests the validity of boolean formulae. Such problems arise in areas such as VLSI design and theorem proving. The satisfiability problem can be stated as follows: given a boolean formula containing binary variables in conjunctive normal form, determine if it is unsatisfiable. A boolean formula is unsatisfiable if there exists no assignment of truth values to variables for which the formula is true.
The Davis-Putnam algorithm is a fast and efficient way to solve this problem. The algorithm works by performing a depth-first search of the binary tree formed by true or false assignments to the literals in the boolean expression. Let n be the number of literals. Then the maximum depth of the tree cannot exceed n. If, after a partial assignment of values to literals, the formula becomes false, then the algorithm backtracks. The formula is unsatisfiable if depth-first search fails to find an assignment to variables for which the formula is true.
Even if a formula is unsatisfiable, only a small subset of the 2n possible combinations will actually be explored. For example, for a 65-variable problem, the total number of possible combinations is 265 (approximately 3.7 × 1019), but only about 107 nodes are actually expanded in a specific problem instance. The search tree for this problem is pruned in a highly nonuniform fashion and any attempt to partition the tree statically results in an extremely poor load balance.
Table 11.1. Average speedups for various load-balancing schemes.
|
Number of processors | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Scheme |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
|
ARR |
7.506 |
14.936 |
29.664 |
57.721 |
103.738 |
178.92 |
259.372 |
284.425 |
|
GRR |
7.384 |
14.734 |
29.291 |
57.729 |
110.754 |
184.828 |
155.051 | |
|
RP |
7.524 |
15.000 |
29.814 |
58.857 |
114.645 |
218.255 |
397.585 |
660.582 |
The satisfiability problem is used to test the load-balancing schemes on a message passing parallel computer for up to 1024 processors. We implemented the Davis-Putnam algorithm, and incorporated the load-balancing algorithms discussed in Section 11.4.1. This program was run on several unsatisfiable formulae. By choosing unsatisfiable instances, we ensured that the number of nodes expanded by the parallel formulation is the same as the number expanded by the sequential one; any speedup loss was due only to the overhead of load balancing.
In the problem instances on which the program was tested, the total number of nodes in the tree varied between approximately 105 and 107. The depth of the trees (which is equal to the number of variables in the formula) varied between 35 and 65. Speedup was calculated with respect to the optimum sequential execution time for the same problem. Average speedup was calculated by taking the ratio of the cumulative time to solve all the problems in parallel using a given number of processors to the corresponding cumulative sequential time. On a given number of processors, the speedup and efficiency were largely determined by the tree size (which is roughly proportional to the sequential run time). Thus, speedup on similar-sized problems was quite similar.
Table 11.2. Number of requests generated for GRR and RP.
|
Number of processors | ||||||||
|---|---|---|---|---|---|---|---|---|
|
Scheme |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
|
GRR |
260 |
661 |
1572 |
3445 |
8557 |
17088 |
41382 |
72874 |
|
RP |
562 |
2013 |
5106 |
15060 |
46056 |
136457 |
382695 |
885872 |
All schemes were tested on a sample set of five problem instances. Table 11.1 shows the average speedup obtained by parallel algorithms using different load-balancing techniques. Figure 11.11 is a graph of the speedups obtained. Table 11.2 presents the total number of work requests made by RP and GRR for one problem instance. Figure 11.12 shows the corresponding graph and compares the number of messages generated with the expected values O (p log2 p) and O (p log p) for RP and GRR, respectively.
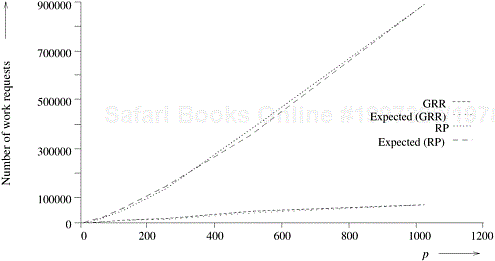
Figure 11.12. Number of work requests generated for RP and GRR and their expected values (O(p log2 p) and O(p log p) respectively).
The isoefficiency function of GRR is O (p2 log p) which is much worse than the isoefficiency function of RP. This is reflected in the performance of our implementation. From Figure 11.11, we see that the performance of GRR deteriorates very rapidly for more than 256 processors. Good speedups can be obtained for p > 256 only for very large problem instances. Experimental results also show that ARR is more scalable than GRR, but significantly less scalable than RP. Although the isoefficiency functions of ARR and GRR are both O (p2 log p), ARR performs better than GRR. The reason for this is that p2 log p is an upper bound, derived using V (p) = O (p2). This value of V (p) is only a loose upper bound for ARR. In contrast, the value of V (p) used for GRR (O (p)) is a tight bound.
To determine the accuracy of the isoefficiency functions of various schemes, we experimentally verified the isoefficiency curves for the RP technique (the selection of this technique was arbitrary). We ran 30 different problem instances varying in size from 105 nodes to 107 nodes on a varying number of processors. Speedup and efficiency were computed for each of these. Data points with the same efficiency for different problem sizes and number of processors were then grouped. Where identical efficiency points were not available, the problem size was computed by averaging over points with efficiencies in the neighborhood of the required value. These data are presented in Figure 11.13, which plots the problem size W against p log2 p for values of efficiency equal to 0.9, 0.85, 0.74, and 0.64. We expect points corresponding to the same efficiency to be collinear. We can see from Figure 11.13 that the points are reasonably collinear, which shows that the experimental isoefficiency function of RP is close to the theoretically derived isoefficiency function.
Parallel formulations of depth-first branch-and-bound search (DFBB) are similar to those of DFS. The preceding formulations of DFS can be applied to DFBB with one minor modification: all processors are kept informed of the current best solution path. The current best solution path for many problems can be represented by a small data structure. For shared address space computers, this data structure can be stored in a globally accessible memory. Each time a processor finds a solution, its cost is compared to that of the current best solution path. If the cost is lower, then the current best solution path is replaced. On a message-passing computer, each processor maintains the current best solution path known to it. Whenever a processor finds a solution path better than the current best known, it broadcasts its cost to all other processors, which update (if necessary) their current best solution cost. Since the cost of a solution is captured by a single number and solutions are found infrequently, the overhead of communicating this value is fairly small. Note that, if a processor’s current best solution path is worse than the globally best solution path, the efficiency of the search is affected but not its correctness. Because of DFBB’s low communication overhead, the performance and scalability of parallel DFBB is similar to that of parallel DFS discussed earlier.
Since IDA* explores the search tree iteratively with successively increasing cost bounds, it is natural to conceive a parallel formulation in which separate processors explore separate parts of the search space independently. Processors may be exploring the tree using different cost bounds. This approach suffers from two drawbacks.
It is unclear how to select a threshold for a particular processor. If the threshold chosen for a processor happens to be higher than the global minimum threshold, then the processor will explore portions of the tree that are not explored by sequential IDA*.
This approach may not find an optimal solution. A solution found by one processor in a particular iteration is not provably optimal until all the other processors have also exhausted the search space associated with thresholds lower than the cost of the solution found.
A more effective approach executes each iteration of IDA* by using parallel DFS (Section 11.4). All processors use the same cost bound; each processor stores the bound locally and performs DFS on its own search space. After each iteration of parallel IDA*, a designated processor determines the cost bound for the next iteration and restarts parallel DFS with the new bound. The search terminates when a processor finds a goal node and informs all the other processors. The performance and scalability of this parallel formulation of IDA* are similar to those of the parallel DFS algorithm.
Recall from Section 11.2.2 that an important component of best-first search (BFS) algorithms is the open list. It maintains the unexpanded nodes in the search graph, ordered according to their l-value. In the sequential algorithm, the most promising node from the open list is removed and expanded, and newly generated nodes are added to the open list.
In most parallel formulations of BFS, different processors concurrently expand different nodes from the open list. These formulations differ according to the data structures they use to implement the open list. Given p processors, the simplest strategy assigns each processor to work on one of the current best nodes on the open list. This is called the centralized strategy because each processor gets work from a single global open list. Since this formulation of parallel BFS expands more than one node at a time, it may expand nodes that would not be expanded by a sequential algorithm. Consider the case in which the first node on the open list is a solution. The parallel formulation still expands the first p nodes on the open list. However, since it always picks the best p nodes, the amount of extra work is limited. Figure 11.14 illustrates this strategy. There are two problems with this approach:
The termination criterion of sequential BFS fails for parallel BFS. Since at any moment, p nodes from the open list are being expanded, it is possible that one of the nodes may be a solution that does not correspond to the best goal node (or the path found is not the shortest path). This is because the remaining p − 1 nodes may lead to search spaces containing better goal nodes. Therefore, if the cost of a solution found by a processor is c, then this solution is not guaranteed to correspond to the best goal node until the cost of nodes being searched at other processors is known to be at least c. The termination criterion must be modified to ensure that termination occurs only after the best solution has been found.
Since the open list is accessed for each node expansion, it must be easily accessible to all processors, which can severely limit performance. Even on shared-address-space architectures, contention for the open list limits speedup. Let texp be the average time to expand a single node, and taccess be the average time to access the open list for a single-node expansion. If there are n nodes to be expanded by both the sequential and parallel formulations (assuming that they do an equal amount of work), then the sequential run time is given by n(taccess + texp). Assume that it is impossible to parallelize the expansion of individual nodes. Then the parallel run time will be at least ntaccess, because the open list must be accessed at least once for each node expanded. Hence, an upper bound on the speedup is (taccess + texp)/taccess.
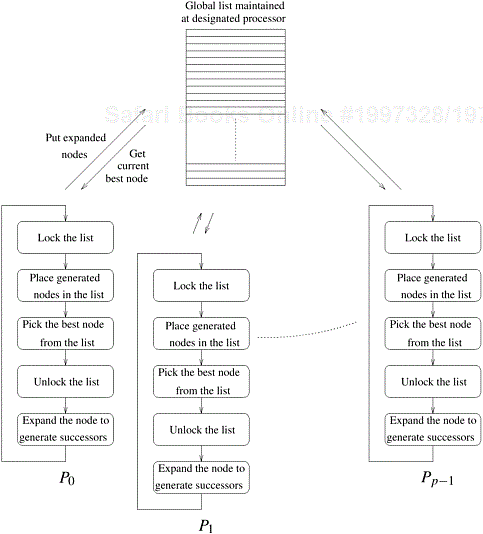
Figure 11.14. A general schematic for parallel best-first search using a centralized strategy. The locking operation is used here to serialize queue access by various processors.
One way to avoid the contention due to a centralized open list is to let each processor have a local open list. Initially, the search space is statically divided among the processors by expanding some nodes and distributing them to the local open lists of various processors. All the processors then select and expand nodes simultaneously. Consider a scenario where processors do not communicate with each other. In this case, some processors might explore parts of the search space that would not be explored by the sequential algorithm. This leads to a high search overhead factor and poor speedup. Consequently, the processors must communicate among themselves to minimize unnecessary search. The use of a distributed open list trades-off communication and computation: decreasing communication between distributed open lists increases search overhead factor, and decreasing search overhead factor with increased communication increases communication overhead.
The best choice of communication strategy for parallel BFS depends on whether the search space is a tree or a graph. Searching a graph incurs the additional overhead of checking for duplicate nodes on the closed list. We discuss some communication strategies for tree and graph search separately.
A communication strategy allows state-space nodes to be exchanged between open lists on different processors. The objective of a communication strategy is to ensure that nodes with good l-values are distributed evenly among processors. In this section we discuss three such strategies, as follows.
In the random communication strategy, each processor periodically sends some of its best nodes to the open list of a randomly selected processor. This strategy ensures that, if a processor stores a good part of the search space, the others get part of it. If nodes are transferred frequently, the search overhead factor can be made very small; otherwise it can become quite large. The communication cost determines the best node transfer frequency. If the communication cost is low, it is best to communicate after every node expansion.
In the ring communication strategy, the processors are mapped in a virtual ring. Each processor periodically exchanges some of its best nodes with the open lists of its neighbors in the ring. This strategy can be implemented on message passing as well as shared address space machines with the processors organized into a logical ring. As before, the cost of communication determines the node transfer frequency. Figure 11.15 illustrates the ring communication strategy.

Figure 11.15. A message-passing implementation of parallel best-first search using the ring communication strategy.
Unless the search space is highly uniform, the search overhead factor of this scheme is very high. The reason is that this scheme takes a long time to distribute good nodes from one processor to all other processors.
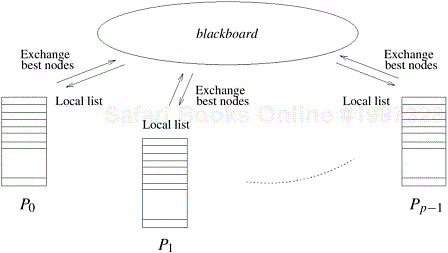
In the blackboard communication strategy, there is a shared blackboard through which nodes are switched among processors as follows. After selecting the best node from its local open list, a processor expands the node only if its l-value is within a tolerable limit of the best node on the blackboard. If the selected node is much better than the best node on the blackboard, the processor sends some of its best nodes to the blackboard before expanding the current node. If the selected node is much worse than the best node on the blackboard, the processor retrieves some good nodes from the blackboard and reselects a node for expansion. Figure 11.16 illustrates the blackboard communication strategy. The blackboard strategy is suited only to shared-address-space computers, because the value of the best node in the blackboard has to be checked after each node expansion.
While searching graphs, an algorithm must check for node replication. This task is distributed among processors. One way to check for replication is to map each node to a specific processor. Subsequently, whenever a node is generated, it is mapped to the same processor, which checks for replication locally. This technique can be implemented using a hash function that takes a node as input and returns a processor label. When a node is generated, it is sent to the processor whose label is returned by the hash function for that node. Upon receiving the node, a processor checks whether it already exists in the local open or closed lists. If not, the node is inserted in the open list. If the node already exists, and if the new node has a better cost associated with it, then the previous version of the node is replaced by the new node on the open list.
For a random hash function, the load-balancing property of this distribution strategy is similar to the random-distribution technique discussed in the previous section. This result follows from the fact that each processor is equally likely to be assigned a part of the search space that would also be explored by a sequential formulation. This method ensures an even distribution of nodes with good heuristic values among all the processors (Problem 11.10). However, hashing techniques degrade performance because each node generation results in communication (Problem 11.11).
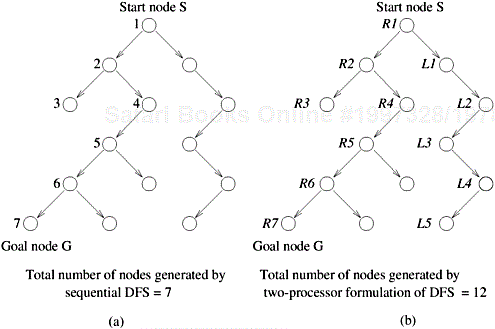
In parallel search algorithms, speedup can vary greatly from one execution to another because the portions of the search space examined by various processors are determined dynamically and can differ for each execution. Consider the case of sequential and parallel DFS performed on the tree illustrated in Figure 11.17. Figure 11.17(a) illustrates sequential DFS search. The order of node expansions is indicated by node labels. The sequential formulation generates 13 nodes before reaching the goal node G.

Figure 11.17. The difference in number of nodes searched by sequential and parallel formulations of DFS. For this example, parallel DFS reaches a goal node after searching fewer nodes than sequential DFS.
Now consider the parallel formulation of DFS illustrated for the same tree in Figure 11.17(b) for two processors. The nodes expanded by the processors are labeled R and L. The parallel formulation reaches the goal node after generating only nine nodes. That is, the parallel formulation arrives at the goal node after searching fewer nodes than its sequential counterpart. In this case, the search overhead factor is 9/13 (less than one), and if communication overhead is not too large, the speedup will be superlinear.
Finally, consider the situation in Figure 11.18. The sequential formulation (Figure 11.18(a)) generates seven nodes before reaching the goal node, but the parallel formulation generates 12 nodes. In this case, the search overhead factor is greater than one, resulting in sublinear speedup.
In summary, for some executions, the parallel version finds a solution after generating fewer nodes than the sequential version, making it possible to obtain superlinear speedup. For other executions, the parallel version finds a solution after generating more nodes, resulting in sublinear speedup. Executions yielding speedups greater than p by using p processors are referred to as acceleration anomalies. Speedups of less than p using p processors are called deceleration anomalies.
Speedup anomalies also manifest themselves in best-first search algorithms. Here, anomalies are caused by nodes on the open list that have identical heuristic values but require vastly different amounts of search to detect a solution. Assume that two such nodes exist; node A leads rapidly to the goal node, and node B leads nowhere after extensive work. In parallel BFS, both nodes are chosen for expansion by different processors. Consider the relative performance of parallel and sequential BFS. If the sequential algorithm picks node A to expand, it arrives quickly at a goal. However, the parallel algorithm wastes time expanding node B, leading to a deceleration anomaly. In contrast, if the sequential algorithm expands node B, it wastes substantial time before abandoning it in favor of node A. However, the parallel algorithm does not waste as much time on node B, because node A yields a solution quickly, leading to an acceleration anomaly.
In isolated executions of parallel search algorithms, the search overhead factor may be equal to one, less than one, or greater than one. It is interesting to know the average value of the search overhead factor. If it is less than one, this implies that the sequential search algorithm is not optimal. In this case, the parallel search algorithm running on a sequential processor (by emulating a parallel processor by using time-slicing) would expand fewer nodes than the sequential algorithm on the average. In this section, we show that for a certain type of search space, the average value of the search overhead factor in parallel DFS is less than one. Hence, if the communication overhead is not too large, then on the average, parallel DFS will provide superlinear speedup for this type of search space.
We make the following assumptions for analyzing speedup anomalies:
The state-space tree has M leaf nodes. Solutions occur only at leaf nodes. The amount of computation needed to generate each leaf node is the same. The number of nodes generated in the tree is proportional to the number of leaf nodes generated. This is a reasonable assumption for search trees in which each node has more than one successor on the average.
Both sequential and parallel DFS stop after finding one solution.
In parallel DFS, the state-space tree is equally partitioned among p processors; thus, each processor gets a subtree with M/p leaf nodes.
There is at least one solution in the entire tree. (Otherwise, both parallel search and sequential search generate the entire tree without finding a solution, resulting in linear speedup.)
There is no information to order the search of the state-space tree; hence, the density of solutions across the unexplored nodes is independent of the order of the search.
The solution density ρ is defined as the probability of the leaf node being a solution. We assume a Bernoulli distribution of solutions; that is, the event of a leaf node being a solution is independent of any other leaf node being a solution. We also assume that ρ ≪ 1.
The total number of leaf nodes generated by p processors before one of the processors finds a solution is denoted by Wp. The average number of leaf nodes generated by sequential DFS before a solution is found is given by W. Both W and Wp are less than or equal to M.
Consider the scenario in which the M leaf nodes are statically divided into p regions, each with K = M/p leaves. Let the density of solutions among the leaves in the ith region be ρi. In the parallel algorithm, each processor Pi searches region i independently until a processor finds a solution. In the sequential algorithm, the regions are searched in random order.
Note
Theorem 11.6.1. Let ρ be the solution density in a region; and assume that the number of leaves K in the region is large. Then, if ρ > 0, the mean number of leaves generated by a single processor searching the region is 1/ρ.
Proof: Since we have a Bernoulli distribution, the mean number of trials is given by
For a fixed value of ρ and a large value of K, the second term in Equation 11.5 becomes small; hence, the mean number of trials is approximately equal to 1/ρ. □
Sequential DFS selects any one of the p regions with probability 1/p and searches it to find a solution. Hence, the average number of leaf nodes expanded by sequential DFS is
This expression assumes that a solution is always found in the selected region; thus, only one region must be searched. However, the probability of region i not having any solutions is (1 − ρi)K. In this case, another region must be searched. Taking this into account makes the expression for W more precise and increases the average value of W somewhat. The overall results of the analysis will not change.
In each step of parallel DFS, one node from each of the p regions is explored simultaneously. Hence the probability of success in a step of the parallel algorithm is ![]() . This is approximately ρ1 + ρ2 + ··· + ρp (neglecting the second-order terms, since each ρi are assumed to be small). Hence,
. This is approximately ρ1 + ρ2 + ··· + ρp (neglecting the second-order terms, since each ρi are assumed to be small). Hence,
Inspecting the above equations, we see that W = 1/HM and Wp = 1/AM, where HM is the harmonic mean of ρ1, ρ2, ..., ρp, and AM is their arithmetic mean. Since the arithmetic mean (AM) and the harmonic mean (HM) satisfy the relation AM ≥ HM, we have W ≥ Wp. In particular:
When ρ1 = ρ2 = ··· = ρp, AM = HM, therefore W ≃ Wp. When solutions are uniformly distributed, the average search overhead factor for parallel DFS is one.
When each ρi is different, AM > HM, therefore W > Wp. When solution densities in various regions are nonuniform, the average search overhead factor for parallel DFS is less than one, making it possible to obtain superlinear speedups.
The assumption that each node can be a solution independent of the other nodes being solutions is false for most practical problems. Still, the preceding analysis suggests that parallel DFS obtains higher efficiency than sequential DFS provided that the solutions are not distributed uniformly in the search space and that no information about solution density in various regions is available. This characteristic applies to a variety of problem spaces searched by simple backtracking. The result that the search overhead factor for parallel DFS is at least one on the average is important, since DFS is currently the best known and most practical sequential algorithm used to solve many important problems.
Extensive literature is available on search algorithms for discrete optimization techniques such as branch-and-bound and heuristic search [KK88a, LW66, Pea84]. The relationship between branch-and-bound search, dynamic programming, and heuristic search techniques in artificial intelligence is explored by Kumar and Kanal [KK83, KK88b]. The average time complexity of heuristic search algorithms for many problems is shown to be polynomial by Smith [Smi84] and Wilf [Wil86]. Extensive work has been done on parallel formulations of search algorithms. We briefly outline some of these contributions.
Many parallel algorithms for DFS have been formulated [AJM88, FM87, KK94, KGR94, KR87b, MV87, Ran91, Rao90, SK90, SK89, Vor87a]. Load balancing is the central issue in parallel DFS. In this chapter, distribution of work in parallel DFS was done using stack splitting [KGR94, KR87b]. An alternative scheme for work-distribution is node splitting, in which only a single node is given out [FK88, FTI90, Ran91]
This chapter discussed formulations of state-space search in which a processor requests work when it goes idle. Such load-balancing schemes are called receiver-initiated schemes. In other load-balancing schemes, a processor that has work gives away part of its work to another processor (with or without receiving a request). These schemes are called sender-initiated schemes.
Several researchers have used receiver-initiated load-balancing schemes in parallel DFS [FM87, KR87b, KGR94]. Kumar et al. [KGR94] analyze these load-balancing schemes including global round robin, random polling, asynchronous round robin, and nearest neighbor. The description and analysis of these schemes in Section 11.4 is based on the papers by Kumar et al. [KGR94, KR87b].
Parallel DFS using sender-initiated load balancing has been proposed by some researchers [FK88, FTI90, PFK90, Ran91, SK89]. Furuichi et al. propose the single-level and multilevel sender-based schemes [FTI90]. Kimura and Nobuyuki [KN91] presented the scalability analysis of these schemes. Ferguson and Korf [FK88, PFK90] present a load-balancing scheme called distributed tree search (DTS).
Other techniques using randomized allocation have been presented for parallel DFS of state-space trees [KP92, Ran91, SK89, SK90]. Issues relating to granularity control in parallel DFS have also been explored [RK87, SK89].
Saletore and Kale [SK90] present a formulation of parallel DFS in which nodes are assigned priorities and are expanded accordingly. They show that the search overhead factor of this prioritized DFS formulation is very close to one, allowing it to yield consistently increasing speedups with an increasing number of processors for sufficiently large problems.
In some parallel formulations of depth-first search, the state space is searched independently in a random order by different processors [JAM87, JAM88]. Challou et al. [CGK93] and Ertel [Ert92] show that such methods are useful for solving robot motion planning and theorem proving problems, respectively.
Most generic DFS formulations apply to depth-first branch-and-bound and IDA*. Some researchers have specifically studied parallel formulations of depth-first branch-and-bound [AKR89, AKR90, EDH80]. Many parallel formulations of IDA* have been proposed [RK87, RKR87, KS91a, PKF92, MD92].
Most of the parallel DFS formulations are suited only for MIMD computers. Due to the nature of the search problem, SIMD computers were considered inherently unsuitable for parallel search. However, work by Frye and Myczkowski [FM92], Powley et al. [PKF92], and Mahanti and Daniels [MD92] showed that parallel depth-first search techniques can be developed even for SIMD computers. Karypis and Kumar [KK94] presented parallel DFS schemes for SIMD computers that are as scalable as the schemes for MIMD computers.
Several researchers have experimentally evaluated parallel DFS. Finkel and Manber [FM87] present performance results for problems such as the traveling salesman problem and the knight’s tour for the Crystal multicomputer developed at the University of Wisconsin. Monien and Vornberger [MV87] show linear speedups on a network of transputers for a variety of combinatorial problems. Kumar et al. [AKR89, AKR90, AKRS91, KGR94] show linear speedups for problems such as the 15-puzzle, tautology verification, and automatic test pattern generation for various architectures such as a 128-processor BBN Butterfly, a 128-processor Intel iPSC, a 1024-processor nCUBE 2, and a 128-processor Symult 2010. Kumar, Grama, and Rao [GKR91, KGR94, KR87b, RK87] have investigated the scalability and performance of many of these schemes for hypercubes, meshes, and networks of workstations. Experimental results in Section 11.4.5 are taken from the paper by Kumar, Grama, and Rao [KGR94].
Parallel formulations of DFBB have also been investigated by several researchers. Many of these formulations are based on maintaining a current best solution, which is used as a global bound. It has been shown that the overhead for maintaining the current best solution tends to be a small fraction of the overhead for dynamic load balancing. Parallel formulations of DFBB have been shown to yield near linear speedups for many problems and architectures [ST95, LM97, Eck97, Eck94, AKR89].
Many researchers have proposed termination detection algorithms for use in parallel search. Dijkstra [DSG83] proposed the ring termination detection algorithm. The termination detection algorithm based on weights, discussed in Section 11.4.4, is similar to the one proposed by Rokusawa et al. [RICN88]. Dutt and Mahapatra [DM93] discuss the termination detection algorithm based on minimum spanning trees.
Alpha-beta search is essentially a depth-first branch-and-bound search technique that finds an optimal solution tree of an AND/OR graph [KK83, KK88b]. Many researchers have developed parallel formulations of alpha-beta search [ABJ82, Bau78, FK88, FF82, HB88, Lin83, MC82, MFMV90, MP85, PFK90]. Some of these methods have shown reasonable speedups on dozens of processors [FK88, MFMV90, PFK90].
The utility of parallel processing has been demonstrated in the context of a number of games, and in particular, chess. Work on large scale parallel α − β search led to the development of Deep Thought [Hsu90] in 1990. This program was capable of playing chess at grandmaster level. Subsequent advances in the use of dedicated hardware, parallel processing, and algorithms resulted in the development of IBM’s Deep Blue [HCH95, HG97] that beat the reigning world champion Gary Kasparov. Feldmann et al. [FMM94] developed a distributed chess program that is acknowledged to be one of the best computer chess players based entirely on general purpose hardware.
Many researchers have investigated parallel formulations of A* and branch-and-bound algorithms [KK84, KRR88, LK85, MV87, Qui89, HD89a, Vor86, WM84, Rao90, GKP92, AM88, CJP83, KB57, LP92, Rou87, PC89, PR89, PR90, PRV88, Ten90, MRSR92, Vor87b, Moh83, MV85, HD87]. All these formulations use different data structures to store the open list. Some formulations use the centralized strategy [Moh83, HD87]; some use distributed strategies such as the random communication strategy [Vor87b, Dal87, KRR88], the ring communication strategy [Vor86, WM84]; and the blackboard communication strategy [KRR88]. Kumar et al. [KRR88] experimentally evaluated the centralized strategy and some distributed strategies in the context of the traveling salesman problem, the vertex cover problem and the 15-puzzle. Dutt and Mahapatra [DM93, MD93] have proposed and evaluated a number of other communication strategies.
Manzini analyzed the hashing technique for distributing nodes in parallel graph search [MS90]. Evett et al. [EHMN90] proposed parallel retracting A* (PRA*), which operates under limited-memory conditions. In this formulation, each node is hashed to a unique processor. If a processor receives more nodes than it can store locally, it retracts nodes with poorer heuristic values. These retracted nodes are reexpanded when more promising nodes fail to yield a solution.
Karp and Zhang [KZ88] analyze the performance of parallel best-first branch-and-bound (that is, A*) by using a random distribution of nodes for a specific model of search trees. Renolet et al. [RDK89] use Monte Carlo simulations to model the performance of parallel best-first search. Wah and Yu [WY85] present stochastic models to analyze the performance of parallel formulations of depth-first branch-and-bound and best-first branch-and-bound search.
Bixby [Bix91] presents a parallel branch-and-cut algorithm to solve the symmetric traveling salesman problem. He also presents solutions of the LP relaxations of airline crew-scheduling models. Miller et al. [Mil91] present parallel formulations of the best-first branch-and-bound technique for solving the asymmetric traveling salesman problem on heterogeneous network computer architectures. Roucairol [Rou91] presents parallel best-first branch-and-bound formulations for shared-address-space computers and uses them to solve the multiknapsack and quadratic-assignment problems.
Many researchers have analyzed speedup anomalies in parallel search algorithms [IYF79, LS84, Kor81, LW86, MVS86, RKR87]. Lai and Sahni [LS84] present early work quantifying speedup anomalies in best-first search. Lai and Sprague [LS86] present enhancements and extensions to this work. Lai and Sprague [LS85] also present an analytical model and derive characteristics of the lower-bound function for which anomalies are guaranteed not to occur as the number of processors is increased. Li and Wah [LW84, LW86] and Wah et al. [WLY84] investigate dominance relations and heuristic functions and their effect on detrimental (speedup of < 1using p processors) and acceleration anomalies. Quinn and Deo [QD86] derive an upper bound on the speedup attainable by any parallel formulation of the branch-and-bound algorithm using the best-bound search strategy. Rao and Kumar [RK88b, RK93] analyze the average speedup in parallel DFS for two separate models with and without heuristic ordering information. They show that the search overhead factor in these cases is at most one. Section 11.6.1 is based on the results of Rao and Kumar [RK93].
Finally, many programming environments have been developed for implementing parallel search. Some examples are DIB [FM87], Chare-Kernel [SK89], MANIP [WM84], and PICOS [RDK89].
Heuristics form the most important component of search techniques, and parallel formulations of search algorithms must be viewed in the context of these heuristics. In BFS techniques, heuristics focus search by lowering the effective branching factor. In DFBB methods, heuristics provide better bounds, and thus serve to prune the search space.
Often, there is a tradeoff between the strength of the heuristic and the effective size of search space. Better heuristics result in smaller search spaces but are also more expensive to compute. For example, an important application of strong heuristics is in the computation of bounds for mixed integer programming (MIP). Mixed integer programming has seen significant advances over the years [JNS97]. Whereas 15 years back, MIP problems with 100 integer variables were considered challenging, today, many problems with up to 1000 integer variables can be solved on workstation class machines using branch-and-cut methods. The largest known instances of TSPs and QAPs have been solved using branch-and-bound with powerful heuristics [BMCP98, MP93]. The presence of effective heuristics may prune the search space considerably. For example, when Padberg and Rinaldi introduced the branch-and-cut algorithm in 1987, they used it to solve a 532 city TSP, which was the largest TSP solved optimally at that time. Subsequent improvements to the method led to the solution of a a 2392 city problem [PR91]. More recently, using cutting planes, problems with over 7000 cities have been solved [JNS97] on serial machines. However, for many problems of interest, the reduced search space still requires the use of parallelism [BMCP98, MP93, Rou87, MMR95]. Use of powerful heuristics combined with effective parallel processing has enabled the solution of extremely large problems [MP93]. For example, QAP problems from the Nugent and Eschermann test suites with up to 4.8 × 1010 nodes (Nugent22 with Gilmore-Lawler bound) were solved on a NEC Cenju-3 parallel computer in under nine days [BMCP98]. Another dazzling demonstration of this was presented by the IBM Deep Blue. Deep blue used a combination of dedicated hardware for generating and evaluating board positions and parallel search of the game tree using an IBM SP2 to beat the current world chess champion, Gary Kasparov [HCH95, HG97].
Heuristics have several important implications for exploiting parallelism. Strong heuristics narrow the state space and thus reduce the concurrency available in the search space. Use of powerful heuristics poses other computational challenges for parallel processing as well. For example, in branch-and-cut methods, a cut generated at a certain state may be required by other states. Therefore, in addition to balancing load, the parallel branch-and-cut formulation must also partition cuts among processors so that processors working in certain LP domains have access to the desired cuts [BCCL95, LM97, Eck97].
In addition to inter-node parallelism that has been discussed up to this point, intra-node parallelism can become a viable option if the heuristic is computationally expensive. For example, the assignment heuristic of Pekny et al. has been effectively parallelized for solving large instances of TSPs [MP93]. If the degree of inter-node parallelism is small, this form of parallelism provides a desirable alternative. Another example of this is in the solution of MIP problems using branch-and-cut methods. Branch-and-cut methods rely on LP relaxation for generating lower bounds of partially instantiated solutions followed by generation of valid inequalities [JNS97]. These LP relaxations constitute a major part of the overall computation time. Many of the industrial codes rely on Simplex to solve the LP problem since it can adapt the solution to added rows and columns. While interior point methods are better suited to parallelism, they tend to be less efficient for reoptimizing LP solutions with added rows and columns (in branch-and-cut methods). LP relaxation using Simplex has been shown to parallelize well on small numbers of processors but efforts to scale to larger numbers of processors have not been successful. LP based branch and bound methods have also been used for solving quadratic assignment problems using iterative solvers such as preconditioned Conjugate Gradient to approximately compute the interior point directions [PLRR94]. These methods have been used to compute lower bounds using linear programs with over 150,000 constraints and 300,000 variables for solving QAPs. These and other iterative solvers parallelize very effectively to a large number of processors. A general parallel framework for computing heuristic solutions to problems is presented by Pramanick and Kuhl [PK95].
11.1 [KGR94] In Section 11.4.1, we identified access to the global pointer, target, as a bottleneck in the GRR load-balancing scheme. Consider a modification of this scheme in which it is augmented with message combining. This scheme works as follows. All the requests to read the value of the global pointer target at processor zero are combined at intermediate processors. Thus, the total number of requests handled by processor zero is greatly reduced. This technique is essentially a software implementation of the fetch-and-add operation. This scheme is called GRR-M (GRR with message combining).
An implementation of this scheme is illustrated in Figure 11.19. Each processor is at a leaf node in a complete (logical) binary tree. Note that such a logical tree can be easily mapped on to a physical topology. When a processor wants to atomically read and increment target, it sends a request up the tree toward processor zero. An internal node of the tree holds a request from one of its children for at most time δ, then forwards the message to its parent. If a request comes from the node’s other child within time δ, the two requests are combined and sent up as a single request. If i is the total number of increment requests that have been combined, the resulting increment of target is i.
The returned value at each processor is equal to what it would have been if all the requests to target had been serialized. This is done as follows: each combined message is stored in a table at each processor until the request is granted. When the value of target is sent back to an internal node, two values are sent down to the left and right children if both requested a value of target. The two values are determined from the entries in the table corresponding to increment requests by the two children. The scheme is illustrated by Figure 11.19, in which the original value of target is x, and processors P0, P2, P4, P6 and P7 issue requests. The total requested increment is five. After the messages are combined and processed, the value of target received at these processors is x, x + 1, x + 2, x + 3 and x + 4, respectively.
Analyze the performance and scalability of this scheme for a message passing architecture.
11.2 [Lin92] Consider another load-balancing strategy. Assume that each processor maintains a variable called counter. Initially, each processor initializes its local copy of counter to zero. Whenever a processor goes idle, it searches for two processors Pi and Pi +1 in a logical ring embedded into any architecture, such that the value of counter at Pi is greater than that at Pi +1. The idle processor then sends a work request to processor Pi +1. If no such pair of processors exists, the request is sent to processor zero. On receiving a work request, a processor increments its local value of counter.
Devise algorithms to detect the pairs Pi and Pi +1. Analyze the scalability of this load-balancing scheme based on your algorithm to detect the pairs Pi and Pi +1 for a message passing architecture.
Hint: The upper bound on the number of work transfers for this scheme is similar to that for GRR.
11.3 In the analysis of various load-balancing schemes presented in Section 11.4.2, we assumed that the cost of transferring work is independent of the amount of work transferred. However, there are problems for which the work-transfer cost is a function of the amount of work transferred. Examples of such problems are found in tree-search applications for domains in which strong heuristics are available. For such applications, the size of the stack used to represent the search tree can vary significantly with the number of nodes in the search tree.
Consider a case in which the size of the stack for representing a search space of w nodes varies as
 . Assume that the load-balancing scheme used is GRR. Analyze the performance of this scheme for a message passing architecture.
. Assume that the load-balancing scheme used is GRR. Analyze the performance of this scheme for a message passing architecture.11.4 Consider Dijkstra’s token termination detection scheme described in Section 11.4.4. Show that the contribution of termination detection using this scheme to the overall isoefficiency function is O (p2). Comment on the value of the constants associated with this isoefficiency term.
11.5 Consider the tree-based termination detection scheme in Section 11.4.4. In this algorithm, the weights may become very small and may eventually become zero due to the finite precision of computers. In such cases, termination is never signaled. The algorithm can be modified by manipulating the reciprocal of the weight instead of the weight itself. Write the modified termination algorithm and show that it is capable of detecting termination correctly.
11.6 [DM93] Consider a termination detection algorithm in which a spanning tree of minimum diameter is mapped onto the architecture of the given parallel computer. The center of such a tree is a vertex with the minimum distance to the vertex farthest from it. The center of a spanning tree is considered to be its root.
While executing parallel search, a processor can be either idle or busy. The termination detection algorithm requires all work transfers in the system to be acknowledged by an ack message. A processor is busy if it has work, or if it has sent work to another processor and the corresponding ack message has not been received; otherwise the processor is idle. Processors at the leaves of the spanning tree send stop messages to their parent when they become idle. Processors at intermediate levels in the tree pass the stop message on to their parents when they have received stop messages from all their children and they themselves become idle. When the root processor receives stop messages from all its children and becomes idle, termination is signaled.
Since it is possible for a processor to receive work after it has sent a stop message to its parent, a processor signals that it has received work by sending a resume message to its parent. The resume message moves up the tree until it meets the previously issued stop message. On meeting the stop message, the resume message nullifies the stop message. An ack message is then sent to the processor that transferred part of its work.
Show using examples that this termination detection technique correctly signals termination. Determine the isoefficiency term due to this termination detection scheme for a spanning tree of depth log p.
11.7 [FTI90, KN91] Consider the single-level load-balancing scheme which works as follows: a designated processor called manager generates many subtasks and gives them one-by-one to the requesting processors on demand. The manager traverses the search tree depth-first to a predetermined cutoff depth and distributes nodes at that depth as subtasks. Increasing the cutoff depth increases the number of subtasks, but makes them smaller. The processors request another subtask from the manager only after finishing the previous one. Hence, if a processor gets subtasks corresponding to large subtrees, it will send fewer requests to the manager. If the cutoff depth is large enough, this scheme results in good load balance among the processors. However, if the cutoff depth is too large, the subtasks given out to the processors become small and the processors send more frequent requests to the manager. In this case, the manager becomes a bottleneck. Hence, this scheme has a poor scalability. Figure 11.20 illustrates the single-level work-distribution scheme.
Assume that the cost of communicating a piece of work between any two processors is negligible. Derive analytical expressions for the scalability of the single-level load-balancing scheme.
11.8 [FTI90, KN91] Consider the multilevel work-distribution scheme that circumvents the subtask generation bottleneck of the single-level scheme through multiple-level subtask generation. In this scheme, processors are arranged in an m-ary tree of depth d. The task of top-level subtask generation is given to the root processor. It divides the task into super-subtasks and distributes them to its successor processors on demand. These processors subdivide the super-subtasks into subtasks and distribute them to successor processors on request. The leaf processors repeatedly request work from their parents as soon as they have finished their previous work. A leaf processor is allocated to another subtask generator when its designated subtask generator runs out of work. For d = 1, the multi- and single-level schemes are identical. Comment on the performance and scalability of this scheme.
11.9 [FK88] Consider the distributed tree search scheme in which processors are allocated to separate parts of the search tree dynamically. Initially, all the processors are assigned to the root. When the root node is expanded (by one of the processors assigned to it), disjoint subsets of processors at the root are assigned to each successor, in accordance with a selected processor-allocation strategy. One possible processor-allocation strategy is to divide the processors equally among ancestor nodes. This process continues until there is only one processor assigned to a node. At this time, the processor searches the tree rooted at the node sequentially. If a processor finishes searching the search tree rooted at the node, it is reassigned to its parent node. If the parent node has other successor nodes still being explored, then this processor is allocated to one of them. Otherwise, the processor is assigned to its parent. This process continues until the entire tree is searched. Comment on the performance and scalability of this scheme.
11.10 Consider a parallel formulation of best-first search of a graph that uses a hash function to distribute nodes to processors (Section 11.5). The performance of this scheme is influenced by two factors: the communication cost and the number of “good” nodes expanded (a “good” node is one that would also be expanded by the sequential algorithm). These two factors can be analyzed independently of each other.
Assuming a completely random hash function (one in which each node has a probability of being hashed to a processor equal to 1/p), show that the expected number of nodes expanded by this parallel formulation differs from the optimal number by a constant factor (that is, independent of p). Assuming that the cost of communicating a node from one processor to another is O (1), derive the isoefficiency function of this scheme.
11.11 For the parallel formulation in Problem 11.10, assume that the number of nodes expanded by the sequential and parallel formulations are the same. Analyze the communication overhead of this formulation for a message passing architecture. Is the formulation scalable? If so, what is the isoefficiency function? If not, for what interconnection network would the formulation be scalable?
Hint: Note that a fully random hash function corresponds to an all-to-all personalized communication operation, which is bandwidth sensitive.