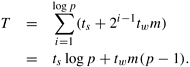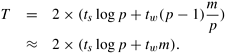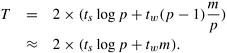In most parallel algorithms, processes need to exchange data with other processes. This exchange of data can significantly impact the efficiency of parallel programs by introducing interaction delays during their execution. For instance, recall from Section 2.5 that it takes roughly ts + mtw time for a simple exchange of an m-word message between two processes running on different nodes of an interconnection network with cut-through routing. Here ts is the latency or the startup time for the data transfer and tw is the per-word transfer time, which is inversely proportional to the available bandwidth between the nodes. Many interactions in practical parallel programs occur in well-defined patterns involving more than two processes. Often either all processes participate together in a single global interaction operation, or subsets of processes participate in interactions local to each subset. These common basic patterns of interprocess interaction or communication are frequently used as building blocks in a variety of parallel algorithms. Proper implementation of these basic communication operations on various parallel architectures is a key to the efficient execution of the parallel algorithms that use them.
In this chapter, we present algorithms to implement some commonly used communication patterns on simple interconnection networks, such as the linear array, two-dimensional mesh, and the hypercube. The choice of these interconnection networks is motivated primarily by pedagogical reasons. For instance, although it is unlikely that large scale parallel computers will be based on the linear array or ring topology, it is important to understand various communication operations in the context of linear arrays because the rows and columns of meshes are linear arrays. Parallel algorithms that perform rowwise or columnwise communication on meshes use linear array algorithms. The algorithms for a number of communication operations on a mesh are simple extensions of the corresponding linear array algorithms to two dimensions. Furthermore, parallel algorithms using regular data structures such as arrays often map naturally onto one- or two-dimensional arrays of processes. This too makes it important to study interprocess interaction on a linear array or mesh interconnection network. The hypercube architecture, on the other hand, is interesting because many algorithms with recursive interaction patterns map naturally onto a hypercube topology. Most of these algorithms may perform equally well on interconnection networks other than the hypercube, but it is simpler to visualize their communication patterns on a hypercube.
The algorithms presented in this chapter in the context of simple network topologies are practical and are highly suitable for modern parallel computers, even though most such computers are unlikely to have an interconnection network that exactly matches one of the networks considered in this chapter. The reason is that on a modern parallel computer, the time to transfer data of a certain size between two nodes is often independent of the relative location of the nodes in the interconnection network. This homogeneity is afforded by a variety of firmware and hardware features such as randomized routing algorithms and cut-through routing, etc. Furthermore, the end user usually does not have explicit control over mapping processes onto physical processors. Therefore, we assume that the transfer of m words of data between any pair of nodes in an interconnection network incurs a cost of ts + mtw. On most architectures, this assumption is reasonably accurate as long as a free link is available between the source and destination nodes for the data to traverse. However, if many pairs of nodes are communicating simultaneously, then the messages may take longer. This can happen if the number of messages passing through a cross-section of the network exceeds the cross-section bandwidth (Section 2.4.4) of the network. In such situations, we need to adjust the value of tw to reflect the slowdown due to congestion. As discussed in Section 2.5.1, we refer to the adjusted value of tw as effective tw. We will make a note in the text when we come across communication operations that may cause congestion on certain networks.
As discussed in Section 2.5.2, the cost of data-sharing among processors in the shared-address-space paradigm can be modeled using the same expression ts + mtw, usually with different values of ts and tw relative to each other as well as relative to the computation speed of the processors of the parallel computer. Therefore, parallel algorithms requiring one or more of the interaction patterns discussed in this chapter can be assumed to incur costs whose expression is close to one derived in the context of message-passing.
In the following sections we describe various communication operations and derive expressions for their time complexity. We assume that the interconnection network supports cut-through routing (Section 2.5.1) and that the communication time between any pair of nodes is practically independent of of the number of intermediate nodes along the paths between them. We also assume that the communication links are bidirectional; that is, two directly-connected nodes can send messages of size m to each other simultaneously in time ts + twm. We assume a single-port communication model, in which a node can send a message on only one of its links at a time. Similarly, it can receive a message on only one link at a time. However, a node can receive a message while sending another message at the same time on the same or a different link.
Many of the operations described here have duals and other related operations that we can perform by using procedures very similar to those for the original operations. The dual of a communication operation is the opposite of the original operation and can be performed by reversing the direction and sequence of messages in the original operation. We will mention such operations wherever applicable.
Parallel algorithms often require a single process to send identical data to all other processes or to a subset of them. This operation is known as one-to-all broadcast. Initially, only the source process has the data of size m that needs to be broadcast. At the termination of the procedure, there are p copies of the initial data – one belonging to each process. The dual of one-to-all broadcast is all-to-one reduction. In an all-to-one reduction operation, each of the p participating processes starts with a buffer M containing m words. The data from all processes are combined through an associative operator and accumulated at a single destination process into one buffer of size m. Reduction can be used to find the sum, product, maximum, or minimum of sets of numbers – the i th word of the accumulated M is the sum, product, maximum, or minimum of the i th words of each of the original buffers. Figure 4.1 shows one-to-all broadcast and all-to-one reduction among p processes.
One-to-all broadcast and all-to-one reduction are used in several important parallel algorithms including matrix-vector multiplication, Gaussian elimination, shortest paths, and vector inner product. In the following subsections, we consider the implementation of one-to-all broadcast in detail on a variety of interconnection topologies.
A naive way to perform one-to-all broadcast is to sequentially send p − 1 messages from the source to the other p − 1 processes. However, this is inefficient because the source process becomes a bottleneck. Moreover, the communication network is underutilized because only the connection between a single pair of nodes is used at a time. A better broadcast algorithm can be devised using a technique commonly known as recursive doubling. The source process first sends the message to another process. Now both these processes can simultaneously send the message to two other processes that are still waiting for the message. By continuing this procedure until all the processes have received the data, the message can be broadcast in log p steps.
The steps in a one-to-all broadcast on an eight-node linear array or ring are shown in Figure 4.2. The nodes are labeled from 0 to 7. Each message transmission step is shown by a numbered, dotted arrow from the source of the message to its destination. Arrows indicating messages sent during the same time step have the same number.

Figure 4.2. One-to-all broadcast on an eight-node ring. Node 0 is the source of the broadcast. Each message transfer step is shown by a numbered, dotted arrow from the source of the message to its destination. The number on an arrow indicates the time step during which the message is transferred.
Note that on a linear array, the destination node to which the message is sent in each step must be carefully chosen. In Figure 4.2, the message is first sent to the farthest node (4) from the source (0). In the second step, the distance between the sending and receiving nodes is halved, and so on. The message recipients are selected in this manner at each step to avoid congestion on the network. For example, if node 0 sent the message to node 1 in the first step and then nodes 0 and 1 attempted to send messages to nodes 2 and 3, respectively, in the second step, the link between nodes 1 and 2 would be congested as it would be a part of the shortest route for both the messages in the second step.
Reduction on a linear array can be performed by simply reversing the direction and the sequence of communication, as shown in Figure 4.3. In the first step, each odd numbered node sends its buffer to the even numbered node just before itself, where the contents of the two buffers are combined into one. After the first step, there are four buffers left to be reduced on nodes 0, 2, 4, and 6, respectively. In the second step, the contents of the buffers on nodes 0 and 2 are accumulated on node 0 and those on nodes 6 and 4 are accumulated on node 4. Finally, node 4 sends its buffer to node 0, which computes the final result of the reduction.
Example 4.1 Matrix-vector multiplication
Consider the problem of multiplying an n × n matrix A with an n × 1 vector x on an n × n mesh of nodes to yield an n × 1 result vector y. Algorithm 8.1 shows a serial algorithm for this problem. Figure 4.4 shows one possible mapping of the matrix and the vectors in which each element of the matrix belongs to a different process, and the vector is distributed among the processes in the topmost row of the mesh and the result vector is generated on the leftmost column of processes.

Figure 4.4. One-to-all broadcast and all-to-one reduction in the multiplication of a 4 × 4 matrix with a 4 × 1 vector.
Since all the rows of the matrix must be multiplied with the vector, each process needs the element of the vector residing in the topmost process of its column. Hence, before computing the matrix-vector product, each column of nodes performs a one-to-all broadcast of the vector elements with the topmost process of the column as the source. This is done by treating each column of the n × n mesh as an n-node linear array, and simultaneously applying the linear array broadcast procedure described previously to all columns.
After the broadcast, each process multiplies its matrix element with the result of the broadcast. Now, each row of processes needs to add its result to generate the corresponding element of the product vector. This is accomplished by performing all-to-one reduction on each row of the process mesh with the first process of each row as the destination of the reduction operation.
For example, P9 will receive x [1] from P1 as a result of the broadcast, will multiply it with A[2, 1] and will participate in an all-to-one reduction with P8, P10, and P11 to accumulate y[2] on P8. ▪
We can regard each row and column of a square mesh of p nodes as a linear array of ![]() nodes. So a number of communication algorithms on the mesh are simple extensions of their linear array counterparts. A linear array communication operation can be performed in two phases on a mesh. In the first phase, the operation is performed along one or all rows by treating the rows as linear arrays. In the second phase, the columns are treated similarly.
nodes. So a number of communication algorithms on the mesh are simple extensions of their linear array counterparts. A linear array communication operation can be performed in two phases on a mesh. In the first phase, the operation is performed along one or all rows by treating the rows as linear arrays. In the second phase, the columns are treated similarly.
Consider the problem of one-to-all broadcast on a two-dimensional square mesh with ![]() rows and
rows and ![]() columns. First, a one-to-all broadcast is performed from the source to the remaining (
columns. First, a one-to-all broadcast is performed from the source to the remaining (![]() ) nodes of the same row. Once all the nodes in a row of the mesh have acquired the data, they initiate a one-to-all broadcast in their respective columns. At the end of the second phase, every node in the mesh has a copy of the initial message. The communication steps for one-to-all broadcast on a mesh are illustrated in Figure 4.5 for p = 16, with node 0 at the bottom-left corner as the source. Steps 1 and 2 correspond to the first phase, and steps 3 and 4 correspond to the second phase.
) nodes of the same row. Once all the nodes in a row of the mesh have acquired the data, they initiate a one-to-all broadcast in their respective columns. At the end of the second phase, every node in the mesh has a copy of the initial message. The communication steps for one-to-all broadcast on a mesh are illustrated in Figure 4.5 for p = 16, with node 0 at the bottom-left corner as the source. Steps 1 and 2 correspond to the first phase, and steps 3 and 4 correspond to the second phase.
We can use a similar procedure for one-to-all broadcast on a three-dimensional mesh as well. In this case, rows of p1/3 nodes in each of the three dimensions of the mesh would be treated as linear arrays. As in the case of a linear array, reduction can be performed on two- and three-dimensional meshes by simply reversing the direction and the order of messages.
The previous subsection showed that one-to-all broadcast is performed in two phases on a two-dimensional mesh, with the communication taking place along a different dimension in each phase. Similarly, the process is carried out in three phases on a three-dimensional mesh. A hypercube with 2d nodes can be regarded as a d-dimensional mesh with two nodes in each dimension. Hence, the mesh algorithm can be extended to the hypercube, except that the process is now carried out in d steps – one in each dimension.
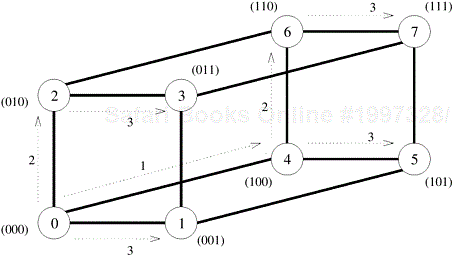
Figure 4.6 shows a one-to-all broadcast on an eight-node (three-dimensional) hypercube with node 0 as the source. In this figure, communication starts along the highest dimension (that is, the dimension specified by the most significant bit of the binary representation of a node label) and proceeds along successively lower dimensions in subsequent steps. Note that the source and the destination nodes in three communication steps of the algorithm shown in Figure 4.6 are identical to the ones in the broadcast algorithm on a linear array shown in Figure 4.2. However, on a hypercube, the order in which the dimensions are chosen for communication does not affect the outcome of the procedure. Figure 4.6 shows only one such order. Unlike a linear array, the hypercube broadcast would not suffer from congestion if node 0 started out by sending the message to node 1 in the first step, followed by nodes 0 and 1 sending messages to nodes 2 and 3, respectively, and finally nodes 0, 1, 2, and 3 sending messages to nodes 4, 5, 6, and 7, respectively.
The hypercube algorithm for one-to-all broadcast maps naturally onto a balanced binary tree in which each leaf is a processing node and intermediate nodes serve only as switching units. This is illustrated in Figure 4.7 for eight nodes. In this figure, the communicating nodes have the same labels as in the hypercube algorithm illustrated in Figure 4.6. Figure 4.7 shows that there is no congestion on any of the communication links at any time. The difference between the communication on a hypercube and the tree shown in Figure 4.7 is that there is a different number of switching nodes along different paths on the tree.
A careful look at Figures 4.2, 4.5, 4.6, and 4.7 would reveal that the basic communication pattern for one-to-all broadcast is identical on all the four interconnection networks considered in this section. We now describe procedures to implement the broadcast and reduction operations. For the sake of simplicity, the algorithms are described here in the context of a hypercube and assume that the number of communicating processes is a power of 2. However, they apply to any network topology, and can be easily extended to work for any number of processes (Problem 4.1).
Algorithm 4.1 shows a one-to-all broadcast procedure on a 2d-node network when node 0 is the source of the broadcast. The procedure is executed at all the nodes. At any node, the value of my_id is the label of that node. Let X be the message to be broadcast, which initially resides at the source node 0. The procedure performs d communication steps, one along each dimension of a hypothetical hypercube. In Algorithm 4.1, communication proceeds from the highest to the lowest dimension (although the order in which dimensions are chosen does not matter). The loop counter i indicates the current dimension of the hypercube in which communication is taking place. Only the nodes with zero in the i least significant bits of their labels participate in communication along dimension i. For instance, on the three-dimensional hypercube shown in Figure 4.6, i is equal to 2 in the first time step. Therefore, only nodes 0 and 4 communicate, since their two least significant bits are zero. In the next time step, when i = 1, all nodes (that is, 0, 2, 4, and 6) with zero in their least significant bits participate in communication. The procedure terminates after communication has taken place along all dimensions.
The variable mask helps determine which nodes communicate in a particular iteration of the loop. The variable mask has d (= log p) bits, all of which are initially set to one (Line 3). At the beginning of each iteration, the most significant nonzero bit of mask is reset to zero (Line 5). Line 6 determines which nodes communicate in the current iteration of the outer loop. For instance, for the hypercube of Figure 4.6, mask is initially set to 111, and it would be 011 during the iteration corresponding to i = 2 (the i least significant bits of mask are ones). The AND operation on Line 6 selects only those nodes that have zeros in their i least significant bits.
Among the nodes selected for communication along dimension i , the nodes with a zero at bit position i send the data, and the nodes with a one at bit position i receive it. The test to determine the sending and receiving nodes is performed on Line 7. For example, in Figure 4.6, node 0 (000) is the sender and node 4 (100) is the receiver in the iteration corresponding to i = 2. Similarly, for i = 1, nodes 0 (000) and 4 (100) are senders while nodes 2 (010) and 6 (110) are receivers.
Algorithm 4.1 works only if node 0 is the source of the broadcast. For an arbitrary source, we must relabel the nodes of the hypothetical hypercube by XORing the label of each node with the label of the source node before we apply this procedure. A modified one-to-all broadcast procedure that works for any value of source between 0 and p − 1 is shown in Algorithm 4.2. By performing the XOR operation at Line 3, Algorithm 4.2 relabels the source node to 0, and relabels the other nodes relative to the source. After this relabeling, the algorithm of Algorithm 4.1 can be applied to perform the broadcast.
Algorithm 4.3 gives a procedure to perform an all-to-one reduction on a hypothetical d-dimensional hypercube such that the final result is accumulated on node 0. Single node-accumulation is the dual of one-to-all broadcast. Therefore, we obtain the communication pattern required to implement reduction by reversing the order and the direction of messages in one-to-all broadcast. Procedure ALL_TO_ONE_REDUCE(d, my_id, m, X, sum) shown in Algorithm 4.3 is very similar to procedure ONE_TO_ALL_BC(d, my_id, X) shown in Algorithm 4.1. One difference is that the communication in all-to-one reduction proceeds from the lowest to the highest dimension. This change is reflected in the way that variables mask and i are manipulated in Algorithm 4.3. The criterion for determining the source and the destination among a pair of communicating nodes is also reversed (Line 7). Apart from these differences, procedure ALL_TO_ONE_REDUCE has extra instructions (Lines 13 and 14) to add the contents of the messages received by a node in each iteration (any associative operation can be used in place of addition).
Example 4.1. One-to-all broadcast of a message X from node 0 of a d-dimensional p-node hypercube (d = log p). AND and XOR are bitwise logical-and and exclusive-or operations, respectively.
1. procedure ONE_TO_ALL_BC(d, my_id, X) 2. begin 3. mask := 2d − 1; /* Set all d bits of mask to 1 */ 4. for i := d − 1 downto 0 do /* Outer loop */ 5. mask := mask XOR 2i; /* Set bit i of mask to 0 */ 6. if (my_id AND mask) = 0 then /* If lower i bits of my_id are 0 */ 7. if (my_id AND 2i) = 0 then 8. msg_destination := my_id XOR 2i; 9. send X to msg_destination; 10. else 11. msg_source := my_id XOR 2i; 12. receive X from msg_source; 13. endelse; 14. endif; 15. endfor; 16. end ONE_TO_ALL_BC
Example 4.2. One-to-all broadcast of a message X initiated by source on a d-dimensional hypothetical hypercube. The AND and XOR operations are bitwise logical operations.
1. procedure GENERAL_ONE_TO_ALL_BC(d, my_id, source, X) 2. begin 3. my_virtual id := my_id XOR source; 4. mask := 2d − 1; 5. for i := d − 1 downto 0 do /* Outer loop */ 6. mask := mask XOR 2i; /* Set bit i of mask to 0 */ 7. if (my_virtual_id AND mask) = 0 then 8. if (my_virtual_id AND 2i) = 0 then 9. virtual_dest := my_virtual_id XOR 2i; 10. send X to (virtual_dest XOR source); /* Convert virtual_dest to the label of the physical destination */ 11. else 12. virtual_source := my_virtual_id XOR 2i; 13. receive X from (virtual_source XOR source); /* Convert virtual_source to the label of the physical source */ 14. endelse; 15. endfor; 16. end GENERAL_ONE_TO_ALL_BC
Example 4.3. Single-node accumulation on a d-dimensional hypercube. Each node contributes a message X containing m words, and node 0 is the destination of the sum. The AND and XOR operations are bitwise logical operations.
1. procedure ALL_TO_ONE_REDUCE(d, my_id, m, X, sum) 2. begin 3. for j := 0 to m − 1 do sum[j] := X[j]; 4. mask := 0; 5. for i := 0 to d − 1 do /* Select nodes whose lower i bits are 0 */ 6. if (my_id AND mask) = 0 then 7. if (my_id AND 2i) ≠ 0 then 8. msg_destination := my_id XOR 2i; 9. send sum to msg_destination; 10. else 11. msg_source := my_id XOR 2i; 12. receive X from msg_source; 13. for j := 0 to m − 1 do 14. sum[j] :=sum[j] + X[j]; 15. endelse; 16. mask := mask XOR 2i; /* Set bit i of mask to 1 */ 17. endfor; 18. end ALL_TO_ONE_REDUCE
Analyzing the cost of one-to-all broadcast and all-to-one reduction is fairly straightforward. Assume that p processes participate in the operation and the data to be broadcast or reduced contains m words. The broadcast or reduction procedure involves log p point-to-point simple message transfers, each at a time cost of ts + tw m. Therefore, the total time taken by the procedure is
All-to-all broadcast is a generalization of one-to-all broadcast in which all p nodes simultaneously initiate a broadcast. A process sends the same m-word message to every other process, but different processes may broadcast different messages. All-to-all broadcast is used in matrix operations, including matrix multiplication and matrix-vector multiplication. The dual of all-to-all broadcast is all-to-all reduction, in which every node is the destination of an all-to-one reduction (Problem 4.8). Figure 4.8 illustrates all-to-all broadcast and all-to-all reduction.
One way to perform an all-to-all broadcast is to perform p one-to-all broadcasts, one starting at each node. If performed naively, on some architectures this approach may take up to p times as long as a one-to-all broadcast. It is possible to use the communication links in the interconnection network more efficiently by performing all p one-to-all broadcasts simultaneously so that all messages traversing the same path at the same time are concatenated into a single message whose size is the sum of the sizes of individual messages.
The following sections describe all-to-all broadcast on linear array, mesh, and hypercube topologies.
While performing all-to-all broadcast on a linear array or a ring, all communication links can be kept busy simultaneously until the operation is complete because each node always has some information that it can pass along to its neighbor. Each node first sends to one of its neighbors the data it needs to broadcast. In subsequent steps, it forwards the data received from one of its neighbors to its other neighbor.
Figure 4.9 illustrates all-to-all broadcast for an eight-node ring. The same procedure would also work on a linear array with bidirectional links. As with the previous figures, the integer label of an arrow indicates the time step during which the message is sent. In all-to-all broadcast, p different messages circulate in the p-node ensemble. In Figure 4.9, each message is identified by its initial source, whose label appears in parentheses along with the time step. For instance, the arc labeled 2 (7) between nodes 0 and 1 represents the data communicated in time step 2 that node 0 received from node 7 in the preceding step. As Figure 4.9 shows, if communication is performed circularly in a single direction, then each node receives all (p − 1) pieces of information from all other nodes in (p − 1) steps.

Figure 4.9. All-to-all broadcast on an eight-node ring. The label of each arrow shows the time step and, within parentheses, the label of the node that owned the current message being transferred before the beginning of the broadcast. The number(s) in parentheses next to each node are the labels of nodes from which data has been received prior to the current communication step. Only the first, second, and last communication steps are shown.
Algorithm 4.4 gives a procedure for all-to-all broadcast on a p-node ring. The initial message to be broadcast is known locally as my_msg at each node. At the end of the procedure, each node stores the collection of all p messages in result. As the program shows, all-to-all broadcast on a mesh applies the linear array procedure twice, once along the rows and once along the columns.
Example 4.4. All-to-all broadcast on a p-node ring.
1. procedure ALL_TO_ALL_BC_RING(my_id, my_msg, p, result) 2. begin 3. left := (my_id − 1) mod p; 4. right := (my_id + 1) mod p; 5. result := my_msg; 6. msg := result; 7. for i := 1 to p − 1 do 8. send msg to right; 9. receive msg from left; 10. result := result ∪ msg; 11. endfor; 12. end ALL_TO_ALL_BC_RING
In all-to-all reduction, the dual of all-to-all broadcast, each node starts with p messages, each one destined to be accumulated at a distinct node. All-to-all reduction can be performed by reversing the direction and sequence of the messages. For example, the first communication step for all-to-all reduction on an 8-node ring would correspond to the last step of Figure 4.9 with node 0 sending msg[1] to 7 instead of receiving it. The only additional step required is that upon receiving a message, a node must combine it with the local copy of the message that has the same destination as the received message before forwarding the combined message to the next neighbor. Algorithm 4.5 gives a procedure for all-to-all reduction on a p-node ring.
Example 4.5. All-to-all reduction on a p-node ring.
1. procedure ALL_TO_ALL_RED_RING(my_id, my_msg, p, result) 2. begin 3. left := (my_id − 1) mod p; 4. right := (my_id + 1) mod p; 5. recv := 0; 6. for i := 1 to p − 1 do 7. j := (my_id + i) mod p; 8. temp := msg[j] + recv; 9. send temp to left; 10. receive recv from right; 11. endfor; 12. result := msg[my_id] + recv; 13. end ALL_TO_ALL_RED_RING
Just like one-to-all broadcast, the all-to-all broadcast algorithm for the 2-D mesh is based on the linear array algorithm, treating rows and columns of the mesh as linear arrays. Once again, communication takes place in two phases. In the first phase, each row of the mesh performs an all-to-all broadcast using the procedure for the linear array. In this phase, all nodes collect ![]() messages corresponding to the
messages corresponding to the ![]() nodes of their respective rows. Each node consolidates this information into a single message of size
nodes of their respective rows. Each node consolidates this information into a single message of size ![]() , and proceeds to the second communication phase of the algorithm. The second communication phase is a columnwise all-to-all broadcast of the consolidated messages. By the end of this phase, each node obtains all p pieces of m-word data that originally resided on different nodes. The distribution of data among the nodes of a 3 × 3 mesh at the beginning of the first and the second phases of the algorithm is shown in Figure 4.10.
, and proceeds to the second communication phase of the algorithm. The second communication phase is a columnwise all-to-all broadcast of the consolidated messages. By the end of this phase, each node obtains all p pieces of m-word data that originally resided on different nodes. The distribution of data among the nodes of a 3 × 3 mesh at the beginning of the first and the second phases of the algorithm is shown in Figure 4.10.
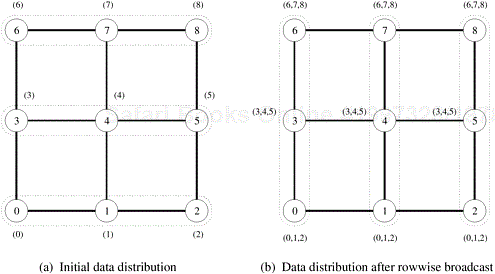
Figure 4.10. All-to-all broadcast on a 3 × 3 mesh. The groups of nodes communicating with each other in each phase are enclosed by dotted boundaries. By the end of the second phase, all nodes get (0,1,2,3,4,5,6,7) (that is, a message from each node).
Algorithm 4.6 gives a procedure for all-to-all broadcast on a ![]() mesh. The mesh procedure for all-to-all reduction is left as an exercise for the reader (Problem 4.4).
mesh. The mesh procedure for all-to-all reduction is left as an exercise for the reader (Problem 4.4).
Example 4.6. All-to-all broadcast on a square mesh of p nodes.
1. procedure ALL_TO_ALL_BC_MESH(my_id, my_msg, p, result) 2. begin /* Communication along rows */ 3. left := my_id − (my_id mod) + (my_id − 1)mod
; 4. right := my_id − (my_id mod
) + (my_id + 1) mod
; 5. result := my_msg; 6. msg := result; 7. for i := 1 to
− 1 do 8. send msg to right; 9. receive msg from left; 10. result := result ∪ msg; 11. endfor; /* Communication along columns */ 12. up := (my_id −
) mod p; 13. down := (my_id +
) mod p; 14. msg := result; 15. for i := 1 to
− 1 do 16. send msg to down; 17. receive msg from up; 18. result := result ∪ msg; 19. endfor; 20. end ALL_TO_ALL_BC_MESH
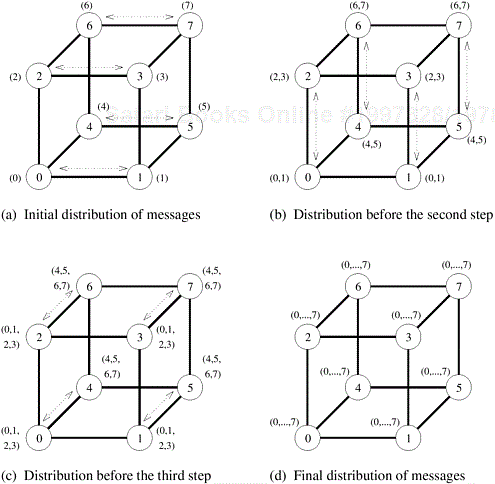
The hypercube algorithm for all-to-all broadcast is an extension of the mesh algorithm to log p dimensions. The procedure requires log p steps. Communication takes place along a different dimension of the p-node hypercube in each step. In every step, pairs of nodes exchange their data and double the size of the message to be transmitted in the next step by concatenating the received message with their current data. Figure 4.11 shows these steps for an eight-node hypercube with bidirectional communication channels.
Algorithm 4.7 gives a procedure for implementing all-to-all broadcast on a d-dimensional hypercube. Communication starts from the lowest dimension of the hypercube and then proceeds along successively higher dimensions (Line 4). In each iteration, nodes communicate in pairs so that the labels of the nodes communicating with each other in the i th iteration differ in the i th least significant bit of their binary representations (Line 5). After an iteration’s communication steps, each node concatenates the data it receives during that iteration with its resident data (Line 8). This concatenated message is transmitted in the following iteration.
Example 4.7. All-to-all broadcast on a d-dimensional hypercube.
1. procedure ALL_TO_ALL_BC_HCUBE(my_id, my_msg, d, result) 2. begin 3. result := my_msg; 4. for i := 0 to d − 1 do 5. partner := my id XOR 2i; 6. send result to partner; 7. receive msg from partner; 8. result := result ∪ msg; 9. endfor; 10. end ALL_TO_ALL_BC_HCUBE
As usual, the algorithm for all-to-all reduction can be derived by reversing the order and direction of messages in all-to-all broadcast. Furthermore, instead of concatenating the messages, the reduction operation needs to select the appropriate subsets of the buffer to send out and accumulate received messages in each iteration. Algorithm 4.8 gives a procedure for all-to-all reduction on a d-dimensional hypercube. It uses senloc to index into the starting location of the outgoing message and recloc to index into the location where the incoming message is added in each iteration.
Example 4.8. All-to-all broadcast on a d-dimensional hypercube. AND and XOR are bitwise logical-and and exclusive-or operations, respectively.
1. procedure ALL_TO_ALL_RED_HCUBE(my_id, msg, d, result) 2. begin 3. recloc := 0; 4. for i := d − 1 to 0 do 5. partner := my_id XOR 2i; 6. j := my_id AND 2i; 7. k := (my_id XOR 2i) AND 2i; 8. senloc := recloc + k; 9. recloc := recloc + j; 10. send msg[senloc .. senloc + 2i − 1] to partner; 11. receive temp[0 .. 2i − 1] from partner; 12. for j := 0 to 2i − 1 do 13. msg[recloc + j] := msg[recloc + j] + temp[j]; 14. endfor; 15. endfor; 16. result := msg[my_id]; 17. end ALL_TO_ALL_RED_HCUBE
On a ring or a linear array, all-to-all broadcast involves p − 1 steps of communication between nearest neighbors. Each step, involving a message of size m, takes time ts + tw m. Therefore, the time taken by the entire operation is
Similarly, on a mesh, the first phase of ![]() simultaneous all-to-all broadcasts (each among
simultaneous all-to-all broadcasts (each among ![]() nodes) concludes in time
nodes) concludes in time ![]() . The number of nodes participating in each all-to-all broadcast in the second phase is also
. The number of nodes participating in each all-to-all broadcast in the second phase is also ![]() , but the size of each message is now
, but the size of each message is now ![]() . Therefore, this phase takes time
. Therefore, this phase takes time ![]() to complete. The time for the entire all-to-all broadcast on a p-node two-dimensional square mesh is the sum of the times spent in the individual phases, which is
to complete. The time for the entire all-to-all broadcast on a p-node two-dimensional square mesh is the sum of the times spent in the individual phases, which is
On a p-node hypercube, the size of each message exchanged in the i th of the log p steps is 2i−1m. It takes a pair of nodes time ts + 2i−1twm to send and receive messages from each other during the i th step. Hence, the time to complete the entire procedure is
Equations 4.2, 4.3, and 4.4 show that the term associated with tw in the expressions for the communication time of all-to-all broadcast is twm(p − 1) for all the architectures. This term also serves as a lower bound for the communication time of all-to-all broadcast for parallel computers on which a node can communicate on only one of its ports at a time. This is because each node receives at least m(p − 1) words of data, regardless of the architecture. Thus, for large messages, a highly connected network like a hypercube is no better than a simple ring in performing all-to-all broadcast or all-to-all reduction. In fact, the straightforward all-to-all broadcast algorithm for a simple architecture like a ring has great practical importance. A close look at the algorithm reveals that it is a sequence of p one-to-all broadcasts, each with a different source. These broadcasts are pipelined so that all of them are complete in a total of p nearest-neighbor communication steps. Many parallel algorithms involve a series of one-to-all broadcasts with different sources, often interspersed with some computation. If each one-to-all broadcast is performed using the hypercube algorithm of Section 4.1.3, then n broadcasts would require time n(ts + twm) log p. On the other hand, by pipelining the broadcasts as shown in Figure 4.9, all of them can be performed spending no more than time (ts + twm)(p − 1) in communication, provided that the sources of all broadcasts are different and n ≤ p. In later chapters, we show how such pipelined broadcast improves the performance of some parallel algorithms such as Gaussian elimination (Section 8.3.1), back substitution (Section 8.3.3), and Floyd’s algorithm for finding the shortest paths in a graph (Section 10.4.2).
Another noteworthy property of all-to-all broadcast is that, unlike one-to-all broadcast, the hypercube algorithm cannot be applied unaltered to mesh and ring architectures. The reason is that the hypercube procedure for all-to-all broadcast would cause congestion on the communication channels of a smaller-dimensional network with the same number of nodes. For instance, Figure 4.12 shows the result of performing the third step (Figure 4.11(c)) of the hypercube all-to-all broadcast procedure on a ring. One of the links of the ring is traversed by all four messages and would take four times as much time to complete the communication step.

Figure 4.12. Contention for a channel when the communication step of Figure 4.11(c) for the hypercube is mapped onto a ring.
The communication pattern of all-to-all broadcast can be used to perform some other operations as well. One of these operations is a third variation of reduction, in which each node starts with a buffer of size m and the final results of the operation are identical buffers of size m on each node that are formed by combining the original p buffers using an associative operator. Semantically, this operation, often referred to as the all-reduce operation, is identical to performing an all-to-one reduction followed by a one-to-all broadcast of the result. This operation is different from all-to-all reduction, in which p simultaneous all-to-one reductions take place, each with a different destination for the result.
An all-reduce operation with a single-word message on each node is often used to implement barrier synchronization on a message-passing computer. The semantics of the reduction operation are such that, while executing a parallel program, no node can finish the reduction before each node has contributed a value.
A simple method to perform all-reduce is to perform an all-to-one reduction followed by a one-to-all broadcast. However, there is a faster way to perform all-reduce by using the communication pattern of all-to-all broadcast. Figure 4.11 illustrates this algorithm for an eight-node hypercube. Assume that each integer in parentheses in the figure, instead of denoting a message, denotes a number to be added that originally resided at the node with that integer label. To perform reduction, we follow the communication steps of the all-to-all broadcast procedure, but at the end of each step, add two numbers instead of concatenating two messages. At the termination of the reduction procedure, each node holds the sum (0 + 1 + 2 + ··· + 7) (rather than eight messages numbered from 0 to 7, as in the case of all-to-all broadcast). Unlike all-to-all broadcast, each message transferred in the reduction operation has only one word. The size of the messages does not double in each step because the numbers are added instead of being concatenated. Therefore, the total communication time for all log p steps is
Algorithm 4.7 can be used to perform a sum of p numbers if my_msg, msg, and result are numbers (rather than messages), and the union operation (‘∪’) on Line 8 is replaced by addition.
Finding prefix sums (also known as the scan operation) is another important problem that can be solved by using a communication pattern similar to that used in all-to-all broadcast and all-reduce operations. Given p numbers n0, n1, ..., np−1 (one on each node), the problem is to compute the sums ![]() for all k between 0 and p − 1. For example, if the original sequence of numbers is <3, 1, 4, 0, 2>, then the sequence of prefix sums is <3, 4, 8, 8, 10>. Initially, nk resides on the node labeled k, and at the end of the procedure, the same node holds sk . Instead of starting with a single numbers, each node could start with a buffer or vector of size m and the m-word result would be the sum of the corresponding elements of buffers.
for all k between 0 and p − 1. For example, if the original sequence of numbers is <3, 1, 4, 0, 2>, then the sequence of prefix sums is <3, 4, 8, 8, 10>. Initially, nk resides on the node labeled k, and at the end of the procedure, the same node holds sk . Instead of starting with a single numbers, each node could start with a buffer or vector of size m and the m-word result would be the sum of the corresponding elements of buffers.
Figure 4.13 illustrates the prefix sums procedure for an eight-node hypercube. This figure is a modification of Figure 4.11. The modification is required to accommodate the fact that in prefix sums the node with label k uses information from only the k-node subset of those nodes whose labels are less than or equal to k. To accumulate the correct prefix sum, every node maintains an additional result buffer. This buffer is denoted by square brackets in Figure 4.13. At the end of a communication step, the content of an incoming message is added to the result buffer only if the message comes from a node with a smaller label than that of the recipient node. The contents of the outgoing message (denoted by parentheses in the figure) are updated with every incoming message, just as in the case of the all-reduce operation. For instance, after the first communication step, nodes 0, 2, and 4 do not add the data received from nodes 1, 3, and 5 to their result buffers. However, the contents of the outgoing messages for the next step are updated.

Figure 4.13. Computing prefix sums on an eight-node hypercube. At each node, square brackets show the local prefix sum accumulated in the result buffer and parentheses enclose the contents of the outgoing message buffer for the next step.
Since not all of the messages received by a node contribute to its final result, some of the messages it receives may be redundant. We have omitted these steps of the standard all-to-all broadcast communication pattern from Figure 4.13, although the presence or absence of these messages does not affect the results of the algorithm. Algorithm 4.9 gives a procedure to solve the prefix sums problem on a d-dimensional hypercube.
Example 4.9. Prefix sums on a d-dimensional hypercube.
1. procedure PREFIX_SUMS_HCUBE(my_id, my number, d, result) 2. begin 3. result := my_number; 4. msg := result; 5. for i := 0 to d − 1 do 6. partner := my_id XOR 2i; 7. send msg to partner; 8. receive number from partner; 9. msg := msg + number; 10. if (partner < my_id) then result := result + number; 11. endfor; 12. end PREFIX_SUMS_HCUBE
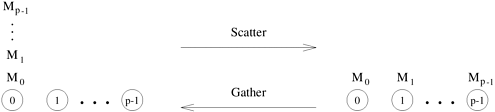
In the scatter operation, a single node sends a unique message of size m to every other node. This operation is also known as one-to-all personalized communication. One-to-all personalized communication is different from one-to-all broadcast in that the source node starts with p unique messages, one destined for each node. Unlike one-to-all broadcast, one-to-all personalized communication does not involve any duplication of data. The dual of one-to-all personalized communication or the scatter operation is the gather operation, or concatenation, in which a single node collects a unique message from each node. A gather operation is different from an all-to-one reduce operation in that it does not involve any combination or reduction of data. Figure 4.14 illustrates the scatter and gather operations.
Although the scatter operation is semantically different from one-to-all broadcast, the scatter algorithm is quite similar to that of the broadcast. Figure 4.15 shows the communication steps for the scatter operation on an eight-node hypercube. The communication patterns of one-to-all broadcast (Figure 4.6) and scatter (Figure 4.15) are identical. Only the size and the contents of messages are different. In Figure 4.15, the source node (node 0) contains all the messages. The messages are identified by the labels of their destination nodes. In the first communication step, the source transfers half of the messages to one of its neighbors. In subsequent steps, each node that has some data transfers half of it to a neighbor that has yet to receive any data. There is a total of log p communication steps corresponding to the log p dimensions of the hypercube.
The gather operation is simply the reverse of scatter. Each node starts with an m word message. In the first step, every odd numbered node sends its buffer to an even numbered neighbor behind it, which concatenates the received message with its own buffer. Only the even numbered nodes participate in the next communication step which results in nodes with multiples of four labels gathering more data and doubling the sizes of their data. The process continues similarly, until node 0 has gathered the entire data.
Just like one-to-all broadcast and all-to-one reduction, the hypercube algorithms for scatter and gather can be applied unaltered to linear array and mesh interconnection topologies without any increase in the communication time.
Cost Analysis. All links of a p-node hypercube along a certain dimension join two p/2-node subcubes (Section 2.4.3). As Figure 4.15 illustrates, in each communication step of the scatter operations, data flow from one subcube to another. The data that a node owns before starting communication in a certain dimension are such that half of them need to be sent to a node in the other subcube. In every step, a communicating node keeps half of its data, meant for the nodes in its subcube, and sends the other half to its neighbor in the other subcube. The time in which all data are distributed to their respective destinations is
The scatter and gather operations can also be performed on a linear array and on a 2-D square mesh in time ts log p + twm(p − 1) (Problem 4.7). Note that disregarding the term due to message-startup time, the cost of scatter and gather operations for large messages on any k-d mesh interconnection network (Section 2.4.3) is similar. In the scatter operation, at least m(p − 1) words of data must be transmitted out of the source node, and in the gather operation, at least m(p − 1) words of data must be received by the destination node. Therefore, as in the case of all-to-all broadcast, twm(p − 1) is a lower bound on the communication time of scatter and gather operations. This lower bound is independent of the interconnection network.
In all-to-all personalized communication, each node sends a distinct message of size m to every other node. Each node sends different messages to different nodes, unlike all-to-all broadcast, in which each node sends the same message to all other nodes. Figure 4.16 illustrates the all-to-all personalized communication operation. A careful observation of this figure would reveal that this operation is equivalent to transposing a two-dimensional array of data distributed among p processes using one-dimensional array partitioning (Figure 3.24). All-to-all personalized communication is also known as total exchange. This operation is used in a variety of parallel algorithms such as fast Fourier transform, matrix transpose, sample sort, and some parallel database join operations.
Example 4.2 Matrix transposition
The transpose of an n × n matrix A is a matrix AT of the same size, such that AT [i, j] = A[j, i] for 0 ≤ i, j < n. Consider an n × n matrix mapped onto n processors such that each processor contains one full row of the matrix. With this mapping, processor Pi initially contains the elements of the matrix with indices [i, 0], [i, 1], ..., [i, n − 1]. After the transposition, element [i, 0] belongs to P0, element [i, 1] belongs to P1, and so on. In general, element [i, j] initially resides on Pi , but moves to Pj during the transposition. The data-communication pattern of this procedure is shown in Figure 4.17 for a 4 × 4 matrix mapped onto four processes using one-dimensional rowwise partitioning. Note that in this figure every processor sends a distinct element of the matrix to every other processor. This is an example of all-to-all personalized communication.
Figure 4.17. All-to-all personalized communication in transposing a 4 × 4 matrix using four processes.
In general, if we use p processes such that p ≤ n, then each process initially holds n/p rows (that is, n2/p elements) of the matrix. Performing the transposition now involves an all-to-all personalized communication of matrix blocks of size n/p × n/p, instead of individual elements. ▪
We now discuss the implementation of all-to-all personalized communication on parallel computers with linear array, mesh, and hypercube interconnection networks. The communication patterns of all-to-all personalized communication are identical to those of all-to-all broadcast on all three architectures. Only the size and the contents of messages are different.
Figure 4.18 shows the steps in an all-to-all personalized communication on a six-node linear array. To perform this operation, every node sends p − 1 pieces of data, each of size m. In the figure, these pieces of data are identified by pairs of integers of the form {i, j}, where i is the source of the message and j is its final destination. First, each node sends all pieces of data as one consolidated message of size m(p − 1) to one of its neighbors (all nodes communicate in the same direction). Of the m(p − 1) words of data received by a node in this step, one m-word packet belongs to it. Therefore, each node extracts the information meant for it from the data received, and forwards the remaining (p − 2) pieces of size m each to the next node. This process continues for p − 1 steps. The total size of data being transferred between nodes decreases by m words in each successive step. In every step, each node adds to its collection one m-word packet originating from a different node. Hence, in p − 1 steps, every node receives the information from all other nodes in the ensemble.

Figure 4.18. All-to-all personalized communication on a six-node ring. The label of each message is of the form {x, y}, where x is the label of the node that originally owned the message, and y is the label of the node that is the final destination of the message. The label ({x1, y1}, {x2, y2}, ..., {xn, yn}) indicates a message that is formed by concatenating n individual messages.
In the above procedure, all messages are sent in the same direction. If half of the messages are sent in one direction and the remaining half are sent in the other direction, then the communication cost due to the tw can be reduced by a factor of two. For the sake of simplicity, we ignore this constant-factor improvement.
Cost Analysis. On a ring or a bidirectional linear array, all-to-all personalized communication involves p − 1 communication steps. Since the size of the messages transferred in the i th step is m(p − i), the total time taken by this operation is
In the all-to-all personalized communication procedure described above, each node sends m(p − 1) words of data because it has an m-word packet for every other node. Assume that all messages are sent either clockwise or counterclockwise. The average distance that an m-word packet travels is ![]() , which is equal to p/2. Since there are p nodes, each performing the same type of communication, the total traffic (the total number of data words transferred between directly-connected nodes) on the network is m(p − 1) × p/2 × p. The total number of inter-node links in the network to share this load is p. Hence, the communication time for this operation is at least (tw × m(p − 1)p2/2)/p, which is equal to twm(p − 1)p/2. Disregarding the message startup time ts, this is exactly the time taken by the linear array procedure. Therefore, the all-to-all personalized communication algorithm described in this section is optimal.
, which is equal to p/2. Since there are p nodes, each performing the same type of communication, the total traffic (the total number of data words transferred between directly-connected nodes) on the network is m(p − 1) × p/2 × p. The total number of inter-node links in the network to share this load is p. Hence, the communication time for this operation is at least (tw × m(p − 1)p2/2)/p, which is equal to twm(p − 1)p/2. Disregarding the message startup time ts, this is exactly the time taken by the linear array procedure. Therefore, the all-to-all personalized communication algorithm described in this section is optimal.
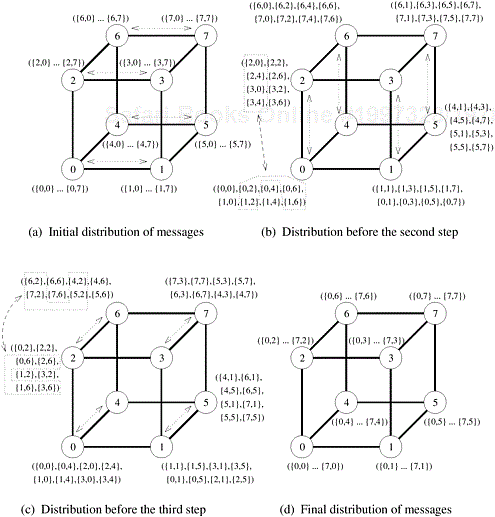
In all-to-all personalized communication on a ![]() mesh, each node first groups its p messages according to the columns of their destination nodes. Figure 4.19 shows a 3 × 3 mesh, in which every node initially has nine m-word messages, one meant for each node. Each node assembles its data into three groups of three messages each (in general,
mesh, each node first groups its p messages according to the columns of their destination nodes. Figure 4.19 shows a 3 × 3 mesh, in which every node initially has nine m-word messages, one meant for each node. Each node assembles its data into three groups of three messages each (in general, ![]() groups of
groups of ![]() messages each). The first group contains the messages destined for nodes labeled 0, 3, and 6; the second group contains the messages for nodes labeled 1, 4, and 7; and the last group has messages for nodes labeled 2, 5, and 8.
messages each). The first group contains the messages destined for nodes labeled 0, 3, and 6; the second group contains the messages for nodes labeled 1, 4, and 7; and the last group has messages for nodes labeled 2, 5, and 8.

Figure 4.19. The distribution of messages at the beginning of each phase of all-to-all personalized communication on a 3 × 3 mesh. At the end of the second phase, node i has messages ({0, i}, ..., {8, i}), where 0 ≤ i ≤ 8. The groups of nodes communicating together in each phase are enclosed in dotted boundaries.
After the messages are grouped, all-to-all personalized communication is performed independently in each row with clustered messages of size ![]() . One cluster contains the information for all
. One cluster contains the information for all ![]() nodes of a particular column. Figure 4.19(b) shows the distribution of data among the nodes at the end of this phase of communication.
nodes of a particular column. Figure 4.19(b) shows the distribution of data among the nodes at the end of this phase of communication.
Before the second communication phase, the messages in each node are sorted again, this time according to the rows of their destination nodes; then communication similar to the first phase takes place in all the columns of the mesh. By the end of this phase, each node receives a message from every other node.
Cost Analysis. We can compute the time spent in the first phase by substituting ![]() for the number of nodes, and
for the number of nodes, and ![]() for the message size in Equation 4.7. The result of this substitution is
for the message size in Equation 4.7. The result of this substitution is ![]() . The time spent in the second phase is the same as that in the first phase. Therefore, the total time for all-to-all personalized communication of messages of size m on a p-node two-dimensional square mesh is
. The time spent in the second phase is the same as that in the first phase. Therefore, the total time for all-to-all personalized communication of messages of size m on a p-node two-dimensional square mesh is
The expression for the communication time of all-to-all personalized communication in Equation 4.8 does not take into account the time required for the local rearrangement of data (that is, sorting the messages by rows or columns). Assuming that initially the data is ready for the first communication phase, the second communication phase requires the rearrangement of mp words of data. If tr is the time to perform a read and a write operation on a single word of data in a node’s local memory, then the total time spent in data rearrangement by a node during the entire procedure is trmp (Problem 4.21). This time is much smaller than the time spent by each node in communication.
An analysis along the lines of that for the linear array would show that the communication time given by Equation 4.8 for all-to-all personalized communication on a square mesh is optimal within a small constant factor (Problem 4.11).
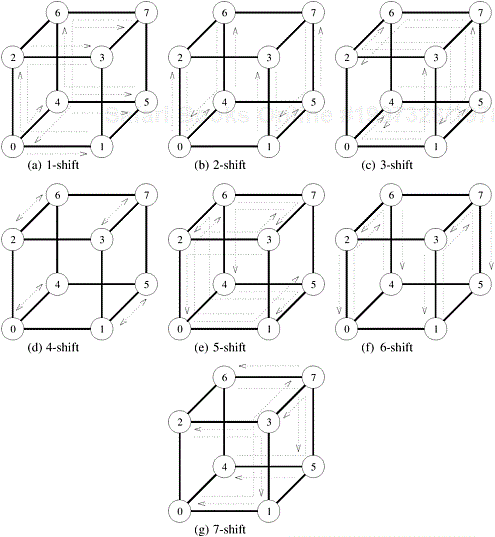
One way of performing all-to-all personalized communication on a p-node hypercube is to simply extend the two-dimensional mesh algorithm to log p dimensions. Figure 4.20 shows the communication steps required to perform this operation on a three-dimensional hypercube. As shown in the figure, communication takes place in log p steps. Pairs of nodes exchange data in a different dimension in each step. Recall that in a p-node hypercube, a set of p/2 links in the same dimension connects two subcubes of p/2 nodes each (Section 2.4.3). At any stage in all-to-all personalized communication, every node holds p packets of size m each. While communicating in a particular dimension, every node sends p/2 of these packets (consolidated as one message). The destinations of these packets are the nodes of the other subcube connected by the links in current dimension.
In the preceding procedure, a node must rearrange its messages locally before each of the log p communication steps. This is necessary to make sure that all p/2 messages destined for the same node in a communication step occupy contiguous memory locations so that they can be transmitted as a single consolidated message.
Cost Analysis. In the above hypercube algorithm for all-to-all personalized communication, mp/2 words of data are exchanged along the bidirectional channels in each of the log p iterations. The resulting total communication time is
Before each of the log p communication steps, a node rearranges mp words of data. Hence, a total time of trmp log p is spent by each node in local rearrangement of data during the entire procedure. Here tr is the time needed to perform a read and a write operation on a single word of data in a node’s local memory. For most practical computers, tr is much smaller than tw; hence, the time to perform an all-to-all personalized communication is dominated by the communication time.
Interestingly, unlike the linear array and mesh algorithms described in this section, the hypercube algorithm is not optimal. Each of the p nodes sends and receives m(p − 1) words of data and the average distance between any two nodes on a hypercube is (log p)/2. Therefore, the total data traffic on the network is p × m(p − 1) × (log p)/2. Since there is a total of (p log p)/2 links in the hypercube network, the lower bound on the all-to-all personalized communication time is

An all-to-all personalized communication effectively results in all pairs of nodes exchanging some data. On a hypercube, the best way to perform this exchange is to have every pair of nodes communicate directly with each other. Thus, each node simply performs p − 1 communication steps, exchanging m words of data with a different node in every step. A node must choose its communication partner in each step so that the hypercube links do not suffer congestion. Figure 4.21 shows one such congestion-free schedule for pairwise exchange of data in a three-dimensional hypercube. As the figure shows, in the j th communication step, node i exchanges data with node (i XOR j). For example, in part (a) of the figure (step 1), the labels of communicating partners differ in the least significant bit. In part (g) (step 7), the labels of communicating partners differ in all the bits, as the binary representation of seven is 111. In this figure, all the paths in every communication step are congestion-free, and none of the bidirectional links carry more than one message in the same direction. This is true in general for a hypercube of any dimension. If the messages are routed appropriately, a congestion-free schedule exists for the p − 1 communication steps of all-to-all personalized communication on a p-node hypercube. Recall from Section 2.4.3 that a message traveling from node i to node j on a hypercube must pass through at least l links, where l is the Hamming distance between i and j (that is, the number of nonzero bits in the binary representation of (i XOR j)). A message traveling from node i to node j traverses links in l dimensions (corresponding to the nonzero bits in the binary representation of (i XOR j)). Although the message can follow one of the several paths of length l that exist between i and j (assuming l > 1), a distinct path is obtained by sorting the dimensions along which the message travels in ascending order. According to this strategy, the first link is chosen in the dimension corresponding to the least significant nonzero bit of (i XOR j), and so on. This routing scheme is known as E-cube routing.
Algorithm 4.10 for all-to-all personalized communication on a d-dimensional hypercube is based on this strategy.
Example 4.10. A procedure to perform all-to-all personalized communication on a d-dimensional hypercube. The message Mi,j initially resides on node i and is destined for node j.
1. procedure ALL_TO_ALL_PERSONAL(d, my_id) 2. begin 3. for i := 1 to 2d − 1 do 4. begin 5. partner := my_id XOR i; 6. send Mmy_id, partner to partner; 7. receive Mpartner,my_id from partner; 8. endfor; 9. end ALL_TO_ALL_PERSONAL
Cost Analysis. E-cube routing ensures that by choosing communication pairs according to Algorithm 4.10, a communication time of ts + twm is guaranteed for a message transfer between node i and node j because there is no contention with any other message traveling in the same direction along the link between nodes i and j. The total communication time for the entire operation is
A comparison of Equations 4.9 and 4.10 shows the term associated with ts is higher for the second hypercube algorithm, while the term associated with tw is higher for the first algorithm. Therefore, for small messages, the startup time may dominate, and the first algorithm may still be useful.
Circular shift is a member of a broader class of global communication operations known as permutation. A permutation is a simultaneous, one-to-one data redistribution operation in which each node sends a packet of m words to a unique node. We define a circular q-shift as the operation in which node i sends a data packet to node (i + q) mod p in a p-node ensemble (0 < q < p). The shift operation finds application in some matrix computations and in string and image pattern matching.
The implementation of a circular q-shift is fairly intuitive on a ring or a bidirectional linear array. It can be performed by min{q , p − q} neighbor-to-neighbor communications in one direction. Mesh algorithms for circular shift can be derived by using the ring algorithm.
If the nodes of the mesh have row-major labels, a circular q-shift can be performed on a p-node square wraparound mesh in two stages. This is illustrated in Figure 4.22 for a circular 5-shift on a 4 × 4 mesh. First, the entire set of data is shifted simultaneously by (q mod ![]() ) steps along the rows. Then it is shifted by
) steps along the rows. Then it is shifted by ![]() steps along the columns. During the circular row shifts, some of the data traverse the wraparound connection from the highest to the lowest labeled nodes of the rows. All such data packets must shift an additional step forward along the columns to compensate for the
steps along the columns. During the circular row shifts, some of the data traverse the wraparound connection from the highest to the lowest labeled nodes of the rows. All such data packets must shift an additional step forward along the columns to compensate for the ![]() distance that they lost while traversing the backward edge in their respective rows. For example, the 5-shift in Figure 4.22 requires one row shift, a compensatory column shift, and finally one column shift.
distance that they lost while traversing the backward edge in their respective rows. For example, the 5-shift in Figure 4.22 requires one row shift, a compensatory column shift, and finally one column shift.
In practice, we can choose the direction of the shifts in both the rows and the columns to minimize the number of steps in a circular shift. For instance, a 3-shift on a 4 × 4 mesh can be performed by a single backward row shift. Using this strategy, the number of unit shifts in a direction cannot exceed ![]() .
.
Cost Analysis. Taking into account the compensating column shift for some packets, the total time for any circular q-shift on a p-node mesh using packets of size m has an upper bound of
In developing a hypercube algorithm for the shift operation, we map a linear array with 2d nodes onto a d-dimensional hypercube. We do this by assigning node i of the linear array to node j of the hypercube such that j is the d-bit binary reflected Gray code (RGC) of i. Figure 4.23 illustrates this mapping for eight nodes. A property of this mapping is that any two nodes at a distance of 2i on the linear array are separated by exactly two links on the hypercube. An exception is i = 0 (that is, directly-connected nodes on the linear array) when only one hypercube link separates the two nodes.
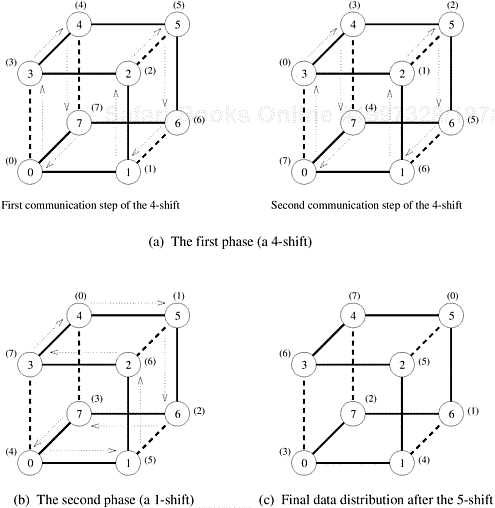
Figure 4.23. The mapping of an eight-node linear array onto a three-dimensional hypercube to perform a circular 5-shift as a combination of a 4-shift and a 1-shift.
To perform a q-shift, we expand q as a sum of distinct powers of 2. The number of terms in the sum is the same as the number of ones in the binary representation of q. For example, the number 5 can be expressed as 22 + 20. These two terms correspond to bit positions 0 and 2 in the binary representation of 5, which is 101. If q is the sum of s distinct powers of 2, then the circular q-shift on a hypercube is performed in s phases.
In each phase of communication, all data packets move closer to their respective destinations by short cutting the linear array (mapped onto the hypercube) in leaps of the powers of 2. For example, as Figure 4.23 shows, a 5-shift is performed by a 4-shift followed by a 1-shift. The number of communication phases in a q-shift is exactly equal to the number of ones in the binary representation of q. Each phase consists of two communication steps, except the 1-shift, which, if required (that is, if the least significant bit of q is 1), consists of a single step. For example, in a 5-shift, the first phase of a 4-shift (Figure 4.23(a)) consists of two steps and the second phase of a 1-shift (Figure 4.23(b)) consists of one step. Thus, the total number of steps for any q in a p-node hypercube is at most 2 log p − 1.
All communications in a given time step are congestion-free. This is ensured by the property of the linear array mapping that all nodes whose mutual distance on the linear array is a power of 2 are arranged in disjoint subarrays on the hypercube. Thus, all nodes can freely communicate in a circular fashion in their respective subarrays. This is shown in Figure 4.23(a), in which nodes labeled 0, 3, 4, and 7 form one subarray and nodes labeled 1, 2, 5, and 6 form another subarray.
The upper bound on the total communication time for any shift of m-word packets on a p-node hypercube is
We can reduce this upper bound to (ts + twm) log p by performing both forward and backward shifts. For example, on eight nodes, a 6-shift can be performed by a single backward 2-shift instead of a forward 4-shift followed by a forward 2-shift.
We now show that if the E-cube routing introduced in Section 4.5 is used, then the time for circular shift on a hypercube can be improved by almost a factor of log p for large messages. This is because with E-cube routing, each pair of nodes with a constant distance l (i ≤ l < p) has a congestion-free path (Problem 4.22) in a p-node hypercube with bidirectional channels. Figure 4.24 illustrates the non-conflicting paths of all the messages in circular q -shift operations for 1 ≤ q < 8 on an eight-node hypercube. In a circular q-shift on a p-node hypercube, the longest path contains log p − γ(q) links, where γ(q) is the highest integer j such that q is divisible by 2j (Problem 4.23). Thus, the total communication time for messages of length m is
So far in this chapter, we have derived procedures for various communication operations and their communication times under the assumptions that the original messages could not be split into smaller parts and that each node had a single port for sending and receiving data. In this section, we briefly discuss the impact of relaxing these assumptions on some of the communication operations.
In the procedures described in Sections 4.1–4.6, we assumed that an entire m-word packet of data travels between the source and the destination nodes along the same path. If we split large messages into smaller parts and then route these parts through different paths, we can sometimes utilize the communication network better. We have already shown that, with a few exceptions like one-to-all broadcast, all-to-one reduction, all-reduce, etc., the communication operations discussed in this chapter are asymptotically optimal for large messages; that is, the terms associated with tw in the costs of these operations cannot be reduced asymptotically. In this section, we present asymptotically optimal algorithms for three global communication operations.
Note that the algorithms of this section rely on m being large enough to be split into p roughly equal parts. Therefore, the earlier algorithms are still useful for shorter messages. A comparison of the cost of the algorithms in this section with those presented earlier in this chapter for the same operations would reveal that the term associated with ts increases and the term associated with tw decreases when the messages are split. Therefore, depending on the actual values of ts, tw, and p, there is a cut-off value for the message size m and only the messages longer than the cut-off would benefit from the algorithms in this section.
Consider broadcasting a single message M of size m from one source node to all the nodes in a p-node ensemble. If m is large enough so that M can be split into p parts M0, M1, ..., M p−1 of size m/p each, then a scatter operation (Section 4.4) can place Mi on node i in time ts log p + tw(m/p)(p − 1). Note that the desired result of the one-to-all broadcast is to place M = M0∪M1∪···∪Mp−1 on all nodes. This can be accomplished by an all-to-all broadcast of the messages of size m/p residing on each node after the scatter operation. This all-to-all broadcast can be completed in time ts log p + tw(m/p)(p − 1) on a hypercube. Thus, on a hypercube, one-to-all broadcast can be performed in time
Compared to Equation 4.1, this algorithm has double the startup cost, but the cost due to the tw term has been reduced by a factor of (log p)/2. Similarly, one-to-all broadcast can be improved on linear array and mesh interconnection networks as well.
All-to-one reduction is a dual of one-to-all broadcast. Therefore, an algorithm for all-to-one reduction can be obtained by reversing the direction and the sequence of communication in one-to-all broadcast. We showed above how an optimal one-to-all broadcast algorithm can be obtained by performing a scatter operation followed by an all-to-all broadcast. Therefore, using the notion of duality, we should be able to perform an all-to-one reduction by performing all-to-all reduction (dual of all-to-all broadcast) followed by a gather operation (dual of scatter). We leave the details of such an algorithm as an exercise for the reader (Problem 4.17).
Since an all-reduce operation is semantically equivalent to an all-to-one reduction followed by a one-to-all broadcast, the asymptotically optimal algorithms for these two operations presented above can be used to construct a similar algorithm for the all-reduce operation. Breaking all-to-one reduction and one-to-all broadcast into their component operations, it can be shown that an all-reduce operation can be accomplished by an all-to-all reduction followed by a gather followed by a scatter followed by an all-to-all broadcast. Since the intermediate gather and scatter would simply nullify each other’s effect, all-reduce just requires an all-to-all reduction and an all-to-all broadcast. First, the m-word messages on each of the p nodes are logically split into p components of size roughly m/p words. Then, an all-to-all reduction combines all the i th components on pi. After this step, each node is left with a distinct m/p-word component of the final result. An all-to-all broadcast can construct the concatenation of these components on each node.
A p-node hypercube interconnection network allows all-to-one reduction and one-to-all broadcast involving messages of size m/p in time ts log p + tw(m/p)(p − 1) each. Therefore, the all-reduce operation can be completed in time
In a parallel architecture, a single node may have multiple communication ports with links to other nodes in the ensemble. For example, each node in a two-dimensional wraparound mesh has four ports, and each node in a d-dimensional hypercube has d ports. In this book, we generally assume what is known as the single-port communication model. In single-port communication, a node can send data on only one of its ports at a time. Similarly, a node can receive data on only one port at a time. However, a node can send and receive data simultaneously, either on the same port or on separate ports. In contrast to the single-port model, an all-port communication model permits simultaneous communication on all the channels connected to a node.
On a p-node hypercube with all-port communication, the coefficients of tw in the expressions for the communication times of one-to-all and all-to-all broadcast and personalized communication are all smaller than their single-port counterparts by a factor of log p. Since the number of channels per node for a linear array or a mesh is constant, all-port communication does not provide any asymptotic improvement in communication time on these architectures.
Despite the apparent speedup, the all-port communication model has certain limitations. For instance, not only is it difficult to program, but it requires that the messages are large enough to be split efficiently among different channels. In several parallel algorithms, an increase in the size of messages means a corresponding increase in the granularity of computation at the nodes. When the nodes are working with large data sets, the internode communication time is dominated by the computation time if the computational complexity of the algorithm is higher than the communication complexity. For example, in the case of matrix multiplication, there are n3 computations for n2 words of data transferred among the nodes. If the communication time is a small fraction of the total parallel run time, then improving the communication by using sophisticated techniques is not very advantageous in terms of the overall run time of the parallel algorithm.
Another limitation of all-port communication is that it can be effective only if data can be fetched and stored in memory at a rate sufficient to sustain all the parallel communication. For example, to utilize all-port communication effectively on a p-node hypercube, the memory bandwidth must be greater than the communication bandwidth of a single channel by a factor of at least log p; that is, the memory bandwidth must increase with the number of nodes to support simultaneous communication on all ports. Some modern parallel computers, like the IBM SP, have a very natural solution for this problem. Each node of the distributed-memory parallel computer is a NUMA shared-memory multiprocessor. Multiple ports are then served by separate memory banks and full memory and communication bandwidth can be utilized if the buffers for sending and receiving data are placed appropriately across different memory banks.
Table 4.1 summarizes the communication times for various collective communications operations discussed in this chapter. The time for one-to-all broadcast, all-to-one reduction, and the all-reduce operations is the minimum of two expressions. This is because, depending on the message size m, either the algorithms described in Sections 4.1 and 4.3 or the ones described in Section 4.7 are faster. Table 4.1 assumes that the algorithm most suitable for the given message size is chosen. The communication-time expressions in Table 4.1 have been derived in the earlier sections of this chapter in the context of a hypercube interconnection network with cut-through routing. However, these expressions and the corresponding algorithms are valid for any architecture with a Θ(p) cross-section bandwidth (Section 2.4.4). In fact, the terms associated with tw for the expressions for all operations listed in Table 4.1, except all-to-all personalized communication and circular shift, would remain unchanged even on ring and mesh networks (or any k-d mesh network) provided that the logical processes are mapped onto the physical nodes of the network appropriately. The last column of Table 4.1 gives the asymptotic cross-section bandwidth required to perform an operation in the time given by the second column of the table, assuming an optimal mapping of processes to nodes. For large messages, only all-to-all personalized communication and circular shift require the full Θ(p) cross-section bandwidth. Therefore, as discussed in Section 2.5.1, when applying the expressions for the time of these operations on a network with a smaller cross-section bandwidth, the tw term must reflect the effective bandwidth. For example, the bisection width of a p-node square mesh is Θ![]() and that of a p-node ring is Θ(1). Therefore, while performing all-to-all personalized communication on a square mesh, the effective per-word transfer time would be Θ
and that of a p-node ring is Θ(1). Therefore, while performing all-to-all personalized communication on a square mesh, the effective per-word transfer time would be Θ![]() times the tw of individual links, and on a ring, it would be Θ(p) times the tw of individual links.
times the tw of individual links, and on a ring, it would be Θ(p) times the tw of individual links.
Table 4.1. Summary of communication times of various operations discussed in Sections 4.1–4.7 on a hypercube interconnection network. The message size for each operation is m and the number of nodes is p.
|
Operation |
Hypercube Time |
B/W Requirement |
|---|---|---|
|
One-to-all broadcast, All-to-one reduction |
min((ts + twm) log p, 2(ts log p + twm)) |
Θ(1) |
|
All-to-all broadcast, All-to-all reduction |
ts log p + twm(p − 1) |
Θ(1) |
|
All-reduce |
min((ts + twm) log p, 2(ts log p + twm)) |
Θ(1) |
|
Scatter, Gather |
ts log p + twm(p − 1) |
Θ(1) |
|
All-to-all personalized |
(ts + twm)(p − 1) |
Θ(p) |
|
Circular shift |
ts + twm |
Θ(p) |
Table 4.2. MPI names of the various operations discussed in this chapter.
|
Operation |
MPI Name |
|---|---|
|
One-to-all broadcast |
MPI_Bcast |
|
All-to-one reduction |
MPI_Reduce |
|
All-to-all broadcast |
MPI_Allgather |
|
All-to-all reduction |
MPI_Reduce_scatter |
|
All-reduce |
MPI_Allreduce |
|
Gather |
MPI_Gather |
|
Scatter |
MPI_Scatter |
|
All-to-all personalized |
MPI_Alltoall |
The collective communications operations discussed in this chapter occur frequently in many parallel algorithms. In order to facilitate speedy and portable design of efficient parallel programs, most parallel computer vendors provide pre-packaged software for performing these collective communications operations. The most commonly used standard API for these operations is known as the Message Passing Interface, or MPI. Table 4.2 gives the names of the MPI functions that correspond to the communications operations described in this chapter.
In this chapter, we studied a variety of data communication operations for the linear array, mesh, and hypercube interconnection topologies. Saad and Schultz [SS89b] discuss implementation issues for these operations on these and other architectures, such as shared-memory and a switch or bus interconnect. Most parallel computer vendors provide standard APIs for inter-process communications via message-passing. Two of the most common APIs are the message passing interface (MPI) [SOHL+96] and the parallel virtual machine (PVM) [GBD+94].
The hypercube algorithm for a certain communication operation is often the best algorithm for other less-connected architectures too, if they support cut-through routing. Due to the versatility of the hypercube architecture and the wide applicability of its algorithms, extensive work has been done on implementing various communication operations on hypercubes [BOS+91, BR90, BT97, FF86, JH89, Joh90, MdV87, RS90b, SS89a, SW87]. The properties of a hypercube network that are used in deriving the algorithms for various communication operations on it are described by Saad and Schultz [SS88].
The all-to-all personalized communication problem in particular has been analyzed for the hypercube architecture by Boppana and Raghavendra [BR90], Johnsson and Ho [JH91], Seidel [Sei89], and Take [Tak87]. E-cube routing that guarantees congestion-free communication in Algorithm 4.10 for all-to-all personalized communication is described by Nugent [Nug88].
The all-reduce and the prefix sums algorithms of Section 4.3 are described by Ranka and Sahni [RS90b]. Our discussion of the circular shift operation is adapted from Bertsekas and Tsitsiklis [BT97]. A generalized form of prefix sums, often referred to as scan, has been used by some researchers as a basic primitive in data-parallel programming. Blelloch [Ble90] defines a scan vector model, and describes how a wide variety of parallel programs can be expressed in terms of the scan primitive and its variations.
The hypercube algorithm for one-to-all broadcast using spanning binomial trees is described by Bertsekas and Tsitsiklis [BT97] and Johnsson and Ho [JH89]. In the spanning tree algorithm described in Section 4.7.1, we split the m-word message to be broadcast into log p parts of size m/log p for ease of presenting the algorithm. Johnsson and Ho [JH89] show that the optimal size of the parts is ![]() . In this case, the number of messages may be greater than log p. These smaller messages are sent from the root of the spanning binomial tree to its log p subtrees in a circular fashion. With this strategy, one-to-all broadcast on a p-node hypercube can be performed in time
. In this case, the number of messages may be greater than log p. These smaller messages are sent from the root of the spanning binomial tree to its log p subtrees in a circular fashion. With this strategy, one-to-all broadcast on a p-node hypercube can be performed in time ![]() .
.
Algorithms using the all-port communication model have been described for a variety of communication operations on the hypercube architecture by Bertsekas and Tsitsiklis [BT97], Johnsson and Ho [JH89], Ho and Johnsson [HJ87], Saad and Schultz [SS89a], and Stout and Wagar [SW87]. Johnsson and Ho [JH89] show that on a p-node hypercube with all-port communication, the coefficients of tw in the expressions for the communication times of one-to-all and all-to-all broadcast and personalized communication are all smaller than those of their single-port counterparts by a factor of log p. Gupta and Kumar [GK91] show that all-port communication may not improve the scalability of an algorithm on a parallel architecture over single-port communication.
The elementary operations described in this chapter are not the only ones used in parallel applications. A variety of other useful operations for parallel computers have been described in literature, including selection [Akl89], pointer jumping [HS86, Jaj92], BPC permutations [Joh90, RS90b], fetch-and-op [GGK+83], packing [Lev87, Sch80], bit reversal [Loa92], and keyed-scan or multi-prefix [Ble90, Ran89].
Sometimes data communication does not follow any predefined pattern, but is arbitrary, depending on the application. In such cases, a simplistic approach of routing the messages along the shortest data paths between their respective sources and destinations leads to contention and imbalanced communication. Leighton, Maggs, and Rao [LMR88], Valiant [Val82], and Valiant and Brebner [VB81] discuss efficient routing methods for arbitrary permutations of messages.
4.1 Modify Algorithms 4.1, 4.2, and 4.3 so that they work for any number of processes, not just the powers of 2.
4.2 Section 4.1 presents the recursive doubling algorithm for one-to-all broadcast, for all three networks (ring, mesh, hypercube). Note that in the hypercube algorithm of Figure 4.6, a message is sent along the highest dimension first, and then sent to lower dimensions (in Algorithm 4.1, line 4, i goes down from d − 1 to 0). The same algorithm can be used for mesh and ring and ensures that messages sent in different time steps do not interfere with each other.
Let’s now change the algorithm so that the message is sent along the lowest dimension first (i.e., in Algorithm 3.1, line 4, i goes up from 0 to d − 1). So in the first time step, processor 0 will communicate with processor 1; in the second time step, processors 0 and 1 will communicate with 2 and 3, respectively; and so on.
What is the run time of this revised algorithm on hypercube?
What is the run time of this revised algorithm on ring?
For these derivations, if k messages have to traverse the same link at the same time, then assume that the effective per-word-transfer time for these messages is ktw.
4.3 On a ring, all-to-all broadcast can be implemented in two different ways: (a) the standard ring algorithm as shown in Figure 4.9 and (b) the hypercube algorithm as shown in Figure 4.11.
What is the run time for case (a)?
What is the run time for case (b)?
If k messages have to traverse the same link at the same time, then assume that the effective per-word-transfer time for these messages is ktw. Also assume that ts = 100 × tw.
Which of the two methods, (a) or (b), above is better if the message size m is very large?
Which method is better if m is very small (may be one word)?
4.4 Write a procedure along the lines of Algorithm 4.6 for performing all-to-all reduction on a mesh.
4.5 (All-to-all broadcast on a tree) Given a balanced binary tree as shown in Figure 4.7, describe a procedure to perform all-to-all broadcast that takes time (ts + twmp/2) log p for m-word messages on p nodes. Assume that only the leaves of the tree contain nodes, and that an exchange of two m-word messages between any two nodes connected by bidirectional channels takes time ts + twmk if the communication channel (or a part of it) is shared by k simultaneous messages.
4.6 Consider the all-reduce operation in which each processor starts with an array of m words, and needs to get the global sum of the respective words in the array at each processor. This operation can be implemented on a ring using one of the following three alternatives:
All-to-all broadcast of all the arrays followed by a local computation of the sum of the respective elements of the array.
Single node accumulation of the elements of the array, followed by a one-to-all broadcast of the result array.
An algorithm that uses the pattern of the all-to-all broadcast, but simply adds numbers rather than concatenating messages.
For each of the above cases, compute the run time in terms of m, ts, and tw.
Assume that ts = 100, tw = 1, and m is very large. Which of the three alternatives (among (i), (ii) or (iii)) is better?
Assume that ts = 100, tw = 1, and m is very small (say 1). Which of the three alternatives (among (i), (ii) or (iii)) is better?
4.7 (One-to-all personalized communication on a linear array and a mesh) Give the procedures and their communication times for one-to-all personalized communication of m-word messages on p nodes for the linear array and the mesh architectures.
Hint: For the mesh, the algorithm proceeds in two phases as usual and starts with the source distributing pieces of
 words among the
words among the 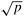 nodes in its row such that each of these nodes receives the data meant for all the
nodes in its row such that each of these nodes receives the data meant for all the 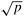 nodes in its column.
nodes in its column.4.8 (All-to-all reduction) The dual of all-to-all broadcast is all-to-all reduction, in which each node is the destination of an all-to-one reduction. For example, consider the scenario where p nodes have a vector of p elements each, and the i th node (for all i such that 0 ≤ i < p) gets the sum of the i th elements of all the vectors. Describe an algorithm to perform all-to-all reduction on a hypercube with addition as the associative operator. If each message contains m words and tadd is the time to perform one addition, how much time does your algorithm take (in terms of m, p, tadd, ts and tw)?
Hint: In all-to-all broadcast, each node starts with a single message and collects p such messages by the end of the operation. In all-to-all reduction, each node starts with p distinct messages (one meant for each node) but ends up with a single message.
4.9 Parts (c), (e), and (f) of Figure 4.21 show that for any node in a three-dimensional hypercube, there are exactly three nodes whose shortest distance from the node is two links. Derive an exact expression for the number of nodes (in terms of p and l) whose shortest distance from any given node in a p-node hypercube is l.
4.10 Give a hypercube algorithm to compute prefix sums of n numbers if p is the number of nodes and n/p is an integer greater than 1. Assuming that it takes time tadd to add two numbers and time ts to send a message of unit length between two directly-connected nodes, give an exact expression for the total time taken by the algorithm.
4.11 Show that if the message startup time ts is zero, then the expression
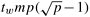 for the time taken by all-to-all personalized communication on a
for the time taken by all-to-all personalized communication on a  mesh is optimal within a small (≤ 4) constant factor.
mesh is optimal within a small (≤ 4) constant factor.4.12 Modify the linear array and the mesh algorithms in Sections 4.1–4.5 to work without the end-to-end wraparound connections. Compare the new communication times with those of the unmodified procedures. What is the maximum factor by which the time for any of the operations increases on either the linear array or the mesh?
4.13 (3-D mesh) Give optimal (within a small constant) algorithms for one-to-all and all-to-all broadcasts and personalized communications on a p1/3 × p1/3 × p1/3 three-dimensional mesh of p nodes with store-and-forward routing. Derive expressions for the total communication times of these procedures.
4.14 Assume that the cost of building a parallel computer with p nodes is proportional to the total number of communication links within it. Let the cost effectiveness of an architecture be inversely proportional to the product of the cost of a p-node ensemble of this architecture and the communication time of a certain operation on it. Assuming ts to be zero, which architecture is more cost effective for each of the operations discussed in this chapter – a standard 3-D mesh or a sparse 3-D mesh?
4.15 Repeat Problem 4.14 when ts is a nonzero constant but tw = 0. Under this model of communication, the message transfer time between two directly-connected nodes is fixed, regardless of the size of the message. Also, if two packets are combined and transmitted as one message, the communication latency is still ts.
4.16 (k-to-all broadcast) Let k-to-all broadcast be an operation in which k nodes simultaneously perform a one-to-all broadcast of m-word messages. Give an algorithm for this operation that has a total communication time of ts log p + twm(k log(p/k) + k − 1) on a p-node hypercube. Assume that the m-word messages cannot be split, k is a power of 2, and 1 ≤ k ≤ p.
4.17 Give a detailed description of an algorithm for performing all-to-one reduction in time 2(ts log p + twm(p − 1)/ p) on a p-node hypercube by splitting the original messages of size m into p nearly equal parts of size m/p each.
4.18 If messages can be split and their parts can be routed independently, then derive an algorithm for k-to-all broadcast such that its communication time is less than that of the algorithm in Problem 4.16 for a p-node hypercube.
4.19 Show that, if m ≥ p, then all-to-one reduction with message size m can be performed on a p-node hypercube spending time 2(ts log p + twm) in communication.
Hint: Express all-to-one reduction as a combination of all-to-all reduction and gather.
4.20 (k-to-all personalized communication) In k-to-all personalized communication, k nodes simultaneously perform a one-to-all personalized communication (1 ≤ k ≤ p) in a p-node ensemble with individual packets of size m. Show that, if k is a power of 2, then this operation can be performed on a hypercube in time ts (log( p/k) + k − 1) + twm(p − 1).
4.21 Assuming that it takes time tr to perform a read and a write operation on a single word of data in a node’s local memory, show that all-to-all personalized communication on a p-node mesh (Section 4.5.2) spends a total of time trmp in internal data movement on the nodes, where m is the size of an individual message.
Hint: The internal data movement is equivalent to transposing a
 array of messages of size m.
array of messages of size m.4.22 Show that in a p-node hypercube, all the p data paths in a circular q-shift are congestion-free if E-cube routing (Section 4.5) is used.
Hint: (1) If q > p/2, then a q-shift is isomorphic to a (p − q)-shift on a p-node hypercube. (2) Prove by induction on hypercube dimension. If all paths are congestion-free for a q-shift (1 ≤ q < p) on a p-node hypercube, then all these paths are congestion-free on a 2 p-node hypercube also.
4.23 Show that the length of the longest path of any message in a circular q-shift on a p-node hypercube is log p − γ(q), where γ(q) is the highest integer j such that q is divisible by 2j.
Hint: (1) If q = p/2, then γ(q) = log p − 1 on a p-node hypercube. (2) Prove by induction on hypercube dimension. For a given q, γ(q) increases by one each time the number of nodes is doubled.
4.24 Derive an expression for the parallel run time of the hypercube algorithms for one-to-all broadcast, all-to-all broadcast, one-to-all personalized communication, and all-to-all personalized communication adapted unaltered for a mesh with identical communication links (same channel width and channel rate). Compare the performance of these adaptations with that of the best mesh algorithms.
4.25 As discussed in Section 2.4.4, two common measures of the cost of a network are (1) the total number of wires in a parallel computer (which is a product of number of communication links and channel width); and (2) the bisection bandwidth. Consider a hypercube in which the channel width of each link is one, that is tw = 1. The channel width of a mesh-connected computer with equal number of nodes and identical cost is higher, and is determined by the cost metric used. Let s and s′ represent the factors by which the channel width of the mesh is increased in accordance with the two cost metrics. Derive the values of s and s′. Using these, derive the communication time of the following operations on a mesh:
One-to-all broadcast
All-to-all broadcast
One-to-all personalized communication
All-to-all personalized communication
Compare these times with the time taken by the same operations on a hypercube with equal cost.
4.26 Consider a completely-connected network of p nodes. For the four communication operations in Problem 4.25 derive an expression for the parallel run time of the hypercube algorithms on the completely-connected network. Comment on whether the added connectivity of the network yields improved performance for these operations.