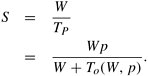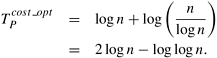A sequential algorithm is usually evaluated in terms of its execution time, expressed as a function of the size of its input. The execution time of a parallel algorithm depends not only on input size but also on the number of processing elements used, and their relative computation and interprocess communication speeds. Hence, a parallel algorithm cannot be evaluated in isolation from a parallel architecture without some loss in accuracy. A parallel system is the combination of an algorithm and the parallel architecture on which it is implemented. In this chapter, we study various metrics for evaluating the performance of parallel systems.
A number of measures of performance are intuitive. Perhaps the simplest of these is the wall-clock time taken to solve a given problem on a given parallel platform. However, as we shall see, a single figure of merit of this nature cannot be extrapolated to other problem instances or larger machine configurations. Other intuitive measures quantify the benefit of parallelism, i.e., how much faster the parallel program runs with respect to the serial program. However, this characterization suffers from other drawbacks, in addition to those mentioned above. For instance, what is the impact of using a poorer serial algorithm that is more amenable to parallel processing? For these reasons, more complex measures for extrapolating performance to larger machine configurations or problems are often necessary. With these objectives in mind, this chapter focuses on metrics for quantifying the performance of parallel programs.
Using twice as many hardware resources, one can reasonably expect a program to run twice as fast. However, in typical parallel programs, this is rarely the case, due to a variety of overheads associated with parallelism. An accurate quantification of these overheads is critical to the understanding of parallel program performance.
A typical execution profile of a parallel program is illustrated in Figure 5.1. In addition to performing essential computation (i.e., computation that would be performed by the serial program for solving the same problem instance), a parallel program may also spend time in interprocess communication, idling, and excess computation (computation not performed by the serial formulation).
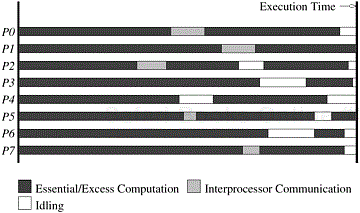
Figure 5.1. The execution profile of a hypothetical parallel program executing on eight processing elements. Profile indicates times spent performing computation (both essential and excess), communication, and idling.
Interprocess Interaction. Any nontrivial parallel system requires its processing elements to interact and communicate data (e.g., intermediate results). The time spent communicating data between processing elements is usually the most significant source of parallel processing overhead.
Idling. Processing elements in a parallel system may become idle due to many reasons such as load imbalance, synchronization, and presence of serial components in a program. In many parallel applications (for example, when task generation is dynamic), it is impossible (or at least difficult) to predict the size of the subtasks assigned to various processing elements. Hence, the problem cannot be subdivided statically among the processing elements while maintaining uniform workload. If different processing elements have different workloads, some processing elements may be idle during part of the time that others are working on the problem. In some parallel programs, processing elements must synchronize at certain points during parallel program execution. If all processing elements are not ready for synchronization at the same time, then the ones that are ready sooner will be idle until all the rest are ready. Parts of an algorithm may be unparallelizable, allowing only a single processing element to work on it. While one processing element works on the serial part, all the other processing elements must wait.
Excess Computation. The fastest known sequential algorithm for a problem may be difficult or impossible to parallelize, forcing us to use a parallel algorithm based on a poorer but easily parallelizable (that is, one with a higher degree of concurrency) sequential algorithm. The difference in computation performed by the parallel program and the best serial program is the excess computation overhead incurred by the parallel program.
A parallel algorithm based on the best serial algorithm may still perform more aggregate computation than the serial algorithm. An example of such a computation is the Fast Fourier Transform algorithm. In its serial version, the results of certain computations can be reused. However, in the parallel version, these results cannot be reused because they are generated by different processing elements. Therefore, some computations are performed multiple times on different processing elements. Chapter 13 discusses these algorithms in detail.
Since different parallel algorithms for solving the same problem incur varying overheads, it is important to quantify these overheads with a view to establishing a figure of merit for each algorithm.
It is important to study the performance of parallel programs with a view to determining the best algorithm, evaluating hardware platforms, and examining the benefits from parallelism. A number of metrics have been used based on the desired outcome of performance analysis.
The serial runtime of a program is the time elapsed between the beginning and the end of its execution on a sequential computer. The parallel runtime is the time that elapses from the moment a parallel computation starts to the moment the last processing element finishes execution. We denote the serial runtime by TS and the parallel runtime by TP.
The overheads incurred by a parallel program are encapsulated into a single expression referred to as the overhead function. We define overhead function or total overhead of a parallel system as the total time collectively spent by all the processing elements over and above that required by the fastest known sequential algorithm for solving the same problem on a single processing element. We denote the overhead function of a parallel system by the symbol To.
The total time spent in solving a problem summed over all processing elements is pTP . TS units of this time are spent performing useful work, and the remainder is overhead. Therefore, the overhead function (To) is given by
When evaluating a parallel system, we are often interested in knowing how much performance gain is achieved by parallelizing a given application over a sequential implementation. Speedup is a measure that captures the relative benefit of solving a problem in parallel. It is defined as the ratio of the time taken to solve a problem on a single processing element to the time required to solve the same problem on a parallel computer with p identical processing elements. We denote speedup by the symbol S.
Example 5.1 Adding n numbers using n processing elements
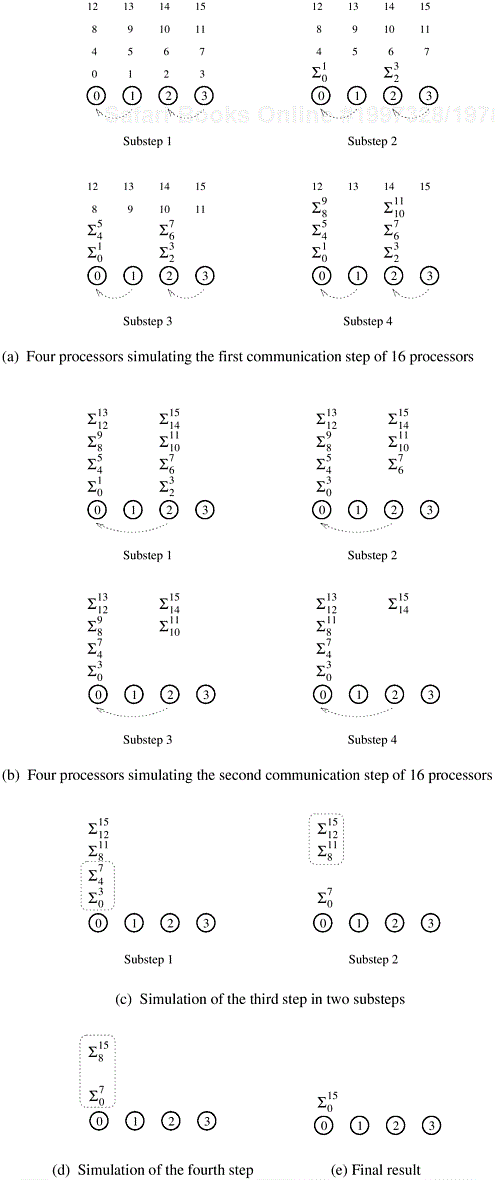
Consider the problem of adding n numbers by using n processing elements. Initially, each processing element is assigned one of the numbers to be added and, at the end of the computation, one of the processing elements stores the sum of all the numbers. Assuming that n is a power of two, we can perform this operation in log n steps by propagating partial sums up a logical binary tree of processing elements. Figure 5.2 illustrates the procedure for n = 16. The processing elements are labeled from 0 to 15. Similarly, the 16 numbers to be added are labeled from 0 to 15. The sum of the numbers with consecutive labels from i to j is denoted by ![]() .
.

Figure 5.2. Computing the globalsum of 16 partial sums using 16 processing elements. ![]() denotes the sum of numbers with consecutive labels from i to j.
denotes the sum of numbers with consecutive labels from i to j.
Each step shown in Figure 5.2 consists of one addition and the communication of a single word. The addition can be performed in some constant time, say tc, and the communication of a single word can be performed in time ts + tw. Therefore, the addition and communication operations take a constant amount of time. Thus,
Since the problem can be solved in Θ(n) time on a single processing element, its speedup is
▪
For a given problem, more than one sequential algorithm may be available, but all of these may not be equally suitable for parallelization. When a serial computer is used, it is natural to use the sequential algorithm that solves the problem in the least amount of time. Given a parallel algorithm, it is fair to judge its performance with respect to the fastest sequential algorithm for solving the same problem on a single processing element. Sometimes, the asymptotically fastest sequential algorithm to solve a problem is not known, or its runtime has a large constant that makes it impractical to implement. In such cases, we take the fastest known algorithm that would be a practical choice for a serial computer to be the best sequential algorithm. We compare the performance of a parallel algorithm to solve a problem with that of the best sequential algorithm to solve the same problem. We formally define the speedup S as the ratio of the serial runtime of the best sequential algorithm for solving a problem to the time taken by the parallel algorithm to solve the same problem on p processing elements. The p processing elements used by the parallel algorithm are assumed to be identical to the one used by the sequential algorithm.
Example 5.2 Computing speedups of parallel programs
Consider the example of parallelizing bubble sort (Section 9.3.1). Assume that a serial version of bubble sort of 105 records takes 150 seconds and a serial quicksort can sort the same list in 30 seconds. If a parallel version of bubble sort, also called odd-even sort, takes 40 seconds on four processing elements, it would appear that the parallel odd-even sort algorithm results in a speedup of 150/40 or 3.75. However, this conclusion is misleading, as in reality the parallel algorithm results in a speedup of 30/40 or 0.75 with respect to the best serial algorithm. ▪
Theoretically, speedup can never exceed the number of processing elements, p. If the best sequential algorithm takes TS units of time to solve a given problem on a single processing element, then a speedup of p can be obtained on p processing elements if none of the processing elements spends more than time TS /p. A speedup greater than p is possible only if each processing element spends less than time TS /p solving the problem. In this case, a single processing element could emulate the p processing elements and solve the problem in fewer than TS units of time. This is a contradiction because speedup, by definition, is computed with respect to the best sequential algorithm. If TS is the serial runtime of the algorithm, then the problem cannot be solved in less than time TS on a single processing element.
In practice, a speedup greater than p is sometimes observed (a phenomenon known as superlinear speedup). This usually happens when the work performed by a serial algorithm is greater than its parallel formulation or due to hardware features that put the serial implementation at a disadvantage. For example, the data for a problem might be too large to fit into the cache of a single processing element, thereby degrading its performance due to the use of slower memory elements. But when partitioned among several processing elements, the individual data-partitions would be small enough to fit into their respective processing elements’ caches. In the remainder of this book, we disregard superlinear speedup due to hierarchical memory.
Example 5.3 Superlinearity effects from caches
Consider the execution of a parallel program on a two-processor parallel system. The program attempts to solve a problem instance of size W. With this size and available cache of 64 KB on one processor, the program has a cache hit rate of 80%. Assuming the latency to cache of 2 ns and latency to DRAM of 100 ns, the effective memory access time is 2 × 0.8 + 100 × 0.2, or 21.6 ns. If the computation is memory bound and performs one FLOP/memory access, this corresponds to a processing rate of 46.3 MFLOPS. Now consider a situation when each of the two processors is effectively executing half of the problem instance (i.e., size W/2). At this problem size, the cache hit ratio is expected to be higher, since the effective problem size is smaller. Let us assume that the cache hit ratio is 90%, 8% of the remaining data comes from local DRAM, and the other 2% comes from the remote DRAM (communication overhead). Assuming that remote data access takes 400 ns, this corresponds to an overall access time of 2 × 0.9 + 100 × 0.08 + 400 × 0.02, or 17.8 ns. The corresponding execution rate at each processor is therefore 56.18, for a total execution rate of 112.36 MFLOPS. The speedup in this case is given by the increase in speed over serial formulation, i.e., 112.36/46.3 or 2.43! Here, because of increased cache hit ratio resulting from lower problem size per processor, we notice superlinear speedup. ▪
Example 5.4 Superlinearity effects due to exploratory decomposition
Consider an algorithm for exploring leaf nodes of an unstructured tree. Each leaf has a label associated with it and the objective is to find a node with a specified label, in this case ‘S’. Such computations are often used to solve combinatorial problems, where the label ‘S’ could imply the solution to the problem (Section 11.6). In Figure 5.3, we illustrate such a tree. The solution node is the rightmost leaf in the tree. A serial formulation of this problem based on depth-first tree traversal explores the entire tree, i.e., all 14 nodes. If it takes time tc to visit a node, the time for this traversal is 14tc. Now consider a parallel formulation in which the left subtree is explored by processing element 0 and the right subtree by processing element 1. If both processing elements explore the tree at the same speed, the parallel formulation explores only the shaded nodes before the solution is found. Notice that the total work done by the parallel algorithm is only nine node expansions, i.e., 9tc. The corresponding parallel time, assuming the root node expansion is serial, is 5tc (one root node expansion, followed by four node expansions by each processing element). The speedup of this two-processor execution is therefore 14tc/5tc , or 2.8!
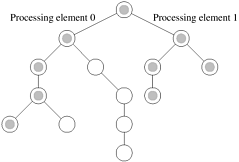
Figure 5.3. Searching an unstructured tree for a node with a given label, ‘S’, on two processing elements using depth-first traversal. The two-processor version with processor 0 searching the left subtree and processor 1 searching the right subtree expands only the shaded nodes before the solution is found. The corresponding serial formulation expands the entire tree. It is clear that the serial algorithm does more work than the parallel algorithm.
The cause for this superlinearity is that the work performed by parallel and serial algorithms is different. Indeed, if the two-processor algorithm was implemented as two processes on the same processing element, the algorithmic superlinearity would disappear for this problem instance. Note that when exploratory decomposition is used, the relative amount of work performed by serial and parallel algorithms is dependent upon the location of the solution, and it is often not possible to find a serial algorithm that is optimal for all instances. Such effects are further analyzed in greater detail in Chapter 11. ▪
Only an ideal parallel system containing p processing elements can deliver a speedup equal to p. In practice, ideal behavior is not achieved because while executing a parallel algorithm, the processing elements cannot devote 100% of their time to the computations of the algorithm. As we saw in Example 5.1, part of the time required by the processing elements to compute the sum of n numbers is spent idling (and communicating in real systems). Efficiency is a measure of the fraction of time for which a processing element is usefully employed; it is defined as the ratio of speedup to the number of processing elements. In an ideal parallel system, speedup is equal to p and efficiency is equal to one. In practice, speedup is less than p and efficiency is between zero and one, depending on the effectiveness with which the processing elements are utilized. We denote efficiency by the symbol E. Mathematically, it is given by
Example 5.5 Efficiency of adding n numbers on n processing elements
From Equation 5.3 and the preceding definition, the efficiency of the algorithm for adding n numbers on n processing elements is
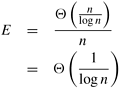
▪
We also illustrate the process of deriving the parallel runtime, speedup, and efficiency while preserving various constants associated with the parallel platform.
Example 5.6 Edge detection on images
Given an n × n pixel image, the problem of detecting edges corresponds to applying a3× 3 template to each pixel. The process of applying the template corresponds to multiplying pixel values with corresponding template values and summing across the template (a convolution operation). This process is illustrated in Figure 5.4(a) along with typical templates (Figure 5.4(b)). Since we have nine multiply-add operations for each pixel, if each multiply-add takes time tc, the entire operation takes time 9tcn2 on a serial computer.
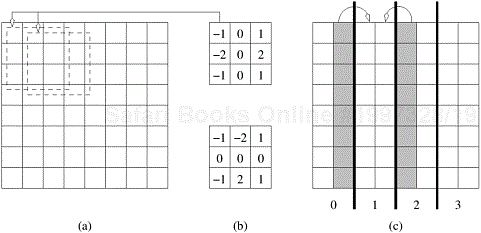
Figure 5.4. Example of edge detection: (a) an 8 × 8 image; (b) typical templates for detecting edges; and (c) partitioning of the image across four processors with shaded regions indicating image data that must be communicated from neighboring processors to processor 1.
A simple parallel algorithm for this problem partitions the image equally across the processing elements and each processing element applies the template to its own subimage. Note that for applying the template to the boundary pixels, a processing element must get data that is assigned to the adjoining processing element. Specifically, if a processing element is assigned a vertically sliced subimage of dimension n × (n/p), it must access a single layer of n pixels from the processing element to the left and a single layer of n pixels from the processing element to the right (note that one of these accesses is redundant for the two processing elements assigned the subimages at the extremities). This is illustrated in Figure 5.4(c).
On a message passing machine, the algorithm executes in two steps: (i) exchange a layer of n pixels with each of the two adjoining processing elements; and (ii) apply template on local subimage. The first step involves two n-word messages (assuming each pixel takes a word to communicate RGB data). This takes time 2(ts + twn). The second step takes time 9tcn2/p. The total time for the algorithm is therefore given by:
The corresponding values of speedup and efficiency are given by:
and

▪
We define the cost of solving a problem on a parallel system as the product of parallel runtime and the number of processing elements used. Cost reflects the sum of the time that each processing element spends solving the problem. Efficiency can also be expressed as the ratio of the execution time of the fastest known sequential algorithm for solving a problem to the cost of solving the same problem on p processing elements.
The cost of solving a problem on a single processing element is the execution time of the fastest known sequential algorithm. A parallel system is said to be cost-optimal if the cost of solving a problem on a parallel computer has the same asymptotic growth (in Θ terms) as a function of the input size as the fastest-known sequential algorithm on a single processing element. Since efficiency is the ratio of sequential cost to parallel cost, a cost-optimal parallel system has an efficiency of Θ(1).
Cost is sometimes referred to as work or processor-time product, and a cost-optimal system is also known as a pTP -optimal system.
Example 5.7 Cost of adding n numbers on n processing elements
The algorithm given in Example 5.1 for adding n numbers on n processing elements has a processor-time product of Θ(n log n). Since the serial runtime of this operation is Θ(n), the algorithm is not cost optimal. ▪
Cost optimality is a very important practical concept although it is defined in terms of asymptotics. We illustrate this using the following example.
Example 5.8 Performance of non-cost optimal algorithms
Consider a sorting algorithm that uses n processing elements to sort the list in time (log n)2. Since the serial runtime of a (comparison-based) sort is n log n, the speedup and efficiency of this algorithm are given by n/log n and 1/log n, respectively. The pTP product of this algorithm is n(log n)2. Therefore, this algorithm is not cost optimal but only by a factor of log n. Let us consider a realistic scenario in which the number of processing elements p is much less than n. An assignment of these n tasks to p < n processing elements gives us a parallel time less than n(log n)2/p. This follows from the fact that if n processing elements take time (log n)2, then one processing element would take time n(log n)2; and p processing elements would take time n(log n)2/p. The corresponding speedup of this formulation is p/log n. Consider the problem of sorting 1024 numbers (n = 1024, log n = 10) on 32 processing elements. The speedup expected is only p/log n or 3.2. This number gets worse as n increases. For n = 106, log n = 20 and the speedup is only 1.6. Clearly, there is a significant cost associated with not being cost-optimal even by a very small factor (note that a factor of log p is smaller than even ![]() ). This emphasizes the practical importance of cost-optimality. ▪
). This emphasizes the practical importance of cost-optimality. ▪
Example 5.7 illustrated an instance of an algorithm that is not cost-optimal. The algorithm discussed in this example uses as many processing elements as the number of inputs, which is excessive in terms of the number of processing elements. In practice, we assign larger pieces of input data to processing elements. This corresponds to increasing the granularity of computation on the processing elements. Using fewer than the maximum possible number of processing elements to execute a parallel algorithm is called scaling down a parallel system in terms of the number of processing elements. A naive way to scale down a parallel system is to design a parallel algorithm for one input element per processing element, and then use fewer processing elements to simulate a large number of processing elements. If there are n inputs and only p processing elements (p < n), we can use the parallel algorithm designed for n processing elements by assuming n virtual processing elements and having each of the p physical processing elements simulate n/p virtual processing elements.
As the number of processing elements decreases by a factor of n/p, the computation at each processing element increases by a factor of n/p because each processing element now performs the work of n/p processing elements. If virtual processing elements are mapped appropriately onto physical processing elements, the overall communication time does not grow by more than a factor of n/p. The total parallel runtime increases, at most, by a factor of n/p, and the processor-time product does not increase. Therefore, if a parallel system with n processing elements is cost-optimal, using p processing elements (where p < n)to simulate n processing elements preserves cost-optimality.
A drawback of this naive method of increasing computational granularity is that if a parallel system is not cost-optimal to begin with, it may still not be cost-optimal after the granularity of computation increases. This is illustrated by the following example for the problem of adding n numbers.
Example 5.9 Adding n numbers on p processing elements
Consider the problem of adding n numbers on p processing elements such that p < n and both n and p are powers of 2. We use the same algorithm as in Example 5.1 and simulate n processing elements on p processing elements. The steps leading to the solution are shown in Figure 5.5 for n = 16 and p = 4. Virtual processing element i is simulated by the physical processing element labeled i mod p; the numbers to be added are distributed similarly. The first log p of the log n steps of the original algorithm are simulated in (n/p) log p steps on p processing elements. In the remaining steps, no communication is required because the processing elements that communicate in the original algorithm are simulated by the same processing element; hence, the remaining numbers are added locally. The algorithm takes Θ((n/p) log p) time in the steps that require communication, after which a single processing element is left with n/p numbers to add, taking time Θ(n/p). Thus, the overall parallel execution time of this parallel system is Θ((n/p) log p). Consequently, its cost is Θ(n log p), which is asymptotically higher than the Θ(n) cost of adding n numbers sequentially. Therefore, the parallel system is not cost-optimal. ▪
Example 5.1 showed that n numbers can be added on an n-processor machine in time Θ(log n). When using p processing elements to simulate n virtual processing elements (p < n), the expected parallel runtime is Θ((n/p) log n). However, in Example 5.9 this task was performed in time Θ((n/p) log p) instead. The reason is that every communication step of the original algorithm does not have to be simulated; at times, communication takes place between virtual processing elements that are simulated by the same physical processing element. For these operations, there is no associated overhead. For example, the simulation of the third and fourth steps (Figure 5.5(c) and (d)) did not require any communication. However, this reduction in communication was not enough to make the algorithm cost-optimal. Example 5.10 illustrates that the same problem (adding n numbers on p processing elements) can be performed cost-optimally with a smarter assignment of data to processing elements.
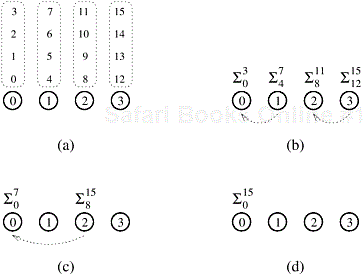
Example 5.10 Adding n numbers cost-optimally
An alternate method for adding n numbers using p processing elements is illustrated in Figure 5.6 for n = 16 and p = 4. In the first step of this algorithm, each processing element locally adds its n/p numbers in time Θ(n/p). Now the problem is reduced to adding the p partial sums on p processing elements, which can be done in time Θ(log p) by the method described in Example 5.1. The parallel runtime of this algorithm is
and its cost is Θ(n + p log p). As long as n = Ω(p log p), the cost is Θ(n), which is the same as the serial runtime. Hence, this parallel system is cost-optimal. ▪
These simple examples demonstrate that the manner in which the computation is mapped onto processing elements may determine whether a parallel system is cost-optimal. Note, however, that we cannot make all non-cost-optimal systems cost-optimal by scaling down the number of processing elements.
Very often, programs are designed and tested for smaller problems on fewer processing elements. However, the real problems these programs are intended to solve are much larger, and the machines contain larger number of processing elements. Whereas code development is simplified by using scaled-down versions of the machine and the problem, their performance and correctness (of programs) is much more difficult to establish based on scaled-down systems. In this section, we will investigate techniques for evaluating the scalability of parallel programs using analytical tools.
Example 5.11 Why is performance extrapolation so difficult?
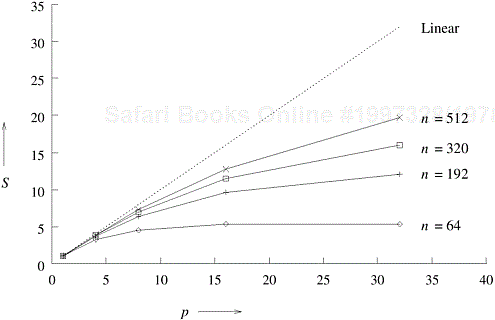
Consider three parallel algorithms for computing an n-point Fast Fourier Transform (FFT) on 64 processing elements. Figure 5.7 illustrates speedup as the value of n is increased to 18 K. Keeping the number of processing elements constant, at smaller values of n, one would infer from observed speedups that binary exchange and 3-D transpose algorithms are the best. However, as the problem is scaled up to 18 K points or more, it is evident from Figure 5.7 that the 2-D transpose algorithm yields best speedup. (These algorithms are discussed in greater detail in Chapter 13.) ▪

Figure 5.7. A comparison of the speedups obtained by the binary-exchange, 2-D transpose and 3-D transpose algorithms on 64 processing elements with tc = 2, tw = 4, ts = 25, and th = 2 (see Chapter 13 for details).
Similar results can be shown relating to the variation in number of processing elements as the problem size is held constant. Unfortunately, such parallel performance traces are the norm as opposed to the exception, making performance prediction based on limited observed data very difficult.
The efficiency of a parallel program can be written as:
Using the expression for parallel overhead (Equation 5.1), we can rewrite this expression as
The total overhead function To is an increasing function of p. This is because every program must contain some serial component. If this serial component of the program takes time tserial, then during this time all the other processing elements must be idle. This corresponds to a total overhead function of (p − 1) × tserial. Therefore, the total overhead function To grows at least linearly with p. In addition, due to communication, idling, and excess computation, this function may grow superlinearly in the number of processing elements. Equation 5.6 gives us several interesting insights into the scaling of parallel programs. First, for a given problem size (i.e. the value of TS remains constant), as we increase the number of processing elements, To increases. In such a scenario, it is clear from Equation 5.6 that the overall efficiency of the parallel program goes down. This characteristic of decreasing efficiency with increasing number of processing elements for a given problem size is common to all parallel programs.
Example 5.12 Speedup and efficiency as functions of the number of processing elements
Consider the problem of adding n numbers on p processing elements. We use the same algorithm as in Example 5.10. However, to illustrate actual speedups, we work with constants here instead of asymptotics. Assuming unit time for adding two numbers, the first phase (local summations) of the algorithm takes roughly n/p time. The second phase involves log p steps with a communication and an addition at each step. If a single communication takes unit time as well, the time for this phase is 2 log p. Therefore, we can derive parallel time, speedup, and efficiency as:
These expressions can be used to calculate the speedup and efficiency for any pair of n and p. Figure 5.8 shows the S versus p curves for a few different values of n and p. Table 5.1 shows the corresponding efficiencies.
Figure 5.8 and Table 5.1 illustrate that the speedup tends to saturate and efficiency drops as a consequence of Amdahl’s law (Problem 5.1). Furthermore, a larger instance of the same problem yields higher speedup and efficiency for the same number of processing elements, although both speedup and efficiency continue to drop with increasing p. ▪
Let us investigate the effect of increasing the problem size keeping the number of processing elements constant. We know that the total overhead function To is a function of both problem size TS and the number of processing elements p. In many cases, To grows sublinearly with respect to TS . In such cases, we can see that efficiency increases if the problem size is increased keeping the number of processing elements constant. For such algorithms, it should be possible to keep the efficiency fixed by increasing both the size of the problem and the number of processing elements simultaneously. For instance, in Table 5.1, the efficiency of adding 64 numbers using four processing elements is 0.80. If the number of processing elements is increased to 8 and the size of the problem is scaled up to add 192 numbers, the efficiency remains 0.80. Increasing p to 16 and n to 512 results in the same efficiency. This ability to maintain efficiency at a fixed value by simultaneously increasing the number of processing elements and the size of the problem is exhibited by many parallel systems. We call such systems scalable parallel systems. The scalability of a parallel system is a measure of its capacity to increase speedup in proportion to the number of processing elements. It reflects a parallel system’s ability to utilize increasing processing resources effectively.
Table 5.1. Efficiency as a function of n and p for adding n numbers on p processing elements.
|
n |
p = 1 |
p = 4 |
p = 8 |
p = 16 |
p = 32 |
|---|---|---|---|---|---|
|
64 |
1.0 |
0.80 |
0.57 |
0.33 |
0.17 |
|
192 |
1.0 |
0.92 |
0.80 |
0.60 |
0.38 |
|
320 |
1.0 |
0.95 |
0.87 |
0.71 |
0.50 |
|
512 |
1.0 |
0.97 |
0.91 |
0.80 |
0.62 |
Recall from Section 5.2.5 that a cost-optimal parallel system has an efficiency of Θ(1). Therefore, scalability and cost-optimality of parallel systems are related. A scalable parallel system can always be made cost-optimal if the number of processing elements and the size of the computation are chosen appropriately. For instance, Example 5.10 shows that the parallel system for adding n numbers on p processing elements is cost-optimal when n = Ω(p log p). Example 5.13 shows that the same parallel system is scalable if n is increased in proportion to Θ(p log p) as p is increased.
Example 5.13 Scalability of adding n numbers
For the cost-optimal addition of n numbers on p processing elements n = Ω(p log p). As shown in Table 5.1, the efficiency is 0.80 for n = 64 and p = 4. At this point, the relation between n and p is n = 8 p log p. If the number of processing elements is increased to eight, then 8 p log p = 192. Table 5.1 shows that the efficiency is indeed 0.80 with n = 192 for eight processing elements. Similarly, for p = 16, the efficiency is 0.80 for n = 8 p log p = 512. Thus, this parallel system remains cost-optimal at an efficiency of 0.80 if n is increased as 8 p log p. ▪
We summarize the discussion in the section above with the following two observations:
For a given problem size, as we increase the number of processing elements, the overall efficiency of the parallel system goes down. This phenomenon is common to all parallel systems.
In many cases, the efficiency of a parallel system increases if the problem size is increased while keeping the number of processing elements constant.
These two phenomena are illustrated in Figure 5.9(a) and (b), respectively. Following from these two observations, we define a scalable parallel system as one in which the efficiency can be kept constant as the number of processing elements is increased, provided that the problem size is also increased. It is useful to determine the rate at which the problem size must increase with respect to the number of processing elements to keep the efficiency fixed. For different parallel systems, the problem size must increase at different rates in order to maintain a fixed efficiency as the number of processing elements is increased. This rate determines the degree of scalability of the parallel system. As we shall show, a lower rate is more desirable than a higher growth rate in problem size. Let us now investigate metrics for quantitatively determining the degree of scalability of a parallel system. However, before we do that, we must define the notion of problem size precisely.

Figure 5.9. Variation of efficiency: (a) as the number of processing elements is increased for a given problem size; and (b) as the problem size is increased for a given number of processing elements. The phenomenon illustrated in graph (b) is not common to all parallel systems.
Problem Size. When analyzing parallel systems, we frequently encounter the notion of the size of the problem being solved. Thus far, we have used the term problem size informally, without giving a precise definition. A naive way to express problem size is as a parameter of the input size; for instance, n in case of a matrix operation involving n × n matrices. A drawback of this definition is that the interpretation of problem size changes from one problem to another. For example, doubling the input size results in an eight-fold increase in the execution time for matrix multiplication and a four-fold increase for matrix addition (assuming that the conventional Θ(n3) algorithm is the best matrix multiplication algorithm, and disregarding more complicated algorithms with better asymptotic complexities).
A consistent definition of the size or the magnitude of the problem should be such that, regardless of the problem, doubling the problem size always means performing twice the amount of computation. Therefore, we choose to express problem size in terms of the total number of basic operations required to solve the problem. By this definition, the problem size is Θ(n3) for n × n matrix multiplication (assuming the conventional algorithm) and Θ(n2) for n × n matrix addition. In order to keep it unique for a given problem, we define problem size as the number of basic computation steps in the best sequential algorithm to solve the problem on a single processing element, where the best sequential algorithm is defined as in Section 5.2.3. Because it is defined in terms of sequential time complexity, the problem size is a function of the size of the input. The symbol we use to denote problem size is W.
In the remainder of this chapter, we assume that it takes unit time to perform one basic computation step of an algorithm. This assumption does not impact the analysis of any parallel system because the other hardware-related constants, such as message startup time, per-word transfer time, and per-hop time, can be normalized with respect to the time taken by a basic computation step. With this assumption, the problem size W is equal to the serial runtime TS of the fastest known algorithm to solve the problem on a sequential computer.
Parallel execution time can be expressed as a function of problem size, overhead function, and the number of processing elements. We can write parallel runtime as:
The resulting expression for speedup is
Finally, we write the expression for efficiency as
In Equation 5.12, if the problem size is kept constant and p is increased, the efficiency decreases because the total overhead To increases with p. If W is increased keeping the number of processing elements fixed, then for scalable parallel systems, the efficiency increases. This is because To grows slower than Θ(W) for a fixed p. For these parallel systems, efficiency can be maintained at a desired value (between 0 and 1) for increasing p, provided W is also increased.
For different parallel systems, W must be increased at different rates with respect to p in order to maintain a fixed efficiency. For instance, in some cases, W might need to grow as an exponential function of p to keep the efficiency from dropping as p increases. Such parallel systems are poorly scalable. The reason is that on these parallel systems it is difficult to obtain good speedups for a large number of processing elements unless the problem size is enormous. On the other hand, if W needs to grow only linearly with respect to p, then the parallel system is highly scalable. That is because it can easily deliver speedups proportional to the number of processing elements for reasonable problem sizes.
For scalable parallel systems, efficiency can be maintained at a fixed value (between 0 and 1) if the ratio To/W in Equation 5.12 is maintained at a constant value. For a desired value E of efficiency,
Let K = E/(1 − E) be a constant depending on the efficiency to be maintained. Since To is a function of W and p, Equation 5.13 can be rewritten as
From Equation 5.14, the problem size W can usually be obtained as a function of p by algebraic manipulations. This function dictates the growth rate of W required to keep the efficiency fixed as p increases. We call this function the isoefficiency function of the parallel system. The isoefficiency function determines the ease with which a parallel system can maintain a constant efficiency and hence achieve speedups increasing in proportion to the number of processing elements. A small isoefficiency function means that small increments in the problem size are sufficient for the efficient utilization of an increasing number of processing elements, indicating that the parallel system is highly scalable. However, a large isoefficiency function indicates a poorly scalable parallel system. The isoefficiency function does not exist for unscalable parallel systems, because in such systems the efficiency cannot be kept at any constant value as p increases, no matter how fast the problem size is increased.
Example 5.14 Isoefficiency function of adding numbers
The overhead function for the problem of adding n numbers on p processing elements is approximately 2 p log p, as given by Equations 5.9 and 5.1. Substituting To by 2 p log p in Equation 5.14, we get
Thus, the asymptotic isoefficiency function for this parallel system is Θ(p log p). This means that, if the number of processing elements is increased from p to p′, the problem size (in this case, n) must be increased by a factor of (p′ log p′)/(p log p) to get the same efficiency as on p processing elements. In other words, increasing the number of processing elements by a factor of p′/p requires that n be increased by a factor of (p′ log p′)/(p log p) to increase the speedup by a factor of p′/p. ▪
In the simple example of adding n numbers, the overhead due to communication (hereafter referred to as the communication overhead) is a function of p only. In general, communication overhead can depend on both the problem size and the number of processing elements. A typical overhead function can have several distinct terms of different orders of magnitude with respect to p and W. In such a case, it can be cumbersome (or even impossible) to obtain the isoefficiency function as a closed function of p. For example, consider a hypothetical parallel system for which To = p3/2 + p3/4 W 3/4. For this overhead function, Equation 5.14 can be rewritten as W = Kp3/2 + Kp3/4 W 3/4. It is hard to solve this equation for W in terms of p.
Recall that the condition for constant efficiency is that the ratio To/W remains fixed. As p and W increase, the efficiency is nondecreasing as long as none of the terms of To grow faster than W. If To has multiple terms, we balance W against each term of To and compute the respective isoefficiency functions for individual terms. The component of To that requires the problem size to grow at the highest rate with respect to p determines the overall asymptotic isoefficiency function of the parallel system. Example 5.15 further illustrates this technique of isoefficiency analysis.
Example 5.15 Isoefficiency function of a parallel system with a complex overhead function
Consider a parallel system for which To = p3/2 + p3/4 W 3/4. Using only the first term of To in Equation 5.14, we get
Using only the second term, Equation 5.14 yields the following relation between W and p:
To ensure that the efficiency does not decrease as the number of processing elements increases, the first and second terms of the overhead function require the problem size to grow as Θ(p3/2) and Θ(p3), respectively. The asymptotically higher of the two rates, Θ(p3), gives the overall asymptotic isoefficiency function of this parallel system, since it subsumes the rate dictated by the other term. The reader may indeed verify that if the problem size is increased at this rate, the efficiency is Θ(1) and that any rate lower than this causes the efficiency to fall with increasing p. ▪
In a single expression, the isoefficiency function captures the characteristics of a parallel algorithm as well as the parallel architecture on which it is implemented. After performing isoefficiency analysis, we can test the performance of a parallel program on a few processing elements and then predict its performance on a larger number of processing elements. However, the utility of isoefficiency analysis is not limited to predicting the impact on performance of an increasing number of processing elements. Section 5.4.5 shows how the isoefficiency function characterizes the amount of parallelism inherent in a parallel algorithm. We will see in Chapter 13 that isoefficiency analysis can also be used to study the behavior of a parallel system with respect to changes in hardware parameters such as the speed of processing elements and communication channels. Chapter 11 illustrates how isoefficiency analysis can be used even for parallel algorithms for which we cannot derive a value of parallel runtime.
In Section 5.2.5, we stated that a parallel system is cost-optimal if the product of the number of processing elements and the parallel execution time is proportional to the execution time of the fastest known sequential algorithm on a single processing element. In other words, a parallel system is cost-optimal if and only if
Substituting the expression for TP from the right-hand side of Equation 5.10, we get the following:
Equations 5.19 and 5.20 suggest that a parallel system is cost-optimal if and only if its overhead function does not asymptotically exceed the problem size. This is very similar to the condition given by Equation 5.14 for maintaining a fixed efficiency while increasing the number of processing elements in a parallel system. If Equation 5.14 yields an isoefficiency function f(p), then it follows from Equation 5.20 that the relation W = Ω(f(p)) must be satisfied to ensure the cost-optimality of a parallel system as it is scaled up. The following example further illustrates the relationship between cost-optimality and the isoefficiency function.
Example 5.16 Relationship between cost-optimality and isoefficiency
Consider the cost-optimal solution to the problem of adding n numbers on p processing elements, presented in Example 5.10. For this parallel system, W ≈ n, and To = Θ(p log p). From Equation 5.14, its isoefficiency function is Θ(p log p); that is, the problem size must increase as Θ(p log p) to maintain a constant efficiency. In Example 5.10 we also derived the condition for cost-optimality as W = Ω(p log p). ▪
We discussed earlier that a smaller isoefficiency function indicates higher scalability. Accordingly, an ideally-scalable parallel system must have the lowest possible isoefficiency function. For a problem consisting of W units of work, no more than W processing elements can be used cost-optimally; additional processing elements will be idle. If the problem size grows at a rate slower than Θ(p) as the number of processing elements increases, then the number of processing elements will eventually exceed W. Even for an ideal parallel system with no communication, or other overhead, the efficiency will drop because processing elements added beyond p = W will be idle. Thus, asymptotically, the problem size must increase at least as fast as Θ(p) to maintain fixed efficiency; hence, Ω(p) is the asymptotic lower bound on the isoefficiency function. It follows that the isoefficiency function of an ideally scalable parallel system is Θ(p).
A lower bound of Ω(p) is imposed on the isoefficiency function of a parallel system by the number of operations that can be performed concurrently. The maximum number of tasks that can be executed simultaneously at any time in a parallel algorithm is called its degree of concurrency. The degree of concurrency is a measure of the number of operations that an algorithm can perform in parallel for a problem of size W; it is independent of the parallel architecture. If C(W) is the degree of concurrency of a parallel algorithm, then for a problem of size W, no more than C(W) processing elements can be employed effectively.
Example 5.17 Effect of concurrency on isoefficiency function
Consider solving a system of n equations in n variables by using Gaussian elimination (Section 8.3.1). The total amount of computation is Θ(n3). But then variables must be eliminated one after the other, and eliminating each variable requires Θ(n2) computations. Thus, at most Θ(n2) processing elements can be kept busy at any time. Since W = Θ(n3) for this problem, the degree of concurrency C(W) is Θ(W2/3) and at most Θ(W2/3) processing elements can be used efficiently. On the other hand, given p processing elements, the problem size should be at least Ω(p3/2) to use them all. Thus, the isoefficiency function of this computation due to concurrency is Θ(p3/2). ▪
The isoefficiency function due to concurrency is optimal (that is, Θ(p)) only if the degree of concurrency of the parallel algorithm is Θ(W). If the degree of concurrency of an algorithm is less than Θ(W), then the isoefficiency function due to concurrency is worse (that is, greater) than Θ(p). In such cases, the overall isoefficiency function of a parallel system is given by the maximum of the isoefficiency functions due to concurrency, communication, and other overheads.
We are often interested in knowing how fast a problem can be solved, or what the minimum possible execution time of a parallel algorithm is, provided that the number of processing elements is not a constraint. As we increase the number of processing elements for a given problem size, either the parallel runtime continues to decrease and asymptotically approaches a minimum value, or it starts rising after attaining a minimum value (Problem 5.12). We can determine the minimum parallel runtime ![]() for a given W by differentiating the expression for TP with respect to p and equating the derivative to zero (assuming that the function TP (W, p) is differentiable with respect to p). The number of processing elements for which TP is minimum is determined by the following equation:
for a given W by differentiating the expression for TP with respect to p and equating the derivative to zero (assuming that the function TP (W, p) is differentiable with respect to p). The number of processing elements for which TP is minimum is determined by the following equation:
Let p0 be the value of the number of processing elements that satisfies Equation 5.21. The value of ![]() can be determined by substituting p0 for p in the expression for TP . In the following example, we derive the expression for
can be determined by substituting p0 for p in the expression for TP . In the following example, we derive the expression for ![]() for the problem of adding n numbers.
for the problem of adding n numbers.
Example 5.18 Minimum execution time for adding n numbers
Under the assumptions of Example 5.12, the parallel run time for the problem of adding n numbers on p processing elements can be approximated by
Equating the derivative with respect to p of the right-hand side of Equation 5.22 to zero we get the solutions for p as follows:
Substituting p = n/2 in Equation 5.22, we get
▪
In Example 5.18, the processor-time product for p = p0 is Θ(n log n), which is higher than the Θ(n) serial complexity of the problem. Hence, the parallel system is not cost-optimal for the value of p that yields minimum parallel runtime. We now derive an important result that gives a lower bound on parallel runtime if the problem is solved cost-optimally.
Let ![]() be the minimum time in which a problem can be solved by a cost-optimal parallel system. From the discussion regarding the equivalence of cost-optimality and the isoefficiency function in Section 5.4.3, we conclude that if the isoefficiency function of a parallel system is Θ(f(p)), then a problem of size W can be solved cost-optimally if and only if W = Ω(f(p)). In other words, given a problem of size W, a cost-optimal solution requires that p = O(f−1(W)). Since the parallel runtime is Θ(W/p) for a cost-optimal parallel system (Equation 5.18), the lower bound on the parallel runtime for solving a problem of size W cost-optimally is
be the minimum time in which a problem can be solved by a cost-optimal parallel system. From the discussion regarding the equivalence of cost-optimality and the isoefficiency function in Section 5.4.3, we conclude that if the isoefficiency function of a parallel system is Θ(f(p)), then a problem of size W can be solved cost-optimally if and only if W = Ω(f(p)). In other words, given a problem of size W, a cost-optimal solution requires that p = O(f−1(W)). Since the parallel runtime is Θ(W/p) for a cost-optimal parallel system (Equation 5.18), the lower bound on the parallel runtime for solving a problem of size W cost-optimally is
Example 5.19 Minimum cost-optimal execution time for adding n numbers
As derived in Example 5.14, the isoefficiency function f(p) of this parallel system is Θ(p log p). If W = n = f(p) = p log p, then log n = log p + log log p. Ignoring the double logarithmic term, log n ≈ log p. If n = f (p) = p log p, then p = f−1(n) = n/log p ≈ n/log n. Hence, f−1(W) = Θ(n/log n). As a consequence of the relation between cost-optimality and the isoefficiency function, the maximum number of processing elements that can be used to solve this problem cost-optimally is Θ(n/log n). Using p = n/log n in Equation 5.2, we get
▪
It is interesting to observe that both ![]() and
and ![]() for adding n numbers are Θ(log n) (Equations 5.24 and 5.26). Thus, for this problem, a cost-optimal solution is also the asymptotically fastest solution. The parallel execution time cannot be reduced asymptotically by using a value of p greater than that suggested by the isoefficiency function for a given problem size (due to the equivalence between cost-optimality and the isoefficiency function). This is not true for parallel systems in general, however, and it is quite possible that
for adding n numbers are Θ(log n) (Equations 5.24 and 5.26). Thus, for this problem, a cost-optimal solution is also the asymptotically fastest solution. The parallel execution time cannot be reduced asymptotically by using a value of p greater than that suggested by the isoefficiency function for a given problem size (due to the equivalence between cost-optimality and the isoefficiency function). This is not true for parallel systems in general, however, and it is quite possible that ![]() . The following example illustrates such a parallel system.
. The following example illustrates such a parallel system.
Example 5.20 A parallel system with 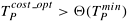
Consider the hypothetical parallel system of Example 5.15, for which
From Equation 5.10, the parallel runtime for this system is
Using the methodology of Example 5.18,

From the preceding analysis, p0 = Θ(W). Substituting p by the value of p0 in Equation 5.28, we get
According to Example 5.15, the overall isoefficiency function for this parallel system is Θ(p3), which implies that the maximum number of processing elements that can be used cost-optimally is Θ(W1/3). Substituting p = Θ(W1/3) in Equation 5.28, we get
A comparison of Equations 5.29 and 5.30 shows that ![]() is asymptotically greater than
is asymptotically greater than ![]() . ▪
. ▪
In this section, we have seen examples of both types of parallel systems: those for which ![]() is asymptotically equal to
is asymptotically equal to ![]() , and those for which
, and those for which ![]() is asymptotically greater than
is asymptotically greater than ![]() . Most parallel systems presented in this book are of the first type. Parallel systems for which the runtime can be reduced by an order of magnitude by using an asymptotically higher number of processing elements than indicated by the isoefficiency function are rare.
. Most parallel systems presented in this book are of the first type. Parallel systems for which the runtime can be reduced by an order of magnitude by using an asymptotically higher number of processing elements than indicated by the isoefficiency function are rare.
While deriving the minimum execution time for any parallel system, it is important to be aware that the maximum number of processing elements that can be utilized is bounded by the degree of concurrency C(W) of the parallel algorithm. It is quite possible that p0 is greater than C(W) for a parallel system (Problems 5.13 and 5.14). In such cases, the value of p0 is meaningless, and ![]() is given by
is given by
At this point, we have accumulated an arsenal of powerful tools for quantifying the performance and scalability of an algorithm. Let us illustrate the use of these tools for evaluating a set of parallel programs for solving a given problem. Often, we ignore constants and concern ourselves with the asymptotic behavior of quantities. In many cases, this can yield a clearer picture of relative merits and demerits of various parallel programs.
Table 5.2. Comparison of four different algorithms for sorting a given list of numbers. The table shows number of processing elements, parallel runtime, speedup, efficiency and the pTP product.
|
Algorithm |
A1 |
A2 |
A3 |
A4 |
|---|---|---|---|---|
|
p |
n2 |
log n |
n |
|
|
TP |
1 |
n |
|
|
|
S |
n log n |
log n |
|
|
|
E |
|
1 |
|
1 |
|
pTP |
n2 |
n log n |
n1.5 |
n log n |
Consider the problem of sorting a list of n numbers. The fastest serial programs for this problem run in time O (n log n). Let us look at four different parallel algorithms A1, A2, A3, and A4, for sorting a given list. The parallel runtime of the four algorithms along with the number of processing elements they can use is given in Table 5.2. The objective of this exercise is to determine which of these four algorithms is the best. Perhaps the simplest metric is one of speed; the algorithm with the lowest TP is the best. By this metric, algorithm A1 is the best, followed by A3, A4, and A2. This is also reflected in the fact that the speedups of the set of algorithms are also in this order.
However, in practical situations, we will rarely have n2 processing elements as are required by algorithm A1. Furthermore, resource utilization is an important aspect of practical program design. So let us look at how efficient each of these algorithms are. This metric of evaluating the algorithm presents a starkly different image. Algorithms A2 and A4 are the best, followed by A3 and A1. The last row of Table 5.2 presents the cost of the four algorithms. From this row, it is evident that the costs of algorithms A1 and A3 are higher than the serial runtime of n log n and therefore neither of these algorithms is cost optimal. However, algorithms A2 and A4 are cost optimal.
This set of algorithms illustrate that it is important to first understand the objectives of parallel algorithm analysis and to use appropriate metrics. This is because use of different metrics may often result in contradictory outcomes.
A number of other metrics of scalability of parallel systems have been proposed. These metrics are specifically suited to different system requirements. For example, in real time applications, the objective is to scale up a system to accomplish a task in a specified time bound. One such application is multimedia decompression, where MPEG streams must be decompressed at the rate of 25 frames/second. Consequently, a parallel system must decode a single frame in 40 ms (or with buffering, at an average of 1 frame in 40 ms over the buffered frames). Other such applications arise in real-time control, where a control vector must be generated in real-time. Several scalability metrics consider constraints on physical architectures. In many applications, the maximum size of a problem is constrained not by time, efficiency, or underlying models, but by the memory available on the machine. In such cases, metrics make assumptions on the growth function of available memory (with number of processing elements) and estimate how the performance of the parallel system changes with such scaling. In this section, we examine some of the related metrics and how they can be used in various parallel applications.
Scaled Speedup. This metric is defined as the speedup obtained when the problem size is increased linearly with the number of processing elements. If the scaled-speedup curve is close to linear with respect to the number of processing elements, then the parallel system is considered scalable. This metric is related to isoefficiency if the parallel algorithm under consideration has linear or near-linear isoefficiency function. In this case the scaled-speedup metric provides results very close to those of isoefficiency analysis, and the scaled-speedup is linear or near-linear with respect to the number of processing elements. For parallel systems with much worse isoefficiencies, the results provided by the two metrics may be quite different. In this case, the scaled-speedup versus number of processing elements curve is sublinear.
Two generalized notions of scaled speedup have been examined. They differ in the methods by which the problem size is scaled up with the number of processing elements. In one method, the size of the problem is increased to fill the available memory on the parallel computer. The assumption here is that aggregate memory of the system increases with the number of processing elements. In the other method, the size of the problem grows with p subject to an upper-bound on execution time.
Example 5.21 Memory and time-constrained scaled speedup for matrix-vector products
The serial runtime of multiplying a matrix of dimension n × n with a vector is tcn2, where tc is the time for a single multiply-add operation. The corresponding parallel runtime using a simple parallel algorithm is given by:
and the speedup S is given by:
The total memory requirement of the algorithm is Θ(n2). Let us consider the two cases of problem scaling. In the case of memory constrained scaling, we assume that the memory of the parallel system grows linearly with the number of processing elements, i.e., m = Θ(p). This is a reasonable assumption for most current parallel platforms. Since m = Θ(n2), we have n2 = c × p, for some constant c. Therefore, the scaled speedup S′ is given by:
or
In the limiting case, ![]() .
.
In the case of time constrained scaling, we have TP = O(n2/p). Since this is constrained to be constant, n2 = O(p). We notice that this case is identical to the memory constrained case. This happened because the memory and runtime of the algorithm are asymptotically identical. ▪
Example 5.22 Memory and time-constrained scaled speedup for matrix-matrix products
The serial runtime of multiplying two matrices of dimension n × n is tcn3, where tc, as before, is the time for a single multiply-add operation. The corresponding parallel runtime using a simple parallel algorithm is given by:
and the speedup S is given by:
The total memory requirement of the algorithm is Θ(n2). Let us consider the two cases of problem scaling. In the case of memory constrained scaling, as before, we assume that the memory of the parallel system grows linearly with the number of processing elements, i.e., m = Θ(p). Since m = Θ(n2), we have n2 = c × p, for some constant c. Therefore, the scaled speedup S′ is given by:

In the case of time constrained scaling, we have TP = O(n3/p). Since this is constrained to be constant, n3 = O(p), or n3 = c × p (for some constant c).
Therefore, the time-constrained speedup S″ is given by:
This example illustrates that memory-constrained scaling yields linear speedup, whereas time-constrained speedup yields sublinear speedup in the case of matrix multiplication. ▪
Serial Fraction f. The experimentally determined serial fraction f can be used to quantify the performance of a parallel system on a fixed-size problem. Consider a case when the serial runtime of a computation can be divided into a totally parallel and a totally serial component, i.e.,
Here, Tser and Tpar correspond to totally serial and totally parallel components. From this, we can write:
Here, we have assumed that all of the other parallel overheads such as excess computation and communication are captured in the serial component Tser. From these equations, it follows that:
The serial fraction f of a parallel program is defined as:
Therefore, from Equation 5.34, we have:
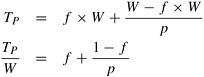
Since S = W/TP , we have
Solving for f , we get:
It is easy to see that smaller values of f are better since they result in higher efficiencies. If f increases with the number of processing elements, then it is considered as an indicator of rising communication overhead, and thus an indicator of poor scalability.
Example 5.23 Serial component of the matrix-vector product
From Equations 5.35 and 5.32, we have
Simplifying the above expression, we get

It is useful to note that the denominator of this equation is the serial runtime of the algorithm and the numerator corresponds to the overhead in parallel execution. ▪
In addition to these metrics, a number of other metrics of performance have been proposed in the literature. We refer interested readers to the bibliography for references to these.
To use today’s massively parallel computers effectively, larger problems must be solved as more processing elements are added. However, when the problem size is fixed, the objective is to attain the best compromise between efficiency and parallel runtime. Performance issues for fixed-size problems have been addressed by several researchers [FK89, GK93a, KF90, NW88, TL90, Wor90]. In most situations, additional computing power derived from increasing the number of processing elements can be used to solve bigger problems. In some situations, however, different ways of increasing the problem size may apply, and a variety of constraints may guide the scaling up of the workload with respect to the number of processing elements [SHG93]. Time-constrained scaling and memory-constrained scaling have been explored by Gustafson et al. [GMB88, Gus88, Gus92], Sun and Ni [SN90, SN93], and Worley [Wor90, Wor88, Wor91] (Problem 5.9).
An important scenario is one in which we want to make the most efficient use of the parallel system; in other words, we want the overall performance of the parallel system to increase linearly with p. This is possible only for scalable parallel systems, which are exactly those for which a fixed efficiency can be maintained for arbitrarily large p by simply increasing the problem size. For such systems, it is natural to use the isoefficiency function or related metrics [GGK93, CD87, KR87b, KRS88]. Isoefficiency analysis has been found to be very useful in characterizing the scalability of a variety of parallel algorithms [GK91, GK93b, GKS92, HX98, KN91, KR87b, KR89, KS91b, RS90b, SKAT91b, TL90, WS89, WS91]. Gupta and Kumar [GK93a, KG94] have demonstrated the relevance of the isoefficiency function in the fixed time case as well. They have shown that if the isoefficiency function is greater than Θ(p), then the problem size cannot be increased indefinitely while maintaining a fixed execution time, no matter how many processing elements are used. A number of other researchers have analyzed the performance of parallel systems with concern for overall efficiency [EZL89, FK89, MS88, NW88, TL90, Zho89, ZRV89].
Kruskal, Rudolph, and Snir [KRS88] define the concept of parallel efficient (PE) problems. Their definition is related to the concept of isoefficiency function. Problems in the class PE have algorithms with a polynomial isoefficiency function at some efficiency. The class PE makes an important distinction between algorithms with polynomial isoefficiency functions and those with worse isoefficiency functions. Kruskal et al. proved the invariance of the class PE over a variety of parallel computational models and interconnection schemes. An important consequence of this result is that an algorithm with a polynomial isoefficiency on one architecture will have a polynomial isoefficiency on many other architectures as well. There can be exceptions, however; for instance, Gupta and Kumar [GK93b] show that the fast Fourier transform algorithm has a polynomial isoefficiency on a hypercube but an exponential isoefficiency on a mesh.
Vitter and Simons [VS86] define a class of problems called PC*. PC* includes problems with efficient parallel algorithms on a PRAM. A problem in class P (the polynomial-time class) is in PC* if it has a parallel algorithm on a PRAM that can use a polynomial (in terms of input size) number of processing elements and achieve a minimal efficiency ∊. Any problem in PC* has at least one parallel algorithm such that, for an efficiency ∊, its isoefficiency function exists and is a polynomial.
A discussion of various scalability and performance measures can be found in the survey by Kumar and Gupta [KG94]. Besides the ones cited so far, a number of other metrics of performance and scalability of parallel systems have been proposed [BW89, CR89, CR91, Fla90, Hil90, Kun86, Mol87, MR, NA91, SG91, SR91, SZ96, VC89].
Flatt and Kennedy [FK89, Fla90] show that if the overhead function satisfies certain mathematical properties, then there exists a unique value p0 of the number of processing elements for which TP is minimum for a given W. A property of To on which their analysis depends heavily is that To > Θ(p). Gupta and Kumar [GK93a] show that there exist parallel systems that do not obey this condition, and in such cases the point of peak performance is determined by the degree of concurrency of the algorithm being used.
Marinescu and Rice [MR] develop a model to describe and analyze a parallel computation on an MIMD computer in terms of the number of threads of control p into which the computation is divided and the number of events g(p) as a function of p. They consider the case where each event is of a fixed duration θ and hence To = θg(p). Under these assumptions on To, they conclude that with increasing number of processing elements, the speedup saturates at some value if To = Θ(p), and it asymptotically approaches zero if To = Θ(pm),where m ≥ 2. Gupta and Kumar [GK93a] generalize these results for a wider class of overhead functions. They show that the speedup saturates at some maximum value if To ≤ Θ(p), and the speedup attains a maximum value and then drops monotonically with p if To > Θ(p).
Eager et al. [EZL89] and Tang and Li [TL90] have proposed a criterion of optimality of a parallel system so that a balance is struck between efficiency and speedup. They propose that a good choice of operating point on the execution time versus efficiency curve is that where the incremental benefit of adding processing elements is roughly ![]() per processing element or, in other words, efficiency is 0.5. They conclude that for To = Θ(p), this is also equivalent to operating at a point where the ES product is maximum or p(TP)2 is minimum. This conclusion is a special case of the more general case presented by Gupta and Kumar [GK93a].
per processing element or, in other words, efficiency is 0.5. They conclude that for To = Θ(p), this is also equivalent to operating at a point where the ES product is maximum or p(TP)2 is minimum. This conclusion is a special case of the more general case presented by Gupta and Kumar [GK93a].
Belkhale and Banerjee [BB90], Leuze et al. [LDP89], Ma and Shea [MS88], and Park and Dowdy [PD89] address the important problem of optimal partitioning of the processing elements of a parallel computer among several applications of different scalabilities executing simultaneously.
5.1 (Amdahl’s law [Amd67]) If a problem of size W has a serial component WS, prove that W/WS is an upper bound on its speedup, no matter how many processing elements are used.
5.2 (Superlinear speedup) Consider the search tree shown in Figure 5.10(a), in which the dark node represents the solution.
If a sequential search of the tree is performed using the standard depth-first search (DFS) algorithm (Section 11.2.1), how much time does it take to find the solution if traversing each arc of the tree takes one unit of time?
Assume that the tree is partitioned between two processing elements that are assigned to do the search job, as shown in Figure 5.10(b). If both processing elements perform a DFS on their respective halves of the tree, how much time does it take for the solution to be found? What is the speedup? Is there a speedup anomaly? If so, can you explain the anomaly?
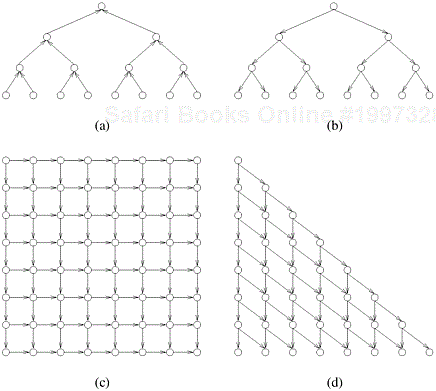
5.3 (The DAG model of parallel computation) Parallel algorithms can often be represented by dependency graphs. Four such dependency graphs are shown in Figure 5.11. If a program can be broken into several tasks, then each node of the graph represents one task. The directed edges of the graph represent the dependencies between the tasks or the order in which they must be performed to yield correct results. A node of the dependency graph can be scheduled for execution as soon as the tasks at all the nodes that have incoming edges to that node have finished execution. For example, in Figure 5.11(b), the nodes on the second level from the root can begin execution only after the task at the root is finished. Any deadlock-free dependency graph must be a directed acyclic graph (DAG); that is, it is devoid of any cycles. All the nodes that are scheduled for execution can be worked on in parallel provided enough processing elements are available. If N is the number of nodes in a graph, and n is an integer, then N = 2n − 1 for graphs (a) and (b), N = n2 for graph (c), and N = n(n + 1)/2 for graph (d) (graphs (a) and (b) are drawn for n = 4 and graphs (c) and (d) are drawn for n = 8). Assuming that each task takes one unit of time and that interprocessor communication time is zero, for the algorithms represented by each of these graphs:
Compute the degree of concurrency.
Compute the maximum possible speedup if an unlimited number of processing elements is available.
Compute the values of speedup, efficiency, and the overhead function if the number of processing elements is (i) the same as the degree of concurrency and (ii) equal to half of the degree of concurrency.
5.4 Consider a parallel system containing p processing elements solving a problem consisting of W units of work. Prove that if the isoefficiency function of the system is worse (greater) than Θ(p), then the problem cannot be solved cost-optimally with p = (W). Also prove the converse that if the problem can be solved cost-optimally only for p < Θ(W), then the isoefficiency function of the parallel system is worse than linear.
5.5 (Scaled speedup) Scaled speedup is defined as the speedup obtained when the problem size is increased linearly with the number of processing elements; that is, if W is chosen as a base problem size for a single processing element, then
For the problem of adding n numbers on p processing elements (Example 5.1), plot the speedup curves, assuming that the base problem for p = 1 is that of adding 256 numbers. Use p = 1, 4, 16, 64, and 256. Assume that it takes 10 time units to communicate a number between two processing elements, and that it takes one unit of time to add two numbers. Now plot the standard speedup curve for the base problem size and compare it with the scaled speedup curve.
Hint: The parallel runtime is (n/p − 1) + 11 log p.
5.6 Plot a third speedup curve for Problem 5.5, in which the problem size is scaled up according to the isoefficiency function, which is Θ(p log p). Use the same expression for TP .
Hint: The scaled speedup under this method of scaling is given by the following equation:
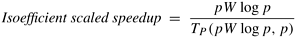
5.7 Plot the efficiency curves for the problem of adding n numbers on p processing elements corresponding to the standard speedup curve (Problem 5.5), the scaled speedup curve (Problem 5.5), and the speedup curve when the problem size is increased according to the isoefficiency function (Problem 5.6).
5.8 A drawback of increasing the number of processing elements without increasing the total workload is that the speedup does not increase linearly with the number of processing elements, and the efficiency drops monotonically. Based on your experience with Problems 5.5 and 5.7, discuss whether or not scaled speedup increases linearly with the number of processing elements in general. What can you say about the isoefficiency function of a parallel system whose scaled speedup curve matches the speedup curve determined by increasing the problem size according to the isoefficiency function?
5.9 (Time-constrained scaling) Using the expression for TP from Problem 5.5 for p = 1, 4, 16, 64, 256, 1024, and 4096, what is the largest problem that can be solved if the total execution time is not to exceed 512 time units? In general, is it possible to solve an arbitrarily large problem in a fixed amount of time, provided that an unlimited number of processing elements is available? Why?
5.10 (Prefix sums) Consider the problem of computing the prefix sums (Example 5.1) of n numbers on n processing elements. What is the parallel runtime, speedup, and efficiency of this algorithm? Assume that adding two numbers takes one unit of time and that communicating one number between two processing elements takes 10 units of time. Is the algorithm cost-optimal?
5.11 Design a cost-optimal version of the prefix sums algorithm (Problem 5.10) for computing all prefix-sums of n numbers on p processing elements where p < n. Assuming that adding two numbers takes one unit of time and that communicating one number between two processing elements takes 10 units of time, derive expressions for TP , S, E , cost, and the isoefficiency function.
5.12 [GK93a] Prove that if To ≤ (p) for a given problem size, then the parallel execution time will continue to decrease as p is increased and will asymptotically approach a constant value. Also prove that if To > Θ(p), then TP first decreases and then increases with p; hence, it has a distinct minimum.
5.13 The parallel runtime of a parallel implementation of the FFT algorithm with p processing elements is given by TP = (n/p) log n + tw(n/p) log p for an input sequence of length n (Equation 13.4 with ts = 0). The maximum number of processing elements that the algorithm can use for an n-point FFT is n. What are the values of p0 (the value of p that satisfies Equation 5.21) and
 for tw = 10?
for tw = 10?5.14 [GK93a] Consider two parallel systems with the same overhead function, but with different degrees of concurrency. Let the overhead function of both parallel systems be W 1/3 p3/2 + 0.1W 2/3 p. Plot the TP versus p curve for W = 106, and 1 ≤ p ≤ 2048. If the degree of concurrency is W1/3 for the first algorithm and W2/3 for the second algorithm, compute the values of
 for both parallel systems. Also compute the cost and efficiency for both the parallel systems at the point on the TP versus p curve where their respective minimum runtimes are achieved.
for both parallel systems. Also compute the cost and efficiency for both the parallel systems at the point on the TP versus p curve where their respective minimum runtimes are achieved.