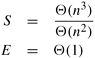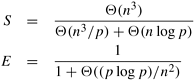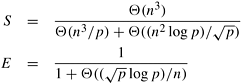Graph theory plays an important role in computer science because it provides an easy and systematic way to model many problems. Many problems can be expressed in terms of graphs, and can be solved using standard graph algorithms. This chapter presents parallel formulations of some important and fundamental graph algorithms.
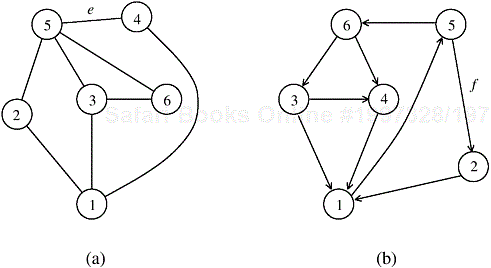
An undirected graph G is a pair (V, E), where V is a finite set of points called vertices and E is a finite set of edges. An edge e ∊ E is an unordered pair (u, v), where u, v ∊ V. An edge (u, v) indicates that vertices u and v are connected. Similarly, a directed graph G, is a pair (V, E), where V is the set of vertices as we just defined, but an edge (u, v) ∊ E is an ordered pair; that is, it indicates that there is a connection from u to v. Figure 10.1 illustrates an undirected and a directed graph. We use the term graph to refer to both directed and undirected graphs.
Many definitions are common to directed and undirected graphs, although certain terms have slightly different meanings for each. If (u, v) is an edge in an undirected graph, (u, v) is incident on vertices u and v. However, if a graph is directed, then edge (u, v) is incident from vertex u and is incident to vertex v. For example, in Figure 10.1(a), edge e is incident on vertices 5 and 4, but in Figure 10.1(b), edge f is incident from vertex 5 and incident to vertex 2. If (u, v) is an edge in a undirected graph G = (V, E), vertices u and v are said to be adjacent to each other. If the graph is directed, vertex v is said to be adjacent to vertex u.
A path from a vertex v to a vertex u is a sequence <v0, v1, v2, ..., vk> of vertices where v0 = v, vk = u, and (vi, vi+1) ∊ E for i = 0, 1, ..., k − 1. The length of a path is defined as the number of edges in the path. If there exists a path from v to u, then u is reachable from v. A path is simple if all of its vertices are distinct. A path forms a cycle if its starting and ending vertices are the same – that is, v0 = vk. A graph with no cycles is called acyclic. A cycle is simple if all the intermediate vertices are distinct. For example, in Figure 10.1(a), the sequence <3, 6, 5, 4> is a path from vertex 3 to vertex 4, and in Figure 10.1(b) there is a directed simple cycle <1, 5, 6, 4, 1>. Additionally, in Figure 10.1(a), the sequence <1, 2, 5, 3, 6, 5, 4, 1> is an undirected cycle that is not simple because it contains the loop <5, 3, 6, 5>.
An undirected graph is connected if every pair of vertices is connected by a path. We say that a graph G′ = (V′, E′) is a subgraph of G = (V, E ) if V′ ⊆ V and E′ ⊆ E. Given a set V ′ ⊆ V, the subgraph of G induced by V ′ is the graph G′ = (V ′, E ′), where E′ = {(u, v) ∊ E|u, v ∊ V′}. A complete graph is a graph in which each pair of vertices is adjacent. A forest is an acyclic graph, and a tree is a connected acyclic graph. Note that if G = (V, E) is a tree, then |E| = |V| − 1.
Sometimes weights are associated with each edge in E. Weights are usually real numbers representing the cost or benefit of traversing the associated edge. For example, in an electronic circuit a resistor can be represented by an edge whose weight is its resistance. A graph that has weights associated with each edge is called a weighted graph and is denoted by G = (V, E, w), where V and E are as we just defined and w : E → ℜ is a real-valued function defined on E. The weight of a graph is defined as the sum of the weights of its edges. The weight of a path is the sum of the weights of its edges.
There are two standard methods for representing a graph in a computer program. The first method is to use a matrix, and the second method is to use a linked list.
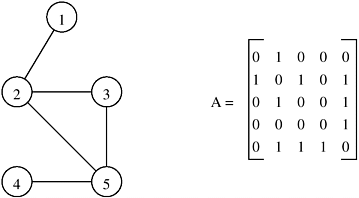
Consider a graph G = (V, E) with n vertices numbered 1, 2, ..., n. The adjacency matrix of this graph is an n × n array A = (ai, j), which is defined as follows:
Figure 10.2 illustrates an adjacency matrix representation of an undirected graph. Note that the adjacency matrix of an undirected graph is symmetric. The adjacency matrix representation can be modified to facilitate weighted graphs. In this case, A = (ai,j) is defined as follows:
We refer to this modified adjacency matrix as the weighted adjacency matrix. The space required to store the adjacency matrix of a graph with n vertices is Θ(n2).
The adjacency list representation of a graph G = (V, E ) consists of an array Adj[1..|V|] of lists. For each v ∊ V, Adj [v] is a linked list of all vertices u such that G contains an edge (v, u) ∊ E. In other words, Adj [v] is a list of all vertices adjacent to v. Figure 10.3 shows an example of the adjacency list representation. The adjacency list representation can be modified to accommodate weighted graphs by storing the weight of each edge (v, u) ∊ E in the adjacency list of vertex v. The space required to store the adjacency list is Θ(|E|).
The nature of the graph determines which representation should be used. A graph G = (V, E ) is sparse if |E| is much smaller than O (|V|2); otherwise it is dense. The adjacency matrix representation is useful for dense graphs, and the adjacency list representation is often more efficient for sparse graphs. Note that the sequential run time of an algorithm using an adjacency matrix and needing to traverse all the edges of the graph is bounded below by Ω(|V|2) because the entire array must be accessed. However, if the adjacency list representation is used, the run time is bounded below by Ω(|V| + |E|) for the same reason. Thus, if the graph is sparse (|E| is much smaller than |V|2), the adjacency list representation is better than the adjacency matrix representation.
The rest of this chapter presents several graph algorithms. The first four sections present algorithms for dense graphs, and the last section discusses algorithms for sparse graphs. We assume that dense graphs are represented by an adjacency matrix, and sparse graphs by an adjacency list. Throughout this chapter, n denotes the number of vertices in the graph.
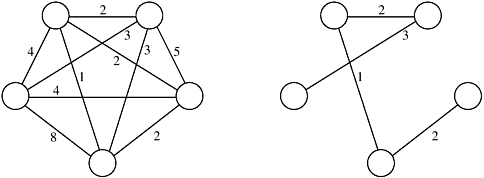
A spanning tree of an undirected graph G is a subgraph of G that is a tree containing all the vertices of G. In a weighted graph, the weight of a subgraph is the sum of the weights of the edges in the subgraph. A minimum spanning tree (MST) for a weighted undirected graph is a spanning tree with minimum weight. Many problems require finding an MST of an undirected graph. For example, the minimum length of cable necessary to connect a set of computers in a network can be determined by finding the MST of the undirected graph containing all the possible connections. Figure 10.4 shows an MST of an undirected graph.
If G is not connected, it cannot have a spanning tree. Instead, it has a spanning forest. For simplicity in describing the MST algorithm, we assume that G is connected. If G is not connected, we can find its connected components (Section 10.6) and apply the MST algorithm on each of them. Alternatively, we can modify the MST algorithm to output a minimum spanning forest.
Prim’s algorithm for finding an MST is a greedy algorithm. The algorithm begins by selecting an arbitrary starting vertex. It then grows the minimum spanning tree by choosing a new vertex and edge that are guaranteed to be in a spanning tree of minimum cost. The algorithm continues until all the vertices have been selected.
Let G = (V, E, w) be the weighted undirected graph for which the minimum spanning tree is to be found, and let A = (ai, j) be its weighted adjacency matrix. Prim’s algorithm is shown in Algorithm 10.1. The algorithm uses the set VT to hold the vertices of the minimum spanning tree during its construction. It also uses an array d[1..n] in which, for each vertex v ∊ (V − VT ), d [v] holds the weight of the edge with the least weight from any vertex in VT to vertex v. Initially, VT contains an arbitrary vertex r that becomes the root of the MST. Furthermore, d[r] = 0, and for all v such that v ∊ (V − VT ), d[v] = w(r, v) if such an edge exists; otherwise d[v] = ∞. During each iteration of the algorithm, a new vertex u is added to VT such that d[u] = min{d [v]|v ∊ (V − VT )}. After this vertex is added, all values of d[v] such that v ∊ (V − VT) are updated because there may now be an edge with a smaller weight between vertex v and the newly added vertex u. The algorithm terminates when VT = V. Figure 10.5 illustrates the algorithm. Upon termination of Prim’s algorithm, the cost of the minimum spanning tree is 
. Algorithm 10.1 can be easily modified to store the edges that belong in the minimum spanning tree.
![Prim’s minimum spanning tree algorithm. The MST is rooted at vertex b. For each iteration, vertices in VT as well as the edges selected so far are shown in bold. The array d[v] shows the values of the vertices in V − VT after they have been updated.](http://imgdetail.ebookreading.net/software_development/21/0201648652/0201648652__introduction-to-parallel__0201648652__graphics__10fig08.gif)
Figure 10.5. Prim’s minimum spanning tree algorithm. The MST is rooted at vertex b. For each iteration, vertices in VT as well as the edges selected so far are shown in bold. The array d[v] shows the values of the vertices in V − VT after they have been updated.
In Algorithm 10.1, the body of the while loop (lines 10–13) is executed n−1 times. Both the computation of min{d[v]|v ∊ (V − VT )} (line 10), and the for loop (lines 12 and 13) execute in O (n) steps. Thus, the overall complexity of Prim’s algorithm is Θ(n2).
Example 10.1. Prim’s sequential minimum spanning tree algorithm.
1. procedure PRIM_MST(V, E, w, r) 2. begin 3. VT := {r}; 4. d[r] := 0; 5. for all v ∊ (V − VT ) do 6. if edge (r, v) exists set d[v] := w(r, v); 7. else set d[v] := ∞; 8. while VT ≠ V do 9. begin 10. find a vertex u such that d[u] :=min{d[v]|v ∊ (V − VT )}; 11. VT := VT ∪ {u}; 12. for all v ∊ (V − VT ) do 13. d[v] := min{d[v], w(u, v)}; 14. endwhile 15. end PRIM_MST
Prim’s algorithm is iterative. Each iteration adds a new vertex to the minimum spanning tree. Since the value of d[v] for a vertex v may change every time a new vertex u is added in VT , it is hard to select more than one vertex to include in the minimum spanning tree. For example, in the graph of Figure 10.5, after selecting vertex b, if both vertices d and c are selected, the MST will not be found. That is because, after selecting vertex d, the value of d[c] is updated from 5 to 2. Thus, it is not easy to perform different iterations of the while loop in parallel. However, each iteration can be performed in parallel as follows.
Let p be the number of processes, and let n be the number of vertices in the graph. The set V is partitioned into p subsets using the 1-D block mapping (Section 3.4.1). Each subset has n/p consecutive vertices, and the work associated with each subset is assigned to a different process. Let Vi be the subset of vertices assigned to process Pi for i = 0, 1, ..., p − 1. Each process Pi stores the part of the array d that corresponds to Vi (that is, process Pi stores d [v] such that v ∊ Vi). Figure 10.6(a) illustrates the partitioning. Each process Pi computes di[u] = min{di[v]|v ∊ (V − VT) ∩ Vi} during each iteration of the while loop. The global minimum is then obtained over all di[u] by using the all-to-one reduction operation (Section 4.1) and is stored in process P0. Process P0 now holds the new vertex u, which will be inserted into VT. Process P0 broadcasts u to all processes by using one-to-all broadcast (Section 4.1). The process Pi responsible for vertex u marks u as belonging to set VT. Finally, each process updates the values of d[v] for its local vertices.
When a new vertex u is inserted into VT, the values of d[v] for v ∊ (V − VT) must be updated. The process responsible for v must know the weight of the edge (u, v). Hence, each process Pi needs to store the columns of the weighted adjacency matrix corresponding to set Vi of vertices assigned to it. This corresponds to 1-D block mapping of the matrix (Section 3.4.1). The space to store the required part of the adjacency matrix at each process is Θ(n2/p). Figure 10.6(b) illustrates the partitioning of the weighted adjacency matrix.
The computation performed by a process to minimize and update the values of d[v] during each iteration is Θ(n/p). The communication performed in each iteration is due to the all-to-one reduction and the one-to-all broadcast. For a p-process message-passing parallel computer, a one-to-all broadcast of one word takes time (ts + tw) log p (Section 4.1). Finding the global minimum of one word at each process takes the same amount of time (Section 4.1). Thus, the total communication cost of each iteration is Θ(log p). The parallel run time of this formulation is given by
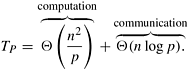
Since the sequential run time is W = Θ(n2), the speedup and efficiency are as follows:
From Equation 10.1 we see that for a cost-optimal parallel formulation (p log p)/n = O (1). Thus, this formulation of Prim’s algorithm can use only p = O (n/log n) processes. Furthermore, from Equation 10.1, the isoefficiency function due to communication is Θ(p2 log2 p). Since n must grow at least as fast as p in this formulation, the isoefficiency function due to concurrency is Θ(p2). Thus, the overall isoefficiency of this formulation is Θ(p2 log2 p).
For a weighted graph G = (V, E, w), the single-source shortest paths problem is to find the shortest paths from a vertex v ∊ V to all other vertices in V. A shortest path from u to v is a minimum-weight path. Depending on the application, edge weights may represent time, cost, penalty, loss, or any other quantity that accumulates additively along a path and is to be minimized. In the following section, we present Dijkstra’s algorithm, which solves the single-source shortest-paths problem on both directed and undirected graphs with non-negative weights.
Dijkstra’s algorithm, which finds the shortest paths from a single vertex s, is similar to Prim’s minimum spanning tree algorithm. Like Prim’s algorithm, it incrementally finds the shortest paths from s to the other vertices of G. It is also greedy; that is, it always chooses an edge to a vertex that appears closest. Algorithm 10.2 shows Dijkstra’s algorithm. Comparing this algorithm with Prim’s minimum spanning tree algorithm, we see that the two are almost identical. The main difference is that, for each vertex u ∊ (V − VT ), Dijkstra’s algorithm stores l[u], the minimum cost to reach vertex u from vertex s by means of vertices in VT; Prim’s algorithm stores d [u], the cost of the minimum-cost edge connecting a vertex in VT to u. The run time of Dijkstra’s algorithm is Θ(n2).
Example 10.2. Dijkstra’s sequential single-source shortest paths algorithm.
1. procedure DIJKSTRA_SINGLE_SOURCE_SP(V, E, w, s) 2. begin 3. VT := {s}; 4. for all v ∊ (V − VT ) do 5. if (s, v) exists set l[v] := w(s, v); 6. else set l[v] := ∞; 7. while VT ≠ V do 8. begin 9. find a vertex u such that l[u] := min{l[v]|v ∊ (V − VT )}; 10. VT := VT ∪ {u}; 11. for all v ∊ (V − VT ) do 12. l[v] := min{l[v], l[u] + w(u, v)}; 13. endwhile 14. end DIJKSTRA_SINGLE_SOURCE_SP
The parallel formulation of Dijkstra’s single-source shortest path algorithm is very similar to the parallel formulation of Prim’s algorithm for minimum spanning trees (Section 10.2). The weighted adjacency matrix is partitioned using the 1-D block mapping (Section 3.4.1). Each of the p processes is assigned n/p consecutive columns of the weighted adjacency matrix, and computes n/p values of the array l. During each iteration, all processes perform computation and communication similar to that performed by the parallel formulation of Prim’s algorithm. Consequently, the parallel performance and scalability of Dijkstra’s single-source shortest path algorithm is identical to that of Prim’s minimum spanning tree algorithm.
Instead of finding the shortest paths from a single vertex v to every other vertex, we are sometimes interested in finding the shortest paths between all pairs of vertices. Formally, given a weighted graph G(V, E, w), the all-pairs shortest paths problem is to find the shortest paths between all pairs of vertices vi, vj ∊ V such that i ≠ j. For a graph with n vertices, the output of an all-pairs shortest paths algorithm is an n × n matrix D = (di,j) such that di,j is the cost of the shortest path from vertex vi to vertex vj.
The following sections present two algorithms to solve the all-pairs shortest paths problem. The first algorithm uses Dijkstra’s single-source shortest paths algorithm, and the second uses Floyd’s algorithm. Dijkstra’s algorithm requires non-negative edge weights (Problem 10.4), whereas Floyd’s algorithm works with graphs having negative-weight edges provided they contain no negative-weight cycles.
In Section 10.3 we presented Dijkstra’s algorithm for finding the shortest paths from a vertex v to all the other vertices in a graph. This algorithm can also be used to solve the all-pairs shortest paths problem by executing the single-source algorithm on each process, for each vertex v. We refer to this algorithm as Dijkstra’s all-pairs shortest paths algorithm. Since the complexity of Dijkstra’s single-source algorithm is Θ(n2), the complexity of the all-pairs algorithm is Θ(n3).
Dijkstra’s all-pairs shortest paths problem can be parallelized in two distinct ways. One approach partitions the vertices among different processes and has each process compute the single-source shortest paths for all vertices assigned to it. We refer to this approach as the source-partitioned formulation. Another approach assigns each vertex to a set of processes and uses the parallel formulation of the single-source algorithm (Section 10.3) to solve the problem on each set of processes. We refer to this approach as the source-parallel formulation. The following sections discuss and analyze these two approaches.
Source-Partitioned Formulation. The source-partitioned parallel formulation of Dijkstra’s algorithm uses n processes. Each process Pi finds the shortest paths from vertex vi to all other vertices by executing Dijkstra’s sequential single-source shortest paths algorithm. It requires no interprocess communication (provided that the adjacency matrix is replicated at all processes). Thus, the parallel run time of this formulation is given by
Since the sequential run time is W = Θ(n3), the speedup and efficiency are as follows:
It might seem that, due to the absence of communication, this is an excellent parallel formulation. However, that is not entirely true. The algorithm can use at most n processes. Therefore, the isoefficiency function due to concurrency is Θ(p3), which is the overall isoefficiency function of the algorithm. If the number of processes available for solving the problem is small (that is, n = Θ(p)), then this algorithm has good performance. However, if the number of processes is greater than n, other algorithms will eventually outperform this algorithm because of its poor scalability.
Source-Parallel Formulation. The major problem with the source-partitioned parallel formulation is that it can keep only n processes busy doing useful work. Performance can be improved if the parallel formulation of Dijkstra’s single-source algorithm (Section 10.3) is used to solve the problem for each vertex v. The source-parallel formulation is similar to the source-partitioned formulation, except that the single-source algorithm runs on disjoint subsets of processes.
Specifically, p processes are divided into n partitions, each with p/n processes (this formulation is of interest only if p > n). Each of the n single-source shortest paths problems is solved by one of the n partitions. In other words, we first parallelize the all-pairs shortest paths problem by assigning each vertex to a separate set of processes, and then parallelize the single-source algorithm by using the set of p/n processes to solve it. The total number of processes that can be used efficiently by this formulation is O (n2).
The analysis presented in Section 10.3 can be used to derive the performance of this formulation of Dijkstra’s all-pairs algorithm. Assume that we have a p-process message-passing computer such that p is a multiple of n. The p processes are partitioned into n groups of size p/n each. If the single-source algorithm is executed on each p/n process group, the parallel run time is
Notice the similarities between Equations 10.3 and 10.2. These similarities are not surprising because each set of p/n processes forms a different group and carries out the computation independently. Thus, the time required by each set of p/n processes to solve the single-source problem determines the overall run time. Since the sequential run time is W = Θ(n3), the speedup and efficiency are as follows:
From Equation 10.4 we see that for a cost-optimal formulation p log p/n2 = O (1). Hence, this formulation can use up to O (n2/log n) processes efficiently. Equation 10.4 also shows that the isoefficiency function due to communication is Θ((p log p)1.5). The isoefficiency function due to concurrency is Θ(p1.5). Thus, the overall isoefficiency function is Θ((p log p)1.5).
Comparing the two parallel formulations of Dijkstra’s all-pairs algorithm, we see that the source-partitioned formulation performs no communication, can use no more than n processes, and solves the problem in time Θ(n2). In contrast, the source-parallel formulation uses up to n2/log n processes, has some communication overhead, and solves the problem in time Θ(n log n) when n2/log n processes are used. Thus, the source-parallel formulation exploits more parallelism than does the source-partitioned formulation.
Floyd’s algorithm for solving the all-pairs shortest paths problem is based on the following observation. Let G = (V, E, w) be the weighted graph, and let V = {v1,v2,..., vn} be the vertices of G. Consider a subset {v1, v2,..., vk} of vertices for some k where k ≤ n. For any pair of vertices vi , vj ∊ V, consider all paths from vi to vj whose intermediate vertices belong to the set {v1, v2,..., vk }. Let 
be the minimum-weight path among them, and let 
be the weight of . If vertex vk is not in the shortest path from vi to v j, then is the same as 
. However, if vk is in , then we can break into two paths – one from vi to vk and one from vk to vj. Each of these paths uses vertices from {v1, v2,..., vk−1}. Thus, 
. These observations are expressed in the following recurrence equation:
The length of the shortest path from vi to vj is given by 
. In general, the solution is a matrix 
.
Floyd’s algorithm solves Equation 10.5 bottom-up in the order of increasing values of k. Algorithm 10.3 shows Floyd’s all-pairs algorithm. The run time of Floyd’s algorithm is determined by the triple-nested for loops in lines 4–7. Each execution of line 7 takes time Θ(1); thus, the complexity of the algorithm is Θ(n3). Algorithm 10.3 seems to imply that we must store n matrices of size n ×n. However, when computing matrix D(k), only matrix D(k−1) is needed. Consequently, at most two n × n matrices must be stored. Therefore, the overall space complexity is Θ(n2). Furthermore, the algorithm works correctly even when only one copy of D is used (Problem 10.6).
Example 10.3. Floyd’s all-pairs shortest paths algorithm. This program computes the all-pairs shortest paths of the graph G = (V, E ) with adjacency matrix A.
1. procedure FLOYD_ALL_PAIRS_SP( A) 2. begin 3. D(0) = A; 4. for k := 1 to n do 5. for i := 1 to n do 6. for j := 1 to n do 7.; 8. end FLOYD_ALL_PAIRS_SP
A generic parallel formulation of Floyd’s algorithm assigns the task of computing matrix D(k) for each value of k to a set of processes. Let p be the number of processes available. Matrix D(k) is partitioned into p parts, and each part is assigned to a process. Each process computes the D(k) values of its partition. To accomplish this, a process must access the corresponding segments of the kth row and column of matrix D(k−1). The following section describes one technique for partitioning matrix D(k). Another technique is considered in Problem 10.8.
2-D Block Mapping. One way to partition matrix D(k) is to use the 2-D block mapping (Section 3.4.1). Specifically, matrix D(k) is divided into p blocks of size 
, and each block is assigned to one of the p processes. It is helpful to think of the p processes as arranged in a logical grid of size 
. Note that this is only a conceptual layout and does not necessarily reflect the actual interconnection network. We refer to the process on the ith row and jth column as Pi,j. Process Pi,j is assigned a subblock of D(k) whose upper-left corner is 
and whose lower-right corner is 
. Each process updates its part of the matrix during each iteration. Figure 10.7(a) illustrates the 2-D block mapping technique.
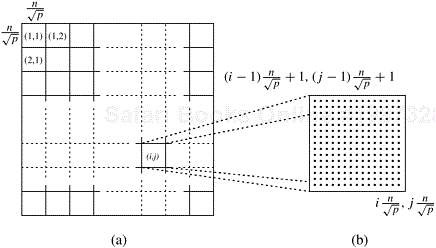
Figure 10.7. (a) Matrix D(k) distributed by 2-D block mapping into subblocks, and (b) the subblock of D(k) assigned to process Pi,j.
During the kth iteration of the algorithm, each process Pi,j needs certain segments of the kth row and kth column of the D(k−1) matrix. For example, to compute 
it must get 
and 
. As Figure 10.8 illustrates, resides on a process along the same row, and element resides on a process along the same column as Pi,j. Segments are transferred as follows. During the kth iteration of the algorithm, each of the 
processes containing part of the kth row sends it to the 
processes in the same column. Similarly, each of the processes containing part of the kth column sends it to the processes in the same row.
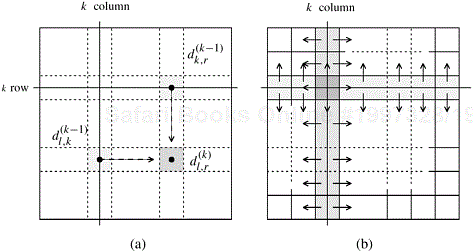
Figure 10.8. (a) Communication patterns used in the 2-D block mapping. When computing , information must be sent to the highlighted process from two other processes along the same row and column. (b) The row and column of processes that contain the kth row and column send them along process columns and rows.
Algorithm 10.4 shows the parallel formulation of Floyd’s algorithm using the 2-D block mapping. We analyze the performance of this algorithm on a p-process message-passing computer with a cross-bisection bandwidth of Θ(p). During each iteration of the algorithm, the kth row and kth column of processes perform a one-to-all broadcast along a row or a column of processes. Each such process has 
elements of the kth row or column, so it sends elements. This broadcast requires time Θ
. The synchronization step on line 7 requires time Θ(log p). Since each process is assigned n2/p elements of the D(k) matrix, the time to compute corresponding D(k) values is Θ(n2/p). Therefore, the parallel run time of the 2-D block mapping formulation of Floyd’s algorithm is
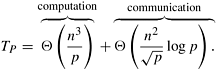
Since the sequential run time is W = Θ(n3), the speedup and efficiency are as follows:
From Equation 10.6 we see that for a cost-optimal formulation 
; thus, 2-D block mapping can efficiently use up to O(n2/log2n) processes. Equation 10.6 can also be used to derive the isoefficiency function due to communication, which is Θ(p1.5 log3 p). The isoefficiency function due to concurrency is Θ(p1.5). Thus, the overall isoefficiency function is Θ(p1.5 log3 p).
Speeding Things Up. In the 2-D block mapping formulation of Floyd’s algorithm, a synchronization step ensures that all processes have the appropriate segments of matrix D(k−1) before computing elements of matrix D(k) (line 7 in Algorithm 10.4). In other words, the kth iteration starts only when the (k − 1)th iteration has completed and the relevant parts of matrix D(k−1) have been transmitted to all processes. The synchronization step can be removed without affecting the correctness of the algorithm. To accomplish this, a process starts working on the kth iteration as soon as it has computed the (k −1)th iteration and has the relevant parts of the D(k−1) matrix. This formulation is called pipelined 2-D block mapping. A similar technique is used in Section 8.3 to improve the performance of Gaussian elimination.
Example 10.4. Floyd’s parallel formulation using the 2-D block mapping. P∗,j denotes all the processes in the jth column, and Pi,∗ denotes all the processes in the ith row. The matrix D(0) is the adjacency matrix.
1. procedure FLOYD_2DBLOCK(D(0)) 2. begin 3. for k := 1 to n do 4. begin 5. each process Pi,j that has a segment of the kth row of D(k−1); broadcasts it to the P∗,j processes; 6. each process Pi,j that has a segment of the kth column of D(k−1); broadcasts it to the Pi,∗ processes; 7. each process waits to receive the needed segments; 8. each process Pi,j computes its part of the D(k) matrix; 9. end 10. end FLOYD_2DBLOCK
Consider a p-process system arranged in a two-dimensional topology. Assume that process Pi,j starts working on the kth iteration as soon as it has finished the (k − 1)th iteration and has received the relevant parts of the D(k−1) matrix. When process Pi,j has elements of the kth row and has finished the (k − 1)th iteration, it sends the part of matrix D(k−1) stored locally to processes Pi,j −1 and Pi, j +1. It does this because that part of the D(k−1) matrix is used to compute the D(k) matrix. Similarly, when process Pi,j has elements of the kth column and has finished the (k − 1)th iteration, it sends the part of matrix D(k−1) stored locally to processes Pi −1, j and Pi +1, j. When process Pi,j receives elements of matrix D(k) from a process along its row in the logical mesh, it stores them locally and forwards them to the process on the side opposite from where it received them. The columns follow a similar communication protocol. Elements of matrix D(k) are not forwarded when they reach a mesh boundary. Figure 10.9 illustrates this communication and termination protocol for processes within a row (or a column).
Figure 10.9. Communication protocol followed in the pipelined 2-D block mapping formulation of Floyd’s algorithm. Assume that process 4 at time t has just computed a segment of the kth column of the D(k−1) matrix. It sends the segment to processes 3 and 5. These processes receive the segment at time t + 1 (where the time unit is the time it takes for a matrix segment to travel over the communication link between adjacent processes). Similarly, processes farther away from process 4 receive the segment later. Process 1 (at the boundary) does not forward the segment after receiving it.
Consider the movement of values in the first iteration. In each step, elements of the first row are sent from process Pi,j to Pi +1,j. Similarly, elements of the first column are sent from process Pi,j to process Pi,j+1. Each such step takes time Θ(). After Θ
steps, process 
gets the relevant elements of the first row and first column in time Θ(n). The values of successive rows and columns follow after time Θ(n2/p) in a pipelined mode. Hence, process finishes its share of the shortest path computation in time Θ(n3/p) + Θ(n). When process has finished the (n − 1)th iteration, it sends the relevant values of the nth row and column to the other processes. These values reach process P1,1 in time Θ(n). The overall parallel run time of this formulation is
Since the sequential run time is W = Θ(n3), the speedup and efficiency are as follows:
Table 10.1. The performance and scalability of the all-pairs shortest paths algorithms on various architectures with O (p) bisection bandwidth. Similar run times apply to all k − d cube architectures, provided that processes are properly mapped to the underlying processors.
|
Maximum Number of Processes for E = Θ(1) |
Corresponding Parallel Run Time |
Isoefficiency Function | |
|---|---|---|---|
|
Dijkstra source-partitioned |
Θ(n) |
Θ(n2) |
Θ(p3) |
|
Dijkstra source-parallel |
Θ(n2/log n) |
Θ(n log n) |
Θ((p log p)1.5) |
|
Floyd 1-D block |
Θ(n/log n) |
Θ(n2 log n) |
Θ((p log p)3) |
|
Floyd 2-D block |
Θ(n2/log2 n) |
Θ(n log2 n) |
Θ(p1.5 log3 p) |
|
Floyd pipelined 2-D block |
Θ(n2) |
Θ(n) |
Θ(p1.5) |
From Equation 10.7 we see that for a cost-optimal formulation p/n2 = O (1). Thus, the pipelined formulation of Floyd’s algorithm uses up to O (n2) processes efficiently. Also from Equation 10.7, we can derive the isoefficiency function due to communication, which is Θ(p1.5). This is the overall isoefficiency function as well. Comparing the pipelined formulation to the synchronized 2-D block mapping formulation, we see that the former is significantly faster.
The performance of the all-pairs shortest paths algorithms previously presented is summarized in Table 10.1 for a parallel architecture with O (p) bisection bandwidth. Floyd’s pipelined formulation is the most scalable and can use up to Θ(n2) processes to solve the problem in time Θ(n). Moreover, this parallel formulation performs equally well even on architectures with bisection bandwidth O , such as a mesh-connected computer. Furthermore, its performance is independent of the type of routing (store-and-forward or cut-through).
In many applications we wish to determine if any two vertices in a graph are connected. This is usually done by finding the transitive closure of a graph. Formally, if G = (V, E) is a graph, then the transitive closure of G is defined as the graph G∗ = (V, E∗), where E∗ = {(vi, vj)| there is a path from vi to vj in G}. We compute the transitive closure of a graph by computing the connectivity matrix A∗. The connectivity matrix of G is a matrix 
such that 
if there is a path from vi to vj or i = j, and 
otherwise.
To compute A∗ we assign a weight of 1 to each edge of E and use any of the all-pairs shortest paths algorithms on this weighted graph. Matrix A∗ can be obtained from matrix D, where D is the solution to the all-pairs shortest paths problem, as follows:
Another method for computing A∗ is to use Floyd’s algorithm on the adjacency matrix of G, replacing the min and + operations in line 7 of Algorithm 10.3 by logical or and logical and operations. In this case, we initially set ai,j = 1 if i = j or (vi, vj) ∊ E, and ai,j = 0 otherwise. Matrix A∗ is obtained by setting if di,j = 0 and otherwise. The complexity of computing the transitive closure is Θ(n3).
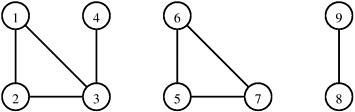
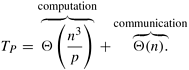
The connected components of an undirected graph G = (V, E) are the maximal disjoint sets C1, C2, ..., Ck such that V = C1 ∪ C2 ∪ ... ∪ Ck , and u, v ∊ Ci if and only if u is reachable from v and v is reachable from u. The connected components of an undirected graph are the equivalence classes of vertices under the “is reachable from” relation. For example, Figure 10.10 shows a graph with three connected components.
We can find the connected components of a graph by performing a depth-first traversal on the graph. The outcome of this depth-first traversal is a forest of depth-first trees. Each tree in the forest contains vertices that belong to a different connected component. Figure 10.11 illustrates this algorithm. The correctness of this algorithm follows directly from the definition of a spanning tree (that is, a depth-first tree is also a spanning tree of a graph induced by the set of vertices in the depth-first tree) and from the fact that G is undirected. Assuming that the graph is stored using a sparse representation, the run time of this algorithm is Θ(|E|) because the depth-first traversal algorithm traverses all the edges in G.
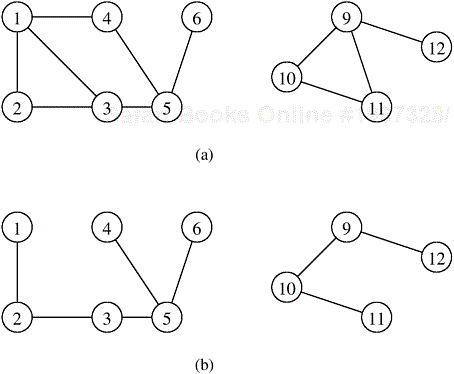
Figure 10.11. Part (b) is a depth-first forest obtained from depth-first traversal of the graph in part (a). Each of these trees is a connected component of the graph in part (a).
The connected-component algorithm can be parallelized by partitioning the adjacency matrix of G into p parts and assigning each part to one of p processes. Each process Pi has a subgraph Gi of G, where Gi = (V, Ei) and Ei are the edges that correspond to the portion of the adjacency matrix assigned to this process. In the first step of this parallel formulation, each process Pi computes the depth-first spanning forest of the graph Gi. At the end of this step, p spanning forests have been constructed. During the second step, spanning forests are merged pairwise until only one spanning forest remains. The remaining spanning forest has the property that two vertices are in the same connected component of G if they are in the same tree. Figure 10.12 illustrates this algorithm.
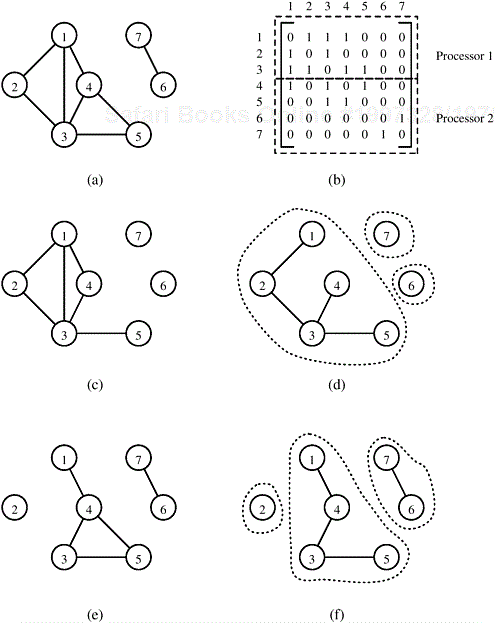
Figure 10.12. Computing connected components in parallel. The adjacency matrix of the graph G in (a) is partitioned into two parts as shown in (b). Next, each process gets a subgraph of G as shown in (c) and (e). Each process then computes the spanning forest of the subgraph, as shown in (d) and (f). Finally, the two spanning trees are merged to form the solution.
To merge pairs of spanning forests efficiently, the algorithm uses disjoint sets of edges. Assume that each tree in the spanning forest of a subgraph of G is represented by a set. The sets for different trees are pairwise disjoint. The following operations are defined on the disjoint sets:
find(x) returns a pointer to the representative element of the set containing x. Each set has its own unique representative.
union(x, y) unites the sets containing the elements x and y. The two sets are assumed to be disjoint prior to the operation.
The spanning forests are merged as follows. Let A and B be the two spanning forests to be merged. At most n − 1 edges (since A and B are forests) of one are merged with the edges of the other. Suppose we want to merge forest A into forest B. For each edge (u, v) of A, a find operation is performed for each vertex to determine if the two vertices are already in the same tree of B . If not, then the two trees (sets) of B containing u and v are united by a union operation. Otherwise, no union operation is necessary. Hence, merging A and B requires at most 2(n − 1) find operations and (n − 1) union operations. We can implement the disjoint-set data structure by using disjoint-set forests with ranking and path compression. Using this implementation, the cost of performing 2(n − 1) finds and (n − 1) unions is O (n). A detailed description of the disjoint-set forest is beyond the scope of this book. Refer to the bibliographic remarks (Section 10.8) for references.
Having discussed how to efficiently merge two spanning forests, we now concentrate on how to partition the adjacency matrix of G and distribute it among p processes. The next section discusses a formulation that uses 1-D block mapping. An alternative partitioning scheme is discussed in Problem 10.12.
1-D Block Mapping. The n × n adjacency matrix is partitioned into p stripes (Section 3.4.1). Each stripe is composed of n/p consecutive rows and is assigned to one of the p processes. To compute the connected components, each process first computes a spanning forest for the n-vertex graph represented by the n/p rows of the adjacency matrix assigned to it.
Consider a p-process message-passing computer. Computing the spanning forest based on the (n/p) × n adjacency matrix assigned to each process requires time Θ(n2/p). The second step of the algorithm–the pairwise merging of spanning forests – is performed by embedding a virtual tree on the processes. There are log p merging stages, and each takes time Θ(n). Thus, the cost due to merging is Θ(n log p). Finally, during each merging stage, spanning forests are sent between nearest neighbors. Recall that Θ(n) edges of the spanning forest are transmitted. Thus, the communication cost is Θ(n log p). The parallel run time of the connected-component algorithm is
Since the sequential complexity is W = Θ(n2), the speedup and efficiency are as follows:
From Equation 10.8 we see that for a cost-optimal formulation p = O (n/log n). Also from Equation 10.8, we derive the isoefficiency function, which is Θ(p2 log2 p). This is the isoefficiency function due to communication and due to the extra computations performed in the merging stage. The isoefficiency function due to concurrency is Θ(p2); thus, the overall isoefficiency function is Θ(p2 log2 p). The performance of this parallel formulation is similar to that of Prim’s minimum spanning tree algorithm and Dijkstra’s single-source shortest paths algorithm on a message-passing computer.
The parallel algorithms in the previous sections are based on the best-known algorithms for dense-graph problems. However, we have yet to address parallel algorithms for sparse graphs. Recall that a graph G = (V, E) is sparse if |E| is much smaller than |V|2. Figure 10.13 shows some examples of sparse graphs.
Figure 10.13. Examples of sparse graphs: (a) a linear graph, in which each vertex has two incident edges; (b) a grid graph, in which each vertex has four incident vertices; and (c) a random sparse graph.
Any dense-graph algorithm works correctly on sparse graphs as well. However, if the sparseness of the graph is taken into account, it is usually possible to obtain significantly better performance. For example, the run time of Prim’s minimum spanning tree algorithm (Section 10.2) is Θ(n2) regardless of the number of edges in the graph. By modifying Prim’s algorithm to use adjacency lists and a binary heap, the complexity of the algorithm reduces to Θ(|E| log n). This modified algorithm outperforms the original algorithm as long as |E|=O (n2/log n). An important step in developing sparse-graph algorithms is to use an adjacency list instead of an adjacency matrix. This change in representation is crucial, since the complexity of adjacency-matrix-based algorithms is usually Ω(n2), and is independent of the number of edges. Conversely, the complexity of adjacency-list-based algorithms is usually Ω(n + |E|), which depends on the sparseness of the graph.
In the parallel formulations of sequential algorithms for dense graphs, we obtained good performance by partitioning the adjacency matrix of a graph so that each process performed roughly an equal amount of work and communication was localized. We were able to achieve this largely because the graph was dense. For example, consider Floyd’s all-pairs shortest paths algorithm. By assigning equal-sized blocks from the adjacency matrix to all processes, the work was uniformly distributed. Moreover, since each block consisted of consecutive rows and columns, the communication overhead was limited.
However, it is difficult to achieve even work distribution and low communication overhead for sparse graphs. Consider the problem of partitioning the adjacency list of a graph. One possible partition assigns an equal number of vertices and their adjacency lists to each process. However, the number of edges incident on a given vertex may vary. Hence, some processes may be assigned a large number of edges while others receive very few, leading to a significant work imbalance among the processes. Alternately, we can assign an equal number of edges to each process. This may require splitting the adjacency list of a vertex among processes. As a result, the time spent communicating information among processes that store separate parts of the adjacency list may increase dramatically. Thus, it is hard to derive efficient parallel formulations for general sparse graphs (Problems 10.14 and 10.15). However, we can often derive efficient parallel formulations if the sparse graph has a certain structure. For example, consider the street map shown in Figure 10.14. The graph corresponding to the map is sparse: the number of edges incident on any vertex is at most four. We refer to such graphs as grid graphs. Other types of sparse graphs for which an efficient parallel formulation can be developed are those corresponding to well-shaped finite element meshes, and graphs whose vertices have similar degrees. The next two sections present efficient algorithms for finding a maximal independent set of vertices, and for computing single-source shortest paths for these types of graphs.
Figure 10.14. A street map (a) can be represented by a graph (b). In the graph shown in (b), each street intersection is a vertex and each edge is a street segment. The vertices of (b) are the intersections of (a) marked by dots.
Consider the problem of finding a maximal independent set (MIS) of vertices of a graph. We are given a sparse undirected graph G = (V, E). A set of vertices I ⊂ V is called independent if no pair of vertices in I is connected via an edge in G. An independent set is called maximal if by including any other vertex not in I, the independence property is violated. These definitions are illustrated in Figure 10.15. Note that as the example illustrates, maximal independent sets are not unique. Maximal independent sets of vertices can be used to determine which computations can be done in parallel in certain types of task graphs. For example, maximal independent sets can be used to determine the sets of rows that can be factored concurrently in parallel incomplete factorization algorithms, and to compute a coloring of a graph in parallel.
Many algorithms have been proposed for computing a maximal independent set of vertices. The simplest class of algorithms starts by initially setting I to be empty, and assigning all vertices to a set C that acts as the candidate set of vertices for inclusion in I . Then the algorithm proceeds by repeatedly moving a vertex v from C into I and removing all vertices adjacent to v from C. This process terminates when C becomes empty, in which case I is a maximal independent set. The resulting set I will contain an independent set of vertices, because every time we add a vertex into I we remove from C all the vertices whose subsequent inclusion will violate the independence condition. Also, the resulting set is maximal, because any other vertex that is not already in I is adjacent to at least one of the vertices in I.
Even though the above algorithm is very simple, it is not well suited for parallel processing, as it is serial in nature. For this reason parallel MIS algorithms are usually based on the randomized algorithm originally developed by Luby for computing a coloring of a graph. Using Luby’s algorithm, a maximal independent set I of vertices V a graph is computed in an incremental fashion as follows. The set I is initially set to be empty, and the set of candidate vertices, C, is set to be equal to V. A unique random number is assigned to each vertex in C, and if a vertex has a random number that is smaller than all of the random numbers of the adjacent vertices, it is included in I. The set C is updated so that all the vertices that were selected for inclusion in I and their adjacent vertices are removed from it. Note that the vertices that are selected for inclusion in I are indeed independent (i.e., not directly connected via an edge). This is because, if v was inserted in I, then the random number assigned to v is the smallest among the random numbers assigned to its adjacent vertices; thus, no other vertex u adjacent to v will have been selected for inclusion. Now the above steps of random number assignment and vertex selection are repeated for the vertices left in C, and I is augmented similarly. This incremental augmentation of I ends when C becomes empty. On the average, this algorithm converges after O (log |V|) such augmentation steps. The execution of the algorithm for a small graph is illustrated in Figure 10.16. In the rest of this section we describe a shared-address-space parallel formulation of Luby’s algorithm. A message-passing adaption of this algorithm is described in the message-passing chapter.
Figure 10.16. The different augmentation steps of Luby’s randomized maximal independent set algorithm. The numbers inside each vertex correspond to the random number assigned to the vertex.
A parallel formulation of Luby’s MIS algorithm for a shared-address-space parallel computer is as follows. Let I be an array of size |V|. At the termination of the algorithm, I [i] will store one, if vertex vi is part of the MIS, or zero otherwise. Initially, all the elements in I are set to zero, and during each iteration of Luby’s algorithm, some of the entries of that array will be changed to one. Let C be an array of size |V|. During the course of the algorithm, C [i] is one if vertex vi is part of the candidate set, or zero otherwise. Initially, all the elements in C are set to one. Finally, let R be an array of size |V| that stores the random numbers assigned to each vertex.
During each iteration, the set C is logically partitioned among the p processes. Each process generates a random number for its assigned vertices from C. When all the processes finish generating these random numbers, they proceed to determine which vertices can be included in I. In particular, for each vertex assigned to them, they check to see if the random number assigned to it is smaller than the random numbers assigned to all of its adjacent vertices. If it is true, they set the corresponding entry in I to one. Because R is shared and can be accessed by all the processes, determining whether or not a particular vertex can be included in I is quite straightforward.
Array C can also be updated in a straightforward fashion as follows. Each process, as soon as it determines that a particular vertex v will be part of I, will set to zero the entries of C corresponding to its adjacent vertices. Note that even though more than one process may be setting to zero the same entry of C (because it may be adjacent to more than one vertex that was inserted in I), such concurrent writes will not affect the correctness of the results, because the value that gets concurrently written is the same.
The complexity of each iteration of Luby’s algorithm is similar to that of the serial algorithm, with the extra cost of the global synchronization after each random number assignment. The detailed analysis of Luby’s algorithm is left as an exercise (Problem 10.16).
It is easy to modify Dijkstra’s single-source shortest paths algorithm so that it finds the shortest paths for sparse graphs efficiently. The modified algorithm is known as Johnson’s algorithm. Recall that Dijkstra’s algorithm performs the following two steps in each iteration. First, it extracts a vertex u ∊ (V − VT) such that l[u] = min{l[v]|v ∊ (V − VT)} and inserts it into set VT. Second, for each vertex v ∊ (V − VT), it computes l[v] = min{l[v], l[u] + w(u, v)}. Note that, during the second step, only the vertices in the adjacency list of vertex u need to be considered. Since the graph is sparse, the number of vertices adjacent to vertex u is considerably smaller than Θ(n); thus, using the adjacency-list representation improves performance.
Johnson’s algorithm uses a priority queue Q to store the value l[v] for each vertex v ∊ (V − VT). The priority queue is constructed so that the vertex with the smallest value in l is always at the front of the queue. A common way to implement a priority queue is as a binary min-heap. A binary min-heap allows us to update the value l[v] for each vertex v in time O (log n). Algorithm 10.5 shows Johnson’s algorithm. Initially, for each vertex v other than the source, it inserts l[v] = ∞ in the priority queue. For the source vertex s it inserts l[s] = 0. At each step of the algorithm, the vertex u ∊ (V − VT) with the minimum value in l is removed from the priority queue. The adjacency list for u is traversed, and for each edge (u, v) the distance l[v] to vertex v is updated in the heap. Updating vertices in the heap dominates the overall run time of the algorithm. The total number of updates is equal to the number of edges; thus, the overall complexity of Johnson’s algorithm is Θ(|E| log n).
Example 10.5. Johnson’s sequential single-source shortest paths algorithm.
1. procedure JOHNSON_SINGLE_SOURCE_SP(V, E, s) 2. begin 3. Q := V ; 4. for all v ∊ Q do 5. l[v] := ∞; 6. l[s] := 0; 7. while Q ≠ 0 do 8. begin 9. u := extract min( Q); 10. for each v ∊ Adj [u] do 11. if v ∊ Q and l[u] + w(u, v) < l[v] then 12. l[v] := l[u] + w(u, v); 13. endwhile 14. end JOHNSON_SINGLE_SOURCE_SP
An efficient parallel formulation of Johnson’s algorithm must maintain the priority queue Q efficiently. A simple strategy is for a single process, for example, P0, to maintain Q. All other processes will then compute new values of l[v] for v ∊ (V − VT), and give them to P0 to update the priority queue. There are two main limitation of this scheme. First, because a single process is responsible for maintaining the priority queue, the overall parallel run time is O (|E| log n) (there are O (|E|) queue updates and each update takes time O (log n)). This leads to a parallel formulation with no asymptotic speedup, since O (|E| log n) is the same as the sequential run time. Second, during each iteration, the algorithm updates roughly |E|/|V| vertices. As a result, no more than |E|/|V| processes can be kept busy at any given time, which is very small for most of the interesting classes of sparse graphs, and to a large extent, independent of the size of the graphs.
The first limitation can be alleviated by distributing the maintainance of the priority queue to multiple processes. This is a non-trivial task, and can only be done effectively on architectures with low latency, such as shared-address-space computers. However, even in the best case, when each priority queue update takes only time O (1), the maximum speedup that can be achieved is O (log n), which is quite small. The second limitation can be alleviated by recognizing the fact that depending on the l value of the vertices at the top of the priority queue, more than one vertex can be extracted at the same time. In particular, if v is the vertex at the top of the priority queue, all vertices u such that l[u] = l[v] can also be extracted, and their adjacency lists processed concurrently. This is because the vertices that are at the same minimum distance from the source can be processed in any order. Note that in order for this approach to work, all the vertices that are at the same minimum distance must be processed in lock-step. An additional degree of concurrency can be extracted if we know that the minimum weight over all the edges in the graph is m. In that case, all vertices u such that l[u] ≤ l[v] + m can be processed concurrently (and in lock-step). We will refer to these as the safe vertices. However, this additional concurrency can lead to asymptotically better speedup than O (log n) only if more than one update operation of the priority queue can proceed concurrently, substantially complicating the parallel algorithm for maintaining the single priority queue.
Our discussion thus far was focused on developing a parallel formulation of Johnson’s algorithm that finds the shortest paths to the vertices in the same order as the serial algorithm, and explores concurrently only safe vertices. However, as we have seen, such an approach leads to complicated algorithms and limited concurrency. An alternate approach is to develop a parallel algorithm that processes both safe and unsafe vertices concurrently, as long as these unsafe vertices can be reached from the source via a path involving vertices whose shortest paths have already been computed (i.e., their corresponding l-value in the priority queue is not infinite). In particular, in this algorithm, each one of the p processes extracts one of the p top vertices and proceeds to update the l values of the vertices adjacent to it. Of course, the problem with this approach is that it does not ensure that the l values of the vertices extracted from the priority queue correspond to the cost of the shortest path. For example, consider two vertices v and u that are at the top of the priority queue, with l[v] < l[u]. According to Johnson’s algorithm, at the point a vertex is extracted from the priority queue, its l value is the cost of the shortest path from the source to that vertex. Now, if there is an edge connecting v and u, such that l[v] + w(v, u) < l[u], then the correct value of the shortest path to u is l[v] + w(v, u), and not l[u]. However, the correctness of the results can be ensured by detecting when we have incorrectly computed the shortest path to a particular vertex, and inserting it back into the priority queue with the updated l value. We can detect such instances as follows. Consider a vertex v that has just been extracted from the queue, and let u be a vertex adjacent to v that has already been extracted from the queue. If l[v] + w(v, u) is smaller than l[u], then the shortest path to u has been incorrectly computed, and u needs to be inserted back into the priority queue with l[u] = l[v] + w(v, u).
To see how this approach works, consider the example grid graph shown in Figure 10.17. In this example, there are three processes and we want to find the shortest path from vertex a. After initialization of the priority queue, vertices b and d will be reachable from the source. In the first step, process P0 and P1 extract vertices b and d and proceed to update the l values of the vertices adjacent to b and d. In the second step, processes P0, P1, and P2 extract e, c, and g, and proceed to update the l values of the vertices adjacent to them. Note that when processing vertex e, process P0 checks to see if l[e] + w(e, d) is smaller or greater than l[d]. In this particular example, l[e] + w(e, d) > l[d], indicating that the previously computed value of the shortest path to d does not change when e is considered, and all computations so far are correct. In the third step, processes P0 and P1 work on h and f, respectively. Now, when process P0 compares l[h] + w(h, g) = 5 against the value of l[g] = 10 that was extracted in the previous iteration, it finds it to be smaller. As a result, it inserts back into the priority queue vertex g with the updated l[g] value. Finally, in the fourth and last step, the remaining two vertices are extracted from the priority queue, and all single-source shortest paths have been computed.
Figure 10.17. An example of the modified Johnson’s algorithm for processing unsafe vertices concurrently.
This approach for parallelizing Johnson’s algorithm falls into the category of speculative decomposition discussed in Section 3.2.4. Essentially, the algorithm assumes that the l[] values of the top p vertices in the priority queue will not change as a result of processing some of these vertices, and proceeds to perform the computations required by Johnson’s algorithm. However, if at some later point it detects that its assumptions were wrong, it goes back and essentially recomputes the shortest paths of the affected vertices.
In order for such a speculative decomposition approach to be effective, we must also remove the bottleneck of working with a single priority queue. In the rest of this section we present a message-passing algorithm that uses speculative decomposition to extract concurrency and in which there is no single priority queue. Instead, each process maintains its own priority queue for the vertices that it is assigned to. Problem 10.13 discusses another approach.
Let p be the number of processes, and let G = (V, E) be a sparse graph. We partition the set of vertices V into p disjoint sets V1, V2, ..., Vp, and assign each set of vertices and its associated adjacency lists to one of the p processes. Each process maintains a priority queue for the vertices assigned to it, and computes the shortest paths from the source to these vertices. Thus, the priority queue Q is partitioned into p disjoint priority queues Q1, Q2, ..., Qp, each assigned to a separate process. In addition to the priority queue, each process Pi also maintains an array sp such that sp[v] stores the cost of the shortest path from the source vertex to v for each vertex v ∊ Vi. The cost sp[v] is updated to l[v] each time vertex v is extracted from the priority queue. Initially, sp[v] = ∞ for every vertex v other than the source, and we insert l[s] into the appropriate priority queue for the source vertex s. Each process executes Johnson’s algorithm on its local priority queue. At the end of the algorithm, sp[v] stores the length of the shortest path from source to vertex v.
When process Pi extracts the vertex u ∊ Vi with the smallest value l[u] from Qi, the l values of vertices assigned to processes other than Pi may need to be updated. Process Pi sends a message to processes that store vertices adjacent to u, notifying them of the new values. Upon receiving these values, processes update the values of l. For example, assume that there is an edge (u, v) such that u ∊ Vi and v ∊ Vj, and that process Pi has just extracted vertex u from its priority queue. Process Pi then sends a message to Pj containing the potential new value of l[v], which is l[u] + w(u, v). Process Pj, upon receiving this message, sets the value of l[v] stored in its priority queue to min{l[v], l[u] + w(u, v)}.
Since both processes Pi and Pj execute Johnson’s algorithm, it is possible that process Pj has already extracted vertex v from its priority queue. This means that process Pj might have already computed the shortest path sp[v] from the source to vertex v. Then there are two possible cases: either sp[v] ≤ l[u] + w(u, v), or sp[v] > l[u] + w(u, v). The first case means that there is a longer path to vertex v passing through vertex u, and the second case means that there is a shorter path to vertex v passing through vertex u. For the first case, process Pj needs to do nothing, since the shortest path to v does not change. For the second case, process Pj must update the cost of the shortest path to vertex v. This is done by inserting the vertex v back into the priority queue with l[v] = l[u] + w(u, v) and disregarding the value of sp[v]. Since a vertex v can be reinserted into the priority queue, the algorithm terminates only when all the queues become empty.
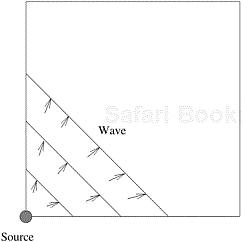
Initially, only the priority queue of the process with the source vertex is non-empty. After that, the priority queues of other processes become populated as messages containing new l values are created and sent to adjacent processes. When processes receive new l values, they insert them into their priority queues and perform computations. Consider the problem of computing the single-source shortest paths in a grid graph where the source is located at the bottom-left corner. The computations propagate across the grid graph in the form of a wave. A process is idle before the wave arrives, and becomes idle again after the wave has passed. This process is illustrated in Figure 10.18. At any time during the execution of the algorithm, only the processes along the wave are busy. The other processes have either finished their computations or have not yet started them. The next sections discuss three mappings of grid graphs onto a p-process mesh.
2-D Block Mapping. One way to map an n × n grid graph onto p processors is to use the 2-D block mapping (Section 3.4.1). Specifically, we can view the p processes as a logical mesh and assign a different block of 
vertices to each process. Figure 10.19 illustrates this mapping.
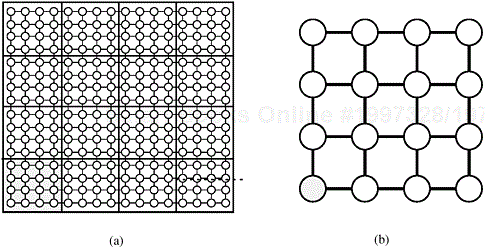
Figure 10.19. Mapping the grid graph (a) onto a mesh, and (b) by using the 2-D block mapping. In this example, n = 16 and 
. The shaded vertices are mapped onto the shaded process.
At any time, the number of busy processes is equal to the number of processes intersected by the wave. Since the wave moves diagonally, no more than O () processes are busy at any time. Let W be the overall work performed by the sequential algorithm. If we assume that, at any time, processes are performing computations, and if we ignore the overhead due to inter-process communication and extra work, then the maximum speedup and efficiency are as follows:
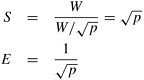
The efficiency of this mapping is poor and becomes worse as the number of processes increases.
2-D Cyclic Mapping. The main limitation of the 2-D block mapping is that each process is responsible for only a small, confined area of the grid. Alternatively, we can make each process responsible for scattered areas of the grid by using the 2-D cyclic mapping (Section 3.4.1). This increases the time during which a process stays busy. In 2-D cyclic mapping, the n × n grid graph is divided into n2/p blocks, each of size . Each block is mapped onto the process mesh. Figure 10.20 illustrates this mapping. Each process contains a block of n2/p vertices. These vertices belong to diagonals of the graph that are vertices apart. Each process is assigned roughly 
such diagonals.
Figure 10.20. Mapping the grid graph (a) onto a mesh, and (b) by using the 2-D cyclic mapping. In this example, n = 16 and = 4. The shaded graph vertices are mapped onto the correspondingly shaded mesh processes.
Now each process is responsible for vertices that belong to different parts of the grid graph. As the wave propagates through the graph, the wave intersects some of the vertices on each process. Thus, processes remain busy for most of the algorithm. The 2-D cyclic mapping, though, incurs a higher communication overhead than does the 2-D block mapping. Since adjacent vertices reside on separate processes, every time a process extracts a vertex u from its priority queue it must notify other processes of the new value of l[u]. The analysis of this mapping is left as an exercise (Problem 10.17).
1-D Block Mapping. The two mappings discussed so far have limitations. The 2-D block mapping fails to keep more than O () processes busy at any time, and the 2-D cyclic mapping has high communication overhead. Another mapping treats the p processes as a linear array and assigns n/p stripes of the grid graph to each processor by using the 1-D block mapping. Figure 10.21 illustrates this mapping.
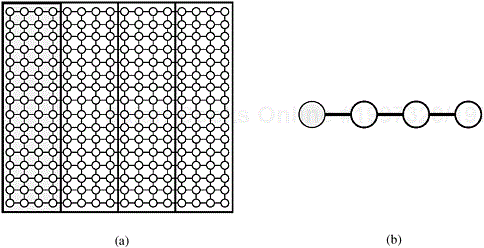
Figure 10.21. Mapping the grid graph (a) onto a linear array of processes (b). In this example, n = 16 and p = 4. The shaded vertices are mapped onto the shaded process.
Initially, the wave intersects only one process. As computation progresses, the wave spills over to the second process so that two processes are busy. As the algorithm continues, the wave intersects more processes, which become busy. This process continues until all p processes are busy (that is, until they all have been intersected by the wave). After this point, the number of busy processes decreases. Figure 10.22 illustrates the propagation of the wave. If we assume that the wave propagates at a constant rate, then p/2 processes (on the average) are busy. Ignoring any overhead, the speedup and efficiency of this mapping are as follows:
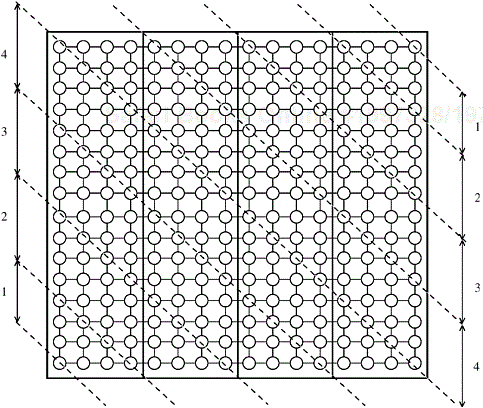
Figure 10.22. The number of busy processes as the computational wave propagates across the grid graph.
Thus, the efficiency of this mapping is at most 50 percent. The 1-D block mapping is substantially better than the 2-D block mapping but cannot use more than O (n) processes.
Detailed discussions of graph theory and graph algorithms can be found in numerous texts. Gibbons [Gib85] provides a good reference to the algorithms presented in this chapter. Aho, Hopcroft, and Ullman [AHU74], and Cormen, Leiserson, and Rivest [CLR90] provide a detailed description of various graph algorithms and issues related to their efficient implementation on sequential computers.
The sequential minimum spanning tree algorithm described in Section 10.2 is due to Prim [Pri57]. Bentley [Ben80] and Deo and Yoo [DY81] present parallel formulations of Prim’s MST algorithm. Deo and Yoo’s algorithm is suited to a shared-address-space computer. It finds the MST in Θ(n1.5) using Θ(n0.5) processes. Bentley’s algorithm works on a tree-connected systolic array and finds the MST in time Θ(n log n) using n/log n processes. The hypercube formulation of Prim’s MST algorithm in Section 10.2 is similar to Bentley’s algorithm.
The MST of a graph can be also computed by using either Kruskal’s [Kru56] or Sollin’s [Sol77] sequential algorithms. The complexity of Sollin’s algorithm (Problem 10.21) is Θ(n2 log n). Savage and Jaja [SJ81] have developed a formulation of Sollin’s algorithm for the CREW PRAM. Their algorithm uses n2 processes and solves the problem in time Θ(log2 n). Chin, Lam, and Chen [CLC82] have developed a formulation of Sollin’s algorithm for a CREW PRAM that uses 
processes and finds the MST in time Θ(log2 n). Awerbuch and Shiloach [AS87] present a formulation of Sollin’s algorithm for the shuffle-exchange network that uses Θ(n2) processes and runs in time Θ(log2 n). Doshi and Varman [DV87] present a Θ(n2/p) time algorithm for a p-process ring-connected computer for Sollin’s algorithm. Leighton [Lei83] and Nath, Maheshwari, and Bhatt [NMB83] present parallel formulations of Sollin’s algorithm for a mesh of trees network. The first algorithm runs in Θ(log2 n) and the second algorithm runs in Θ(log4 n) for an n × n mesh of trees. Huang [Hua85] describes a formulation of Sollin’s algorithm that runs in Θ(n2/p) on a mesh of trees.
The single-source shortest paths algorithm in Section 10.3 was discovered by Dijkstra [Dij59]. Due to the similarity between Dijkstra’s algorithm and Prim’s MST algorithm, all the parallel formulations of Prim’s algorithm discussed in the previous paragraph can also be applied to the single-source shortest paths problem. Bellman [Bel58] and Ford [FR62] independently developed a single-source shortest paths algorithm that operates on graphs with negative weights but without negative-weight cycles. The Bellman-Ford single-source algorithm has a sequential complexity of O (|V||E|). Paige and Kruskal [PK89] present parallel formulations of both the Dijkstra and Bellman-Ford single-source shortest paths algorithm. Their formulation of Dijkstra’s algorithm runs on an EREW PRAM of Θ(n) processes and runs in time Θ(n log n). Their formulation of Bellman-Ford’s algorithm runs in time Θ(n|E|/p + n log p) on a p-process EREW PRAM where p ≤ |E|. They also present algorithms for the CRCW PRAM [PK89].
Significant work has been done on the all-pairs shortest paths problem. The source-partitioning formulation of Dijkstra’s all-pairs shortest paths is discussed by Jenq and Sahni [JS87] and Kumar and Singh [KS91b]. The source parallel formulation of Dijkstra’s all-pairs shortest paths algorithm is discussed by Paige and Kruskal [PK89] and Kumar and Singh [KS91b]. The Floyd’s all-pairs shortest paths algorithm discussed in Section 10.4.2 is due to Floyd [Flo62]. The 1-D and 2-D block mappings (Problem 10.8) are presented by Jenq and Sahni [JS87], and the pipelined version of Floyd’s algorithm is presented by Bertsekas and Tsitsiklis [BT89] and Kumar and Singh [KS91b]. Kumar and Singh [KS91b] present isoefficiency analysis and performance comparison of different parallel formulations for the all-pairs shortest paths on hypercube- and mesh-connected computers. The discussion in Section 10.4.3 is based upon the work of Kumar and Singh [KS91b] and of Jenq and Sahni [JS87]. In particular, Algorithm 10.4 is adopted from the paper by Jenq and Sahni [JS87]. Levitt and Kautz [LK72] present a formulation of Floyd’s algorithm for two-dimensional cellular arrays that uses n2 processes and runs in time Θ(n). Deo, Pank, and Lord have developed a parallel formulation of Floyd’s algorithm for the CREW PRAM model that has complexity Θ(n) on n2 processes. Chandy and Misra [CM82] present a distributed all-pairs shortest-path algorithm based on diffusing computation.
The connected-components algorithm discussed in Section 10.6 was discovered by Woo and Sahni [WS89]. Cormen, Leiserson, and Rivest [CLR90] discusses ways to efficiently implement disjoint-set data structures with ranking and path compression. Several algorithms exist for computing the connected components; many of them are based on the technique of vertex collapsing, similar to Sollin’s algorithm for the minimum spanning tree. Most of the parallel formulations of Sollin’s algorithm can also find the connected components. Hirschberg [Hir76] and Hirschberg, Chandra, and Sarwate [HCS79] developed formulations of the connected-components algorithm based on vertex collapsing. The former has a complexity of Θ(log2 n) on a CREW PRAM with n2 processes, and the latter has similar complexity and uses 
processes. Chin, Lam, and Chen [CLC81] made the vertex collapse algorithm more efficient by reducing the number of processes to 
for a CREW PRAM, while keeping the run time at Θ(log2 n). Nassimi and Sahni [NS80] used the vertex collapsing technique to develop a formulation for a mesh-connected computer that finds the connected components in time Θ(n) by using n2 processes.
The single-source shortest paths algorithm for sparse graphs, discussed in Section 10.7.2, was discovered by Johnson [Joh77]. Paige and Kruskal [PK89] discuss the possibility of maintaining the queue Q in parallel. Rao and Kumar [RK88a] presented techniques to perform concurrent insertions and deletions in a priority queue. The 2-D block mapping, 2-D block-cyclic mapping, and 1-D block mapping formulation of Johnson’s algorithm (Section 10.7.2) are due to Wada and Ichiyoshi [WI89]. They also presented theoretical and experimental evaluation of these schemes on a mesh-connected parallel computer.
The serial maximal independent set algorithm described in Section 10.7.1 was developed by Luby [Lub86] and its parallel formulation on shared-address-space architectures was motivated by the algorithm described by Karypis and Kumar [KK99]. Jones and Plassman [JP93] have developed an asynchronous variation of Luby’s algorithm that is particularly suited for distributed memory parallel computers. In their algorithm, each vertex is assigned a single random number, and after a communication step, each vertex determines the number of its adjacent vertices that have smaller and greater random numbers. At this point each vertex gets into a loop waiting to receive the color values of its adjacent vertices that have smaller random numbers. Once all these colors have been received, the vertex selects a consistent color, and sends it to all of its adjacent vertices with greater random numbers. The algorithm terminates when all vertices have been colored. Note that besides the initial communication step to determine the number of smaller and greater adjacent vertices, this algorithm proceeds asynchronously.
Other parallel graph algorithms have been proposed. Shiloach and Vishkin [SV82] presented an algorithm for finding the maximum flow in a directed flow network with n vertices that runs in time O (n2 log n) on an n-process EREW PRAM. Goldberg and Tarjan [GT88] presented a different maximum-flow algorithm that runs in time O (n2 log n) on an n-process EREW PRAM but requires less space. Atallah and Kosaraju [AK84] proposed a number of algorithms for a mesh-connected parallel computer. The algorithms they considered are for finding the bridges and articulation points of an undirected graph, finding the length of the shortest cycle, finding an MST, finding the cyclic index, and testing if a graph is bipartite. Tarjan and Vishkin [TV85] presented algorithms for computing the biconnected components of a graph. Their CRCW PRAM formulation runs in time Θ(log n) by using Θ(|E| + |V|) processes, and their CREW PRAM formulation runs in time Θ(log2 n) by using Θ(n2/log2 n) processes.
10.1 In the parallel formulation of Prim’s minimum spanning tree algorithm (Section 10.2), the maximum number of processes that can be used efficiently on a hypercube is Θ(n/log n). By using Θ(n/log n) processes the run time is Θ(n log n). What is the run time if you use Θ(n) processes? What is the minimum parallel run time that can be obtained on a message-passing parallel computer? How does this time compare with the run time obtained when you use Θ(n/log n) processes?
10.2 Show how Dijkstra’s single-source algorithm and its parallel formulation (Section 10.3) need to be modified in order to output the shortest paths instead of the cost. Analyze the run time of your sequential and parallel formulations.
10.3 Given a graph G = (V, E), the breadth-first ranking of vertices of G are the values assigned to the vertices of V in a breadth-first traversal of G from a node v. Show how the breadth-first ranking of vertices of G can be performed on a p-process mesh.
10.4 Dijkstra’s single-source shortest paths algorithm (Section 10.3) requires non-negative edge weights. Show how Dijkstra’s algorithm can be modified to work on graphs with negative weights but no negative cycles in time Θ(|E||V|). Analyze the performance of the parallel formulation of the modified algorithm on a p-process message-passing architecture.
10.5 Compute the total amount of memory required by the different parallel formulations of the all-pairs shortest paths problem described in Section 10.4.
10.6 Show that Floyd’s algorithm in Section 10.4.2 is correct if we replace line 7 of Algorithm 10.3 by the following line:
10.7 Compute the parallel run time, speedup, and efficiency of Floyd’s all-pairs shortest paths algorithm using 2-D block mapping on a p-process mesh with store-and-forward routing and a p-process hypercube and a p-process mesh with cut-through routing.
10.8 An alternative way of partitioning the matrix D(k) in Floyd’s all-pairs shortest paths algorithm is to use the 1-D block mapping (Section 3.4.1). Each of the p processes is assigned n/p consecutive columns of the D(k) matrix.
Compute the parallel run time, speedup, and efficiency of 1-D block mapping on a hypercube-connected parallel computer. What are the advantages and disadvantages of this partitioning over the 2-D block mapping presented in Section 10.4.2?
Compute the parallel run time, speedup, and efficiency of 1-D block mapping on a p-process mesh with store-and-forward routing, a p-process mesh with cut-through routing, and a p-process ring.
10.9 Describe and analyze the performance of a parallel formulation of Floyd’s algorithm that uses 1-D block mapping and the pipelining technique described in Section 10.4.2.
10.10 Compute the exact parallel run time, speedup, and efficiency of Floyd’s pipelined formulation (Section 10.4.2).
10.11 Compute the parallel run time, the speedup, and the efficiency of the parallel formulation of the connected-component algorithm presented in Section 10.6 for a p-process mesh with store-and-forward routing and with cut-through routing. Comment on the difference in the performance of the two architectures.
10.12 The parallel formulation for the connected-component problem presented in Section 10.6 uses 1-D block mapping to partition the matrix among processes. Consider an alternative parallel formulation in which 2-D block mapping is used instead. Describe this formulation and analyze its performance and scalability on a hypercube, a mesh with SF-routing, and a mesh with CT-routing. How does this scheme compare with 1-D block mapping?
10.13 Consider the problem of parallelizing Johnson’s single-source shortest paths algorithm for sparse graphs (Section 10.7.2). One way of parallelizing it is to use p1 processes to maintain the priority queue and p2 processes to perform the computations of the new l values. How many processes can be efficiently used to maintain the priority queue (in other words, what is the maximum value for p1)? How many processes can be used to update the l values? Is the parallel formulation that is obtained by using the p1 + p2 processes cost-optimal? Describe an algorithm that uses p1 processes to maintain the priority queue.
10.14 Consider Dijkstra’s single-source shortest paths algorithm for sparse graphs (Section 10.7). We can parallelize this algorithm on a p-process hypercube by splitting the n adjacency lists among the processes horizontally; that is, each process gets n/p lists. What is the parallel run time of this formulation? Alternatively, we can partition the adjacency list vertically among the processes; that is, each process gets a fraction of each adjacency list. If an adjacency list contains m elements, then each process contains a sublist of m/p elements. The last element in each sublist has a pointer to the element in the next process. What is the parallel run time and speedup of this formulation? What is the maximum number of processes that it can use?
10.15 Repeat Problem 10.14 for Floyd’s all-pairs shortest paths algorithm.
10.16 Analyze the performance of Luby’s shared-address-space algorithm for finding a maximal independent set of vertices on sparse graphs described in Section 10.7.1. What is the parallel run time and speedup of this formulation?
10.17 Compute the parallel run time, speedup, and efficiency of the 2-D cyclic mapping of the sparse graph single-source shortest paths algorithm (Section 10.7.2) for a mesh-connected computer. You may ignore the overhead due to extra work, but you should take into account the overhead due to communication.
10.18 Analyze the performance of the single-source shortest paths algorithm for sparse graphs (Section 10.7.2) when the 2-D block-cyclic mapping is used (Section 3.4.1). Compare it with the performance of the 2-D cyclic mapping computed in Problem 10.17. As in Problem 10.17, ignore extra computation but include communication overhead.
10.19 Consider the 1-D block-cyclic mapping described in Section 3.4.1. Describe how you will apply this mapping to the single-source shortest paths problem for sparse graphs. Compute the parallel run time, speedup, and efficiency of this mapping. In your analysis, include the communication overhead but not the overhead due to extra work.
10.20 Of the mapping schemes presented in Section 10.7.2 and in Problems 10.18 and 10.19, which one has the smallest overhead due to extra computation?
10.21 Sollin’s algorithm (Section 10.8) starts with a forest of n isolated vertices. In each iteration, the algorithm simultaneously determines, for each tree in the forest, the smallest edge joining any vertex in that tree to a vertex in another tree. All such edges are added to the forest. Furthermore, two trees are never joined by more than one edge. This process continues until there is only one tree in the forest – the minimum spanning tree. Since the number of trees is reduced by a factor of at least two in each iteration, this algorithm requires at most log n iterations to find the MST. Each iteration requires at most O (n2) comparisons to find the smallest edge incident on each vertex; thus, its sequential complexity is Θ(n2 log n). Develop a parallel formulation of Sollin’s algorithm on an n-process hypercube-connected parallel computer. What is the run time of your formulation? Is it cost optimal?