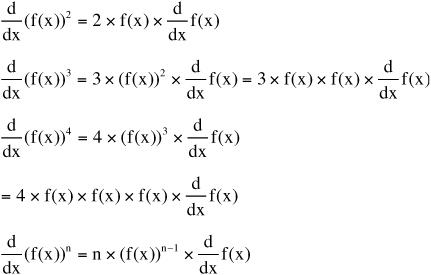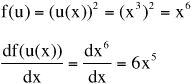6.1 Definition
6.2 Evaluating Derivatives
6.3 Differentiating Multivariable Functions
6.4 Differentiating Polynomials
6.5 Derivatives and Graphs of Functions
6.6 Adding and Subtracting Derivatives of Functions
6.7 Multiple or Repeated Derivatives of a Function
6.8 Derivatives of Products and Powers of Functions
6.9 Derivatives of Quotients of Functions
6.10 The Chain Rule for Differentiating Complicated Functions
6.11 Differentiation of Implicit vs. Explicit Functions
6.12 Using Derivatives to Determine the Shape of the Graph of a Function (Minimum and Maximum Points)
6.13 Other Rules of Differentiation
6.14 An Application of Differentiation: Curvilinear Motion
• The derivative is used to describe the rate of change of something, such as velocity, as well as the concept of the tangent to a curve (see Section 6.5). There are many applications of the derivative including but not limited to tangents, slopes, rates of change, curvilinear and straight-line motion, maxima and minima, and tests for extrema.
• For example, the time rate of change of an object in motion such as a car, plane, pitcher’s fast ball, etc., is the rate of change of distance with respect to time, and is called velocity. In other words, velocity is the derivative or rate of change of distance with respect to time.
• Remember, from rate problems, distance equals rate times time, or d = rt. (d = rt was first introduced in Section 1.4, “Simple word problems,” in the second book of the Math Masters series, Algebra.) Therefore:
The time rate of change of distance is velocity.
Also, the time rate of change of velocity is acceleration.
• The derivative can be used to study the rate of change of something that changes or varies with respect to some parameter such as position or time. For example:
The number of ants in an ant farm population over a period of time.
The rate of change in the cost of producing computers with respect to the number of computers manufactured. (Producing higher volumes costs less because parts are purchased at volume discounts.)
• To develop the definition of the derivative, consider the velocity of an airplane flying from the east coast to the west coast.
The distance the airplane is from its starting point or any defined reference point is a function of time (depends on time) or f(t). (In this example, f is the distance function.)
At time = t, the airplane is f(t) units from the starting or reference point. (The units could be hours.)
At time = t + h, the airplane is f(t + h) units from the starting or reference point and h represents an increment of time.
The change in the position of the airplane during the increment of time h is f(t + h) – f(t).
The rate of change of the distance with respect to time between time = t and time = t + h is the average velocity of the airplane.
The average velocity during this time period =
To find the velocity of the airplane at a particular point when time = t, shrink the time increment h surrounding time t. The velocity at the point where time = t is called the instantaneous velocity, and is determined by taking the limit as the increment of time h shrinks to zero.
As h gets close to zero (but not equal to zero), the time increment h and the distance f(t + h) – f(t) will get smaller.
• To determine velocity at time t or v(t):
Determine f(t + h) and f(t).
Subtract f(t) from f(t + h).
Divide f(t + h) – f(t) by h.
Take the limit as h approaches zero.
• Example: Find the velocity at t = 2 hours, if the distance in miles is represented by f(t) = 3t2.
Determine f(t h) and f(t).
f(t + h) = 3(2 + h)2 = 3(2 + h)(2 + h)
= 3(4 + 2h + 2h + h2) = 3(4 + 4h + h2)
= 12 + 12h + 3h2
f(t) = 3(2)2 = 12
Subtract f(t) from f(t + h).
f(t + h) – f(t) = (12 + 12h + 3h2) – 12 = 12h + 3h2
Divide f(t + h) – f(t) by h.
Take the limit as h approaches zero.
v(2hrs) = Limh→0(12 + 3h) = 12
Therefore, the velocity at t = 2 hours is 12 miles/hour.
• The definition of the derivative with respect to time of the distance function f(t) can be written:
provided the limit exists.
• The definition of the derivative with respect to some function of x can be written:
• Symbols for the derivative of a function f include:
• Symbols for the derivative of a function of f(x) include:
• Because velocity is the derivative of the distance function, the velocity at time t describes the distance at f(t).
If x = distance and x(t) = distance with respect to time, then:
• Acceleration is the time rate of change of velocity, and acceleration depends on time.
Acceleration = a(t) = v′(t) = x″(t)
• To evaluate a derivative, a formula described in the following section is generally used rather than the definition of the derivative.
• Evaluating derivatives using the definition of the derivative is labor intensive.
Instead, there is a shortcut formula used to evaluate derivatives. This derivative formula is derived from the definition of the derivative (see Master Math: Calculus for the derivation). The derivative formula can be applied as follows:
Where x represents any variable and n is any number.
Where c represents any constant number.
The derivative of a constant number by itself is zero.
Where f(x) represents any function.
• The following are examples of using the derivative formula to evaluate derivatives:
• The derivative formula is used to differentiate multivariable functions with respect to one of the variables.
• When a function that contains more than one variable is differentiated, the derivative formula is applied to the variable that is being differentiated.
• Apply the derivative formula to the variable (x, y, or z) in each multivariable function that it is differentiated with respect to:
| Differentiated with respect to x. |
| Differentiated with respect to y. |
| Differentiated withh respect to z. |
• To differentiate a polynomial function, the derivative formula is applied to each term separately. Remember, each term is separated by a plus or minus sign.
• For example, differentiate the following polynomial function term by term using the derivative formula:
• In this section, the relationship between graphs of functions and the derivative, the slope, and the tangent is discussed.
• In the graph of a function, the slope of a line drawn tangent to the curve through point (a, f(a)) on the curve is the derivative of the function at point (a, f(a)).

The slope of the tangent at point (a, f(a)) equals the derivative f′(a). (Note that if a tangent line is vertical, its slope is undefined.)
• The definition of the derivative can be used to prove that the slope of a line drawn tangent to a graph of a function is the derivative at that point.
Imagine two points on the curve, (a, f(a)) and (a+h, f(a+h)), with a tangent line drawn through each point. Tangent 1 is drawn through point (a, f(a)) and Tangent 2 is drawn through point (a+h, f(a+h)).

If a third line is drawn through the two tangent points (center line shown in illustration), the slope of the center line is given by the change in y over the change in x, between the two points.
Therefore, the slope of the line through (a, f(a)) and (a + h, f(a + h)) is given by:
The slope of this line is approximately equal to the slope of Tangent 1. If the value of the increment h between the two points is reduced, the value of h will approach zero, and the Tangent 2 line through point (a + h, f(a + h)) will approach being equal to the Tangent 1 line through point (a, f(a)).
Also, the line drawn through both points will approach becoming equal to the Tangent 1 and Tangent 2 lines. Therefore, the following is true:
provided the limit exists.
This is the definition of the derivative and equals f′(a).
Therefore, the slope of the tangent at (a, f(a)) is the derivative of f at a.
• The equation for a line passing through some point (a, b) with a slope of m is given by:
y – b = m(x – a)
Because the tangent line passes through point (a, f(a)) and the slope is f′(a), the equation for the tangent line is written:
y – f(a) = f′(a)(x – a)
or by rearranging,
 = slope of the tangent to a curvey = f(x)
= slope of the tangent to a curvey = f(x)
• Note: If for a given point on the graph of a function, the derivative does not exist, then that point may be at the end of the curve, at a corner on the curve, or the tangent line is a vertical line and has no slope. Also, if the derivative does not exist at a point, then the graph may be discontinuous at that point. Conversely, if the derivative does exist at a point, then the graph is continuous at that point.
• To differentiate functions that are added or subtracted, differentiate each function separately, then add or subtract. Also, if one of the functions contains a polynomial, remember to differentiate the polynomial term by term.
• Differentiate the sum of the two functions f(x) and g(x).
(See Master Math: Calculus for proofs using the definition of the derivative.)
If f(x) = 2x2 and g(x) = x3 + 3, find
 .
.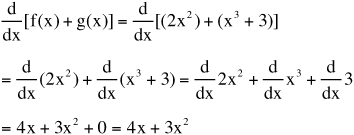
• To find the second, third, fourth, etc., derivative of a function, repeatedly apply the derivative formula for each specified derivative.
• Example: What is the second derivative of f(x) = x2?
f(x) = x2
Take first derivative.
f′(x) = 2x
Take second derivative.
f″(x) = 2
• Notation for taking multiple derivatives is:
For the nth derivative:
For the second derivative:
For the third derivative:
• In this section, differentiating products and powers of functions using the product rule, extensions of the product rule, and an alternative method are described.
• The product rule can be used to differentiate the product of two functions. The product rule applied to the product of the two functions f(x) and g(x) is:
Using shorthand notation the product rule is written:
(fg)′ = f′g + fg′
(See Master Math: Calculus for a proof of the product rule.)
• Example: If f(x) = x2 and g(x) = x3 + 3, find
![]() using the product rule.
using the product rule.
To differentiate the product ![]() using the product rule, (fg)′ = f′g = fg′:
using the product rule, (fg)′ = f′g = fg′:
First evaluate f′ and g′.
f′(x) = 2x
g′(x) = 3x2 + 0 = 3x2
Apply the product rule.
Multiply using the distributive property.
=(2x4 + 6x) + (3x4)
Combine like terms.
=(2x4 + 3x4) + 6x = 5x4 + 6x
Therefore, ![]() .
.
(Note that in this example, the monomial and binomial can be multiplied first, then differentiated term by term.)
• An extension of the product rule can be applied to derivatives of multiple products.
For two functions f and g:
(fg)′ = f′g + fg′
For three functions f, g, and h:
(fgh)′ = f′gh + fg′h + fgh′
For four functions f, g, h, and p:
(fghp)′ = f ′ ghp + fg′hp + fgh′p + fghp′
• The product rule can be applied to find the derivative of a function raised to the second power.
• For example, use the product rule to find the derivative of the binomial (x3 + x2) raised to the second power.
Apply the product rule.
Substituting: ![]()
Differentiate each binomial term by term.
= (3x2 + 2x) × (x3 + x2) + (x3 + x2) × (3x2 + 2x)
Multiply the binomials.
= (3x5 + 3x4 + 2x4 + 2x3) + (3x5 + 2x4 + 3x4 + 2x3)
Combine like terms.
= 3x5 + 3x5 + 3x4 + 2x4 + 2x4 + 3x4 + 2x3 + 2x3
= (3 + 3)x5 + (3 + 2 + 2 + 3)x4 + (2 + 2)x3
= 6x5 + 10x4 + 4x3
Therefore,
 .
.
(Note that in this example, the two binomials can be multiplied first, then differentiated term by term.)
• An alternative method can be used to evaluate the derivatives of products and powers of functions.
• To compare this method with the product rule, evaluate the derivative in the previous example of the binomial function.
f(x) =(x3 + x2)2
Find f′(x) using
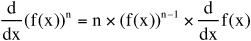 .
.
Multiply the two binomials.
= 2 × (3x5 + 2x4 + 3x4 + 2x3)
Multiply the 2 using the distributive property.
= 6x5 + 4x4 + 6x4 + 4x3
Combine like terms.
= 6x5 + 10x4 + 4x3
Therefore, ![]() .
.
This is the same result obtained above using the product rule.
• The quotient rule can be applied to evaluate derivatives of quotients of functions. For the functions f(x) and g(x) the quotient rule is:
Using notation, the quotient rule can be written:
(See Master Math: Calculus for a proof of the quotient rule.)
• For example, use the quotient rule to find the derivative of the quotient of functions f and g.
f(x) = x2 + 2 and g(x) = x3 + 3
To find the derivative of the quotient:
First evaluate f′(x) and g′(x).
f′(x) = 2x
g′(x) = 3x2
Apply the quotient rule:
The quotient becomes:
Take derivatives.
Combine like terms.

Therefore,
 .
.
• The chain rule can be used to differentiate functions in which variables depend on other variables. Consider the function f that depends on the variable u, but u depends on the variable x. In other words, f is a function of u, and u is a function of x. The chain rule is:
• For example, if f(u) = (u(x))2 and u(x) = x3, the chain rule is:
Substitute u(x) = x3.
= 2x3 × 3x2 = 6x5
Therefore,
 .
.
Because this is a simple example, u(x) = x3 can be substituted into f(u) = (u(x))2 directly, and the derivative taken.
• The chain rule can be used to break complex functions into two simpler functions. Consider the derivative:
To simplify and use the chain rule, let f(u) = (u(x))3 and u(x) = (x2 + x).
Using the chain rule, ![]() ,
,
substitute for f(u) and u(x).
Differentiate.
Substitute u(x) = (x2 + x).
Multiply the first two binomials.
= 3 × (x4 + x3 + x3 + x2) × (2x + 1)
Combine like terms.
= 3 × (x4 + 2x3 + x2) × (2x + 1)
Multiply the binomial and the trinomial.
= 3 × [(2x5 + 4x4 + 2x3) + (x4 + 2x3 + x2)]
Combine like terms, then multiply the 3.
= 3 × [2x5 + 5x4 + 4x3 + x2] = 6x5 + 15x4 + 12x3 + 3x2
Therefore,
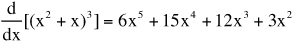 .
.
• Note that the method described in Section 6.8, “Derivatives of Products and Powers of Functions,” can also be applied to this problem, using:
• The chain rule can be applied to the parametric equations. If a point (x, y) can be described in terms of a third variable t, called the parameter, the equations are called parametric equations. If x = f(t) and y = g(t), then dx/dt and dy/dt can be determined using the chain rule.
• If y is given explicitly as a function of x, it is not difficult to obtain ![]() , because if y = f(x), then
, because if y = f(x), then ![]() .
.
This is explicit differentiation. However, if y is given implicity as a function of x, for example, f(x, y) = 2, then rather than solving the equation for y first, the equation can be differentiated as it is term by term, then solved for ![]() in terms of x and y. This called implicit differentiation.
in terms of x and y. This called implicit differentiation.
• Consider a function that is explicitly in terms of x:
f(x) = 2x2 + 4
If we let f(x) = y(x), then:
y(x) = 2x2 + 4
Rearranging.
2x2 + 4 – y(x) = 0
Therefore, y is given implicitly as a function of x.
• For example, evaluate dy/dx for the above relation, which implicitly gives y as a function of x.
2x2 + 4 – y(x) = 0
Rearrange.
y(x) = 2x2 + 4
Take the derivative of each term with respect to x.
• Example: Suppose we want to find the slope of a line tangent to the graph of a function such as:
xy(x) + x = 5
Remember, in the graph of a function, the slope of a line drawn tangent to the curve through a point on the curve is the derivative of the function at that point. To find the slope of a line tangent to the graph, the derivative of y with respect to x, or dy/dx, must be taken.
Take the derivative term by term.
Evaluate the first term using the product rule
(fg)′ = f′g = fg′.

Evaluate the second term.
Evaluate the third term.
The entire function becomes:
Rearrange to isolate dy/dx.
This equation represents the slope of the tangent line at point (x, y(x)).
• Evaluating first and second derivatives of functions to find minimum and maximum points, and local extrema of a function is a common application of the derivative. When experiments or evaluations are conducted in science, business, engineering, etc., data is gathered, relationships are developed, and graphs are constructed in order to assist in the understanding of the data and to predict future patterns and events. Information depicted in the graphs, such as where the graph is rising or falling, convex or concave, and where the high and low points are (which correspond to the maximum and minimum values), are all crucial to the evaluation of the data.
• For example, if a farmer develops and graphs a function to describe the population of bees on her farm during some period of time, she can determine whether the population of bees is increasing or decreasing during certain smaller time intervals by the sign of the derivative at those intervals.
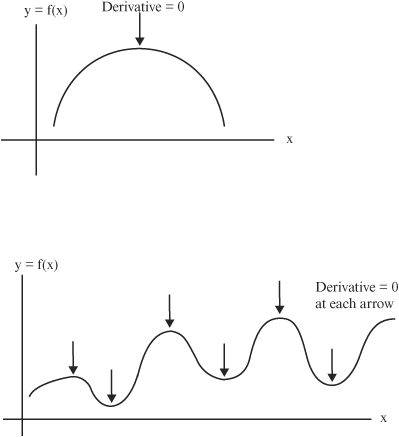
• The sign of the derivative of a function describes the shape of the graph of the function at the point where the derivative is taken. For the graph:

If f(x) is decreasing as x is increasing, the sign of the derivative is negative. Therefore, f′(x) < 0 where the graph of f is decreasing.
If f(x) is increasing as x is increasing, the sign of the derivative is positive. Therefore, f′(x) > 0 where the graph of f is increasing.
If the graph of the function is horizontal, the derivative of f is zero. Therefore, f′(x) = 0 where the graph of f is horizontal.
• A point where the graph of a function is horizontal may represent a minimum or maximum point. There are examples where a graph will not have a minimum or maximum, such as if the graph is a straight horizontal or vertical line. A minimum or maximum on the graph may be the minimum or maximum of the function, or there may be many “local” minimum or maximum points called local extrema.
• Consider the following graph of continuous function f:

If the highest point on f is the point (m, f(m)), then f(m) is the maximum value of f, and f(m) ≥ f(x) for all x. In this graph there are two extrema points, a minimum and a maximum in between points a and b.
• To find the local extrema of a function, the graph can be inspected or the derivative can be evaluated. At the extrema points, the derivative of the function f is equal to zero.
If f(n) is a minimum point and f(m) is a maximum point, and:
If f′(n) and f′(m) exist, then f′(n) = 0 and f′(m) = 0.
• As a general rule, for a given function f, all values of x where f′(x) = 0 or where f′(x) is undefined, represent all possible local extrema. Note that there may be cases where f′(x) = 0 but an extrema does not exist.
• To find all possible local extrema (minimum or maximum values of f) within some interval between x = a and x = b or between points (a, f(a)) and (b, f(b)):
Find all x values that satisfy f′(x) = 0 or f′(x) = undefined.
Evaluate each x value found in the first step by substituting it into the function f.
Evaluate values of x at the ends of the interval (at a and b) to find f(a) and f(b).
The largest value in the second step is the maximum of f(x) and the smallest value is the minimum of f(x) within the interval a – b.
• For example, find the minimum and maximum of the function f(x) = x2 + 2x between the interval of x = 0 and x = –2 where –2 ≤ x ≤ 0.
Find all x values that satisfy f′(x) = 0 or f′(x) = undefined.
Where does f′(x) = 0?
Because f′(x) = 2x = 2, set 2x + 2 = 0,
2x + 2 = 0
2x = –2
x = –2/2 = –1
Evaluate each x value found by substituting it into the function f. Evaluate f(x) at x = –1.
f(–1) = x2 + 2x = (–1)2 + 2(–1) = 1 + –2 = –1
Evaluate the values of x at the ends of the interval (at a and b) to find f(a) and f(b).
Evaluate f(x) = x2 + 2x at the end points –2 and 0.
f(–2) = (–2)2 + 2(–2) = 4 + –4 = 0
–f(0) = (0)2 + 2(0) = 0 + 0 = 0
Therefore, the number for the critical points of f over this interval (–2 ≤ x ≤ 0) are:
f(–1) = –1, f(0) = 0, and f(–2) = 0
The largest and smallest values from the second step is the maximum of f(x) and the minimum of f(x) within the interval a-b. In this example, only f(–1) = –1 was derived from the second step. The largest and smallest numbers computed overall are 0 and – 1, which represent the minimum and maximum points.
Plot the function f(x) = x2 + 2x between the interval of x = 0 and x = –2. Select x values at and near the minimum and maximum points, and solve for f(x).
Values for x are –3, –2, –1, 0, 1,
resulting in f(x) values 3, 0, –1, 0, 3.
Resulting pairs are (–3, 3), (–2, 0), (–1, –1), (0, 0), (1, 3).
Graphing the pairs is depicted as:

Therefore, because f′(–1) = 0 within the interval a-b (x = –2 and x = 0), at f(–1), the graph of the function f(x) = x2 + 2x has a minimum.
• By taking the second derivative of a function, it can be determined whether a local extrema is a minimum or a maximum.
• If point P is in the domain set of the function f and if f′(P) exists and f′(P) = 0, then using the second derivative the following is true:
If f″(P) > 0 the graph of function f is concave up at P.
If f″(P) < 0 the graph of function f is concave down at P.
In other words, if f′(P) exists, and:
If f′(P) = 0 and if f″(P) > 0 then f has a local minimum at P.
If f′(P) = 0 and if f″(P) < 0 then f has a local maximum at P.

• Remember the previous function f(x) = x2 + 2x, by taking the second derivative determine whether there is a minimum or a maximum at the point where f′(x) = 0.
At what value of x does f′(x) = 0?
2x + 2 = 0
2x = –2
x = –2/2 = –1
Therefore, at x = –1, f′(x) = 0.
Taking the second derivative:
Using the second derivative rule, because 2 is a positive number, we can predict that the graph of f(x) at x = –1 is concave up and is at a minimum. This was depicted in the graph in the previous example.
• In this section, selected derivatives of the following functions are given. See Master Math: Calculus for a more in-depth study.
Function | Derivative |
|---|---|
• y = un |
|
Where n is any positive integer and u is a function of x.
• y = au |
|
Where u is a function of x.
• y = uv |
|
Where u and v are functions of x.
• y = eu |
|
Where u is a function of x.
Where u is a function of x.
• y = logu |
|
Where u is a function of x and u ≠ 0.
• y = cosu |
|
Where u is a function of x.
• y = sinu |
|
Where u is a function of x.
• Expressions for velocity and acceleration of a particle moving along a curve (curvilinear motion) are more complicated than for a particle moving in a straight line. The equation of the curve can be given in parametric form as x = f(t) and y = g(t), where t represents time. Velocity v is a vector tangent to the curve and has an x and a y component, and is expressed in terms of magnitude (speed) and direction.
Velocity is defined for the x and y components:
The x component of velocity:
The y component of velocity:
The magnitude (speed) of v:
The direction of v:
Acceleration is given for the x and y components:
The x component of acceleration:
The y component of acceleration:
The magnitude of a:
The direction of a:
The acceleration vector can be expressed in a tangent component and a normal component to the curve.
The tangent component of acceleration:
The normal component of acceleration: