• A sequence is a set of numbers called terms, which are arranged in a succession in which there is a relationship or rule between each successive number.
• A sequence can be finite or infinite. A finite sequence has a last term, and an infinite sequence has no last term.
• The following is an example of a finite sequence:
{3, 6, 9, 12, 15, 18}
In this sequence, each number has a value of 3 more than the preceding number.
• The following is an example of an infinite sequence describing the function f(x) = 1/x:
{1/1, 1/2, 1/3, 1/4, 1/5, 1/6,…}
domain set is x = {1, 2, 3, 4, 5, 6,…} and the
range set is f(x) = {1/1, 1/2, 1/3, 1/4, 1/5, 1/6,…}
• For example, the Fibonacci sequence is an unending sequence where each term is defined as the sum of its two predecessors. The numbers in the Fibonacci sequence are called the Fibonacci numbers and have many applications, including the pattern of the spiral curve arrangement of the seed head of a sunflower. Following is the Fibonacci sequence:
{1, 1, 2, 3, 5, 8, 13, 21, 34, …}
• An arithmetic progression is a sequence in which the difference between successive terms is a fixed number, and each term is obtained by adding a fixed amount to the term before it. This fixed amount is called the common difference.
• Arithmetic progressions can be represented by first-degree polynomial expressions. For example, the expression n + 1 can represent an arithmetic progression.
• The first sequence example in the previous section is an arithmetic progression:
{3, 6, 9, 12, 15, 18}
This arithmetic progression is represented by:
n + 3
• A finite arithmetic progression can be expressed as:
a, a + d, a + 2d, a + 3d, a + 4d, a + 5d,…, a + (n – 1)d
a is the first term.
d is the fixed difference between each term.
a + (n – 1)d is the last term or “nth” term.
n = 1, a1 = a + (1 – 1)d = a
n = 2, a2 = a + (2 – 1)d = a + d
n = 3, a3 = a + (3 – 1)d = a + 2d
n = 4, a4 = a + (4 – 1)d = a + 3d
n = 5, a5 = a + (5 – 1)d = a + 4d
and so on.
• In the arithmetic progression on the previous page:
{3, 6, 9, 12, 15, 18},
a = 3 and d = 3.
Therefore,
for n = 1, a1 = 3,
for n = 2, a2 = 6,
for n = 3, a3 = 9,
and so on.
• A geometric progression is a sequence in which the ratio of successive terms is a fixed number, and each term is obtained by multiplying a fixed amount to the term before it. This fixed amount is called the common ratio.
• The terms in a geometric progression can be represented as:
a, ar, ar2, ar3, ar4, ar5, …, arn – 1
a is the first term.
r is the ratio between successive terms.
arn – 1 is the last term.
• Note that the ratio of successive terms is always r.
ar/a = r
ar2/ar = r
ar3/ar2 = r
• For example, consider the following geometric progression:
2, 4, 8, 16, 32,…
If a = 2 and r = 2
This geometric progression can be expressed as:
2, 2(2), 2(2)2, 2(2)3, 2(2)4,…, 2(2)n – 1
• A series is the sum of the terms in a progression or sequence. An arithmetic series is the sum of the terms in an arithmetic progression. A geometric series is the sum of the terms in a geometric progression. The notation used to express a series is sigma notation.
• The sigma notation that represents an arithmetic series is:
an is the sequence function.
m is the index of the last term that is added.
n represents the nth term.
• For example, to obtain the sum of the first three terms in the sequence an from n = 1 to n = 3, the sigma notation is:
• In the arithmetic progression {3, 6, 9, 12,…}, for the first three terms:
• To sum a large number of terms in an arithmetic progression, the following equation for the arithmetic series can be used:
(m/2)(a1 + am)
Where m represents the last term added.
• Apply the equation for the arithmetic series to the arithmetic progression {3, 6, 9}.
(3/2)(3 + 9) = (3/2)(12) = 18
• Sigma notation that represents a geometric series is:
a is the first term and a ≠ 0.
r is the ratio between successive terms.
m is the index of the last term added.
n represents the nth term.
arn – 1 is the last term.
• In the geometric progression {2, 4, 8, 16, 32,…}, the sum of the first three terms is:
2 + 4 + 8 = 14
• The sum of a large number of terms in a geometric progression can be represented by:
Where m represents the last term added and r is the ratio.
• Apply the equation for the geometric series to the geometric progression {2, 4, 8}.
• If the geometric series is infinite, m will approach infinity (∞), therefore, the limit as m approaches infinity of the expression of the series is:
If |r| < 1 and m → ∞, then rm approaches zero, and the sum of the infinite geometric series becomes:
(See the next section for proof.)
• A series is a sum of the terms in a progression or sequence. If the progression or sequence is infinite and therefore there is an infinite number of terms, then the sum cannot be calculated. However, under certain conditions the sum of an infinite series can be estimated.
• Conditions under which the sum of an infinite series can be estimated include the following.
If an infinite series has a limit, it is said to converge, and the sum can be estimated. In other words, as the terms in an infinite series are added, beginning with the first term, if with each additional term added the sum approaches some number, then the series has a limit and converges, and the sum can be estimated.
If an infinite series has no limit, it is said to diverge, and the sum cannot be estimated. In other words, if instead, as each additional term is added the sum approaches infinity, then the series has no limit and diverges, and the sum cannot be estimated.
Another condition for convergence is that, for the infinite series that follows:
an must approach zero as n approaches infinity.
Although this condition must occur for a series to converge, there are cases where this condition is true but the series still diverges.
• To estimate an infinite series, it must be determined whether the series has a limit and converges, and what happens to the sum as the number of terms approach infinity. For example, consider the infinite series describing the sum of an from n = 1 to n = ∞:
If this series has a limit and converges to L it can be written:
• The geometric series a + ar + ar2 + ar3 + ar4 + ar5 + … + arn – 1, converges when |r| < 1 and diverges when |r| ≥ 1.
The geometric series can be expressed as:
and the sum of the first m terms is:
As m approaches infinity:
If |r| < 1 and m→∞, then rm→0, resulting in:
Therefore, as m→∞, if |r| < 1, the series converges, and if |r| ≥ 1, it diverges.
• To determine whether a given series will converge, there are a variety of tests for convergence that may be used, including the Comparison Test, the Ratio Test, and the Integral Test. These three tests are discussed in the following section.
• Note: The limit is used in the estimation of infinite sums and the definition of the derivative in calculus. In general, the limit is used to describe closeness of a function to a value. For example, if the Limx→a f(x) = L, then it is said that the function f(x) gets close to and may equal some number L as x approaches and gets close to some number “a”. (Please refer to Chapter 5, “Limits.”)
• To determine whether an infinite series will converge, there are a variety of tests for convergence that may be used. These tests include the Comparison Test, the Ratio Test, the Integral Test, and tests for series with positive and negative terms.
• The Comparison Test can be applied to a series with positive terms.
A series is convergent if each term is less than or equal to each corresponding term in a series that is known to be convergent.
Conversely, if each term in an unknown infinite series is greater than or equal to each corresponding term in a known divergent infinite series, then the unknown infinite series is also divergent.
• An example of a known convergent series is the P Series:
1 + 1/2P + 1/3P + … + 1/nP + …
The P Series converges when P > 1 and diverges when P ≤ 1.
• A divergent series that is used as a comparison in the Comparison Test is:
1 + 1 + 1 + 1 + …
As the number of terms approaches infinity, the sum of the terms approaches infinity and the series diverges.
• Example: Will Series U converge?
U = 1 + 1/2 + 1/3 + … + 1/n + …
(This is called the Harmonic Series.)
Compare with the known Series K, which diverges as more terms are added.
K = 1 + 1/2 + 1/2 + 1/2 + …
To compare Series K to Series U rewrite Series K as:
K = 1 + (1/2) + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + …
Compare Series K to Series U term by term.
U = 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8…
Many of the terms in U are greater than the corresponding terms in K. Therefore, because K diverges, U must also diverge.
• This example is an interesting case because in the Harmonic Series, the value of the terms do approach zero, which is a necessary criteria for convergence but does not guarantee it. However, by applying the Comparison Test with a series that is known to diverge, it is clear that the Harmonic Series also diverges.
• The Ratio Test for convergence can be applied to a series of positive terms.
• To apply the Ratio Test for the series:
a1 + a2 + a3 + …an + …
Find the ratio of successive terms:
To determine r, take the Limit as n→∞:
If r < 1, the series will converge.
If r > 1, the series will diverge.
If r = 1, the test does not indicate convergence or divergence.
• The Ratio Test can be applied to evaluate convergence of series containing positive and negative terms.
• To apply the Ratio Test to an alternating series, take the Limit as n→∞ for the ratio of the absolute value of successive terms:
If r < 1, the series is absolutely convergent.
If r > 1, the series is divergent.
If r = 1, this test does not indicate convergence or divergence.
This series therefore may be absolutely convergent, conditionally convergent, or divergent.
• A series with positive and negative terms converges if the corresponding series of the absolute values of the terms converges.
If Series |S| converges then series S will converge.
|S| = |a1| + |a2| + |a3| + |a4| + |a5| + … |an| + …
and:
S = a1 + a2 + a3 + a4 + a5 + … an + …
an can be positive or negative.
• A series with positive and negative terms may converge and is called conditionally convergent, even though its corresponding series of absolute values diverges. For example:
1 – 1/2 + 1/3 – 1/4 + 1/5 – … converges conditionally.
1 + 1/2 + 1/3 + 1/4 + 1/5 … diverges.
• In an alternating series in which the signs of the terms alternate positive and negative:
a1 + a2 – a3 + a4 – a5 + a6 – a7 + … an + …
The alternating series will converge if the following conditions are true from some point in the series:
an ≥ an + 1 for all values of n, and each a is positive
Limn—∞ an = 0
Please refer to Chapter 7, “Introduction to the Integral,” for an explanation of integrals.
• The Integral Test can be applied to a decreasing series of positive terms in which an + 1 < an for all successive terms. To apply the Integral Test to a series, integrate the function representing the series. If the integral of the series exists and therefore converges, then the series also converges.
Consider the decreasing series:
an represents f(x).
If f(x) is a positive continuous function and:
f(x)dx exists and converges then: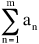
also converges.
• For example, apply the Integral Test to the series represented by f(x) = 1/x.
Integrate between 1 and ∞.
The integral of 1/x is ln x, (“ln” is the natural logarithm).
Because the integral from 1 to ∞ is infinity and does not exist, it diverges. Therefore, the series also diverges.
• The power series of x has the form:
an represents the constant coefficients.
x is the variable.
• A more generalized form of the power series is of (x – a):
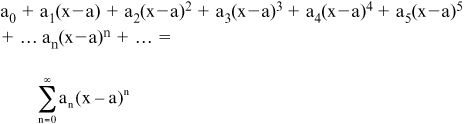
• For the power series:
The series in x converges if x = 0.
The series in (x – a) converges if x = a.
There is a positive number r such that the series converges if |x| < r and diverges if |x| > r.
• To evaluate convergence for other values of x for a given power series, the generalized Ratio Test can be applied (see previous section). For example, for the power series in x:
The power series converges when 
and diverges when 
and may or may not converge when
Note that the set of values of x for which the series is convergent is called the interval of convergence.
(See Chapter 5, “Limits,” for explanation of Limn→∞.)
• When a function is written in the form of an infinite series, it is said to be “expanded” in an infinite series. This series represents all values of x in the interval of convergence.
• For the function f(x), the infinite series is:
Or:
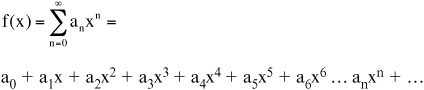
• The function f(x) has the following properties of a polynomial:
It is continuous within the interval of convergence (there is no break in its graph).
In series form, the function can be added, subtracted, multiplied, or divided term by term.
If f(x) is differentiable, then the series can be differentiated term by term (see Chapter 6, “Introduction to the Derivative”).
• Two common series representing expansions are the Maclaurin Series and the Taylor Series. In these series, successive derivatives are taken and the coefficients can be obtained. For a function f(x) expanded in a power series:
In the special case of a = 0:
f(x) = a0 + a1x + a2x2 + a3x3 + … anxn + …
Where, f(0) = a0.
Take the first derivative of each term (where ′ represents the derivative). (See Chapter 6, “Introduction to the Derivative.”)
f′(x) = a1 + 2a2x1 + 3a3x2 + … nanxn – 1 + …
Where, f′(0) = a1.
Take the second derivative of each term.
f″(x) = 2a2 + (2)3a3x + … n(n – 1)anxn – 2 + …
Where, f″(0) = 2a2.
Take the third derivative of each term.
f‴(x) = (2)3a3 + (2)(3)4a4x… n(n – 1)(n – 2)anxn – 3 + …
Where f‴(0) = 6a3.
Take the nth derivative of each term.
f(n)(x) = n!an + (n + 1)!an + 1x + …
(Remember “!” represents factorial.)
The coefficients are determined at x = a = 0:
a0 = f(0)
a1 = f′(0)
a2 = f″(0)/2
a3 = f″′(0)/(2)(3)
an = f(n)(0)/n!
Therefore, the expansion of f(x) is:
This is known as the Maclaurin Series, which is expanded about the point zero.
• In the Taylor Series, the function is expanded about point a rather than zero. f(x) is represented as:
f(x) = a0 + a1(x – a) + a2(x – a)2 + a3(x – a)3 + … an(x – a)n + …
The coefficients an are computed by repeated differentiation as with the Maclaurin Series. The expansion of f(x) is:
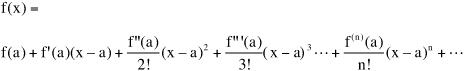
This is known as the Taylor Series, which is expanded about point a. When a = 0, the Taylor Series can be reduced the Maclaurin Series.
• Tables of exponential, logarithmic, and trigonometric functions are often obtained from computations by series. For example, the exponential function ex can be computed using the Maclaurin expansion.
= 1 + 1 + 0.5 + 0.166667 + 0.041667 + 0.008333 + 0.001389 + 0.000198 + … = 2.718254
Therefore, ex for x = 1 is approximately equal to 2.718254.
Also, trigonometric functions can be expanded and computed for selected values. For example:
• The binomial expression (a + b), can be expanded into polynomial form called the binomial expansion. (See Chapter 5, “Polynomials,” in the second book of the Master Math series, Algebra.)
• To expand (a + b) into (a + b)n:
First, consider the expansions for (a + b)2, (a + b)3, and (a + b)4:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
(a + b)3 = (a + b)(a + b)(a + b) = a3 + 3a2b + 3ab2 + b3
(a + b)4 = (a + b)(a + b)(a + b)(a + b) = a4 + 4a3b + 6a2b2 + 4ab3 + b4
(These expansions are obtained by multiplying the first two binomials, then multiplying each successive binomial with the preceding polynomial.)
For the expansion of (a + b)n, where n is a positive integer, the Binomial Theorem is applied as follows:
The rth term is given by:
