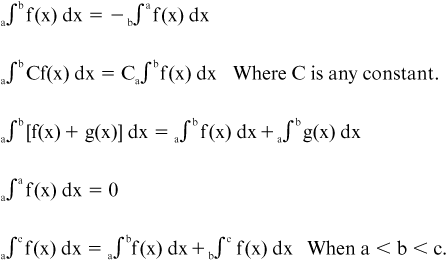7.1 Definition of the Antiderivative or Indefinite Integral
7.2 Properties of the Antiderivative or Indefinite Integral
7.3 Examples of Common Indefinite Integrals
7.4 Definition and Evaluation of the Definite Integral
7.5 The Integral and the Area Under the Curve in Graphs of Functions
7.6 Integrals and Volume
7.7 Even Functions, Odd Functions, and Symmetry
7.8 Properties of the Definite Integral
7.9 Methods for Evaluating Complex Integrals: Integration by Parts, Substitution, and Tables
• This section presents the antiderivative or indefinite integral, the formula for the antiderivative or indefinite integral, the comparison between the antiderivative and the derivative, and the added constant.
• The antiderivative or indefinite integral is approximately equal to the inverse of the derivative. The antiderivative or indefinite integral of a function f(x) is written:
∫ f(x) dx
∫ is the integral symbol and f(x) is called the integrand.
• If the derivative of the function f(x) is the function F(x):
Then the antiderivative of F(x) is f(x) plus a constant.
∫ F(x) dx = f(x) + c
c represents an arbitrary constant of integration and dx indicates integrate with respect to x.
• Remember the formula for the derivative:
• The formula for the antiderivative or indefinite integral is:
c represents a constant value and is called the constant of integration.
• A constant is added to the integral because the derivative of a constant is zero.
• Evaluate the derivative of the antiderivative formula using the derivative formula:
• Because the derivative is the rate of change of some function, it seems likely that several different functions could have the same rate of change. For example, calculate the derivatives of the following three functions:
Then, take the integral of 4x to illustrate that each function is different even though they all have the same rate of change (derivative):
Therefore, in the three functions, c represents 3, ![]() , and π.
, and π.
• In this section, the indefinite integral of a function multiplied by a constant, the sum of two functions, a polynomial function, repeated integration, and the integral of a constant are described.
• The indefinite integral of a function multiplied by a number is equal to the number multiplied by the indefinite integral of the function.
∫ 2f(x) dx = 2 ∫ f(x) d(x)
• The indefinite integral of a sum of functions is equal to the sum of the indefinite integrals.
∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx
• When taking the indefinite integral of a polynomial function, apply the integral formula term-by-term (as with differentiating).
∫(x3 + x2 + x) dx = ∫ x3 dx + ∫ x2 dx + ∫ x dx = [(1/4)x4 + c)] + [(1/3)x3 + c] + [(1/2)x2 + c]
Combining the c’s:
= (1/4)x4 + (1/3)x3 + (1/2)x2 + C
Where, C = c + c + c.
• The derivative is the rate of change of something (as discussed in Chapter 6). For example, the rate of change of distance x(t) is velocity v(t), and the rate of change of velocity v(t) is acceleration a(t).
 and
and 
Conversely, the integral of acceleration is velocity, and the integral of velocity is distance.
∫ a(t) dt = v(t) + c
∫ v(t) dt = x(t) + c
• Integration may be repeated any numbers of times. To take multiple integrals of a function, begin with the innermost integral.
For the case of distance = x(t), velocity = v(t), and acceleration = a(t), the double integral of acceleration is:
∫∫ a(t) dt dt = ∫ v(t) + c1 dt = x(t) + c1x + c2
For the case where the ∫ of f(x) is F(x), the ∫ of F(x) is g(x), and the ∫ of g(x) is G(x), then the triple integral of f(x) is:
• The integral of a constant alone is equal to the constant c multiplied by the variable (in this case x) that the constant is being integrated with respect to (indicated by dx), plus another constant. For example:
∫ c1 dx = c1x + c2
• The following integrals are commonly used in calculus:
• In this section, the Fundamental Theorem of Calculus, the integral formula for the definite integral, the definite integral of a function multiplied by a constant, the sum of two functions, improper integrals, and repeated integration are described.
• By the Fundamental Theorem of Calculus, if f is a continuous function between points x = a and x = b, and f′(x) is the derivative of f(x), then:
 f′(x) dx = f(b) – f(a)
f′(x) dx = f(b) – f(a)
And if F is the antiderivative of f, or F′ = f(x), then, the definite integral of f(x) between x = a and x = b is:
 f(x) dx = F(b) – F(a)
f(x) dx = F(b) – F(a)
And the indefinite integral of f(x) is:
∫ f(x) dx = F(x) + c
• Definite integrals are evaluated at the values given at the ends of the ∫ symbol called the limits of integration.
Above, F(x) is evaluated at x = b and x = a.
The symbol for evaluated at a and b is ![]() and it describes subtraction of the function at the top value minus the function at the bottom value:
and it describes subtraction of the function at the top value minus the function at the bottom value:
• Example: Find the area of the function f(x) = x2 between x = 0 and x = 1 by applying the integral formula and evaluating at the two x boundaries or limits of integration. (See the next section for a discussion on the area under a curve on a graph of a function.)
• The integral formula for the definite integral bounded by limits of integration, x = a and x = b, is written:
• When the definite integral is evaluated, it is not necessary to add a constant.
• The following two rules for the definite integral of a function multiplied by a constant and the definite integral of a sum of functions that applied to indefinite integrals also apply to definite integrals:
 Cf(x) dx = C
Cf(x) dx = C  f(x) dx
f(x) dx
Where C is any real number.
 [f(x) + g(x)] dx =
[f(x) + g(x)] dx =  f(x) dx +
f(x) dx +  g(x) dx
g(x) dx
• A definite integral is called an improper integral if the integrand is infinite or becomes infinite between its limits, or if one or both of the limits of integration are infinite. An improper integral is discontinuous or diverges at one or more points in the function between the limits of integration.
• Integration may be repeated any number of times. To take multiple integrals of a function, begin with the innermost integral and evaluate it at the limits of integration for the inside integral, then take the integral of the result and evaluate it at the next innermost limits of integration. Repeat this for the number of integrals specified by the number of ∫ symbols.
• To evaluate the following double integral of the function f(x), take the integral of f(x) and evaluate it at the limits of c and d, then take the integral of the result and evaluate it at the limits of a and b.
 f(x) dx dx
f(x) dx dx
• One application of the integral is that it can be used to define the area under a curve on a graph of a function. To use the integral to define the area under some region of a curve between points x = a and x = b, the curve in this region must be continuous and not extend into a vertical asymptote. Consider the following graph of function f:

The striped pattern represents the area under the curve of function f. The area under the curve of f between x = a and x = b is given by:
 f(x) dx
f(x) dx
This is called the definite integral of f between x = a and x = b.
• In the interval between x = a and x = b on the graph of f(x), the X-axis can be divided into n equal parts of width Δx, such that the Δx segments extend from the X-axis to the f(x) curve so that the area is divided into vertical rectangular strips. (Note that Δ represents some small change in x.)

Between x = a and x = b, there are n rectangular strips and each strip is called the ith strip. The width of each strip is Δx and the height of each strip is yi. The area of each strip is width times height, given by:
(yi)(Δx) or (f(xi))(Δx)
An approximation for the total area of f(x) between x = a and x = b is the sum of the areas of the n strips, which can be written:
Or equivalently:
If the width of Δx shrinks and the number of n strips increases, the sum of the strips will represent a better approximation of the actual area. This can be written:
Also, note that Δx can be equivalently written ![]() .
.
Therefore, the area approximation can be written:
The area bound by x = a and x = b is also given by the definite integral and is written:
Area =
 f(x) dx
f(x) dx
This is approximately equal to:
• In functions with part of the curve below the X-axis, the area between the X-axis and the curve is negative in value and subtracts from the area above the X-axis.

The graph of y = f(x) between x = –a and x = a is given by:
 f(x) dx = area A + area B + area C + area D
f(x) dx = area A + area B + area C + area D
Area B and area D are negative in value.
• If the area below the curve is equal to the area above the curve, the resulting integral is equal to zero.
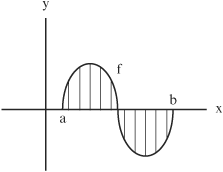
The graph of f between x = a and x = b is given by:
 f(x) dx = positive region + negative region = 0
f(x) dx = positive region + negative region = 0
The positive region is equal to the negative region.
• This section will present integrals that define the volume of an object. For a detailed discussion of this subject, Master Math: Calculus should be consulted.
• One application of the integral is to define the volume of an object. Volume can be defined by single integral equations, double integral equations, and triple integral equations.
• In the graph of a non-negative continuous function, the area under the curve of function y = f(x) is given by ![]() f(x) dx. If the function is revolved about the X-axis between x = a and x = b, a volume is generated. This volume is called the volume of revolution. The area of a vertical cross-section of the volume is πy2 and the volume of a section that has a thickness of dx is πy2dx. The volume of the volume of revolution between two vertical planes at x = a and x = b is given by:
f(x) dx. If the function is revolved about the X-axis between x = a and x = b, a volume is generated. This volume is called the volume of revolution. The area of a vertical cross-section of the volume is πy2 and the volume of a section that has a thickness of dx is πy2dx. The volume of the volume of revolution between two vertical planes at x = a and x = b is given by:
V = π
 [f(x)]2 dx or V = π
[f(x)]2 dx or V = π  y2 dx
y2 dx
• In the graph of a non-negative continuous function between x = a and x = b, the volume can be described using the method of cylindrical shells. The area bounded by x = a and x = b is revolved about the Y-axis generating a volume. If this volume is divided along the X-axis into n parts each having a thickness of Δx, n vertical cylinders will result. The volume of each shell is obtained by subtracting the volume of a smaller cylinder from the next larger one, πR2h – πr2h = πh(R2 – r2), where R is the radius of the larger cylinder and r of the smaller, and h is the length along the Y-axis. If the sum of the n shells is taken, as n approaches infinity and the thickness of each shell approaches zero, the volume is described by:
V =
 2πhx dx
2πhx dx
• If the volume of an object is divided into columns in the direction of the Z-axis in an XYZ coordinate system, where the volume of each column is F(x, y) dy dx, then the sum of all the columns gives the total volume for the continuous function F(x, y) and is described by:
V =
 F(x, y) dy dx
F(x, y) dy dx
• If the volume of an object is divided into cubes in an XYZ coordinate system so that the volume of each cube is dx dy dz, then the sum of all the cubes gives the total volume and is described by:
• By determining whether a function is even or odd, it is often possible to simplify the integral of the function to a more manageable form and solve using symmetry.
• A function is even if f(x) = f(–x) between x = –a and x = a. An example of a graph of an even function is:

From the graph, it is clear by symmetry that the section on the left of the Y-axis, between x = –a and x = 0, is equivalent to the section on the right of the Y-axis, between x = 0 and x = a.
The integral for this even function can be written:
In an even function, the area for negative values of x is equal to the area for positive values of x.
• Examples of even functions are:
f(x) = c
f(x) = x2
f(x) = x4
f(x) = x2n
Note: f((–x)2) = (–x)(–x) = x2.
• A function is odd if f(x) = –f(–x) between x = –a and x = a. An example of a graph of an odd function is:

From the graph, it is clear by symmetry that the section on the left of the Y-axis, between x = –a and x = 0, is equivalent but opposite to the section on the right of the Y-axis, between x = 0 and x = a.
The integral for this odd function can be written:
The area for negative values of x is equal but opposite to the area for positive values of x, and the two areas subtract and cancel each other out, resulting in an integral equivalent to zero.
• Examples of odd functions are:
f(x) = x
f(x) = x3
f(x) = x5
f(x) = x2n + 1
Note: f((–x)3) = (–x)(–x)(–x) = (–x)3
• To evaluate complicated integrals, methods that go beyond simply applying the integral formula are often required. Some of the most common methods are integration by parts, substitution, and looking up integrals in integral tables.
• To evaluate certain complicated integrals, the method of integration by parts can be applied. To use this method, the integral must exist in the form or be arranged to fit the form of the following formula:
∫ f(x) g′(x) dx = f(x) g(x) –∫ f′(x) g(x) dx
Using other notation, where u = f(x) and v = g(x), the formula is written:
∫ u dv = uv – ∫ v du
• In the following example, integration by parts can be used to solve the integral:
∫ x cos x dx
To arrange this integral in a form that will fit the integration by parts formula, make the following substitutions:
u = x
du = dx
dv = cos x dx
From the substitution for dv, v = ∫ cos x dx = sin x.
Using the integration by parts formula:
∫ u dv = uv – ∫ v du
The integral becomes:
∫ x cos x dx = x sin x –∫ sin x dx
Because ∫ sin x dx = –cos x, the evaluated integral becomes:
∫ x cos x dx = x sin x + cos x + c
• Substitution of variables is used to translate a complicated integral into a more manageable form so that the integral can be solved using the integral formula or integral tables, then the integral is translated back to its original variables. For example, given the function:
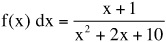
The integral is

First, simplify the integral by substituting:
u = (x2 + 2x + 10)
Where the derivative of u is:
du = (2x + 2) dx = 2(x + 1) dx
Rearranging to isolate dx gives:
dx = du / 2(x + 1)
Next, substitute u and du into the integral so that (x2 + 2x + 10) = u and dx = du / 2(x + 1), then evaluate the integral.
(Remember, ∫ 1/x dx = ln |x| + c.)
Finally, substitute the original expressions back into the evaluated integral, where u = (x2 + 2x + 10).
= (1/2) ln |(x2 + 2x + 10)| + c
Therefore,
∫ (x + 1)/(x2 + 2x + 10) dx = (1/2) ln |(x2 + 2x + 10)| + c
• There are many advanced techniques for solving complex integrals that can be found in calculus textbooks and handbooks of mathematical functions. Integral tables are useful for solving integrals in forms that do not allow easy application of integration techniques. Integral tables are found in mathematical handbooks, calculus books, on-line integral tables and resources, and the CRC Handbook of Chemistry and Physics.
• Integral tables contain solved integrals in various forms so that an unknown integral can be matched to, or translated into, the form in the integral table that is identical or most similar to it. If the unknown integral is not identical to a form in the table, a transformation of the integral must be made using substitution, for example, substitute y for ax. Specific substitutions are suggested within integral tables for certain integrals. In general, when making substitutions, it is important to make a substitution of the dx terms, to express the limits of the definite integrals in the new dependent variable, and to perform reverse substitution to obtain the answer in terms of the original independent variable for indefinite integrals.
It may be helpful to peruse some integral tables and on-line resources to become familiar with the integrals and substitution suggestions, and to read the introductory discussions at the beginning of the tables.