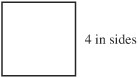• Different lines and angles have specific names according to their environment, position, size, measurement, etc. This section provides some common definitions for lines and angles.

• The shortest distance between two points is a straight line. The distance between points (x₁, y₁) and (x₂, y₂) is given by:

The coordinates of the midpoint between the two points are:

• A line segment is a section of a line between two points.

There are three line segments in the above line:

Segment AB, Segment BC, and Segment AC.

• A ray has an end point at one end and extends indefinitely in the other direction.

• If two straight lines meet or cross each other at a point, an angle is formed. The point where the lines meet is called the vertex of the angle and the sides are called the rays of the angle.

The vertex is at point A and the rays are AB and AC.

• The symbol for an angle is ∠. The above angle can be called ∠ BAC (where the middle letter names the vertex) or simply ∠ A.

• Angles are measured in degrees or radians. The symbol for degrees is °, and radian is often shortened to rad.

• A 180° angle is a straight line.

∠ ABC = 180°

• The symbol for a right angle or a 90° angle is a square drawn at the vertex.

• Angles smaller than 90° are called acute angles.

• Angles larger than 90° are called obtuse angles.

• If two angles have the same vertex and are adjacent to each other, they are called adjacent angles.

∠ a and ∠ b are adjacent angles.

• If the sum of any two angles equals 180°, the two angles are called supplementary angles. The following examples are of angles that are adjacent and supplementary. Note that supplementary angles do not have to be adjacent.

Where a° + b° = 180°.

• If the sum of any two angles equals 90°, the two angles are called complementary angles. For example, if ∠ ABC is a right angle, then angles ∠ ABD and ∠ DBC are adjacent and complementary angles. Note that complementary angles do not have to be adjacent.

• If two lines intersect each other, there are four angles formed.

The sum of the four angles is 360°.

The sum of the adjacent angles is 180°.

The angles opposite to each other are called vertical angles and they are equivalent.

• If two lines are perpendicular to each other, four right angles, each measuring 90°, are formed.

• A transversal is a line that intersects two other lines.

If lines A and B are parallel to each other, the following is true:

• As described later in the circle section, there are:

• A polygon is a closed planar figure that is formed by three or more line segments that all meet at their end points, and there are no end points that are not met by another end point. The line segments that make up a polygon only intersect at their end points.

• Examples of polygons are:

Note that rectangles, squares, and trapezoids are also quadrilaterals.

• Polygons are named according to the number of sides they have. For example:

Number of Sides and Name

3 = Triangle

4 = Quadrilateral

5 = Pentagon

6 = Hexagon

7 = Heptagon

8 = Octagon

9 = Nonagon

10 = Decagon

• In a polygon, the number of sides equals the number of angles.

• Polygons are often referred to by labels or letters written at their angles. For example, the following quadrilateral can be referred to as ABDC:

• If the length of the sides are equal and the angle measurements are equal, the polygon is called a regular polygon. A square is a regular quadrilateral.

• If two polygons have the same size and shape, they are called congruent polygons.

• If two polygons have the same shape such that their angle measurements are equal and their sides are proportional, however one is larger than the other, they are called similar polygons.

• The following equation gives the sum of all the angle measurements in a polygon:

• For example, if a quadrilateral has four sides and four angles, what is the sum of all angle measurements?

Therefore, the sum of the angles in a quadrilateral is 360°.

• Triangles are three-sided polygons. The symbol for a triangle is Δ.

• The sum of the angles of a triangle is:

For a triangle, n = 3,

Therefore, the sum of the angles of every triangle is 180°.

• If the value of two angles in a triangle is known, the third angle can be calculated by subtracting the sum of the two known angles from 180°.

• The length of one side of a triangle is always less than the sum of the other two sides.

• In a triangle, the largest side is opposite the largest angle, the smallest side is opposite the smallest angle, and the middle-length side is opposite the middle-size angle.

• Examples of triangles are:

• In an equilateral triangle, all three sides have equal lengths and all three angles have equal measurements of 60°. The sum of the angles in an equilateral triangle is: 60° + 60° + 60° = 180°.

• In an isosceles triangle, two sides have equal lengths and the angles opposite the two equal sides have equal measurements.

• In a scalene triangle, all three sides have different lengths and all three angles have different measurements.

• If one of the angles in the triangle is a right angle (90°), the triangle is called a right triangle.

• If all of the angles in a triangle are smaller than 90°, the triangle is called an acute triangle.

• If one of the angles in the triangle is larger than 90°, the triangle is called an obtuse triangle.

• In a right triangle, the side opposite to the right angle is called the hypotenuse and the two sides that meet to form the right angle are called legs. The hypotenuse is always the longest side.

• In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.

This is called the Pythagorean Theorem and it only applies to right triangles.

If the lengths of the legs are x and y and the length of the hypotenuse is z, the Pythagorean Theorem can be written:

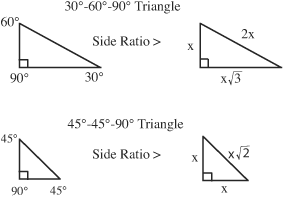
• Two noteworthy right triangles are the 30°-60°-90° and the 45°-45°-90° (right isosceles triangle).

• Other noteworthy right triangles are called triplets. The most common triplets are 3:4:5, 5:12:13, and 7:24:25.

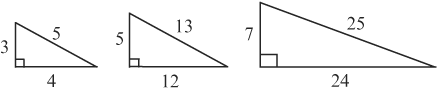
Note that any multiple of the ratios of these triangles is also a triplet, such as 6:8:10, 10:24:26, etc.

• If two corresponding angles of two triangles are equal, then the third angles are also equal.

• If two corresponding sides of two right triangles are equal, the third corresponding sides are also equal and the triangles are congruent. This can be proven using the Pythagorean Theorem.

• Two triangles are called congruent triangles if:

(Slash marks indicate same length.)

• If all three pairs of corresponding angles in two triangles are equal to each other, the two triangles are called similar triangles. Two similar triangles can be created by drawing a line parallel to one of the sides of a triangle.

ΔADC is similar to ΔAEB because three corresponding angles are equal.

• In this section, various types of quadrilaterals including parallelograms, rhombuses, rectangles, squares, and trapezoids are described.

• Quadrilaterals are four-sided polygons.

• The sum of the angles in a quadrilateral is:

The sum of the angles in all quadrilaterals is 360°.

• A parallelogram is a quadrilateral with both of the two opposite sides parallel to each other.

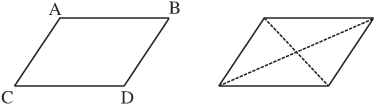
AB is parallel to CD. AC is parallel to BD. Both pairs of opposite sides are the same length. Both pairs of opposite angles are the same size. If diagonal lines (shown dashed above) are drawn to either pair of opposite angles the resulting triangles are congruent.

• A rhombus is a parallelogram with all four sides of equal length.

(Slash marks indicate same length)

Opposite angles of a rhombus are equal to each other. Diagonal lines (shown dashed above) drawn in a rhombus are perpendicular to each other.

• A rectangle is a parallelogram with all four angles having equal measurements of 90°.

Opposite sides of a rectangle are also equal to each other. Diagonal lines (shown dashed above) drawn in a rectangle are the same length. The length of the diagonal lines can be determined using the Pythagorean Theorem if the side lengths of the rectangle are known.

(long-side length)² + (short-side length)² = (diagonal length)²

• A square is a parallelogram in which the four angles and four sides are equal.

The angles will each measure 90°. Diagonal lines (shown dashed above) drawn in a square are the same length. The length of the diagonal lines can be determined using the Pythagorean Theorem if the side lengths of the square are known.

For example, if the side length is x and the diagonal length is d:

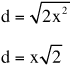
• A trapezoid is a quadrilateral having only one pair of opposite sides parallel to each other.

AB is parallel to CD. AC is not parallel to BD. AB and CD are called bases. AC and BD are called legs.

• In this section, the following terms are defined: circle, radius, diameter, chord, Pi, degree, radian, tangent, concentric, central angle, inscribed angle, and arc.

• A circle is a planar shape consisting of a closed curve in which each point on the curve is the same distance from the center of the circle.

C denotes the center of the circle.

• The radius of a circle is the distance between the center and any point on the circle. All radii drawn for a given circle have the same length.

• A line segment drawn through the center point with its end points on the circle is called the diameter of the circle. The diameter is twice the radius.

A diameter line divides a circle into two equal semicircles.

• Any line segment whose ends are on the circle is called a chord (including the diameter line segment).

X depicts the point at the center of the circle. AB is the diameter chord. CD is a chord. XE, AX, and XB are radii.

• Pi, or π, defines the ratio between the circumference and the diameter of a circle. More specifically, Pi is equivalent to the circumference divided by the diameter of a circle.

• The value of Pi is approximately 3.141592654.

• The degrees of a circle are:

2π radians = 360 degrees.

1 radian = 360°/2π = 180°/π.

1 degree = 2π radians/360° = πradians/180°.

Because there are 360° in a circle: 1° = 1/360.

1 Minute is defined as (′) = (1/60) of 1°.

1 Second is defined as (″) = (1/60) of 1 Minute.

• A circle always measures 360° around, equivalent to 2π radians. Half of the circle measures 180°, which is equivalent to π radians. A quarter of a circle measures 90°, which is equivalent to π/2 radians.

• A tangent line passes through only one point on a circle. If a radius line segment is drawn from the center of the circle to the point of tangency, the tangent line and the radius line segment are perpendicular to each other.

• If two or more circles have the same center point they are called concentric circles.

• If angles or polygons are drawn inside circles, any angle whose vertex is at the circle’s center point is called a central angle.

• If angles or polygons are drawn inside circles, any angle whose vertex is on the circle is called an inscribed angle.

• A section of a circle defined by two or more points is called an arc. An arc can be measured in degrees or radians. (There are 2π radians in 360° and π radians in 180°.)

For example, if r = 10, d = 20, n = 90° =π/2 radians,

• The measure of a central angle is equal to the measure of the arc it intercepts.

∠ ABC = Arc AC

Note the following relationship for central angles:

• A central angle subtending an arc equal in length to the radius of a circle is defined as a radian. One radian is approximately 57.29578 degrees. (Subtend means to extend under or be opposite to.)

• The measure of an inscribed angle is equal in measure to half of the arc it intercepts.

∠ ABC (1/2)(Arc AC)

• If an inscribed angle has its rays ending at the end points of a diameter chord, the vertex of the angle will be a right angle (90°), (which is one-half of the 180° measurement of the arc).

∠ ABC = 90° = (1/2)(Arc AC) = (1/2)180°.

• Inscribed angles with the same endpoints defined by the same arc, have the same measure.

• An inscribed angle is equal to one-half of the central angle formed from the endpoints of the same arc.

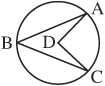
Angle ABC is an inscribed angle with endpoints on arc AC. Angle ADC is a central angle with endpoints on arc AC. Because they are formed by the same arc, angle ABC is one-half the measure of angle ADC.

• Measuring perimeter and area of two-dimensional objects including triangles, squares, rectangles, regular hexagons, circles, parallelograms, and trapezoids are described in this section.

• The perimeter of polygons and planar figures such as circles is the sum of the lengths of its sides or the distance around something. The units for perimeter are always singular because of the one-dimension described. Remember to convert all measurements to the same units before adding.

• The following are examples of perimeter measurements.

Triangle

Perimeter of a triangle is the sum of the sides:

2 inches + 3 inches + 4 inches = 9 inches

Square

Perimeter of a square is the sum of the sides:

2 inches + 2 inches + 2 inches + 2 inches

= 4(2 inches) = 8 inches

Rectangle

Perimeter of a rectangle is the sum of the sides:

2 inches + 2 inches + 4 inches + 4 inches

= 2(2 inches) + 2(4 inches) = 12 inches

Regular Hexagon

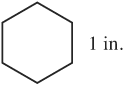
Perimeter of a hexagon is the sum of all the sides:

1 inch + 1 inch + 1 inch + 1 inch + 1 inch + 1 inch

= 6(1 inch) = 6 inches

Circle

(The perimeter of a circle is called the circumference.)

Perimeter of a circle = circumference = 2πr = πd

= 2π2 inches = 4π inches ≈ 12.56 inches

Where, r = radius, d = diameter, and π ≈ 3.14.

• The area of polygons and planar figures, such as circles, is a measure of the planar dimensional space that the figure occupies. The units for area are always squared because of the two dimensions described, (x)(x) = x². Remember to convert all measurements to the same units before calculating.

• The following are examples of area measurements.

Triangle

Area of a triangle = (1/2)(base)(height) = (1/2)(6 inches)(3 inches) = 9 inches² or 9 square inches

To obtain the height, draw a line perpendicular from the base to the opposite angle.

Square

Area of a square = (side length)²

= (4 inches)² = 16 inches² or 16 square inches

Rectangle

Area of a rectangle = (length)(height)

= (6 feet)(2 feet) = 12 feet² or 12 square feet

Parallelogram

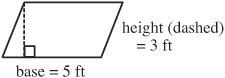
Area of a parallelogram = (base)(height)

= (5 feet)(3 feet) = 15 feet² or 15 square feet

To obtain the height, draw a line perpendicular from the base to the opposite angle.

Trapezoid

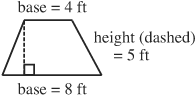
Area of a trapezoid = (average of bases)(height)

= (4 feet + 8 feet)/(2) × (5 feet)

= (6 feet)(5 feet) = 30 feet² or 30 square feet

To obtain the height, draw a line perpendicular from the base to the opposite angle.

• To find the area of polygons that are not triangles, squares, rectangles, parallelograms, or trapezoids, find the area of sections of the polygon that form one of these figures, then add the areas of the sections.

Circle

Area of a circle = πr² = π(d/2)²

= π(2 inches)² = π4 inches² ≈ 12.56 square inches

Where r = radius, d = diameter, and π ≈ 3.14.

The area of a sector of a circle is a fraction of the area of the whole circle. For a circle with its central angle = ABC:

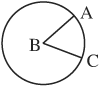
The following relationship is true:

If B = 60°, then the central angle is 60/360, or 1/6 of the circle. Also, the length of arc AC is 1/6 of the circumference of the circle. Finally, the area of sector BAC is 1/6 of the area of the circle.

• In this section, measuring volume, surface area, and main diagonal of three-dimensional objects including cubes, rectangular solids, cylinders, spheres, ellipsoids, cones, and pyramids are described.

• Volume is a measure of the three-dimensional space that an object occupies. The units for volume are always cubed because of the three dimensions described (x)(x)(x) = x³. Remember to convert all measurements to the same units before calculating.

• The surface area of three-dimensional objects such as cubes, rectangular solids, cylinders, and spheres is a sum of the areas of the surfaces. The units for surface area are always squared because of the two dimensions described, (x)(x) = x². Remember to convert all measurements to the same units before calculating.

• The following are examples of volume, surface area, and main diagonal measurements.

Cubes have six surfaces that are each squares and have the same measurements.

Volume of a cube = (edge)³

= (6 inches)³ = (6 inches)(6 inches)(6 inches)

= 216 inches³ or 216 cubic inches

Surface area of a cube = (6 sides)(area of each side)

= (6 sides)((6 inches)(6 inches)) = (6 sides)(36 inches²)

= 216 inches² or 216 square inches

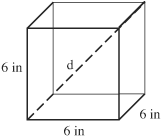
The main diagonal of a cube is given by:

s² + s² + s² = 3s² = d²

Where s = the length of the edge.

Rectangular solids have six rectangular surfaces with three pairs of opposite surfaces that have the same measurements.

Volume of a rectangular solid

= (length)(width)(height)

= (8 in.)(2 in.)(3 in.) = 48 inches³ or 48 cubic inches

Surface area of a rectangular solid

= (2)(length)(width) + (2)(length)(height) + (2)(width)(height)

= (2)(8 in.)(2 in.) + (2)(8 in.)(3 in.) + (2)(2 in.)(3 in.)

= (2)(16 in.²) + (2)(24 in.²) + (2)(6 in.²)

= (32 in.²) + (48 in.²) + (12 in.²) = 92 in.² or 92 square inches

Main diagonal of a rectangular solid is given by:

Cylinders or circular solids are three-dimensional objects that have two identical circles connected by a tube.

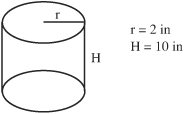
Volume of a cylinder or circular solid

= (area of circle)(height) = (πr²)(h)

= (π)(2 inches)²(10 inches) = (3.14)(4 inches²)(10 inches)

= 125.6 inches³ or 125.6 cubic inches

Surface area of a cylinder or circular solid

= (area of both circles) + (area of tube) 2πr² 2πrh

(where 2πr = circumference)

= (2)(π)(2 inches)² + (2)(π)(2 inches)(10 inches)

= (2)(3.14)(4 inches²) + (2)(3.14)(20 inches²)

= 25.12 in.² + 125.6 in.² = 150.72 in.² or 150.72 square inches

• Note: Pi is approximately equal to 3.1415926535897932384626433832795… and often abbreviated 3.14.

Spheres or spherical solids are three-dimensional objects consisting of points that are all the same distance from the center.

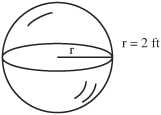
Volume of a sphere = (4/3)πr³

= (4/3)(π)(2 feet)³ = (4/3)(3.14)(8 feet³)

= 33.49 feet³ or 33.49 cubic feet

Surface area of a sphere = 4πr²

= 4π(2)² = 4(3.14)(2 ft.)² = 50.24 feet² or 50.24 square feet

The equation for the surface of a sphere drawn in the center of a coordinate system is:

x² + y² + z² = r²

Ellipsoids are oval-shaped, three-dimensional objects.

The equation for the surface of an ellipsoid drawn in the center of a coordinate system is:

Cones are three-dimensional objects that have a circle connected to a point. The depth of a cone forms a triangular solid.

Volume of a cone

= (1/3)(area of circle)(height) = (1/3)πr²d

Note that the volume of a cone is one-third the volume of a cylinder of the same radius and height.

Pyramids are three-dimensional objects that have a square, rectangle, triangle, or other polygonal base connected to a point.

Volume of a pyramid

= (1/3)(area of base)(height) = (1/3)(area of base)(d)

Remember, the area of a triangle is (1/2)(base)(height), the area of a square is (side)², and the area of a rectangle is (length)(height).

• Scalars represent quantities that can be described by one number (either positive, negative, or zero). However, vectors represent quantities that must be described by a numerical value and a direction. Examples of scalars are temperature and mass. Examples of vectors are velocity and force.

• Vectors are represented as a line with an arrow pointing in one direction. For example, the following depicts a vector:

• Vectors that point in the same direction and have the same length are equivalent.

• To add vectors, position the vectors so that the beginning (initial point) of the second vector is at the end (final point) of the first vector. The sum of the two vectors will be a third vector with its initial point at the initial point of the first vector and its final point at the final point of the second vector.

• Example: Add vectors a and b in the following two examples.

In the first example, put the initial point of b at the final point of a. The sum is the vector joining the initial point of a to the final point of b, or vector c.

In the second example, the initial point of b is already at the final point of a. The sum is the vector joining the initial point of a to the final point of b, or vector c.

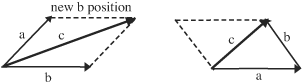
Both examples represent a + b = c

Note that the sum is also the diagonal of a parallelogram that can be constructed on a and b.

• Subtraction of two vectors is equivalent to addition of the first with the negative of the second vector.

• The negative of a vector is a vector with the same length but pointing in the opposite direction.

• To subtract two vectors, reverse the direction of the second vector, then add the first vector with the negative of the second vector by positioning the vectors so that the initial point of the (negative) second vector is at the final point of the first vector. The sum of the two vectors will be a third vector with its initial point at the initial point of the first vector and its final point at the final point of the second (negative) vector.

This example represents a – b = c