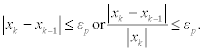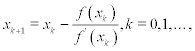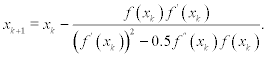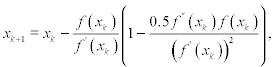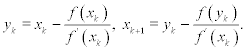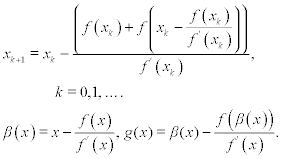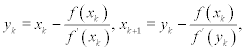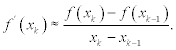Solving Nonlinear Equations
Finding a solution for an equation of the form f(x) = 0 is a frequently-encountered problem. It is not as easy to find roots of this equation as it might at first appear. Exact solutions are only possible if f(x) is a polynomial of degree n ≤ 9. By “exact solution,” we mean there is some procedure to calculate a root by using the parameters of the equation (as in the equation ax2 + bx + c = 0). In what follows, the term “root of an equation f(x) = 0” will be used interchangeably with “zero of f(x)”.
The root finding procedure is based on an iterative process or, in other words, on a process of successive approximations. An iterative process has four stages:
1. Root localization – that is, finding an interval which contains the only root.
2. Choosing an initial value, x0, or, in other words, letting x0 be an approximate value of x*.
3. Employing some procedure k times to obtain a set of approximations xk, starting from x0.
4. Finding out how close every approximation, xk, is to the exact solution (in terms of prescribed accuracy εp). If some approximation is in the εp-neighborhood of x*, then the iterative process is complete.
The last point will be satisfied only if:
that is, approximations xk converge to x*. That is why a great deal of attention will be given to conditions wherein an iterative process converges.
7.1 Calculation of Roots with the use of Iterative Functions
In what follows, we will consider another approach to calculate roots. An equation f(x) = 0 may be represented in the following equivalent form:
where g(x) is an iterative function. Thus, f(x*) = 0 is consistent with x* = g(x*). It turns out that form (7.1) is more appropriate for the construction of iterative algorithms. An iterative process is constructed in the following manner: let us set the value of x0 and the succeeding approximations will be calculated by the formula
Figure 7.1 shows the geometrical interpretation of the convergent iterative process (7.2).

Figure 7.1 Successive approximations generated by iterative scheme (7.2): a) g′(x) > 0 and b) g′(x) < 0.
The following theorem explains conditions which provide convergence of the iterative process (7.2).
One can derive an estimate of the error of the kth approximant, which depends only on the two successive approximants and the Lipschitz constant. Because |xk + 1 − xk| = |g(xk) − g(xk − 1)|, we can conclude from the Lipschitz condition that for all k, |xk + 1 = xk| ≤ L|xk − xk − 1|. Then
This gives us a bound on the error of the kth approximant. It should be noted that if L is close to one, convergence is very slow. So, a good part of our effort will be concentrated on how to construct an iterative process which converges rapidly.
There are a lot of methods for solving an equation f(x) = 0. We will consider only basic approaches. The iterative processes to be considered may be categorized as follows:
where β1(x), …, βn(x) are some functions.
Now, the term “rapid convergence” should be explained in more detail. To do this, we take the iterative process (7.4) as an example. To begin with, let us introduce the error of kth approximation as ek = xk − x *, then xk = x * + ek and xk + 1 = x * + ek + 1. After substituting these expressions in the iterative process (7.4), we can expand g(x* + ek) in terms of ek in the neighborhood of x* (assuming that all derivatives of g(x) up to order p are continuous):
Taking into account that x* = g(x*) we arrive at
If g(n)(x*) = 0 for n = 1, …, p − 1 and g(p)(x *) ≠ 0, then an iterative function, g, has an order, p, and thus it follows immediately from equation (7.7) that
where p is called the order of the sequence {xk} and C is called the asymptotic error constant. When p = 1, an iterative sequence has linear convergence to x*, while with p > 1, convergence is superlinear. It is clear that if ek is sufficiently small, then with p > 1 an iterative sequence may converge very rapidly.
Next, we need to discuss how to estimate how closely the kth approximation approaches the exact solution x*. To do this, we can use inequality (7.3). If xk ∈ [x * − εp, x * + εp], then the following conditions are fulfilled for absolute and relative error estimation, respectively:
In addition to conditions (7.9), usually another condition must be satisfied
This condition follows from the formulation of the problem. Therefore, an iterative process is finished when one of those conditions is fulfilled.
7.1.1 One-point iterative processes
To begin with, we will consider the case when g′(x *) ≠ 0. Then, as it follows from equation (7.7) that ek + 1 = g′(x *)ek and with the proviso that
convergence is linear. In practice, one cannot use condition (7.10), but we can require that the following condition be satisfied:
In this case, theoretical condition (7.10) is also satisfied. The simplest way to represent a source equation in form (7.1) is as follows:
and the associated iterative scheme is
This is the method of fixed-point iteration. In order that condition (7.11) is satisfied at every point in I, we should determine parameter α as follows:
To be more specific, we can choose
The initial value x0 should be chosen from interval I.
Convergence of the method of fixed-point iteration is not very rapid, but there is a procedure to decrease the number of iterations using the same information. Expression (7.7) for method (7.13) can be written as
Let us consider two consecutive iterations:
After eliminating R, we can express x* from those two expressions
If we take zk + 1 as an approximation to x*, then the accuracy of this approximation is O((ek)2) – that is, the sequence {zk} has convergence of the second order, as opposed to the sequence {xk} which has linear convergence. The transformation {xk} → {zk} is called Aitken’s δ2-process.
There are a lot of procedures to achieve superlinear convergence. Let the derivatives of f(x) up to order s be continuous in I. Then, in the neighborhood of xk∈ I, f(x) can be represented as a polynomial using Taylor’s formula (Figure 7.2)
where yk lies in the interval determined by xk and x. The next approximation to x* can be found from the equation
By this means, expressing xk + 1 from equation (7.16), we obtain the transformation xk →xk + 1, and this defines some iterative scheme. It is easy to show that the iterative sequence generated by (7.15) and (7.16) has the order p = s.
Next, we need to discuss how to choose an initial value x0 which initiates a convergent iterative process. Let x*∈I, with derivative ƒ(s)(x) continuous in I and f′(x)(s)(x)≠ 0 for all x∈ I. When conditions
are satisfied, and min(x*, xk) < xk + 1 < max(x*, xk), then the iterative sequence {xk} generated by (7.15) and (7.16) converges monotonically to x*.
Now, let us consider the particular methods which follow from general approach (7.15) and (7.16). When s = 2, equation (7.16) has the following form:
Solving this equation with respect to xk + 1, we obtain the following iterative scheme:
with g(x) = x − f(x)/f′(x). This is the well known Newton’s method and it has a simple geometrical interpretation. Function y(x) = f(xk) + f′(xk)(x − xk) is the tangent to the curve of f(x) at the point xk. Then approximation xk + l is the intersection point of the tangent with the x-axis. To choose an initial value x0 it is necessary to use condition (7.17) with s = 7.
When s = 3, equation (7.16) has the form
Solving this equation with respect to xk + 1, we obtain
To satisfy Theorem 7.1, we must add the last two terms of equation (7.21) when f′(x) > 0 and subtract them when f′(x) < 0. It should also be taken into account that the sum of the last two terms in expression (7.21) approaches zero near the root. This may result in the loss of accuracy. It is known that for quadratic equation ax2 + bx + c = 0, the following relation is valid:
After applying this conversion to (7.21), we finally arrive at the following iterative scheme:
An initial value x0 should be chosen from condition (7.18) with s = 8.
The polynomial Ps(xk + 1) may be reduced to a first-degree polynomial without changing the order of the iterative sequence generated. Two possibilities to modify equation (7.20) follow:
1) replace one of the (xk + 1 − xk) factors in (xk + 1 − xk)2 by − f(xk)/f′(xk). After solving the modified equation with respect to (xk + l − xk) we obtain the following iterative scheme:
2) replace (xk + rxk)2 by (f(xk)/f′(xk))7 Then after solving the modified equation with respect to (xk + 1 − xk) we get
These methods are more attractive in comparison to iterative scheme (7.22) because they have the same cubic convergence but computation of the square root is avoided.
The following function implements the fixed-point method to find the root of an equation f(x) = 0 such that the equation could be re written as x = g(x). It takes three input arguments; the first argument is a function handle. Here, it is the function g(x) which is related to function f(x), for which we want to find out the root. The second argument is the initial guess value of root. The last argument is the error tolerance of the search method as discussed previously. The code listing is as follows.
To find the root of an equation f(x) = cos(x) − x = 0. We will first re-write the equation as x = g(x) = cos(x). Then, we will implement the following function.
Then we will call the fixedpoint function as follows.
We don’t show all the results to save the space. It took 34 iterations to reach the approximate solution within desired error tolerance. We observed that even after trying with different initial root values closer to the root the performance of this method did not improve.
The following function implements the controlled fixed-point iterative method. It is a variation of the fixed-point method. The signature of the function remains almost the same except for the addition of the alpha control parameter. We do not need to transform the equation from f(x) = 0 to x = g(x) so the function handle in first argument should point to the m-script implementation of f(x) rather than g (x). The code is listed in the following.
We apply this function on the same problem, i.e.,
First, we should implement this function using m-script as given in the following listing.
Then, to apply the controlled fixed-point method on this function, we will make the following function call from the interpreter.
The result obtained is the same as in previous sections but it takes only 6 iterations to solve the same problem. Controller fixed-point method is an enormous improvement in terms of performance compared to the fixed-point method.
7.1.2 Multi-point iterative processes
To construct an iterative process with cubic convergence using one-point iteration, we need to employ the higher-order derivatives of f(x). This may sometimes result in much computational effort. Another way to achieve cubic convergence is to use a multi-point iterative scheme (see (7.5)). One of the procedures to construct such a scheme is based on a superposition. Let us calculate the next approximation xk + 1, in two stages (note that the first formula represents Newton’s method):
A combination of these two formulae results in the following iterative scheme:
The order of the iterative sequence is three, that is, ek + 1 = C(ek)3 In some cases, a multi-point iterative scheme is more efficient in comparison to one-point iteration. Only the function itself and its first derivative are employed and again we have rapid convergence. The construction procedure for iterative scheme (7.25) enables us to adopt the same condition for choosing the initial values as for Newton’s method.
By analogy with scheme (7.25), we can construct another iterative scheme:
and after the combination of these expressions we arrive at
This iterative scheme also produces the sequence with the order of convergence p = 3.
The following function implements Newton’s method of root approximation. In this function, the first argument points to the implementation of function f(x) whereas the second argument points to the implementation of first derivative of this function, f′(x). The third argument, x0, is the initial guess of the root and last argument, tol, is the error tolerance.
We use the same example as in the previous sections.
The implementation of this function is shown previously. The derivative of this function is as follows.
And the implementation of the derivative is as follows.
Then, to apply Newton’s method on this function, we will make the following function call from the interpreter.
Once again, the result obtained is the same as in previous methods and it takes 4 iterations to reach the solution. This is the best method so far. The only disadvantage of this method is that the user has to write the implementation of the derivative of the function as well. Readers could try to modify the above implementation and use the numerical approach to find out the derivative of the function. Although it will take longer to run the function, the user will not have to write the extra function implementation.
The multi-point method is implemented in the following. The function takes the same arguments as in Newton’s method.
We use the same example as in the previous sections.
To apply the multipoint method, we will make the following function call from the interpreter.
This method proves faster than Newton’s method. The result is the same as before and it takes even fewer iterations to reach the solution.
7.1.3 One-point iterative processes with memory
Despite the power of methods with superlinear convergence, their use of the derivatives f′(x) and f″(x) can be troublesome. It often requires much more effort to evaluate f′(x) and ƒ″(x) than f(x). In addition, many applications involve functions that do not have closed-form expressions for their derivatives.
In this section we consider some modifications to one-point iterations that avoid the exact evaluation of derivatives. The first derivative of f(x) at the point xk may be approximately evaluated in the following manner:
Substituting this expression in (7.19) we obtain
This is the secant method. Convergence of this iterative scheme is described by expression (7.8) with some constant C and p ≈ 1.62, which is slower than Newton’s method (p = 2). However, the secant method requires just one evaluation of f(xk) per iteration (we can use the value f(xk − 1) from the previous iteration). To start an iterative process we need to choose two initial values x0 and x1 To define these initial values, we can use the same condition we used for Newton’s method, except that the condition should be applied to x0 and x1:
The implementation of secant method in the following requires two guess values of the root, unlike the previous method.
We use the same example as in the previous sections.
The implementation of these functions is shown previously. To apply the secant method, we will make the following function call from the interpreter.
Secant method took only 4 iterations to find the root. Its performance is comparable to the multi-point method to solve this example.
7.2 Exercises
Find the root of equation f(x) = 0. If the equation has more than one root, then find the root that has the smallest magnitude. Calculate the root with prescribed tolerance using one of the iterative methods. To solve the problem find an interval that contains the root and initial guess that initiates the convergent iterative process. Suggested iterative methods are