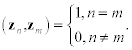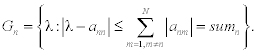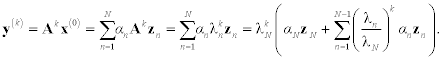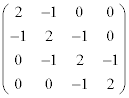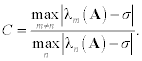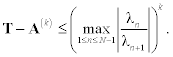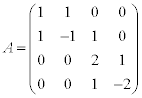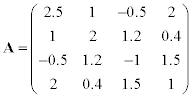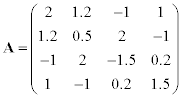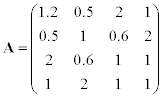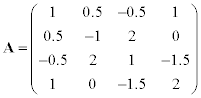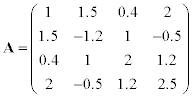9.1 Basic Facts concerning Eigenvalue Problems

Common linear algebra background is presented in section 8.1. Here we will consider some specific definitions related to the eigenvalue problem. In general, this problem is formulated as

where A and M are square N by N matrices and pair (λ_n, z_n) is an eigenvalue and associated eigenvector. In particular, this problem arises in the analysis of structural vibrations. We restrict our attention to a simpler problem (the standard eigenvalue problem):

(9.1)

The spectrum of a matrix A is the set of all N eigenvalues of A, and these eigenvalues are defined as zeros of the characteristic polynomial det(A−λI). Eigenvectors z_n (n = 1.…, N) form a system of orthonormal vectors:

In general, a square matrix A may have complex eigenvalues. Only matrices with a special property have exclusively real eigenvalues. These matrices are called Hermitian. Let “H” denote the successive application of two operations: complex conjugation and transposition, then a matrix A is Hermitian if A = A^H. In particular, a real symmetric matrix is a special case of a Hermitian matrix.

To be more specific, let us assume the following numbering of eigenvalues:

By this means, λ₁ is the eigenvalue with smallest magnitude and λ_N is the eigenvalue with largest magnitude.

The Rayleigh quotient for a matrix A is

for any x ≠ o. It plays an important role in the computation of eigenvalues because of its interesting properties, which are (1) λ₁ ≤ ρ(x) ≤ λ_N for all nonzero x∈R^N; (2) if x = z_n, then λ(x) = λ_n; and (3) on the basis of the previous property, the residual vector for the eigenvalue problem is introduced as

and the inequality r(x) ≤ Ax − αx holds for any λ. Therefore, if x is some approximation to z_n, then λ(x) is the best approximation to λ_n

9.2 Localization of Eigenvalues

Often one can obtain information about the location of eigenvalues in the complex plane without much computational effort. One of the easiest methods to use is based on the following theorem.

The set G_n defined in expression (9.2) is called the nth Gerschgorin disk of A. When all eigenvalues are real, then Gerschgorin disks are simply intervals. If n disks form the domain G isolated from other disks, then G contains exactly n eigenvalues of a matrix A. Hence the union of the Gerschgorin disks contains all eigenvalues of a matrix A. It is sometimes possible to get information about the disk that contains a single eigenvalue. This can be realized for matrices with specific properties, namely: if at some n for all k = 1, …, N(k ≠ n), the following inequalities are fulfilled

(9.3)

then the Gerschgorin disk |λ − a_nn| ≤ sum_n contains a single eigenvalue.

9.3 Power Method

This is a classical method used mainly in finding the dominant eigenvalue and eigenvector associated with this eigenvalue. It is not a general method, but it might be useful in a number of situations. For example, it is sometimes an appropriate method for large sparse matrices. In addition, the scheme of this method reveals some important aspects of the eigenvalue problem.

The power method is an iterative process to find eigenvectors of A. To begin with, let us perform some preliminary analysis. Take some initial vector x⁽⁰⁾ and suppose that all eigenvalues are different in magnitude. One can expand the vector x⁽⁰⁾ in terms of eigenvectors of A:

Multiplying the vector x⁽⁰⁾ repeatedly by the matrix A, we obtain

When k → ∞, y^(k): approaches a vector that is collinear with z_N. Thus, taking successive powers of A yields information about its eigenvalue λ_N. It is easy to find the dominant eigenvalue from this iteration. Taking into account the second property of the Rayleigh quotient, λ(y^(k)) approaches λ_N when k → ∞.

Incorporating these observations, one can suggest the following implementation of the power method:

If we need only the eigenvalue of a symmetric matrix A, then we can perform many fewer iterations. Let x^(k) be some approximation to z_n, so z_n = x^(k) + e^(k) and e^(k) = δ. The Rayleigh quotient for the vector x^(k) is

By this means, approximation x^(k) converges linearly to z_n, but λ(x^(k)) converges quadratically to λ_n.

The following implementation of power method is used to find the eigenvalue and eigenvector of the given square matrix. The function takes three input arguments; the square matrix, initial guess vector and error tolerance.

We want to find out an eigenvector and the corresponding eigenvalue for the given matrix in the following.

The pwr function will be called as follows.

Vector x is the eigenvector whereas value of l (3.6180) is an eigenvalue of the matrix A. It took 34 iterations to reach the solution with the desired accuracy of 10^− 5.

9.4 Inverse Iteration

The method of inverse iteration amounts to the power method applied to an appropriate inverse matrix. Let us consider briefly the main ideas behind the method. By multiplying by A^− 1, we can rewrite eigenvalue problem (9.1) in the following form:

This means that the eigenvector of a matrix A is the eigenvector of the matrix A^− 1 and λ_n(A^− 1) = 1/λ_n(A). Let us take some initial vector x⁽⁰⁾ and expand it in terms of eigenvectors of A:

Multiplying the vector x⁽⁰⁾ repeatedly by the matrix A^− 1, we obtain

When k → ∞, y^(k) approaches a vector that is collinear with z₁. Thus, taking successive powers of A^− 1 yields information about the eigenvalue of A, which is smallest in magnitude. In practice, we do not compute A^− 1 explicitly. Instead, it is much less expensive to solve Ay = x with respect to y, then compute y = A^− 1x. Incorporating these observations, we can suggest the following implementation of the method of inverse iteration:

The method of inverse iteration is more expensive than the power method, because we have to solve a system of linear equations at every step of the iterative process. However, the matrix A remains the same as we iterate, so we can initiate the algorithm by computing a factorization for A once (see 8.6), and then each iteration requires only forward and backward substitutions.

The following function implements the inverse iteration method. It uses the Jacobi function to solve the system of linear equations. The function signature is the same as in previous implementation of pwr method.

We apply this function on the same problem as in the last section.

This method finds a different eigenvector and eigenvalue compared to last method but it takes only 10 iterations. The actual cost of this method is hidden in solving the system of linear equations using the Jacobi method.

9.5 Iteration with a Shift of Origin

Often in practice it is more convenient to apply iterations not to a matrix A, but to the matrix B = A − σI (σ = const ≠ 0 is a shift of origin). This essentially does not change eigenvalue problem (9.1), because eigenvectors of A coincide with those of the matrix B and λ_n(A) = λ_n(B) + σ. In this case the power method will converge to some eigenvector z_n associated with the eigenvalue

and the asymptotic error constant is

The method of inverse iteration will converge to some eigenvector z_n associated with the eigenvalue

and the asymptotic error constant is

There are two situations in which we should use a shift of origin. In the first case, let |λ_N| and |λ_N − 1| be equal or very close for a given matrix A. By using the power method, we will fail to get convergence either to z_N or to z_N − 1 (or convergence will be very slow). When λ ≠ 0, all λ_n(B) are different in magnitude; therefore, we will get convergence.

For the second situation in which we should use a shift of origin, suppose we seek the eigenvalue of A lying closest to a prescribed point ß,

Then the method of inverse iteration with σ = ß converges to z_m.

In the following, we implement the power and inverse iteration methods with shift of origin. These implementations are based on the previous implementations. The function signatures remain the same except the addition of shift parameter, s.

We apply the above functions to find the eigenvector and eigenvalue for the following matrix.

9.6 The QR Method

The most widely used method for computing eigenvalues is the QR method. This method has several valuable features: (1) it finds all eigenvalues of a matrix; (2) its behavior in the presence of equal-magnitude eigenvalues allows us to get some useful information about the spectrum of a matrix; and (3) it is simplified when the matrix under consideration is symmetric.

The idea of the QR method is simple. Given A, we factorize A = A⁽⁰⁾ = QR, where Q is an orthogonal matrix and R is an upper triangular matrix. We then compute a new matrix A⁽¹⁾ = RQ. The procedure continues by induction: given A^(k) = Q^(k)R^(k), we compute A^(k + 1) = R^(k)Q^(k). The procedure is straightforward, but it produces a very interesting result: if all |λ_n| are different, then

where

(9.4)

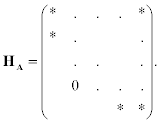
By this means, we can compute all eigenvalues in one iterative process. However, the QR method as outlined requires too much arithmetic to be practical. For a general matrix A, each QR factorization requires O(N³) operations. To overcome this obstacle, one can perform an initial transformation on A that reduces it to a form for which succeeding QR factorizations are much cheaper. In particular, we begin the QR method by converting A to H_A, which is in Hessenberg form:

After this reduction, it is possible to compute the QR factorization of the initial matrix A⁽⁰⁾ = H_A in O(N²) operations. More importantly, each matrix A^(k) remains in Hessenberg form. For symmetric matrices, the Hessenberg form is tridiagonal, so much less arithmetic and storage are required. To evaluate convergence, we can monitor the decay of the subdiagonal entries a_n + l.n in the matrices A^(k); alternatively we can also monitor the decay of

The following algorithm summarizes all considerations outlined:

If

then the entries a_nn^(k) are approximate eigenvalues of A and |λ_n(A) − a_nn^(k)| ≤ ε_p.

The qr function to find the QR factors of a matrix is a built-in function so there is no need to implement again. In the following function, we use this method to find out all eigenvalues of a given matrix.

We want to find out all the eigenvalues of the following matrix.

The answer is incorrect since it takes zero iteration to reach the solution which is impossible. Now, we will shift the origin of given matrix A by s = 1 then apply the same function.

The shift matrix converged to the solution in 7 iterations. In order to get the eigenvalues of original matrix A, we subtracted the shift value s = 1 from vector l.

9.7 Exercises

Given symmetrical matrix A, solve one of the following problems:

Methodical comments: to solve systems of linear equations in the method of inverse iteration use the LU-factorization; to transform matrix into Hessenberg form in QR method use the function hess (A).

Set of symmetrical matrices: