26.1 INTRODUCTION

Large amounts of computer time and storage requirements can be used when performing least squares adjustments. This is due to the fact that as the problems become more complex, the matrices become larger, and the storage requirements and time consumed in doing numerical operations grow rapidly. As an example, in analyzing the storage requirements of a 25-station horizontal least squares adjustment that has 50 distance and 50 angle observations, the coefficient matrix would have dimensions of 100 rows and 50 columns. If this adjustment were done in double precision,¹ it would require 40,000 bytes of storage for the coefficient matrix alone. The weight matrix would require an additional 80,000 bytes of storage. Also, at least two additional similarly sized intermediate matrices² must be formed in computing the solution. From this example, it is easy to see that large quantities of computer time and computer memory can be required in least squares adjustments. Thus, when writing least squares software, it is desirable to take advantage of some storage and computing optimization techniques. In this chapter, some of these techniques are described.

26.2 STORAGE OPTIMIZATION

Many matrices used in a surveying adjustment are large but sparse. Using the example above, a single row of the coefficient matrix for a distance observation would require a 50-element row for its four nonzero elements. In fact, the entire coefficient matrix is sparsely populated by nonzero values. Similarly, the normal matrix is always symmetric, and thus nearly half its storage is used by duplicate entries. It is relatively easy to take advantage of these conditions to reduce the storage requirements.

For the normal matrix, only its upper- or lower-triangular portion of the matrix need be saved. In this storage scheme, the two-dimensional matrix is saved as a vector. An example of a 4 × 4 normal matrix is shown in Figure 26.1. Its upper- and lower-triangular components are shown separated and their elements numbered for reference. The vector on the right of Figure 26.1 shows the storage scheme. This scheme eliminates the need to save the duplicate entries of the normal matrix, but requires some form of relational mapping between the original matrix indices of row i and column j and the vector's index of row i. For the upper triangular portion of the matrix, it can be shown that the vector index for any (i, j) element is computed as

(26.1)

Using the function given in Equation (26.1), the vector index for element (2, 3) of the normal matrix would be computed as

An equivalent mapping formula for the lower-triangular portion of the matrix is given as

(26.2)

Equation (26.1) or (26.2) can be used to compute the storage location for each element in the upper or lower part of the normal matrix, respectively. Of course, it requires additional computational time to map the location of each element every time it is used. One method of minimizing computing time is to utilize a mapping table. The mapping table is a vector of integers that identifies the storage location for only the initial element of a row or column. To reduce total computational time, the indices are stored as one number less than their actual value. For the example matrix stored in Figure 26.1, it would have a relational mapping table of

Although the storage location of the first element is 1, it can be seen above that it is identified as 0. Similarly, every other mapping index is one number less than its actual location in the vector, as shown in Figure 26.1. The mapping vector is found using the pseudocode shown in Table 26.1.

By using this type of mapping table, the storage location for the first element of any upper-triangular column is computed as

(26.3)

Using the mapping table, the storage location for the (2, 3) element is

The equivalent formula for the lower triangular portion is

(26.4)

Obviously, this method of indexing an element's position requires additional storage in a mapping table, but the additional storage is offset by the decreased computational time that is created by multiplication operations in Equations (26.1) and (26.2). Although every compiler and machine are different, a set of times to compare indexing methods are shown in Table 26.2. The best times were achieved by minimizing both the number of operations and calls to the mapping function. Thus, in method C, the mapping table was created to be a global variable in the program and the table was accessed directly as needed. For comparison, the time to access the matrix elements directly using the loop shown in method D was 1.204 seconds. Thus, method C uses only slightly more time than method D but helps avoid the additional memory that is required by the full matrix required for method D. Meanwhile, method A is slower than method C by a factor of 3. Since the matrix elements must be accessed repeatedly during a least squares solution, this difference can be a significant addition to the total solution time.

Method A: Using function A
    i from 1 to 1000
        j from i to 1000
            k = Index( i,j ) 

Method B: Using function B
    i from 1 to 1000
        j from i to 1000
            k = Index( i,j ) 

Method C: Direct access to mapping table
    i from 1 to 1000
        j from i to 1000
            k = VI(j) + I

Method D: Direct matrix element access.
    i from 1 to 1000
        j from 1 to 1000
            k = A[i,j]

The additional overhead cost of having the mapping table is minimized by declaring it as an integer array so that each element requires only two bytes of storage. In the earlier example of 25 stations, this results in 100 bytes of additional storage for the mapping table. Speed versus storage is a decision that every programmer will continually face.

26.3 DIRECT FORMATION OF THE NORMAL EQUATIONS

The basic weighted observation equation form is WAX = WL + WV. The least squares solution for this equation is X = (A^TWA)⁻¹(A^TWL) = N⁻¹C, where A^TWA is the normal equations matrix N, and A^TWL is the constants matrix C. If the weight matrix is diagonal, formation of the A, W, L, and A^TW matrices is unnecessary when building the normal equations and the storage requirements for them can be eliminated. This is accomplished by forming the normal matrix directly from the observations. The tabular method in Section 11.8 showed the feasibility of this method. Notice in Table 11.2 that the contribution of each observation to the normal matrix is computed individually and, subsequently, added. This shows that there is no need to form the coefficient, constants, weight, or any intermediate matrices when deriving the normal matrix. Conceptually, this is developed as follows:

• Step 1: Zero the normal and constants matrix.
• Step 2: Zero a single row of the coefficient matrix.
• Step 3: Based on the values of a single row of the coefficient matrix, add the proper value to the appropriate normal and constant elements.
• Step 4: Repeat steps 3 and 4 for all observations.

This procedure works in all situations that involve a diagonal weight matrix. Procedural modifications can be developed for weight matrices with limited correlation between the observations. Computer algorithms in BASIC, FORTRAN, C, and Pascal for this method are shown in Table 26.3.

For i = 1 to unknown
  ix = VI(i): ixi = ix + i
  N(ixi) = N(ixi) + A(i)^2 * W(i)
  C(i) = C(i) + A(i)*W(i)*L(i)
  For j = i+1 to unknown
    N(ix+j) = N(ix+j) + A(i)*W(i)*A(j)
  Next j
Next I

Do 100 i = 1, unknown
   ix = VI(i)
   ixi = ix + i
   N(ixi) = N(ixi) + A(i)**2 * W(i)
   C(i) = C(i) + A(i)*W(i)*L(i)
   Do 100 j = i+1, unknown
      N(ix+j) = N(ix+j) + A(i)*W(i)*A(j)
100  Continue

for ( i=1; i<=unknown; i++) {
  ix = VI[i]; ixi = ix + i;
  n[ixi] = n[ixi] + a[i]*a[i] * w[i];
  c[i] = c[i] + a[i]*w[i]*l[i];
  for ( j=i+1; j<=unknown; j++)
    n[ix+j] = n[ix+j] + a[i]*w[i]*a[j];
}// for i

For i := 1 to unknown do begin
  ix := VI[i]; ixi := ix + i;
  N[ixi] := N[ixi] + Sqr(A[i]) * W[i];
  C[i] := C[i] + A[i]*W[i]*L[i];
  For j := i+1 to unknown do
    N[ix+j] := N[ix+j] + A[i]*W[i]*A[j]
End; { for i }

26.4 CHOLESKY DECOMPOSITION

Having formed only a triangular portion of the normal matrix, a Cholesky decomposition can be used to greatly reduce the time needed to find the solution. This procedure takes advantage of the fact that the normal matrix is always a positive-definite matrix.³ Due to this property, it can be expressed as the product of a lower-triangular matrix and its transpose; that is,

where L is a lower triangular matrix of the form

When the normal matrix is stored as a lower-triangular matrix, it can be factored using the following procedure:

for i = 1, 2,…, number of unknowns compute

(26.5)

for j = i + 1, i + 2,…, number of unknowns compute

The procedures above are shown in code-form in Table 26.4.

FOR i = 1 TO unknown
  ix = VI(i): ixi = ix + i: s = 0#
   FOR k = 1 TO i - 1
       s = s + N(ix + k) ^ 2: NEXT k
   N(ixi) = SQR(N(ixi) - s)
   FOR j = i + 1 TO unknown
     s = 0#: jx = VI(j)
     FOR k = 1 TO i - 1
 s = s + N(jx + k) * N(ix + k): NEXT k
     N(jx + i) = (N(jx + i) - s) / N(ixi)
   NEXT j
 NEXT i

   Do 30 i = 1,Unknown
    ix = VI(i)
    i1 = i - 1
     S = 0.0
        Do 10 k=1, i1
   10   s = s + N( ix+k )**2
     N(ix+i) = Sqrt( N(ix+i)-s )
      Do 30 j = i+1, Unknown
       s = 0.0
       Do 20 k = 1, i1
   20     s = s + N( VI[j]+k ) * N( ix+k )
       N(VI[j]+i) =
       
 (N(VI[j]+i) -s) / N(ix+i)
   30  Continue

for ( i=1; i<=unknown; i++ ) {
 ix = VI[i]; ixi = ix+i; s = 0.0;
 for ( k=1; k<i; k++ )
    s = s + n[ix+k]*n[ix+k];
 n[ixi] = sqrt( n[ixi] - s );
 for ( j=i+1; j<=unknown; j++ ) {
    s = 0; jx = VI[j];
    for ( k=1; k<i; k++)
      s = s + n[jx+k] * n[ix+k];
    n[jx+i] = ( n[jx+i] - s ) / n[ixi];
 } // for j
} // for i

  For i := 1 to unknown do Begin
    ix := VI[i]; ixi := ix+i;   S := 0;
    For k := 1 to Pred( i ) do 
        S := S + Sqr( N[ix+k] );
    N[ixi] := Sqrt( N[ixi] -S );
    For j := Succ(i) to unknown do Begin
      S := 0; jx := VI[j];
      For k := 1 to Pred(i) do 
          S := S + N[jx+k]*N[ix+k];
      N[jx+i] := ( N[jx+i] - S ) / N[ixi]
    End; { for j}
  End; { for i }

26.5 FORWARD AND BACK SOLUTIONS

Being able to factor the normal matrix into triangular matrices has the advantage that the matrix solution can be obtained without the use of an inverse. The equivalent triangular matrices representing the normal equations are

(26.6)

Equation (26.6) can be rewritten as LY = C, where L^TX = Y. From this, the solution for Y can be found by taking advantage of the triangular form of L. This is known as a forward substitution. Steps involved in forward substitution are

• Step 1: Solve for y₁ as .
• Step 2: Substitute this value into row 2, and compute y₂ as .
• Step 3: Repeat this procedure until all values for y are found using the algorithm

Having determined Y, the solution for the matrix system L^TX = Y is computed in a manner similar to that above. However, this time the solution starts at the lower-right corner and proceeds up the matrix L^T. This is called a backward substitution, which is done with the following steps:

• Step 1: Compute x_n as .
• Step 2: Solve for x_n−1 as .
• Step 3: Repeat this procedure until all unknowns are computed using the algorithm

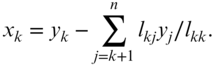
In this process, once the original values in the constant matrix are accessed and changed, they are not needed again, and the original C matrix can be overwritten with Y and X matrices so that the entire process requires no additional storage. In fact, this method of solution also requires fewer operations than solving X = (A^TWA)⁻¹A^TWL directly. Table 26.5 lists the computer codes for these algorithms.

Rem Forward Substitution
For i = 1 to Unknown
  ix = VI(i)
  C(i) = C(i) / N(ix+i)
  For j = i+1 to Unknown
    C(j) = C(j) - N(ix+j) * C(i)
  Next j
Next i
Rem Backward Substitution
For i = Unknown to 1 Step -1
  ix = VI(i)
  For j = Unknown To i+1 Step -1
    C(i) = N(ix+j) * C(j)
  Next j
  C(i) = C(i) / N(ix+i)
Next i

C Forward Substitution
  Do 100 i = 1,Unknown
    ix = VI(i)
    C(i) = C(i) / N(ix+i)
    Do 100 j = i+1, Unknown
      C(j) = C(j) - N(ix+j) * C(i)
100 Continue

C Backward Substitution
   Do 110 i = Unknown, 1,-1
     ix = VI(i)
     Do 120 j = Unknown, i+1, -1
120     C(i) = C(i) - N(Ix+j) * C(j)
     C(i) = C(i) / N(Ix+i)
110 Continue

//Forward Substitution
for (i=1; i<=unknown; i++){
  ix = VI[i];
c[i] = c[i]/n[ix+i];
for (j=i+1; j<=unknown; j++){
   c[j] = c[j] - n[ix+j]*c[i];
} //for j
} //for i
//backward substitution
for (i=unknown; i>=1; i--){
 ix = VI[i];
 for (j=unknown; j>=i+1; j--){
   c[i] = c[i] - n[ix+j] * c[j];
 } //for j
c[i] = c[i]/n[ix+i];
} // for i

{Forward Substitution}
For i := 1 to Unknown Do Begin
  ix := VI[i];
  C[i] := C[i] / N[ix+i];
  For j := i+1 to Unknown Do
    C[j] := C[j] - N[ix+j] * C[i];
End; { for i }

{Backward Substitution}
For i := Unknown DownTo 1 do Begin
  ix := VI[i];
  For j := Unknown DownTo i+1 Do 
     C[i] := C[i] - N[Ix+j] * C[j];
  C[i] := C[i] / N[Ix+i];
End; { for i }

26.6 USING THE CHOLESKY FACTOR TO FIND THE INVERSE OF THE NORMAL MATRIX

If necessary, the original normal matrix inverse can be found with the Cholesky factor. To derive this matrix, the inverse of the Cholesky factor is computed. The normal matrix inverse is the product of this inverse times its transpose. The Cholesky factor inverse is determined using the algorithm in Table 26.6. Code for this algorithm is shown in Table 26.7.

for i going from the number of unknowns down to 1 
   for k going from number of unknowns down to i + 1
           for j going from i+1 to k, sum the product N(i, j) * N(j, k)
           N(i, k) = -S / N(i, i)
   N(i, i) = 1/N(i, i)

{Inverse}
For i = Unknown To 1 Step -1
   ix = VI(i): ixi = ix + i
   For k = Unknown To i+1 Step -1
      S = 0!
      For j = i+1 To k
         S = S + N(ix+j) * N(VI(j)+k)
      Next j
      N(ix+k) = -S / N(ixi)
   Next k
   N(ixi) = 1.0 / N(ixi)
Next i
 
{Inverse * Transpose of Inverse}
For j = 1 to Unknown 
     ixj = VI(j)
    For k = j to Unknown
       S = 0!
      For i = k to Unknown 
        S = S + N(VI(k)+i) * N(ixj+i)
      Next i
      N(ixj+k) = S
    Next k
Next j

C Inverse
 Do 10 i = Unknown, 1,-1
  ix = VI(i)
  ixi = ix + i
  Do 11 k = Unknown, i+1,-1
   S = 0.0
   Do 12 j = i+1,k
12   S = S + N(ix+j) * N(VI(j)+k)
   N(ix+k) = -S / N(ixi)
11  Continue
  N(ixi) = 1.0 / N(ixi)
10 Continue
 
C  Inverse * Transpose of Inverse}
 Do 20 j = 1, Unknown
  ixj = VI(j)
  Do 21 k = j, Unknown
   S = 0.0
   Do 22  i = k,Unknown
22    S = S + N(VI(k)+i) * N(ixj+i)
   N(ixj+k) = S
21  Continue
20 Continue

{Inverse}
for ( i=unknown; i>=1; i--) {
   ix = VI[i]; ixi = ix + i;
   for( k=unknown; k>=i+1; k--) {
      S = 0.0;
      for ( j=i+1; j<=k; j++) 
         S = S + N[ix+j] * N[VI[j]+k];
      N[ix+k] = -S / N[ixi];
   } // for k 
   N[ixi] = 1.0 / N[ixi];
} // for i

{inverse * transpose of inverse}
for (j=1; j<=unknown; j++) {
     ixj = VI[j];
    for (k=j; k<=unknown; k++) {
       S = 0.0;
      For (i=k; i<=unknown; i++) 
        S = S + N[VI[k]+i] * N[ixj+i];
      N[ixj+k] = S
    } // for k 
} //for j

{Inverse}
For i := Unknown DownTo 1 do Begin
   ix := VI[i]; ixi := ix + i;
   For k := Unknown DownTo i+1 Do Begin
      S := 0.0;
      For j := i+1 To k Do 
         S := S + N[ix+j] * N[VI[j]+k];
      N[ix+k] := -S / N[ixi];
   End; { For k }
   N[ixi] := 1.0 / N[ixi];
End; { For i }
{Inverse * Transpose of Inverse}

For j := 1 to Unknown Do Begin
     ixj := VI[j];
    For k := j to Unknown Do Begin
       S := 0.0;
      For i := k to Unknown Do
        S := S + N[VI[k]+i] * N[ixj+i];
      N[ixj+k] := S
    End; { For k }
End; { For j }

26.7 SPARENESS AND OPTIMIZATION OF THE NORMAL MATRIX

In the least squares adjustment of most surveying and photogrammetry problems, it is known that certain locations in the normal matrix will contain zeros. The network shown in Figure 26.2 can be used to demonstrate this fact. In that figure, assume that distances and angles were observed for every line and arc, respectively. The following observations are made about the network's connectivity. Station 1 is connected to stations 2 and 8 by distance observations and is also connected to stations 2, 3, and 8 by angles. Notice that its connection to station 3 is due to angles turned at both 2 and 8. Since these angles directly connect stations 1 and 2, it follows that if the coordinates of 3 change, so will the coordinates of 1, and thus with respect to station 1, the normal matrix can be expected to have nonzero elements corresponding to the stations 1, 2, 3, and 8. Conversely, the positions corresponding to stations 4, 5, 6, and 7 will have zeros.

Using this analysis with station 3, because it is connected to stations 1, 2, 4, 7, and 8 by angles, zero elements can be expected in the normal matrix corresponding to stations 5 and 6. This analysis can be made for each station. The resulting symbolic normal matrix representation is shown in Figure 26.3.

A process known as reordering the unknowns can minimize both storage and computational time. Examine the matrix shown in Figure 26.4 that results from placing the unknowns of Figure 26.3 in the order of 6, 5, 4, 7, 3, 1, 2, and 8. This new matrix has its nonzero elements immediately adjacent to the diagonal elements, and thus the known zero elements are grouped together and appear in the leftmost columns of their respective matrix rows. By modifying the mapping table, storing the known zero elements of the original matrix in Figure 26.3 can be avoided, as is shown in the column matrix of Figure 26.4.

This storage scheme requires a mapping table that provides the storage location for the first nonzero element of each row. Since the diagonal elements are always nonzero, they can be stored in a separate column matrix without loss of efficiency. Ignoring the fact that each station has two unknowns, the mapping of the first element for each row is 1, 1, 2, 4, 7, 9, 10, 12, and 17. This mapping scheme enables finding the starting position for each row and allows for the determination of the off-diagonal length of the row. That is, row 1 starts at position 1 of the column matrix, but has a length of zero (1 − 1), indicating that there are no off-diagonal elements in this row. Row 2 starts at position 1 of the column matrix and has a length of (2 − 1) = 1. Row 5 starts at 7 and has a length of (9 − 7) = 2. By optimizing for matrix sparseness and symmetry, only 24, (16 + 8), elements of the original 64-element matrix need be stored.

This storage savings, when exploited, can also result in a savings of computational time. To understand this, first examine how the Cholesky factorization procedure processes the normal matrix. For a lower triangular matrix factorization process, Figure 26.5 shows the manner in which elements are accessed. Notice when a particular column is modified, the elements to the left of this column are used. Also notice that no rows above the corresponding diagonal element are used.

To see how the reorganized sparse matrix can be exploited in the factorization process, the processing steps must be understood. In Figure 26.4 the first two elements of row 5 are known zeros, and each summation loop in the factorization process should start with the third column. If the zeros in the off-diagonals are rearranged such that they occur in the leftmost columns of the rows, it is possible to avoid that portion of the operations for the rows. Notice how the rows near the lower portion of the matrix are optimized to minimize the computational effort. A savings of eight multiplications is obtained for computations of column 5. In a large system, the cost savings of this optimization technique can be enormous. A complete discussion of these techniques is presented by George and Lui (1981). A comparison of the operations performed when computing column 5 in Figure 26.4 using a Cholesky decomposition of both a full and optimized solution routine are shown in Table 26.8. Note that computations for rows 6 and 7 do not exist since these rows had known zeros in the columns before column 5 after the reordering process. If only the more time-consuming multiplication and division operations are counted, the optimized solution requires 5 operations as compared to 19 in the nonoptimized (full) solution.

	Full Operations	Optimized Operations
1
2	n55 = square root of ( n55 − s )	n55 = square root of ( n55 − s )
3	j = 6 (a) (b) n65 = (n65 − s)/n55 j = 7 (a) (b) n75 = (n75 − s)/n55 j = 8 (a) (b) n85 = (n85 − s)/n55	j = 6 no operations necessary j = 7 no operations necessary j = 8

Several methods have been developed to optimize the ordering of the unknowns. Two of the more well-known reordering schemes are the reverse Cuthill–Mckee and the Snay's banker's algorithm. Both of these algorithms reorder stations based on their connectivity. The example of Figure 26.2 will be used to demonstrate the banker's algorithm. In this example, a connectivity matrix is first developed. This is simply a list of stations that are connected to a given station by either an angle or distance observations. For instance, station 1 is connected to stations 2 and 8 by distances, and additionally to station 3 by angles. The complete connectivity matrix of Figure 26.2 is listed in the first two columns of Table 26.9. In addition to the connectivity, the algorithms also need to know the number of connected points for each station. This is known as the station's degree.

To start the reordering, select the station with the lowest degree. In this example, that could be either station 1, 2, 5, or 6. For demonstration purposes, begin with station 6. This station is now removed from each station's connectivity matrix, and thus stations 4, 5, and 7 have their degrees reduced by one. This is shown in column 6. Now select the next station with the smallest degree. Since station 5 had its degree reduced to 2 when station 6 was selected, it now has the smallest degree. This process is continued, that is, the next station with the smallest degree is selected and is removed from the connectivity of the remaining stations. If two or more stations have the smallest degree, the most recently changed station with the smallest degree is chosen. In this example, this happened after choosing station 5. Station 4 was selected over stations 1 and 2 simply because it just had its degree reduced. Although station 7 qualified equally to station 4, station 4 was higher on the list and was selected for that reason alone. This happened again after selecting station 7. Station 3 was the next choice since it was the first station reduced to a degree of 3. Note that the final selection of station 8 was omitted from the list.

A similar optimized reordering can be found by starting with station 1, 2, or 5. This is left as an exercise. For a computer algorithm of this reordering the reader should refer to the NOAA Technical Memorandum NGS 4 by Richard Snay; the computer algorithm for the reverse Cuthill–McKee is given in the book by George and Lui (see the Bibliography).

PROBLEMS

1. 26.1 Explain why computer optimization techniques are necessary for doing large least squares adjustments.
2. 26.2 When using double precision, how much computer memory is required in forming the J, W, K, J^T, J^TW, J^TWK, and J^TWJ matrices for a 20-station adjustment having 50 total observations?
3. 26.3 If the normal matrix of Problem 26.2 were stored in lower triangular form and computed directly from the observations, how much storage would be required?
4. 26.4 Discuss how computational savings are created when solving the normal equations by Cholesky factorization and substitution.
5. 26.5 Write a comparison of an operations table similar to that in Table 26.8 for column 3 of the matrix shown in Figure 26.4.
6. 26.6 Same question as Problem 26.5 except with column 6.
7. 26.7 Using the station reordering algorithm presented in Section 26.7, develop a connectivity matrix and reorder the stations when starting with station 1. Draw the normal matrix of the newly reordered station's which is similar to the sketch shown in Figure 26.4.
8. 26.8 Same as Problem 26.7 except start the reordering with station 2.
9. 26.9 Same as Problem 26.7 except start the reordering with station 5.

PROGRAMMING PROBLEMS

1. 26.10 Develop a least squares program similar to those developed in Chapter 16 that builds the normal equations directly from the observations and uses a Cholesky factorization procedure to find the solution.
2. 26.11 Develop a Mathcad® worksheet that solves Problem 26.10.