APPENDIX F
MAP PROJECTION COORDINATE SYSTEMS
F.1 INTRODUCTION
Most local surveyors are well-served by using map projections such as the State Plane Coordinate System. These two-dimensional grid systems allow surveyors to perform accurate computations over large regions of land using plane surveying computations. They are the basis for the adjustments discussed in Chapters 14 through 16.
Map projections provide a 1-to-1 mathematical relationship with points on the ellipsoid and those on the mapping surface. There are an infinite number of map projections. Most map projections are defined by a series of mathematical transformations used to convert a point's geodetic coordinates of latitude, φ, and longitude, λ, to NE (y, x) grid coordinates. Some map projections preserve the shape of objects (conformal), others areas, directions, or distances of lines. However since the Earth is ellipsoidal in shape and a mapping surface is a plane, all map projections introduce some form of distortion to observations. For example, distances and areas are distorted in a conformal map projection.
Often, to reduce the size of these distortions, the developable surface is made secant to the ellipsoid and the width of the mapping zone is limited in distance. For instance, when the National Geodetic Survey originally designed the state plane coordinate system during the 1930s, the zone widths were limited to 158 mi so that precision between the ellipsoid distance and the grid distance were no worse than 1:10,000. Since most surveys, at that time, were only accurate to a precision of 1:5000, this was an acceptable limit. However, with today's modern instruments, proper reduction of observations must be performed if the accuracy of the surveys is to be preserved in a map projection system.
All map projections are based on a selected ellipsoid such as the Geodetic Reference System of 1980 (GRS 80) and defining zone parameters. Typically, the zone parameters define the grid origin (φ0, λ0), secant lines of the projection, also known as standard parallels, or scale factor, k0, at the central meridian, λ0, and the offset distances (E0, Nb) from the grid origin. Once defined, each map projection has a series of zone constants that are computed using the defining zone parameters. These zone constants are computed only once for each projection. Following this, the direct and inverse problems can be performed for any point in the system. The direct problem takes the geodetic coordinates of a point and transforms them into grid coordinates, and the inverse problem takes the grid coordinates of a point and transforms them into geodetic coordinates.
The two primary map projection systems used in the United States are the Lambert Conformal Conic for states having long east–west extents and the Transverse Mercator for states having long north–south extents. Both map projections are conformal. That is, they preserve angles in infinitesimally small regions about a point. This property is advantageous to surveyors since angles are minimally distorted when using a conformal projection. On the other hand, as shown in Figure F.1, observed horizontal distances must be reduced to the mapping surface to eliminate the distortions in the projection. However, if these reductions are performed properly, the resulting plane computations are as accurate as geodetic computations such as those presented in Chapter 23. This Appendix will look at the mathematics of the Lambert Conformal Conic, Transverse Mercator, and oblique stereographic map projections and demonstrate proper methods in reducing observations before an adjustment.
FIGURE F.1 Reduction of a distance to a mapping surface.
F.2 MATHEMATICS OF THE LAMBERT CONFORMAL CONIC MAP PROJECTION
The Lambert Conformal Conic map projection was first introduced by Johann Lambert in 1772. As its name implies, this map projection uses a cone as its developable surface. The projection is conformal so that angles are preserved in a limited region about a point, but distances are distorted. A Lambert Conformal Conic map projection is defined by two ellipsoidal parameters,1 grid origin (φ0, λ0), latitude of the north standard parallel, φN, and south standard parallel,2 φS, false easting, E0, and false northing, Nb.
F.2.1 Zone Constants
Three functions are used repeatedly in the computations of the Lambert Conformal Conic map projection:
Using Equations (F.1) through (F.3), the remaining zone constants are defined as
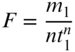
F.2.2 Direct Problem
The direct problem takes the geodetic coordinates of latitude, 
, and longitude, λ, of a point and transforms them into xy grid coordinates. Often, the y coordinate is called the point's northing, N, and the x coordinate its easting, E. Thus, given the geodetic coordinates of a point, the northing (y), easting (x), scale factor, k, and convergence angle, γ, of the point are computed as
F.2.3 Inverse Problem
The inverse problem takes a point's northing and easting coordinates and computes its latitude, longitude, scale factor, and convergence angle. For the Lambert Conformal Conic map projection, the equations for the inverse problem are
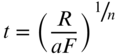
Repeat Equation (F.27) using χ for 
in the first iteration. Iterate until the change is φ is insignificant; that is, the change should be less than 0.000005″.
where m and t are defined in Equations (F.14) and (F.15) using 
from Equation (F.27).
The Mathcad® worksheet Lambert.xmcd on the companion website demonstrates both the direct and inverse problems using the Lambert Conformal Conic map projection.
F.3 MATHEMATICS FROM THE TRANSVERSE MERCATOR
The Transverse Mercator map projection uses a cylinder as its developable surface. It preserves scale in a north–south direction, and thus is good for regions with long north–south extent. This projection was originally proposed by Johann Lambert, but the mathematics for the ellipsoid were not solved until the early twentieth century. In many countries, this projection is also known as the Gauss-Krüger map projection. The most well-known Transverse Mercator map projection is the Universal Transverse Mercator (UTM), which was developed by the National Geospatial-Information Agency to provide a worldwide mapping system from 80° S latitude to 80° north latitude. This map projection is defined by two ellipsoidal parameters,3 grid origin (
, λ0), scale factor, k0, at the central meridian, λ0, false easting, E0, and false northing, Nb.
There are 60 zones in the Universal Transverse Mercator map projection, with each being nominally 6° wide. Each zone overlaps its neighboring zones by 30′. The central meridian, λ0, for each zone is assigned a false easting, E0, of 500,000 m. The false northing, Nb, in the northern hemisphere of 0.000 m and is 10,000,000.000 m in the southern hemisphere. The scale factor at the central meridian, k0, is 0.9996, which yields a distance precision of 1:2500. The central meridians (λ0) for each zone start at 177° W longitude and with a few exceptions proceeds easterly by 6° for each subsequent zone. The grid origins are at 0° and λ0.
F.3.1 Zone Constants
The Transverse Mercator map projection uses the following defining functions
where e is the first eccentricity of the ellipse as defined in Equation (17.5) and e′ is defined as
F.3.2 Direct Problem
The equations in the Transverse Mercator for the direct problem are
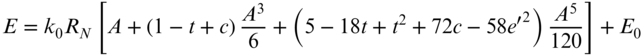
where RN is the radius in the prime vertical as defined by N in Equation (17.6).
F.3.3 Inverse Problem
The equations in the Transverse Mercator for the inverse problem are
The so-called foot-point latitude is
Using the foot-point latitude and functions defined in Section F.3.1 and Equation (17.5):
Note that Equations (F.41) and (F.42) can be used to compute the convergence angle γ and scale factor k for the point. The Mathcad® worksheet TM.xmcd on the companion website demonstrates both the direct and inverse problems using the Lambert Conformal Conic map projection.
F.4 STEREOGRAPHIC MAP PROJECTION
As discussed in Section 24.5, the oblique stereographic map projection is often used as a temporal coordinate system when transforming GNSS coordinates into some local or arbitrary coordinate system. The stereographic map projection uses a plane as its developable surface. Its definition only requires the geodetic coordinates of the origin and the scale factor at the origin. As discussed in Section 24.5, a scale factor is often chosen so that the map projection plane is at the elevation of the project, thus placing grid distances at grade and eliminating the need to perform reduction of observations as discussed in Section F.5.
As previously stated, an individual map projection coordinate system is defined by its grid origin (φ0, λ0) and scale factor k0. It uses the common functions:
where e is the eccentricity of the defining ellipsoid as given in Equation (17.5). Using these equations, the zone constants for the projection are
Using the geodetic coordinates of (
, λ) for a point and the semimajor axis a for the ellipsoid, the equations for the direct problem are
The inverse problem converts the map projection coordinates of (N, E) back to geodetic latitude and longitude. This conversion is not necessary for use in Section 24.5 since the goal of the problem is to convert the geodetic coordinates into an arbitrary or local coordinate system. However, by inversing the process, the geodetic coordinates of any point in the local coordinate system can be found. The equations used in the inverse problem for the oblique stereographic map projection are
Using φ equal to χ in the first iteration, Equation (F.71) is iterated until the change in φ becomes negligible. The scale factor is computed using Equation (F.66). Computations for the oblique stereographic map projection are demonstrated in the Mathcad® worksheets C24-2.xmcd and ostereo.xmcd on the companion website.
F.5 REDUCTION OF OBSERVATIONS
Most often, the grid coordinates of a point are known prior to the survey and all that is needed is to reduce the observations to the mapping surface. The basic principle to bear in mind is that grid computations should only be performed with grid observations. Since the map projections discussed previously are conformal, observed distances must be reduced to the mapping surface to preserve then accuracy of the survey. Additionally, geodetic and astronomical directions must be converted to their grid equivalents.
As will be discussed in this section, conformality implies that the angles will be only slightly distorted. As will be shown, the so-called arc-to-chord correction is applied when the sight distances are long. For example in the State Plane Coordinate System, the NGS recommended this correction for angles having sight distances that are greater than 8 km. In this section, the proper reduction of distance, direction, and angle observations will be discussed.
F.5.1 Reduction of Distances
As shown in Figure F.1, an observed horizontal distance must be reduced to the mapping surface. This reduction usually involves using the so-called combined factor. The combined factor is the product of the elevation factor that reduces the observed distance to the ellipsoid and a scale factor (k), which reduces the ellipsoidal distance to the mapping surface.
There are several procedures for reducing an observed distance to the ellipsoid, with the most precise being a geodetic reduction. However, surveyed lengths contain only five or six significant figures, typically. Thus, less strict methods can be applied to these short lengths. The elevation factor is computed as
In Equation (F.72), Re is the radius of the Earth, H the orthometric height, N the geoidal height, and h the geodetic height. All of these parameters are determined at the observation station. The relationship between the geodetic height, h, and orthometric height H is
In Equation (F.73), the radius in the azimuth of the line should be used for Re. Again since surveyors observe short distances typically, an average radius of the Earth of 6,371,000 m can be used in computing elevation factor. These approximations will be demonstrated in Example F.1.
In a map projection system, the scale factor computed using Equations (F.20), (F.29), or (F.42) is for a point. Generally, the scale factor changes continuously along the length of the line. Thus, a weighted mean using two endpoints of the line (k1 and k2) and midpoint (km) is a logical choice for computing a single scale factor for a line. It can be computed as
However, as with the elevation factor, this type of precision is seldom needed for the typical survey. Thus, the mean of the two endpoint scale factors is generally of sufficient accuracy for most surveys. In fact, it is not uncommon to use a single mean scale factor for an entire project.
As previously stated, the combined factor, CF, for the line is a product of the elevation factor (EF) and scale factor (kavg) and is computed as
Thus, a reduced grid distance, LGrid, is the product of the horizontal distance Lm and combined factor, CF, and is computed as
F.5.2 Reduction of Geodetic Azimuths
Figure F.2 depicts the differences between geodetic azimuths, T, and grid azimuths, t. Since grid north (GN) at a point is parallel to the central meridian, the convergence angle, γ, is the largest correction between the two geodetic and grid azimuths. Additionally, there is a small correction to convert the arc on an ellipsoid to its equivalent chord on the mapping surface. This is known as the arc-to-chord correction δ. The relationship between the geodetic azimuth and grid azimuth can be derived from Figure F.2 as
FIGURE F.2 Relationship of geodetic azimuth (T), grid azimuth (t), convergence angle (γ), and arc-to-chord correction (δ).
As shown in Figure F.2, this equation works whether the line is east or west of the central meridian. For the Lambert Conformal Conic map projection, the arc-to-chord correction is computed as
An analysis of Equation (F.78) shows that the worst cases for δ are for lines in the northern or southern extent of a map projection. Rearranging Equation (F.78) yields a change in longitude is
As an example, assume φ3 is 
. Furthermore, assume that the project is in the Pennsylvania North Zone, which has a sin φ0 of 0.661539733812. If δ is to be kept below 0.5″, then the maximum line in arc-seconds of longitude can be
At latitude 42°30′, this corresponds to a line of length of about 5334 ft or 1.6 km. Few surveyors in Northeastern Pennsylvania could find a line of this length to observe. Thus, the arc-to-chord correction is generally ignored in reductions, and Equation (F.77) can be simplified as
