3
Detection and Classification
Pattern classification is the act of assigning a class label to an object, a physical process or an event. The assignment is always based on measurements that are obtained from that object (or process, or event). The measurements are made available by a sensory system (see Figure 3.1). Table 3.1 provides some examples of application fields in which classification is the essential task.

Figure 3.1 Pattern classification.
Table 3.1 Some application fields of pattern classification
| Possible | ||
| Application field | measurements | Possible classes |
| Object classification | ||
| Sorting electronic parts | Shape, colour | ‘resistor’, ‘capacitor’, ‘transistor’, ‘IC’ |
| Sorting mechanical parts | Shape | ‘ring’, ‘nut’, ‘bolt’ |
| Reading characters | Shape | ‘A’, ‘B’, ‘C’ |
| Mode estimation in a physical process | ||
| Classifying manoeuvres of a vehicle | Tracked point features in an image sequence | ‘straight on’, ‘turning’ |
| Fault diagnosis in a combustion engine | Cylinder pressures, temperature, vibrations, acoustic emissions, crank angle resolver | ‘normal operation’, ‘defect fuel injector’, ‘defect air inlet valve’, ‘leaking exhaust valve’, |
| Event detection | ||
| Burglar alarm | Infrared | ‘alarm’, ‘no alarm’ |
| Food inspection | Shape, colour, temperature, mass, volume | ‘OK’, ‘NOT OK’ |
The definition of the set of relevant classes in a given application is in some cases given by the nature of the application, but in other cases the definition is not trivial. In the application ‘character reading for license plate recognition’, the choice of the classes does not need much discussion. However, in the application ‘sorting tomatoes into “class A”, “class B”, and “class C” ’ the definition of the classes is open for discussion. In such cases, the classes are defined by a generally agreed convention that the object is qualified according to the values of some attributes of the object, for example its size, shape and colour.
The sensory system measures some physical properties of the object that, hopefully, are relevant for classification. This chapter is confined to the simple case where the measurements are static, that is time independent. Furthermore, we assume that for each object the number of measurements is fixed. Hence, per object the outcomes of the measurements can be stacked to form a single vector, the so-called measurement vector. The dimension of the vector equals the number of measurements. The union of all possible values of the measurement vector is the measurement space. For some authors the word ‘feature’ is very close to ‘measurement’, but we will reserve that word for later use in Chapter 7.
The sensory system must be designed so that the measurement vector conveys the information needed to classify all objects correctly. If this is the case, the measurement vectors from all objects behave according to some pattern. Ideally, the physical properties are chosen such that all objects from one class form a cluster in the measurement space without overlapping the clusters formed by other classes.
Example 3.1 Classification of small mechanical parts Many workrooms have a spare part box where small, obsolete mechanical parts such as bolts, rings, nuts and screws are kept. Often, it is difficult to find a particular part. We would like to have the parts sorted out. For automated sorting we have to classify the objects by measuring some properties of each individual object. Then, based on the measurements we decide to what class that object belongs.
As an example, Figure 3.2(a) shows an image with rings, nuts, bolts and remaining parts, called scrap. These four types of objects will be classified by means of two types of shape measurements. The first type expresses to what extent the object is sixfold rotational symmetric. The second type of measurement is the eccentricity of the object. The image-processing technique that is needed to obtain these measurements is a topic that is outside the scope of this book.

Figure 3.2 Classification of mechanical parts: (a) image of various objects, (b) scatter diagram.
The two-dimensional (2D) measurement vector of an object can be depicted as a point in the 2D measurement space. Figure 3.2(b) shows the graph of the points of all objects. Since the objects in Figure 3.2(a) are already sorted manually, it is easy here to mark each point with a symbol that indicates the true class of the corresponding object. Such a graph is called a scatter diagram of the dataset.
The measure for sixfold rotational symmetry is suitable to discriminate between rings and nuts since rings and nuts have a similar shape except for the sixfold rotational symmetry of a nut. The measure for eccentricity is suitable to discriminate bolts from the nuts and the rings. The shapes of scrap objects are difficult to predict. Therefore, their measurements are scattered all over the space.
In this example the measurements are more or less clustered according to their true class. Therefore, a new object is likely to have measurements that are close to the cluster of the class to which the object belongs. Hence, the assignment of a class boils down to deciding to which cluster the measurements of the object belong. This can be done by dividing the 2D measurement space into four different partitions, one for each class. A new object is classified according to the partitioning to which its measurement vector points.
Unfortunately, some clusters are in each other's vicinity, or even overlapping. In these regions the choice of the partitioning is critical.
This chapter addresses the problem of how to design a pattern classifier. This is done within a Bayesian-theoretic framework. Section 3.1 discusses the general case. In Sections 3.1.1 and 3.1.2 two particular cases are dealt with. The so-called ‘reject option’ is introduced in Section 3.2. Finally, the two-class case, often called ‘detection’, is covered by Section 3.3.
3.1 Bayesian Classification
Probability theory is a solid base for pattern classification design. In this approach the pattern-generating mechanism is represented within a probabilistic framework. Figure 3.3 shows such a framework. The starting point is a stochastic experiment (Appendix C.1) defined by a set Ω = {ω1, …, ωK} of K classes. We assume that the classes are mutually exclusive. The probability P(ωk) of having a class ωk is called the prior probability. It represents the knowledge that we have about the class of an object before the measurements of that object are available. Since the number of possible classes is K, we have

The sensory system produces a measurement vector z with dimension N. Objects from different classes should have different measurement vectors. Unfortunately, the measurement vectors from objects within the same class also vary. For instance, the eccentricities of bolts in Figure 3.2 are not fixed since the shape of bolts is not fixed. In addition, all measurements are subject to some degree of randomness due to all kinds of unpredictable phenomena in the sensory system, for example quantum noise, thermal noise and quantization noise. The variations and randomness are taken into account by the probability density function of z.

Figure 3.3 Statistical pattern classification.
The conditional probability density function of the measurement vector z is denoted by P(z|ωK). It is the density of z coming from an object with known class ωk. If z comes from an object with unknown class, its density is indicated by p(z). This density is the unconditional density of z. Since classes are supposed to be mutually exclusive, the unconditional density can be derived from the conditional densities by weighting these densities by the prior probabilities:

The pattern classifier casts the measurement vector in the class that will be assigned to the object. This is accomplished by the so-called decision function ![]() that maps the measurement space on to the set of possible classes. Since z is an N-dimensional vector, the function maps
that maps the measurement space on to the set of possible classes. Since z is an N-dimensional vector, the function maps ![]() on to Ω, that is
on to Ω, that is ![]() .
.
Example 3.2 Probability densities of the ‘mechanical parts’ data Figure 3.4 is a graphical representation of the probability densities of the measurement data from Example 3.1. The unconditional density p (z) is derived from Equation (3.2) by assuming that the prior probabilities P(ωk) are reflected in the frequencies of occurrence of each type of object in Figure 3.3. In that figure, there are 94 objects with frequencies bolt:nut:ring:scrap = 20:28:27:19. Hence the corresponding prior probabilities are assumed to be 20/94, 28/94, 27/94 and 19/94, respectively.

Figure 3.4 Probability densities of the measurements shown in Figure 3.3. (a) The 3D plot of the unconditional density together with a 2D contour plot of this density on the ground plane. (b) 2D contour plots of the conditional probability densities.
The probabilities densities shown in Figure 3.4 are in fact not the real densities, buthey are estimates obtained from the samples. The topic of density estimation will be dealt with in Chapter 6. PRTools code to plot 2D-contours and 3D-meshes of a density is given Listing 3.1.
Listing 3.1 PRTools code for creating density plots
prload nutsbolts; % Load the dataset; see listing 5.1
w = gaussm(z,1); % Estimate a mixture of Gaussians
figure(1); scatterd (z); hold on;
plotm(w,6,[0.1 0.5 1.0]); % Plot in 3D
figure(2); scatterd (z); hold on;
for c = 1: 4
w = gaussm(seldat(z,c),1); % Estimate a Gaussian per class
plotm(w,2,[0.1 0.5 1.0]); % Plot in 2D
end;
In some cases, the measurement vectors coming from objects with different classes show some overlap in the measurement space. Therefore, it cannot always be guaranteed that the classification is free from mistakes. An erroneous assignment of a class to an object causes some damage, or some loss of value of the misclassified object, or an impairment of its usefulness. All this depends on the application at hand. For instance, in the application ‘sorting tomatoes into classes A, B or C’, having a class B tomato being misclassified as ‘class C’ causes a loss of value because a ‘class B’ tomato yields more profit than a ‘class C’ tomato. On the other hand, if a class C tomato is misclassified as a ‘class B’ tomato, the damage is much more since such a situation may lead to malcontent customers.
A Bayes classifier is a pattern classifier that is based on the following two prerequisites:
- The damage, or loss of value, involved when an object is erroneously classified can be quantified as a cost.
- The expectation of the cost is acceptable as an optimization criterion.
If the application at hand meets these two conditions, then the development of an optimal pattern classification is theoretically straightforward. However, the Bayes classifier needs good estimates of the densities of the classes. These estimates can be problematic to obtain in practice.
The damage, or loss of value, is quantified by a cost function (or loss function) ![]() . The function
. The function ![]() expresses the cost that is involved when the class assigned to an object is
expresses the cost that is involved when the class assigned to an object is ![]() while the true class of that object is ωk. Since there are K classes, the function C
while the true class of that object is ωk. Since there are K classes, the function C ![]() is fully specified by a K × K matrix. Therefore, sometimes the cost function is called a cost matrix. In some applications, the cost function might be negative, expressing the fact that the assignment of that class pays off (negative cost = profit).
is fully specified by a K × K matrix. Therefore, sometimes the cost function is called a cost matrix. In some applications, the cost function might be negative, expressing the fact that the assignment of that class pays off (negative cost = profit).
Example 3.3 Cost function of the mechanical parts application In fact, automated sorting of the parts in a ‘bolts-and-nuts’ box is an example of a recycling application. If we are not collecting the mechanical parts for reuse, these parts would be disposed of. Therefore, a correct classification of a part saves the cost of a new part, and thus the cost of such a classification is negative. However, we have to take into account that:
- The effort of classifying and sorting a part also has to be paid. This cost is the same for all parts regardless of its class and whether it has been classified correctly or not.
- A bolt that has been erroneously classified as a nut or a ring causes more trouble than a bolt that has been erroneously misclassified as scrap. Likewise arguments hold for a nut and a ring.
Table 3.2 is an example of a cost function that might be appropriate for this application.
Table 3.2 Cost function of the ‘sorting mechanical part’ application

The concepts introduced above, that is prior probabilities, conditional densities and cost function, are sufficient to design optimal classifiers. However, first another probability has to be derived: the posterior probability P(ωk|z). It is the probability that an object belongs to class ωk given that the measurement vector associated with that object is z. According to Bayes’ theorem for conditional probabilities (Appendix C.2) we have
If an arbitrary classifier assigns a class ![]() to a measurement vector z coming from an object with true class ωk then a cost
to a measurement vector z coming from an object with true class ωk then a cost ![]() is involved. The posterior probability of having such an object is P(ωk|z). Therefore, the expectation of the cost is
is involved. The posterior probability of having such an object is P(ωk|z). Therefore, the expectation of the cost is

This quantity is called the conditional risk. It expresses the expe-cted cost of the assignment ![]() to an object whose measurement vector is z.
to an object whose measurement vector is z.
From Equation (3.4) it follows that the conditional risk of a decision function ![]() is
is ![]() . The overall risk can be found by averaging the conditional risk over all possible measurement vectors:
. The overall risk can be found by averaging the conditional risk over all possible measurement vectors:
The integral extends over the entire measurement space. The quantity R is the overall risk (average risk or, briefly, risk) associated with the decision function ![]() . The overall risk is important for cost price calculations of a product.
. The overall risk is important for cost price calculations of a product.
The second prerequisite mentioned above states that the optimal classifier is the one with minimal risk R. The decision function that minimizes the (overall) risk is the same as the one that minimizes the conditional risk. Therefore, the Bayes classifier takes the form:
This can be expressed more briefly by
The expression argmin{} gives the element from Ω that minimizes R(ω|z). Substitution of Equations (3.3) and (3.4) yields

Pattern classification according to Equation (3.8) is called Bayesian classification or minimum risk classification.
Example 3.4 Bayes classifier for the mechanical parts application Figure 3.5(a) shows the decision boundary of the Bayes classifier for the application discussed in the previous examples. Figure 3.5(b) shows the decision boundary that is obtained if the prior probability of scrap is increased to 0.50 with an evenly decrease of the prior probabilities of the other classes. Comparing the results it can be seen that such an increase introduces an enlargement of the compartment for the scrap at the expense of the other compartments.

Figure 3.5 Bayes classification. (a) With prior probabilities: P (bolt) = 0:21, P (nut) = 0:30, P (ring) = 0:29, and P (scrap) = 0:20. (b) With increased prior probability for scrap: P (scrap) = 0:50. (c) With uniform cost function.
The overall risk associated with the decision function in Figure 3.5(a) appears to be −$0.092; the one in Figure 3.5(b) is −$0.036. The increase of cost (= decrease of profit) is due to the fact that scrap is unprofitable. Hence, if the majority of a bunch of objects consists of worthless scrap, recycling pays off less.
Listing 3.2 PRTools code for estimating decision boundaries taking account of the cost
prload nutsbolts;
cost = [ −0.20 0.07 0.07 0.07;…
0.07 −0.15 0.07 0.07;…
0.07 0.07 −0.05 0.07;…
0.03 0.03 0.03 0.03];
w1 = qdc(z); % Estimate a single Gaussian per class
% Change output according to cost
w2 = w1*classc*costm([],cost);
scatterd(z);
plotc(w1); % Plot without using cost
plotc(w2); % Plot using costThe total cost of all classified objects as given in Figure 3.5(a) appears to be –$8.98. Since the figure shows 94 objects, the average cost is –$8.98/94 = –$0.096. As expected, this comes close to the overall risk.
3.1.1 Uniform Cost Function and Minimum Error Rate
A uniform cost function is obtained if a unit cost is assumed when an object is misclassified and zero cost when the classification is correct. This can be written as
where δ(i, k) is the Kronecker delta function. With this cost function the conditional risk given in Equation (3.4) simplifies to

Minimization of this risk is equivalent to maximization of the posterior probability ![]() . Therefore, with a uniform cost function, the Bayes decision function (3.8) becomes the maximum a posteriori probability classifier (MAP classifier):
. Therefore, with a uniform cost function, the Bayes decision function (3.8) becomes the maximum a posteriori probability classifier (MAP classifier):
Application of Bayes’ theorem for conditional probabilities and cancellation of irrelevant terms yield a classification equivalent to a MAP classification but fully in terms of the prior probabilities and the conditional probability densities:
The functional structure of this decision function is given in Figure 3.6.

Figure 3.6 Bayes’ decision function with the uniform cost function (MAP classification).
Suppose that a class ![]() is assigned to an object with measurement vector z. The probability of having a correct classification is
is assigned to an object with measurement vector z. The probability of having a correct classification is ![]() . Consequently, the probability of having a classification error is
. Consequently, the probability of having a classification error is ![]() . For an arbitrary decision function
. For an arbitrary decision function ![]() , the conditional error probability is
, the conditional error probability is
This is the probability of an erroneous classification of an object whose measurement is z. The error probability averaged over all objects can be found by averaging e(z) over all the possible measurement vectors:
The integral extends over the entire measurement space. E is called the error rate and is often used as a performance measure of a classifier.
The classifier that yields the minimum error rate among all other classifiers is called the minimum error rate classifier. With a uniform cost function, the risk and the error rate are equal. Therefore, the minimum error rate classifier is a Bayes classifier with a uniform cost function. With our earlier definition of MAP classification we come to the following conclusion:
The conditional error probability of a MAP classifier is found by substitution of Equation (3.11) in (3.13):
The minimum error rate Emin follows from Equation (3.14):
Of course, phrases like ‘minimum’ and ‘optimal’ are strictly tied to the given sensory system. The performance of an optimal classification with a given sensory system may be less than the performance of a non-optimal classification with another sensory system.
Example 3.5 MAP classifier for the mechanical parts application Figure 3.5(c) shows the decision function of the MAP classifier. The error rate for this classifier is 4.8%, whereas the one of the Bayes classifier in Figure 3.5(a) is 5.3%. In Figure 3.5(c) four objects are misclassified. In Figure 3.5(a) that number is five. Thus, with respect to the error rate, the MAP classifier is more effective compared with the Bayes classifier of Figure 3.5(a). On the other hand, the overall risk of the classifier shown in Figure 3.5(c) and with the cost function given in Table 3.2 as −$0.084, this is a slight impairment compared with the –$0.092 of Figure 3.5(a).
3.1.2 Normal Distributed Measurements; Linear and Quadratic Classifiers
A further development of Bayes’ classification with the uniform cost function requires the specification of the conditional probability densities. This section discusses the case in which these densities are modelled as normal. Suppose that the measurement vectors coming from an object with class ωk are normally distributed with expectation vector µk and covariance matrix Ck (see Appendix C.3):

where N is the dimension of the measurement vector.
Substitution of Equation (3.17) in (3.12) gives the following minimum error rate classification:

We can take the logarithm of the function between braces without changing the result of the argmax{} function. Furthermore, all terms not containing k are irrelevant. Therefore Equation (3.18) is equivalent to

Hence, the expression of a minimum error rate classification with normally distributed measurement vectors takes the form of
where

A classifier according to Equation (3.20) is called a quadratic classifier and the decision function is a quadratic decision function. The boundaries between the compartments of such a decision function are pieces of quadratic hypersurfaces in the N-dimensional space. To see this, it suffices to examine the boundary between the compartments of two different classes, for example ωi and ωj. According to Equation (3.20) the boundary between the compartments of these two classes must satisfy the following equation:
or
Equation (3.23) is quadratic in z. In the case where the sensory system has only two sensors, that is N = 2, then the solution of (3.23) is a quadratic curve in the measurement space (an ellipse, a parabola, a hyperbola or a degenerated case: a circle, a straight line or a pair of lines). Examples will follow in subsequent sections. If we have three sensors, N = 3, then the solution of (3.23) is a quadratic surface (ellipsoid, paraboloid, hyperboloid, etc.). If N > 3, the solutions are hyperquadrics (hyperellipsoids, etc.).
If the number of classes is more than two, K > 2, then (3.23) is a necessary condition for the boundaries between compartments, but not a sufficient one. This is because the boundary between two classes may be intersected by a compartment of a third class. Thus, only pieces of the surfaces found by (3.23) are part of the boundary. The pieces of the surface that are part of the boundary are called decision boundaries. The assignment of a class to a vector exactly on the decision boundary is ambiguous. The class assigned to such a vector can be arbitrarily selected from the classes involved.
As an example we consider the classifications shown in Figure 3.5. In fact, the probability densities shown in Figure 3.4(b) are normal. Therefore, the decision boundaries shown in Figure 3.5 must be quadratic curves.
3.1.2.1 Class-Independent Covariance Matrices
In this subsection, we discuss the case in which the covariance matrices do not depend on the classes, that is Ck = C for all ωk ∈ Ω. This situation occurs when the measurement vector of an object equals the (class-dependent) expectation vector corrupted by sensor noise, that is ![]() . The noise n is assumed to be class-independent with covariance matrix C. Hence, the class information is brought forth by the expectation vectors only.
. The noise n is assumed to be class-independent with covariance matrix C. Hence, the class information is brought forth by the expectation vectors only.
The quadratic decision function of Equation (3.19) degenerates into
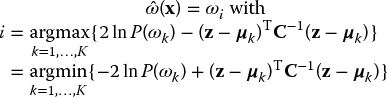
Since the covariance matrix C is self-adjoining and positive definite (Appendix B.5) the quantity ![]() can be regarded as a distance measure between the vector z and the expectation vector µk. The measure is called the squared Mahalanobis distance. The function of Equation (3.24) decides for the class whose expectation vector is nearest to the observed measurement vector (with a correction factor − 2ln P(ωk) to account for prior knowledge). Hence, the name minimum Mahalonobis distance classifier.
can be regarded as a distance measure between the vector z and the expectation vector µk. The measure is called the squared Mahalanobis distance. The function of Equation (3.24) decides for the class whose expectation vector is nearest to the observed measurement vector (with a correction factor − 2ln P(ωk) to account for prior knowledge). Hence, the name minimum Mahalonobis distance classifier.
The decision boundaries between compartments in the measurement space are linear (hyper) planes. This follows from Equations (3.20) and (3.21):
where
A decision function that has the form of Equation (3.25) is linear. The corresponding classifier is called a linear classifier. The equations of the decision boundaries are wi − wj + zT (wi − wj) = 0.
Figure 3.7 gives an example of a four-class problem (K = 4) in a two-dimensional measurement space (N = 2). A scatter diagram with the contour plots of the conditional probability densities are given (Figure 3.7(a)), together with the compartments of the minimum Mahalanobis distance classifier (Figure 3.7(b)). These figures were generated by the code in Listing 3.3.
Listing 3.3 PRTools code for minimum Mahalanobis distance classification
mus = [0.2 0.3; 0.35 0.75; 0.65 0.55; 0.8 0.25];
C = [0.018 0.007; 0.007 0.011];<b></b> z<b></b> = gauss(200,mus,C);
w = ldc(z); % Normal densities, identical covariances
figure(1); scatterd(z); hold on; plotm(w);
figure(2); scatterd(z); hold on; plotc(w);
Figure 3.7 Minimum Mahalanobis distance classification. (a) Scatter diagram with contour plot of the conditional probability densities. (b) Decision boundaries.
3.1.2.2 Minimum Distance Classification
A further simplification is possible when the measurement vector equals the class-dependent vector ![]() corrupted by class-independent white noise with covariance matrix C = σ2I:
corrupted by class-independent white noise with covariance matrix C = σ2I:
The quantity ![]() is the normal (Euclidean) distance bet-ween z and
is the normal (Euclidean) distance bet-ween z and ![]() . The classifier corresponding to Equation (3.27) decides for the class whose expectation vector is nearest to the observed measurement vector (with a correction factor − 2σ2log P(ωk) to account for the prior knowledge). Hence, the name minimum distance classifier. As with the minimum Mahalanobis distance classifier, the decision boundaries between compartments are linear (hyper) planes. The plane separating the compartments of two classes ωi and ωj is given by
. The classifier corresponding to Equation (3.27) decides for the class whose expectation vector is nearest to the observed measurement vector (with a correction factor − 2σ2log P(ωk) to account for the prior knowledge). Hence, the name minimum distance classifier. As with the minimum Mahalanobis distance classifier, the decision boundaries between compartments are linear (hyper) planes. The plane separating the compartments of two classes ωi and ωj is given by
The solution of this equation is a plane perpendicular to the line segment connecting ![]() and
and ![]() . The location of the hyperplane depends on the factor σ2log (P(ωi)/P(ωj)). If P(ωi) = P(ωj), the hyperplane is the perpendicular bisector of the line segment (see Figure 3.8).
. The location of the hyperplane depends on the factor σ2log (P(ωi)/P(ωj)). If P(ωi) = P(ωj), the hyperplane is the perpendicular bisector of the line segment (see Figure 3.8).

Figure 3.8 Decision boundary of a minimum distance classifier.
Figure 3.9 gives an example of the decision function of the minimum distance classification. PRTools code to generate these figures is given in Listing 3.4.
Listing 3.4 PRTools code for the minimum distance classification
mus = [0.2 0.3; 0.35 0.75; 0.65 0.55; 0.8 0.25];
C = 0.01*eye(2);<b></b> z<b></b> = gauss(200,mus,C);
% Normal densities, uncorrelated noise with equal variances
w = nmsc(z);
figure (1); scatterd (z); hold on; plotm (w);
figure (2); scatterd (z); hold on; plotc (w);
Figure 3.9 Minimum distance classification. (a) Scatter diagram with a contour plot of the conditional probability densities. (b) Decision boundaries.
3.1.2.3 Class-Independent Expectation Vectors
Another interesting situation is when the class information is solely brought forth by the differences between covariance matrices. In that case, the expectation vectors do not depend on the class: ![]() for all k. Hence, the central parts of the conditional probability densities overlap. In the vicinity of the expectation vector, the probability of making a wrong decision is always largest. The decision function takes the form of
for all k. Hence, the central parts of the conditional probability densities overlap. In the vicinity of the expectation vector, the probability of making a wrong decision is always largest. The decision function takes the form of

If the covariance matrices are of the type σ2kI, the decision boundaries are concentric circles or (hyper) spheres. Figure 3.10(a) gives an example of such a situation. If the covariance matrices are rotated versions of one prototype, the decision boundaries are hyperbolae. If the prior probabilities are equal, these hyperbolae degenerate into a number of linear planes (or, if N = 2, linear lines). An example is given in Figure 3.10(b).

Figure 3.10 Classification of objects with equal expectation vectors. (a) Rotational symmetric conditional probability densities. (b) Conditional probability densities with different orientations (see text).
3.2 Rejection
Sometimes it is advantageous to provide the classification with a so-called reject option. In some applications, an erroneous decision may lead to very high cost, or even to a hazardous situation. Suppose that the measurement vector of a given object is in the vicinity of the decision boundary. The measurement vector does not provide much class information then. Therefore, it might be beneficial to postpone the classification of that particular object. Instead of classifying the object, we reject the classification. On rejection of a classification we have to classify the object either manually or by means of more involved techniques (for instance, by bringing in more sensors or more advanced classifiers).
We may take the reject option into account by extending the range of the decision function by a new element: the rejection class ω0. The range of the decision function becomes ![]() . The decision function itself is a mapping
. The decision function itself is a mapping ![]() . In order to develop a Bayes classifier, the definition of the cost function must also be extended:
. In order to develop a Bayes classifier, the definition of the cost function must also be extended: ![]() . The definition is extended so as to express the cost of rejection. C(ω0|ωk) is the cost of rejection while the true class of the object is ωk.
. The definition is extended so as to express the cost of rejection. C(ω0|ωk) is the cost of rejection while the true class of the object is ωk.
With these extensions, the decision function of a Bayes classifier becomes (see Equation (3.8))

The further development of the classifier follows the same course as in Equation (3.8).
3.2.1 Minimum Error Rate Classification with Reject Option
The minimum error rate classifier can also be extended with a reject option. Suppose that the cost of a rejection is Crej regardless of the true class of the object. All other costs are uniform and defined by Equation (3.9).
We first note that if the reject option is chosen, the risk is Crej. If it is not, the minimal conditional risk is the emin (z) given by Equation (3.15). Minimization of Crej and emin (z) yields the following optimal decision function:

The maximum posterior probability max {P(ω|z)} is always greater than or equal to 1/K. Therefore, the minimal conditional error probability is bounded by (1 – 1/K). Consequently, in Equation (3.31) the reject option never wins if Crej ≥ 1 − 1/K.
The overall probability of having a rejection is called the reject rate. It is found by calculating the fraction of measurements that fall inside the reject region:

The integral extends over those regions in the measurement space for which Crej < e(z). The error rate is found by averaging the conditional error over all measurements except those that fall inside the reject region:

Comparison of Equation (3.33) with (3.16) shows that the error rate of a classification with a reject option is bounded by the error rate of a classification without a reject option.
Example 3.6 The reject option in the mechanical parts application In the classification of bolts, nuts, rings and so on, discussed in the previous examples, it might be advantageous to manually inspect those parts whose automatic classification is likely to fail. We assume that the cost of manual inspection is about $0.04. Table 3.3 tabulates the cost function with the reject option included (compare with Table 3.2).
The corresponding classification map is shown in Figure 3.11. In this example, the reject option is advantageous only between the regions of the rings and the nuts. The overall risk decreases from –$0.092 per classification to –$0.093 per classification. The benefit of the reject option is only marginal because the scrap is an expensive item when offered to manual inspection. In fact, the assignment of an object to the scrap class is a good alternative for the reject option.
Table 3.3 Cost function of the mechanical part application with the reject option included


Figure 3.11 Bayes’ classification with the reject option included.
Listing 3.5 shows the actual implementation in Matlab®. Clearly it is very similar to the implementation for the classification including the costs. To incorporate the reject option, not only does the cost matrix need to be extended but clabels has to be redefined as well. When these labels are not supplied explicitly, they are copied from the dataset. In the reject case, an extra class is introduced, so the definition of the labels cannot be avoided.
Listing 3.5 PRTools codes for a minimum risk classification including a reject option
prload nutsbolts;
cost=[ −0.20 0.07 0.07 0.07; …
0.07 −0.15 0.07 0.07; …
0.07 0.07 −0.05 0.07; …
0.03 0.03 0.03 0.03; …
−0.16 −0.11 0.01 0.07];
clabels=str2mat (getlablist(z),‘reject’);
w1=qdc(z); % Estimate a single Gaussian per class
scatterd(z);
% Change output according to cost
w2=w1*classc*costm([],cost’,clabels);
plotc(w1); % Plot without using cost
plotc(w2); % Plot using cost3.3 Detection: The Two-Class Case
The detection problem is a classification problem with two possible classes: K = 3. In this special case, the Bayes decision rule can be moulded into a simple form. Assuming a uniform cost function, the MAP classifier, expressed in Equation (3.12), reduces to the following test:
If the test fails, it is decided for ω2, otherwise for ω1. We write symbolically:

Smaller type for ω1 and ω2 in 3.35 and 3.39 at top and bottom (see 3.36).
Rearrangement gives
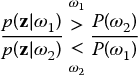
Regarded as a function of ωk the conditional probability density p(z|ωk) is called the likelihood function of ωk. Therefore, the ratio
is called the likelihood ratio. With this definition the classification becomes a simple likelihood ratio test:

The test is equivalent to a threshold operation applied to L(z) with the threshold P(ω2)/P(ω1).
Even if the cost function is not uniform, the Bayes detector retains the structure of (3.38); only the threshold should be adapted so as to reflect the change of cost. The proof of this is left as an exercise for the reader.
In case of measurement vectors with normal distributions, it is convenient to replace the likelihood ratio test with a so-called log-likelihood ratio test:

For vectors drawn from normal distributions, the log-likelihood ratio is

which is much easier than the likelihood ratio. When the covariance matrices of both classes are equal (C1 = C2 = C) the log-likelihood ratio simplifies to
Two types of errors are involved in a detection system. Suppose that ![]() is the result of a decision based on the measurement z. The true (but unknown) class ω of an object is either ω1 or ω2. Then the following four states may occur:
is the result of a decision based on the measurement z. The true (but unknown) class ω of an object is either ω1 or ω2. Then the following four states may occur:
| ω = ω1 | ω = ω2 | |
| Correct decision I | Type II error | |
| Type I error | Correct decision II |
Often a detector is associated with a device that decides whether an object is present (ω = ω2) or not (ω = ω1), or that an event occurs or not. These types of problems arise, for instance, in radar systems, medical diagnostic systems, burglar alarms, etc. Usually, the nomenclature for the four states is then as follows:
| ω = ω1 | ω = ω2 | |
| True negative | Missed event or false negative | |
| False alarm or false positive | Detection (or hit) or true positive |
Sometimes, the true negative is called ‘rejection’. However, we have reserved this term for Section 3.2, where it has a different denotation.
The probabilities of the two types of errors, that is the false alarm and the missed event, are performance measures of the detector. Usually these probabilities are given conditionally with respect to the true classes, that is ![]() and
and ![]() . In addition, we may define the probability of a detection
. In addition, we may define the probability of a detection ![]() .
.
The overall probability of a false alarm can be derived from the prior probability using Bayes’ theorem, for example ![]() . The probabilities Pmiss and Pfa as a function of the threshold T follow from (3.39):
. The probabilities Pmiss and Pfa as a function of the threshold T follow from (3.39):

In general, it is difficult to find analytical expressions for Pmiss(T) and Pfa(T). In the case of Gaussian distributed measurement vectors, with C1 = C2 = C (see Figure 3.12), expression (3.42) can be further developed. Equation (3.41) shows that Λ(z) is linear in z. Since z has a normal distribution, so has Λ(z) (see Appendix C.3.1). The posterior distribution of Λ(z) is fully specified by its conditional expectation and its variance. As Λ(z) is linear in z, these parameters are obtained as

Figure 3.12 The conditional probability densities of the log-likelihood ratio in the Gaussian case with C1 = C2 = C.

Likewise
and
With that, the signal-to-noise ratio is

The quantity ![]() is the squared Mahalanobis distance between
is the squared Mahalanobis distance between ![]() and
and ![]() with respect to C. The square root,
with respect to C. The square root, ![]() is called the discriminability of the detector. It is the signal-to-noise ratio expressed as an amplitude ratio.
is called the discriminability of the detector. It is the signal-to-noise ratio expressed as an amplitude ratio.
The conditional probability densities of Λ are shown in Figure 3.13. The two overlapping areas in this figure are the probabilities of false alarm and missed event. Clearly, these areas decrease as d increases. Therefore, d is a good indicator of the performance of the detector.

Figure 3.13 Performance of a detector in the Gaussian case with equal covariance matrices. (a) Pmiss, Pdet and Pfa versus the threshold T. (b) Pdet versus Pfa as a parametric plot of T.
Knowing that the conditional probabilities are Gaussian, it is possible to evaluate the expressions for Pmiss(T) and Pfa(T) in (3.42) analytically. The distribution function of a Gaussian random variable is given in terms of the error function erf ():

Figure 3.13(a) shows a graph of Pmiss, Pfa and Pdet = 1 − Pmiss when the threshold T varies. It can be seen that the requirements for T are contradictory. The probability of a false alarm (type I error) is small if the threshold is chosen to be small. However, the probability of a missed event (type II error) is small if the threshold is chosen to be large. A trade-off must be found between both types of errors.
The trade-off can be made explicitly visible by means of a parametric plot of Pdet versus Pfa with varying T. Such a curve is called a receiver operating characteristic curve (ROC curve). Ideally, Pfa = 0 and Pdet = 1, but the figure shows that no threshold exists for which this occurs. Figure 3.13(b) shows the ROC curve for a Gaussian case with equal covariance matrices. Here, the ROC curve can be obtained analytically, but in most other cases the ROC curve of a given detector must be obtained either empirically or by numerical integration of (3.42).
In Listing 3.6 the Matlab® implementation for the computation of the ROC curve is shown. To avoid confusion about the roles of the different classes (which class should be considered positive and which negative) in PRTools the ROC curve shows the fraction false positive and false negative. This means that the resulting curve is a vertically mirrored version of Figure 3.13(b). Note also that in the listing the training set is used to both train a classifier and to generate the curve. To have a reliable estimate, an independent dataset should be used for estimation of the ROC curve.
Listing 3.6 PRTools code for estimation of a ROC curve
z = gendats(100,1,2); % Generate a 1D dataset
w = qdc(z); % Train a classifier
r = roc(z*w); % Compute the ROC curve
plotr(r); % Plot itThe merit of an ROC curve is that it specifies the intrinsic ability of the detector to discriminate between the two classes. In other words, the ROC curve of a detector depends neither on the cost function of the application nor on the prior probabilities.
Since a false alarm and a missed event are mutually exclusive, the error rate of the classification is the sum of both probabilities:

In the example of Figure 3.13, the discriminability d equals ![]() . If this indicator becomes larger, Pmiss and Pfa become smaller. Hence, the error rate E is a monotonically decreasing function of d.
. If this indicator becomes larger, Pmiss and Pfa become smaller. Hence, the error rate E is a monotonically decreasing function of d.
Example 3.7 Quality inspection of empty bottles In the bottling industry, the detection of defects of bottles (to be recycled) is relevant in order to assure the quality of the product. A variety of flaws can occur: cracks, dirty bottoms, fragments of glass, labels, etc. In this example, the problem of detecting defects of the mouth of an empty bottle is addressed. This is important, especially in the case of bottles with crown caps. Small damages of the mouth may cause a non-airtight enclosure of the product which subsequently causes an untimely decay.
The detection of defects at the mouth is a difficult task. Some irregularities at the mouth seem to be perturbing, but in fact are harmless. Other irregularities (e.g. small intrusions at the surface of the mouth) are quite harmful. The inspection system (Figure 3.14) that performs the task consists of a stroboscopic, specular ‘light field’ illuminator, a digital camera, a detector, an actuator and a sorting mechanism. The illumination is such that in the absence of irregularities at the mouth, the bottle is seen as a bright ring (with fixed size and position) on a dark background. Irregularities at the mouth give rise to disturbances of the ring (see Figure 3.15).

Figure 3.14 Quality inspection system for the recycling of bottles.

Figure 3.15 Acquired images of two different bottles. (a) Image of the mouth of a new bottle. (b) Image of the mouth of an older bottle with clearly visible intrusions.
The decision of the inspection system is based on a measurement vector that is extracted from the acquired image. For this purpose the area of the ring is divided into 256 equally sized sectors. Within each sector the average of the grey levels of the observed ring is estimated. These averages (as a function of the running arc length along the ring) are made rotational invariant by a translation invariant transformation, for example the amplitude spectrum of the discrete Fourier transform.
The transformed averages form the measurement vector z. The next step is the construction of a log-likelihood ratio Λ(z) according to Equation (3.40). Comparing the likelihood ratio against a suitable threshold value gives the final decision.
Such a detector should be trained with a set of bottles that are manually inspected so as to determine the parameters ![]() , etc. (see Chapter 6). Another set of manually inspected bottles is used for evaluation. The result for a particular application is shown in Figure 3.16.
, etc. (see Chapter 6). Another set of manually inspected bottles is used for evaluation. The result for a particular application is shown in Figure 3.16.

Figure 3.16 Estimated performance of the bottle inspector. (a) The conditional probability densities of the log-likelihood ratio. (b) The ROC curve.
It seems that the Gaussian assumption with equal covariance matrices is appropriate here. The discriminability appears to be d = 4.8.
3.4 Selected Bibliography
Many good textbooks on pattern classification have been written. These books go into more detail than is possible here and approach the subject from different points of view. The following list is a selection.
- Duda, R.O., Hart, P.E. and Stork, D.G., Pattern Classification, John Wiley & Sons, Ltd, London, UK, 2001.
- Fukanaga, K., Statistical Pattern Recognition, Academic Press, New York, NY, 1990.
- Ripley, B.D., Pattern Recognition and Neural Networks, Cambridge University Press, Cambridge, UK, 1996.
- Webb, A.R., Statistical Pattern Recognition, 2nd edition, John Wiley & Sons, Ltd, London, UK, 2003.
Exercises
-
Give at least two more examples of classification systems. Also define possible measurements and the relevant classes. (0)
-
Give a classification problem where the class definitions are subjective. (0)
-
Assume we have three classes of tomato with decreasing quality, class ‘A’, class ‘B’ and class ‘C’. Assume further that the cost of misclassifying a tomato to a higher quality is twice as expensive as vice versa. Give the cost matrix. What extra information do you need in order to fully determine the matrix? (0)
-
Assume that the number of scrap objects in Figure 3.2 is actually twice as large. How should the cost matrix, given in Table 3.2, be changed, such that the decision function remains the same? (0)
-
What quantities do you need to compute the Bayes classifier? How would you obtain these quantities? (0)
-
Derive a decision function assuming that objects come from normally distributed classes as in Section 3.1.2, but now with an arbitrary cost function (*).
-
Can you think of a physical measurement system in which it can be expected that the class distributions are Gaussian and where the covariance matrices are independent of the class? (0)
-
Construct the ROC curve for the case that the classes have no overlap and classes that are completely overlapping. (0)
-
Derive how the ROC curve changes when the class prior probabilities are changed. (0)
-
Reconstruct the class conditional probabilities for the case that the ROC curve is not symmetric around the axis which runs from (1, 0) to (0, 1). (0)
