3.4. Modeling Cameras

This chapter deals with the task of building a mathematical model of a camera. We give a mathematical model of the standard pinhole camera and define intrinsic and extrinsic parameters. For more detailed treatment, see [24, 15], and for a different approach see [26].

3.4.1. The pinhole camera

The simplest optical system used for modeling cameras is the pinhole camera. The camera is modeled as a box with a small hole in one of the sides and a photographic plate at the opposite side; see Figure 3.6. Introduce a coordinate system as in Figure 3.6. Observe that the origin of the coordinate system is located at the center of projection, the focal point, and that the z-axis coincides with the optical axis. The distance from the focal point to the image, f, is called the focal length. Similar triangles give

Equation 3.5

This equation can be written in matrix form, using homogeneous coordinates, as

Equation 3.6

where the depth, λ, is equal to Z.

3.4.2. The camera matrix

Introducing the notation

Equation 3.7

in (3.6) gives

Equation 3.8

where P = K[I_3x3 | 0_3x1].

Definition 22. A 3 x 4 matrix P relating extended image coordinates x = (x, y, 1) to extended object coordinates X = (X, Y, Z, 1) via the equation

is called a camera matrix, and the equation above is called the camera equation. ▪

Observe that the focal point is given as the right nullspace to the camera matrix, since PC = 0, where C denote homogeneous coordinates for the focal point, C.

3.4.3. The intrinsic parameters

In a refined camera model, the matrix K in (3.7) is replaced by

Equation 3.9

where the parameters have the following interpretations, see Figure 3.7:

- f: focal length, also called camera constant

- γ: aspect ratio, modeling nonquadratic light-sensitive elements

- s : skew, modeling nonrectangular light-sensitive elements

- (x₀, y₀) : principal point, orthogonal projection of the focal point onto the image plane; see Figure 3.6.

These parameters are called the intrinsic parameters, since they model intrinsic properties of the camera. For most cameras, s = 0 and γ ≈ 1 and the principal point is located close to the center of the image.

Definition 23. A camera is said to be calibrated if K is known. Otherwise, it is said to be uncalibrated. ▪

3.4.4. The extrinsic parameters

It is often advantageous to be able to express object coordinates in a different coordinate system than the camera coordinate system. This is especially the case when the relation between these coordinate systems is not known. For this purpose, it is necessary to model the relation between two different coordinate systems in 3D. The natural way to do this is to model the relation as a Euclidean transformation. Denote the camera coordinate system with e_c and points expressed in this coordinate system with index c-for example, (X_c, Y_c, Z_c)-and similarly denote the object coordinate system with e₀ and points expressed in this coordinate system with index o; see Figure 3.8. A

Euclidean transformation from the object coordinate system to the camera coordinate system can be written in homogeneous coordinates as

Equation 3.10

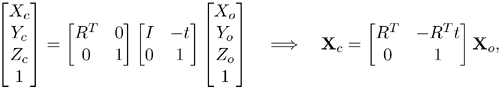
where R denotes an orthogonal matrix and t a vector, encoding the rotation and translation in the rigid transformation. Observe that the focal point (0, 0, 0) in the c-system corresponds to the point t in the o-system. Inserting (3.10) in (3.8), taking into account that X in (3.8) is the same as X_c in (3.10), we obtain

Equation 3.11

with P = KR^T[I| - t]. Usually, it is assumed that object coordinates are expressed in the object coordinate system and the index o in X₀ is omitted. Observe that the focal point, C_f = t = (t_x, t_y, t_z), is given from the right nullspace to P according to

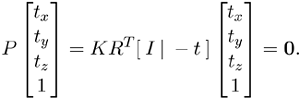
Given a camera, described by the camera matrix P, this camera could also be described by the camera matrix μP, 0 ≠μ ∊ , since these give the same image point for each object point. This means that the camera matrix is only defined up to an unknown scale factor. Moreover, the camera matrix P can be regarded as a projective transformation from ³ to ²; see (3.8) and (3.4).

Observe also that replacing t with μt and (X, Y, Z) with (μX, μY, μZ), 0 ≠ μ ∊ , gives the same image since

We refer to this ambiguity as the scale ambiguity.

We can now calculate the number of parameters in the camera matrix, P:

- K: 5 parameters (ƒ, γ, s, x₀, y₀)

- R: 3 parameters

- t: 3 parameters

Summing up gives a total of 11 parameters, which is the same as in a general 3 × 4 matrix defined up to scale. This means that for an uncalibrated camera, the factorization P = KR^T [I | - t] has no meaning, and we can instead deal with P as a general 3 × 4 matrix.

Given a calibrated camera with camera matrix P = KR^T [ I | – t] and corresponding camera equation

it is often advantageous to make a change of coordinates from x to in the image according to x = K, which gives

Now the camera matrix becomes

Definition 24. A camera represented with a camera matrix of the form

is called a normalized camera. ▪

Note that even when K is only approximatively known, the above normalization can be useful for numerical reasons. This is discussed more in detail in Section 3.7.

3.4.5. Properties of the pinhole camera

We conclude this section with some properties of the pinhole camera.

Proposition 4. The set of 3D points that project to an image point, x, is given by

where C denotes the focal point in homogeneous coordinates and P⁺ denotes the pseudo-inverse of P.

Proposition 5. The set of 3D-points that projects to a line, 1, is the points lying on the plane Π = P^T 1.

Proof: It is obvious that the set of points lie on the plane defined by the focal point and the line 1. A point x on 1 fulfills x^Tl = 0 and a point X on the plane Π fulfills Π^TX = 0. Since x ~ PX, we have (PX)^T1 = X^T P^T1 = 0 and identification with Π^TX = 0 gives Π = P^T1. ▪

Lemma 3. The projection of a quadric, X^TCX = 0 (dually Π^T C'Π = 0, C' = C^–1), is an image conic, x^Tcx = 0 (dually 1^Tc'1 = 0, c^' = c^–1), with c' = PC' P^T.

Proof: Use the previous proposition. ▪

Proposition 6. The image of the absolute conic is given by the conic x^Tωx = 0 (dually 1^Tω'1 = 0), where ω' = KK^T.

Proof: The result follows from the previous lemma:

▪