4.1.1 Electrical Equations of a Synchronous Machine

Based on the stator and rotor equivalent circuits, voltage equations can be obtained in terms of flux linkages and winding resistances [17]. According to Faraday’s and Kirchhoff’s laws

$v=Ri+\frac{d\mathrm{\Psi }}{dt}.$

Neglecting saturation the flux linkages are proportional to the currents; thus

$\mathrm{\Psi }=Li.$

Substitution of Eq. 4-2 into Eq. 4-1 yields – after solving for dΨ/dt – the differential equation

$\frac{d\mathrm{\Psi }}{dt}=v-R{L}^{-1}\mathrm{\Psi }.$

However, it is required to take into account the interaction between self- and mutual inductances of the windings residing on the stator and rotor members. Thus, a set of differential equations can be written in matrix form for the stator and rotor circuits as

$v_{\mathit{abc}}=R_S{i}_{\mathit{abc}}+p{\mathrm{\Psi }}_{\mathit{abc}}\text{,}$

$v_{fdq}=R_R{i}_{fdq}+p{\mathrm{\Psi }}_{fdq}\text{,}$

where subscripts abc and fdq represent the stator (e.g., abc components) and rotor (e.g., field, d- and q-axes components), respectively, and p is the differential operator.

The matrix equation for the flux linkages is

$\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_{\mathit{abc}}\hfill \\ \hfill {\mathrm{\Psi }}_{fdq}\hfill \end{array}\right]=\left[L\right]\left[\begin{array}{c}\hfill i_{\mathit{abc}}\hfill \\ \hfill i_{fdq}\hfill \end{array}\right].$

In Eqs. 4-1 to 4-6:

$\begin{array}{l}p\mathrm{\Psi }=p{\left[{\mathrm{\Psi }}_{\mathit{abc}}{\mathrm{\Psi }}_{fdq}\right]}^T=p[{\mathrm{\Psi }}_a{\mathrm{\Psi }}_b{\mathrm{\Psi }}_c{\mathrm{\Psi }}_f\\ {\mathrm{\Psi }}_{kd1}\dots {\mathrm{\Psi }}_{kdn}{\mathrm{\Psi }}_{kq1}\dots {\mathrm{\Psi }}_{kqn}]{}^T\text{,}\end{array}$

$\begin{array}{l}v={\left[v_{\mathit{abc}}{v}_{fdq}\right]}^T=[v_a{v}_b{v}_c{v}_f{v}_{kd1}\dots \\ v_{kdn}{v}_{kq1}\dots v_{kqn}]{}^T\text{,}\end{array}$

$i={\left[i_{\mathit{abc}}{i}_{fdq}\right]}^T={\left[i_a{i}_b{i}_c{i}_f{i}_{kd1}\dots i_{kdn}{i}_{kq1}\dots i_{kqn}\right]}^T\text{,}$

$R=\mathrm{diag}{\left[R_a{R}_b{R}_c{F}_f{R}_{kd1}\cdots R_{kdn}{R}_{kq1}\cdots R_{kqn}\right]}^T\text{,}$

where kdn and kqn are the number of damper windings of the d- and q-axes, respectively. The inductance matrix L has the form

$\left[L\right]=\left[\begin{array}{cc}\hfill L_{SS}\hfill & \hfill L_{SR}\hfill \\ \hfill L_{RS}\hfill & \hfill L_{RR}\hfill \end{array}\right].$

L_SS are stator self-inductances, L_SR are stator–rotor mutual inductances, where L_SR = [L_RS]^T, and L_RR are rotor self-inductances. T indicates the transpose of a matrix. Note that L_SS, L_SR, and L_RS consist of time-varying inductances representing the interrelationships between the stator and rotor windings as a function of the rotor position angle θ.

Therefore, the inductance matrix is a function of time due to θ which itself is a function of time (e.g., θ = ω_rt + δ – π/2, where ω_r and δ are rotor angular velocity and rotor angle, respectively):

$L=\left[\begin{array}{llllllll}{L}_{\mathit{aa}}\hfill & L_{\mathit{ab}}\hfill & L_{ac}\hfill & L_{af}\hfill & L_{akd}\hfill & L_{akq}\hfill & L_{akD}\hfill & L_{akQ}\hfill \\ L_{\mathit{ba}}\hfill & L_{bb}\hfill & L_{bc}\hfill & L_{bf}\hfill & L_{bkd}\hfill & L_{bkq}\hfill & L_{fkD}\hfill & L_{bkQ}\hfill \\ L_{ca}\hfill & L_{cb}\hfill & L_{\mathit{cc}}\hfill & L_{cf}\hfill & L_{ckd}\hfill & L_{ckq}\hfill & L_{ckD}\hfill & L_{ckQ}\hfill \\ L_{fa}\hfill & L_{fb}\hfill & L_{\mathit{fc}}\hfill & L_{\mathit{ff}}\hfill & L_{fkd}\hfill & 0\hfill & L_{fkD}\hfill & 0\hfill \\ L_{kda}\hfill & L_{kdb}\hfill & L_{kdc}\hfill & L_{kdf}\hfill & L_{kkd}\hfill & 0\hfill & L_{\mathit{kdkD}}\hfill & 0\hfill \\ L_{kqa}\hfill & L_{kqd}\hfill & L_{kqc}\hfill & 0\hfill & 0\hfill & L_{kkq}\hfill & 0\hfill & L_{\mathit{kqkQ}}\hfill \\ L_{\mathit{kDa}}\hfill & L_{kDb}\hfill & L_{kDc}\hfill & L_{kDf}\hfill & L_{\mathit{kDkd}}\hfill & 0\hfill & L_{kkD}\hfill & 0\hfill \\ L_{kQa}\hfill & L_{kQb}\hfill & L_{kQc}\hfill & 0\hfill & 0\hfill & L_{\mathit{kQkq}}\hfill & 0\hfill & L_{kkQ}\hfill \end{array}\right]$

In the above equations, only two damper windings along the d- and q-axes are assumed and [17]:

• The entries of L_RR represent – neglecting saturation – constant inductances, independent of the rotor position θ. L_RR has the form

$L_{RR}=\left[\begin{array}{lllll}{L}_{\mathit{ff}}\hfill & L_{fkd}\hfill & 0\hfill & L_{fdD}\hfill & 0\hfill \\ L_{kdf}\hfill & L_{kkd}\hfill & 0\hfill & L_{\mathit{kdkD}}\hfill & 0\hfill \\ 0\hfill & 0\hfill & L_{kkq}\hfill & 0\hfill & L_{\mathit{kqkQ}}\hfill \\ L_{kDf}\hfill & L_{\mathit{kDkd}}\hfill & 0\hfill & L_{kkD}\hfill & 0\hfill \\ 0\hfill & 0\hfill & L_{\mathit{kQkq}}\hfill & 0\hfill & L_{kkQ}\hfill \end{array}\right].$

• Considering even harmonics (h) up to the nth order, L_SS has the form

$L_{SS}=\left[\begin{array}{ccc}\hfill L_{{\mathit{aa}}_0}+{\displaystyle \sum _{h=2}^n{L}_{a{a}_h}cosh\theta }\hfill & \hfill -L_{a{b}_0}-{\displaystyle \sum _{h=2}^n{L}_{a{b}_h}cosh\left(\theta +\frac{\pi }{6}\right)}\hfill & \hfill -L_{a{c}_0}-{\displaystyle \sum _{h=2}^n{L}_{a{c}_h}cosh\left(\theta +\frac{5\pi }{6}\right)}\hfill \\ \hfill -L_{{\mathit{ba}}_0}-{\displaystyle \sum _{h=2}^n{L}_{b{a}_h}cosh\left(\theta +\frac{\pi }{6}\right)}\hfill & \hfill L_{b{b}_0}+{\displaystyle \sum _{h=2}^n{L}_{b{b}_h}cosh\left(\theta -\frac{2\pi }{3}\right)}\hfill & \hfill -L_{b{c}_0}-{\displaystyle \sum _{h=2}^n{L}_{b{c}_h}cosh\left(\theta -\frac{\pi }{2}\right)}\hfill \\ \hfill -L_{{ac}_0}-{\displaystyle \sum _{h=2}^n{L}_{a{c}_h}cosh\left(\theta +\frac{5\pi }{6}\right)}\hfill & \hfill -L_{a{c}_0}-{\displaystyle \sum _{h=2}^n{L}_{c{b}_h}cosh\left(\theta -\frac{\pi }{2}\right)}\hfill & \hfill L_{c{c}_0}+{\displaystyle \sum _{h=2}^n{L}_{c{c}_h}cosh\left(\theta +\frac{2\pi }{3}\right)}\hfill \end{array}\right].$

• Considering odd harmonics (h) up to the mth order, L_SR has the form

$L_{SR}=\left[\begin{array}{ccccc}{\displaystyle \sum _{h=1}^m{M}_{f_h}cosh\theta }\hfill & {\displaystyle \sum _{h=1}^m{M}_{k{d}_h}cosh\theta }\hfill & -{\displaystyle \sum _{h=1}^m{M}_{k{q}_h}cosh\theta }\hfill & {\displaystyle \sum _{h=1}^m{M}_{k{D}_h}cosh\theta }\hfill & -{\displaystyle \sum _{h=1}^m{M}_{k{Q}_h}cosh\theta }\hfill \\ \hfill {\displaystyle \sum _{h=1}^m{M}_{f_h}cosh\left(\theta -\frac{2\pi }{3}\right)}\hfill & \hfill {\displaystyle \sum _{h=1}^m{M}_{k{d}_h}cosh\left(\theta -\frac{2\pi }{3}\right)}\hfill & \hfill -{\displaystyle \sum _{h=1}^m{M}_{k{q}_h}cosh\left(\theta -\frac{2\pi }{3}\right)}\hfill & \hfill {\displaystyle \sum _{h=1}^m{M}_{k{D}_h}cosh\left(\theta -\frac{2\pi }{3}\right)}\hfill & \hfill -{\displaystyle \sum _{h=1}^m{M}_{k{Q}_h}cosh\left(\theta -\frac{2\pi }{3}\right)}\hfill \\ \hfill {\displaystyle \sum _{h=1}^m{M}_{f_h}cosh\left(\theta +\frac{2\pi }{3}\right)}\hfill & \hfill {\displaystyle \sum _{h=1}^m{M}_{k{d}_h}cosh\left(\theta +\frac{2\pi }{3}\right)}\hfill & \hfill {\displaystyle \sum _{h=1}^m{M}_{k{q}_h}cosh\left(\theta +\frac{2\pi }{3}\right)}\hfill & \hfill {\displaystyle \sum _{h=1}^m{M}_{k{D}_h}cosh\left(\theta +\frac{2\pi }{3}\right)}\hfill & \hfill -{\displaystyle \sum _{h=1}^m{M}_{k{Q}_h}cosh\left(\theta +\frac{2\pi }{3}\right)}\hfill \end{array}\right].$

Combining Eqs. 4-3 to 4-12 results in a unified representation for the electrical part of the synchronous machine having the form

$p\mathrm{\Psi }=v-R{L}^{-1}\mathrm{\Psi }.$

It is important to note that, for the computation of the state variables with Eq. 4-13, the inverse of the time-varying inductance matrix must be obtained at each step of integration.

The electric torque is expressed in terms of the stator currents and flux linkages as

$T_e=p\frac{2}{3\sqrt{3}}\left[{\mathrm{\Psi }}_a\left(i_b-i_c\right)+{\mathrm{\Psi }}_b\left(i_c-i_a\right)+{\mathrm{\Psi }}_c\left(i_a-i_b\right)\right]\text{,}$

where p is the number of poles.

4.1.2 Mechanical Equations of Synchronous Machine

The second-order mechanical equation of a synchronous machine can be decomposed into two first-order differential equations: one for the mechanical angular velocity of the rotor ω_r and the other for the mechanical rotor angle δ. The constant k_D is usually incorporated into the angular velocity equation to add a damping component that is proportional to the difference of angular velocities ω_r and ω_B:

$\frac{d{\omega }_r}{dt}=\frac{{\omega }_B}{2H}\left(T_m-T_e-k_D\left({\omega }_r-{\omega }_B\right)\right).$

$\frac{d\delta }{dt}={\omega }_r-{\omega }_B\text{,}$

where

$H=\frac{1}{2}·\frac{J{\omega }_B^2}{{\left(V,A\right)}_{\mathrm{base}}}.$

In the above equations ω_B is the rated angular velocity of the rotor, k_D is the damping factor (pu torque/pu angular velocity), H is the unit inertia constant (watt·s/VA at rated angular velocity), J is the axial combined (rotor and prime mover) moment of inertia (kg m²), and (VA)_base is the apparent power base S_base.

4.1.3 Magnetic Saturation of Synchronous Machine

This section introduces a simple approach to approximately include magnetic saturation in the synchronous machine equations [17]. The nonlinear effect of saturation in a synchronous machine is modeled according to the following algorithm, which is based on modifying the stator currents in dq0 coordinates.

• For the input stator currents and fluxes (e.g., i_a, i_b, i_c, and Ψ_a, Ψ_b, Ψ_c) apply the dq0 transformation to obtain i_d, i_q, i_o, and Ψ_d, Ψ_q, Ψ_o:

$\begin{array}{l}\left[\begin{array}{c}\hfill i_d\hfill \\ \hfill i_q\hfill \\ \hfill i_o\hfill \end{array}\right]=\left[T_{\mathrm{PARK}}\right]\left[\begin{array}{c}\hfill i_a\hfill \\ \hfill i_b\hfill \\ \hfill i_c\hfill \end{array}\right]\text{,}\\ \left[\begin{array}{c}\hfill {\mathrm{\Psi }}_d\hfill \\ \hfill {\mathrm{\Psi }}_q\hfill \\ \hfill {\mathrm{\Psi }}_o\hfill \end{array}\right]=\left[T_{\mathrm{PARK}}\right]\left[\begin{array}{c}\hfill {\mathrm{\Psi }}_a\hfill \\ \hfill {\mathrm{\Psi }}_b\hfill \\ \hfill {\mathrm{\Psi }}_c\hfill \end{array}\right]\end{array}$

where the Park transformation is

$\left[T_{\mathrm{PARK}}\right]=\sqrt{\frac{2}{3}}\left[\begin{array}{lll}cos\theta \hfill & cos\left(\theta -120°\right)\hfill & cos\left(\theta +120°\right)\hfill \\ -sin\theta \hfill & -sin\left(\theta -120°\right)\hfill & -sin\left(\theta +120°\right)\hfill \\ 1/\sqrt{2}\hfill & 1/\sqrt{2}\hfill & 1/\sqrt{2}\hfill \end{array}\right]$

• Calculate the dq-components of the total mmf in the machine as

$\begin{array}{cc}\hfill \begin{array}{l}{I}_d=i_d+i_f+{\displaystyle \sum _{j=1}^n{i}_{kdj}}\\ I_q=i_q+{\displaystyle \sum _{j=1}^n{i}_{kqj}}\end{array}\hfill & \hfill \text{,}\hfill \end{array}$

where kdj and kqj are the number of damper windings of d- and q-axes, respectively.

• For given saturation characteristics of the d- and q-axes, saturated mmfs (I_d′and I_q′) are calculated based on a polynomial approximation, for example,

$\begin{array}{cc}\hfill \begin{array}{l}{I}_d^{\prime }={\alpha }_d{\mathrm{\Psi }}_d+{\beta }_d{\mathrm{\Psi }}_d^n\\ I_q^{\prime }={\alpha }_q{\mathrm{\Psi }}_q+{\beta }_q{\mathrm{\Psi }}_q^m\end{array}\hfill & \hfill .\hfill \end{array}$

• The relationship between the saturated mmfs of Eq. 4-20 and linear mmfs of Eq. 4-19 are

$\begin{array}{cc}\hfill \begin{array}{l}{K}_d=I_d^{\prime }/I_d\\ K_q=I_q^{\prime }/I_q\end{array}\hfill & \hfill .\hfill \end{array}$

• Stator and rotor currents are now adjusted for saturation, as follows:

$\begin{array}{cc}\hfill \begin{array}{l}{i}_a^{\prime }=K_d{i}_a,i_b^{\prime }=K_d{i}_b,i_c^{\prime }=K_d{i}_c\\ i_f^{\prime }=K_d{i}_f\\ i_{kd}^{\prime }=K_d{i}_{kd},i_{kD}^{\prime }=K_d{i}_{kD}\\ i_{kq}^{\prime }=K_q{i}_{kq},i_{kQ}^{\prime }=K_q{i}_{kQ}\end{array}\hfill & \hfill .\hfill \end{array}$

4.1.4 Sinusoidal Model of a Synchronous Machine in dq0 Coordinates

Several reference frames can be employed to represent synchronous machine operation. The first and most widely used model is based on the concept of the ideal synchronous machine represented by fictitious dq0 coordinates attached to the rotating rotor reference frame [4,5], as shown in Fig. 4.1. This model assumes balanced operating conditions at the input terminals and within the machine. Synchronous machines can be also represented in αβ0 coordinates [10] to allow for a natural transition between abc and dq0 coordinates.

4.2.1 Definition of Transient and Subtransient Reactances as a Function of Leakage and Mutual Reactances

The dq0 model requires the availability of values for the synchronous (X_d, X_q), transient (X_d′, X_q′), and subtransient (X_d^″, X_q^″) reactances of synchronous machines. Most turbogenerators have field windings in the d-axis only and none in the q-axis, therefore $X_q^{\mathit{\prime }}\approx X_q$. The transient reactance X_d′ can be defined in terms of leakage and mutual reactances, as depicted in Fig. 4.12:

$X_d^{\prime }=X_{\mathit{al}}+\frac{X_{af}{X}_{\mathit{fl}}}{X_{af}+X_{\mathit{fl}}}\text{,}$

where X_al is the amature (stator) leakage reactance, X_fl is the field leakage reactance, and X_af is the mutual reactance between armature and field circuits.

Correspondingly, one obtains for the subtransient reactance X_d^″ (Fig. 4.13):

$X_d^{″}=X_{\mathit{al}}+\frac{X_{af}{X}_{\mathit{fl}}{X}_{\mathit{dl}}}{X_{af}{X}_{\mathit{fl}}+X_{af}{X}_{\mathit{dl}}+X_{\mathit{dl}}{X}_{\mathit{fl}}}\text{,}$

where X_dl is the d-axis damper winding leakage reactance.

Representative per-unit values for a typical turbogenerator are

$X_d=1.6\mathit{,}{X}_q=1.4\mathit{,}{X}_d^{\mathit{\prime }}=0.2\mathit{,}{X}_d^{\mathit{″}}=0.15.$

In general, 1 pu ≤ X_d ≤ 2 pu, 1 pu ≤ X_q ≤ 2 pu, 0.2 pu ≤ X_d′ ≤ 0.4 pu, 0.1 pu ≤ X_d^″ ≤ 0.3 pu, and the values of X_q′ and X_q^″ depend on the field and damper winding design within the q-axis, respectively. Note that the value of X_q^″ depends on the rotor construction and the damper winding associated with the q-axis: if there are no additional damper bars located on the rotor pole, then X_q^″ is relatively large and in the neighborhood of X_q. In the presence of damper windings in the q-axis X_q^″ is somewhat larger than X_d^″ because the damper winding (e.g., solid rotor or embedded damper bars on the rotor pole) of the q-axis is less effective than that of the d-axis. The rationale for selecting the above ranges for the various reactances lies in the stability requirements for generators when operating on the power system: machines with small reactances exhibit better stability than machines with large reactances; or in other words, machines with small reactances or inductances have smaller time constants than those with large reactances or inductances. Small reactances require a large air gap and a large field current for setting up the maximum flux density across the air gap of about B_max = 0.7 T. The large air gap makes machines less efficient as compared to those with small air gaps. One has to weigh the benefits of a more stable but less efficient machine versus that with less stability but greater efficiency. In addition, machines with small reactances result in larger short-circuit currents and larger transient torques and winding forces than machines with larger reactances.

4.2.2 Phasor Diagrams for Round-Rotor Synchronous Machines

There are two ways of drawing equivalent circuits and phasor diagrams of synchronous machines. The first one is based on the so-called consumer system, where the terminal current flows into the equivalent circuit, and the second one is the generator system, where the terminal current flows out of the equivalent circuit. The first one is mostly employed by engineers concerned with drives, and the latter one is mostly used by power system engineers who are concerned with generation issues.

4.2.2.1 Consumer (Motor) Reference Frame

Figure 4.14a depicts the equivalent circuit of a round-rotor synchronous machine based on the consumer (motor) reference current system. Figure 4.14b illustrates the corresponding phasor diagram for overexcited operation, and Fig.4.14c pertains to underexcited operation. Note that the polarity of the voltages is indicated by + and – signs as well as by arrows, where the head of the arrow coincides with the + sign and the tail of the arrow with the – sign. Such an arrow notation makes it easier to draw phasor diagrams. The phasor diagrams are not to scale because the ohmic voltage drop $\tilde{V}$_R is normally much smaller than the reactive voltage drop $\tilde{V}$_X.

4.2.2.2 Generator Reference Frame

Figure 4.15a depicts the equivalent circuit of a round-rotor synchronous machine based on the generator reference current system. Figure 4.15b,c illustrate the corresponding phasor diagram for overexcited and underexcited operation, respectively.

4.2.2.3 Similarities between Synchronous Machines and Pulse-Width-Modulated (PWM) Current-Controlled, Voltage-Source Inverters

Inverters are electronic devices transforming voltages and currents from a DC source to an equivalent AC source. Figure 4.16a illustrates the actual circuit of an inverter, where the input voltage is a DC voltage V_dc and the output voltage is an AC voltage ${\tilde{V}}_{\mathrm{load}}$. It is assumed that the PWM switching is lossless. In Fig. 4.16b the DC voltage (V_dc/2) is transformed to the AC side and represented by the phasor (${\tilde{V}}_{\mathit{dc}}$/2), which makes the equivalent circuit of Fig. 4.16b similar to that of a round-rotor synchronous machine, as depicted in Fig. 4.15a. The relation between the (fundamental) output voltage |${\tilde{V}}_{\mathrm{load}}$| of the inverter and the input voltage ${\tilde{V}}_{\mathit{dc}}$/2 (transformed to the AC side) is given [28] by

$\left|{\tilde{V}}_{\mathrm{load}}\right|=m\cdot \frac{\left|\left({\tilde{V}}_{\mathit{dc}}/2\right)\right|}{\sqrt{2}}$

  (4-26)

where m ≤ 1 is the modulation index of the (sinusoidal) PWM. This relation appears to hold for operation around unity displacement (fundamental power) factor only for m = 1 [29,30]. In these references it is shown that at lagging (overexcited, delivering reactive power to the grid) displacement power factor a higher input voltage V_dc than specified by Eq. 4-26 is required, whereas for leading (underexcited, absorbing reactive power from the grid) displacement power factor a smaller input voltage V_dc is sufficient. For example, although for unity displacement factor V_{dc_unity_pf} = 400 V is acceptable, a higher input voltage, e.g., V_{dc_lagging_pf} = 600 V is required for displacement factors larger than cos φ = 0.8 lagging (overexcited) [29,30] at |${\tilde{V}}_{\mathit{load}}$| = 139 V, where m = 0.66.

4.2.2.4 Phasor Diagram of a Salient-Pole Synchronous Machine

The d- and q-equivalent circuits and the associated phasor diagram of a (balanced) salient-pole synchronous machine are given in Fig. 4.17a,b,c. Note there is no zero-sequence equivalent circuit, which becomes important for unbalanced operation (e.g., asymmetrical short-circuits) of synchronous machines only. Figure 4.17c represents the phasor diagram without cross-coupling between the d- and q-axes due to saturation. The relation between voltages, currents, and reactances is given by the phasor diagram of Fig. 4.18 including cross-coupling of d- and q-axes parameters [20,23]. This cross-coupling is due to saturation of the machine and will be neglected in subsequent sections.

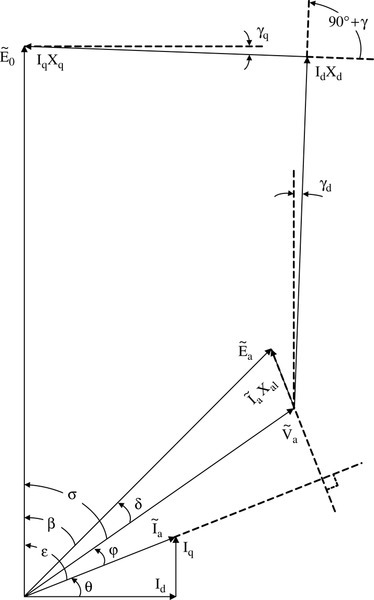
According to [7] the following relations are valid.

Terminal voltage component in d-axis as a function of the fluxes and currents in d- and q-axes:

$V_d=-{\mathrm{\Psi }}_q\mathit{–}{R}_a{I}_d=X_q{I}_q\mathit{–}{R}_a{I}_d.$

  (4-27)

Terminal voltage component in q-axis:

$V_q={\mathrm{\Psi }}_d\mathit{–}{R}_a{I}_q=E_a\mathit{–}{X}_d{I}_d\mathit{–}{R}_a{I}_q.$

  (4-28)

Eqs. 4-27 and 4-28 solved for I_d and I_q yield

$I_d=\frac{-R_a{V}_d+X_q\left(E_a-V_q\right)}{X_d{X}_q+R_a^2}\text{,}$

  (4-29)

$I_q=\frac{X_a{V}_d+R_a\left(E_a-V_q\right)}{X_d{X}_q+R_a^2}\text{,}$

  (4-30)

which may be written in terms of the terminal voltage ${\tilde{V}}_a$:

$I_d=\frac{-R_a\left|{\tilde{V}}_a\right|sin\delta +X_q\left(E_a-\left|{\tilde{V}}_a\right|cos\delta \right)}{X_d{X}_q+R_a^2}\text{,}$

  (4-31)

$I_q=\frac{X_d\left|{\tilde{V}}_a\right|sin\delta +R_a\left(E_a-\left|{\tilde{V}}_a\right|cos\delta \right)}{X_d{X}_q+R_a^2}\text{,}$

  (4-32)

where

$\left|{\tilde{V}}_a\right|=\sqrt{V_d^2+V_q^2}\text{,}$

  (4-33)

$\left|{\tilde{I}}_a\right|=\sqrt{I_d^2+I_q^2}.$

  (4-34)

4.2.3 Application Example 4.1: Steady-State Analysis of a Nonsalient-Pole (Round-Rotor) Synchronous Machine

A three-phase (m = 3), four-pole (p = 4) nonsalientpole (round-rotor) synchronous machine has the parameters X_S = 2 pu and R_a = 0.05 pu. It is operated at (the phase voltage) V_a = 1 pu at an overexcited (lagging current based on the generator reference system, where the current flows out of the machine) displacement power factor of cos φ = 0.8 lagging, and per-phase current $\left|{\tilde{I}}_a\right|$ = 1 pu. The base (rated phase) values are $\left|{\tilde{V}}_a\right|{}_{\mathrm{rated}}$ = V_base = 24 kV, $\left|{\tilde{I}}_a\right|{}_{\mathrm{rated}}$ = I_base = 1.4 kA, and the base impedance is Z_base = V_base/I_base = 17.14 Ω.

a) Draw the per-phase equivalent circuit of this machine.

b) What is the total rated apparent input power S (expressed in MVA)?

c) What is the total rated real input power P (expressed in MW)?

d) Draw a per-phase phasor diagram with the voltage scale of 1.0 pu ≡ 3 inches, and the current scale of 1.0 pu ≡ 2.5 inches.

e) From this phasor diagram determine the per-phase induced voltage |Ẽ_a| and the torque angle δ.

f) Calculate the rated speed (in rpm) of this machine at f = 60 Hz.

g) Calculate the angular velocity ω_S (in rad/s).

h) Calculate the total (approximate) shaft power P_shaft ≈ 3(E_a · V_a · sin δ)/X_S.

i) Find the shaft torque T_shaft (in Nm).

j) Determine the total ohmic loss of the motor $P_{\mathit{loss}}=3\cdot R_a{\left|{\tilde{I}}_a\right|}^2$.

k) Repeat the above analysis for cos φ = 0.8 underexcited (leading current based on generator notation) displacement power factor and $\left|{\tilde{I}}_a\right|$ = 0.5 pu.

Solution to Application Example 4.1

a) The per-phase equivalent circuit of a nonsalient-pole synchronous machine based on generator notation is shown in Fig. 4.15a. The parameters of the machine are in ohms: $R_a=0.05·Z_{\mathrm{base}}=\left(0.05\right)\left(17.14\mathrm{\Omega }\right)=0.857\mathrm{\Omega },\mathrm{and}{X}_S=2·Z_{\mathrm{base}}=2\left(17.14\mathrm{\Omega }\right)=34.28\mathrm{\Omega }.$

b) $S_{\mathrm{rated}}=3·{V_{\mathrm{a}\_}}_{\mathrm{rated}}·{I_{\mathrm{a}\_}}_{\mathrm{rated}}=3\left(24\mathrm{kV}\right)\left(1.4\mathrm{k}\mathrm{A}\right)=100.8\mathrm{M}\mathrm{V}\mathrm{A}.$ (E4.1-1)

c) $P_{\mathrm{rated}}=S_{\mathrm{rated}}\cdot cos\mathrm{\phi }=80.64\mathrm{M}\mathrm{W}.$ (E4.1-2)

d) The phasor diagram is given in Fig. E4.1.1.

$\begin{array}{l}\phi ={cos}^{-1}\left(0.8\right)=0.6435\mathrm{rad}\mathrm{or}36.87°\mathrm{lagging}\end{array}$

$\left|{\tilde{V}}_{\mathrm{a}-\mathrm{rated}}\right|$ = 1 pu = 24 kV ≡ 3 inches,
$\left|{\tilde{I}}_{\mathrm{a}-\mathrm{rated}}\right|$ = 1 pu = 1.4 kA ≡ 2.5 inches,
$\left|{\tilde{I}}_{\mathrm{a}-\mathrm{rated}}\right|$ · R_a = 1.4kA(0.05)(17.141 Ω) = 1199.8 V ≡ 0.15 inches,
$\left|{\tilde{I}}_{\mathrm{a}-\mathrm{rated}}\right|$ · X_s = 1.4 kA(2)(17.141 Ω) = 47992 V ≡ 6 inches.

e) For the induced voltage one obtains

$E_a=\sqrt{\begin{array}{l}{\left(\left|{\tilde{V}}_a\right|+\left|{\tilde{V}}_R\right|cos\phi +\left|{\tilde{V}}_X\right|sin\phi \right)}^2\\ +{\left(\left|{\tilde{V}}_X\right|cos\phi -\left|{\tilde{V}}_R\right|sin\phi \right)}^2\end{array}}=2.735\mathrm{p}\mathrm{u},$

where
$\left|{\tilde{V}}_a\right|=1\mathrm{p}\mathrm{u},\left|{\tilde{V}}_X\right|=2\mathrm{p}\mathrm{u},\left|{\tilde{V}}_R\right|$ = 0.05 pu, sin φ = 0.6, and cos φ = 0.8.
The torque angle δ is

$\begin{array}{l}\delta ={cos}^{-1}\left\{\left(\left|{\tilde{V}}_a\right|+\left|{\tilde{V}}_R\right|cos\phi +\left|{\tilde{V}}_X\right|sin\phi \right)/E_a\right\}=0.611\mathrm{rad}\mathrm{or}35°.\end{array}$

f) Rated speed is

${\mathit{n}}_{\mathit{S}}=120\mathrm{f}/\mathrm{p}=120\left(60\right)/4=1800\mathrm{rpm}.$

g) Angular velocity is

${\omega }_S=2\pi n_S/60=188.7\mathrm{rad}/\mathrm{s}.$

h) Approximate shaft power is

${\mathit{P}}_{\mathrm{shaft}}\approx 3\left({\mathit{E}}_a·{\mathit{V}}_a·sin\delta \right)/{\mathit{X}}_{\mathit{S}}=3\left[\left(2.735\right)\left(24\mathrm{k}\right)\left(24\mathrm{k}\right)sin\left(0.611\mathrm{rad}\right)\right]/\left[\left(2\right)\left(17.14\right)\right]=79.1\mathrm{M}\mathrm{W}.$

i) The shaft torque T_shaft is

$T_{\mathrm{shaft}}=P_{\mathrm{shaft}}/{\omega }_S=419.14\mathrm{k}\mathrm{N}\mathrm{m}.$

j) The total ohmic loss of the motor is

$P_{\mathrm{loss}}=3\cdot R_a\left|{\tilde{I}}_{\mathrm{a}}\right|{}^2=3\left(0.05\right)\left(17.14\right){\left(1.4\mathrm{k}\right)}^2=5.04\mathrm{M}\mathrm{W}.$

k) Repeat the above analysis for underexcited (leading current based on generator reference system) displacement power factor cos φ = 0.8 leading and $\left|{\tilde{I}}_a\right|$ = 0.5 pu.

a) see Fig. 4.15a

b) S_rated = 3 · V_{a_rated} · I_{a_rated} = 3(24 kV)(0.7kA) = 50.4 MVA.

c) P_rated = S_rated · cos φ = 40.32 MW.

d) The phasor diagram is given in Fig. E4.1.2.

$\begin{array}{l}\phi ={cos}^{–1}\left(0.8\right)=0.6435\mathrm{rador}36.87°\mathrm{leading}\left(\mathrm{underexcited}\right),\\ \left|{\tilde{V}}_{\mathrm{a}-\mathrm{rated}}\right|=1\mathrm{p}\mathrm{u}=24\mathrm{kV}\text{≡}3\mathrm{inches},\\ \left|{\tilde{I}}_{\mathrm{a}-\mathrm{rated}}\right|=0.5\mathrm{p}\mathrm{u}=700\mathrm{A}\text{≡}1.25\mathrm{inches},\\ \left|{\tilde{I}}_{\mathrm{a}-\mathrm{rated}}\right|·R_a=700\mathrm{A}\left(0.05\right)\left(17.141\mathrm{\Omega }\right)=599.9\mathrm{V}\text{≡}0.075\mathrm{inches},\\ \left|{\tilde{I}}_{\mathrm{a}-\mathrm{rated}}\right|·X_S=700\mathrm{A}\left(2\right)\left(17.14\mathrm{\Omega }\right)=23.996\mathrm{kV}\text{≡}3\mathrm{inches}.\end{array}$

e) For the induced voltage one obtains

$\begin{array}{c}{E}_a=\sqrt{\begin{array}{l}{\left(\left|{\tilde{V}}_a\right|+\left|{\tilde{V}}_R\right|cos\phi -\left|{\tilde{V}}_X\right|sin\phi \right)}^2\\ +{\left(\left|{\tilde{V}}_X\right|cos\phi +\left|{\tilde{V}}_R\right|sin\phi \right)}^2\end{array}}\\ =0.917\mathrm{p}\mathrm{u}\mathrm{or}22.004\mathrm{k}\mathrm{V}\text{,}\hfill \end{array}$

where
$\left|{\tilde{V}}_a\right|$ = 1 pu, $\left|{\tilde{V}}_X\right|$ = 1 pu, $\left|{\tilde{V}}_r\right|$ = 0.025 pu, sin φ = 0.6, cos φ = 0.8.
The torque angle δ is

$\delta ={cos}^{-1}\left\{\left(\left|{\tilde{V}}_a\right|+|{\tilde{V}}_{R}cos\phi -|{\tilde{V}}_X|sin\phi \right)|/E_a\right\}=1.095\mathrm{rad}\mathrm{or}62.74°.$

f) Rated speed is

$n_S=120\mathrm{f}/\mathrm{p}=120·60/4=1800\mathrm{rpm}.$

g) Angular velocity is ω_S = 2πn_S/60 = 188.7 rad/s.

h) Approximate shaft power is

$P_{\mathrm{shaft}}\approx 3\left(E_a·V_a·sin\delta \right)/X_S=3\left[\left(0.917\right)\left(24\mathrm{k}\right)\left(24\mathrm{k}\right)sin\left(1.095\mathrm{rad}\right)\right]/\left[\left(2\right)\left(17.14\right)\right]=41.09\mathrm{M}\mathrm{W}.$

i) The shaft torque T_shaft is T_shaft = P_shaft/ω_S = 217.75 kNm.

j) The total ohmic loss of the motor is

$P_{\mathrm{loss}}=3·R_a\left|{\tilde{I}}_a\right|{}^2=3\left(0.05\right)\left(17.14\right){\left(0.7\mathrm{k}\right)}^2=1.26\mathrm{M}\mathrm{W}.$

4.2.4 Application Example 4.2: Calculation of the Synchronous Reactance X_S of a Cylindrical-Rotor (Round-Rotor, Nonsalient-Pole) Synchronous Machine

A p = 2 pole, f = 60 Hz synchronous machine (generator, alternator, motor) is rated S_rat = 16 MVA at a lagging (generating reference system) displacement power factor cos φ = 0.8, a line-to-line terminal voltage of V_L-L = 13,800 V, and a (one-sided) air-gap length of g = 0.0127 m. The stator has 48 slots and has a three-phase double-layer, 60° phase-belt winding with 48 armature coils having a short pitch of 2/3. Each coil consists of one turn N_coil = 1. Sixteen stator coils are connected in series, that is, the number of series turns per phase of the stator (st) are N_{st phase} = 16 (see Fig. E4.2.1). The maximum air-gap flux density at no load (stator current I_{st phase} = 0) is B_{st max} = 1 T.

There are eight field coils per pole (see Fig. E4.2.2) and they are pitched 44-60-76-92-124-140-156-172 degrees, respectively, as indicated in Fig. E4.2.2. Each field coil has 18 turns. The developed rotor (field) magnetomotive force (mmf) F_r is depicted in Fig. E4.2.3. Note that the field mmf is approximately sinusoidal.

a) Calculate the distribution (breadth) factor of the stator winding k_stb (= k_std).

b) Calculate the fundamental pitch factor of the stator winding k_stp1.

c) Calculate the pitch factor of the rotor (r) winding k_rp.

d) Determine the stator flux Φ_stmax.

e) Compute the area (area_p) of one pole.

f) Compute the field (f) current I_fo required at no load.

g) Determine the synchronous (s) reactance (per phase value) X_S of this synchronous machine in ohms.

h) Find the base impedance Z_base expressed in ohms.

i) Express the synchronous reactance X_S in per unit (pu).

Solution to Application Example 4.2

a) Calculation of the distribution (breadth) factor of the stator winding k_stb = k_std is as follows. The breadth factor is defined for one phase belt as

$k_{stb}=\frac{\mathrm{geometric}\mathrm{sum}{\displaystyle \sum _{i=1}^8{F}_i}}{\mathrm{algebraic}\mathrm{sum}{\displaystyle \sum _{i=1}^8{F}_i}}.$

It is convenient to evaluate Eq. E4.2-1 graphically, as shown in Fig. E4.2.4. Note that one slot pitch corresponds to 360°/48 = 7.5°. Thus, one gets from Fig. E4.2.4 the distribution or breadth factor

$k_{stb}=0.96.$

b) Calculation of the pitch factor of the stator winding k_stp1 is as follows. One stator turn spans 16 slots out of 24 slots, that is, it has a pitch of (2/3); therefore, one obtains for the fundamental n = 1

$k_{\mathit{stp}1}=\left|sin\left(\frac{n\beta }{2}\right)\right|=\left|sin\left(\frac{\left(1\right)\left(120\right)}{2}\right)\right|=0.866$

or for the 5th harmonic n = 5

$k_{\mathit{stp}5}=\left|sin\left(\frac{\left(5\right)\left(120\right)}{2}\right)\right|=0.866.$

The 5th harmonic is not attenuated; therefore, the choice of a 2/3 winding pitch is not recommended.
The total fundamental winding factor of the stator winding is now

$k_{st}=k_{stb}·k_{\mathit{stp}1}=0.96\left(0.866\right)=0.831.$

c) Calculate the pitch factor of the rotor (r) winding k_rp as follows. The fundamental (n = 1) pitch-factor of the rotor winding is correspondingly

$k_{rp}=\left\{\left|{\displaystyle \sum _{i=1}^{8}sin\left(\frac{n{\beta }_i}{2}\right)}\right|\right\}/8\text{,}$

$\begin{array}{c}{k}_{rp}=\left\{\left|sin\left(\frac{44°}{2}\right)\right|+\left|sin\left(\frac{60°}{2}\right)\right|+\left|sin\left(\frac{76°}{2}\right)\right|+\left|sin\left(\frac{92°}{2}\right)\right|+\left|sin\left(\frac{124°}{2}\right)\right|\right.\\ \left.+\left|sin\left(\frac{140°}{2}\right)\right|+\left|sin\left(\frac{156°}{2}\right)\right|+\left|sin\left(\frac{172°}{2}\right)\right|\right\}/8\Rightarrow k_{rp}=0.751.\end{array}$

d) Determination of the stator flux Φ_stmax is as follows. The induced voltage in the stator winding per phase is

$E_{\mathit{ph}}=4.44\cdot f\cdot N_{\mathit{stph}}\cdot k_{stb}\cdot k_{\mathit{stp}1}\cdot {\mathrm{\Phi }}_{\mathrm{stmax}}$

or one obtains for the stator flux

${\mathrm{\Phi }}_{st\max }=\frac{E_{L-L}}{\sqrt{3}\cdot 4.44\cdot f\cdot N_{\mathit{stph}}\cdot k_{stb}\cdot k_{\mathit{stp}1}}$

with E_L-L = V_L-L = 13,800 V at no load, one gets the flux for no-load condition:

${\mathrm{\Phi }}_{\mathit{st}\max }^{\mathrm{no}-\mathrm{load}}=\frac{13800}{\sqrt{3}\left(4.44\right)\left(60\right)\left(16\right)\left(0.96\right)\left(0.866\right)}=2.25\frac{\mathrm{Wb}}{\mathrm{pole}}.$

e) Compute the area (area_p) of one pole:

${\mathrm{area}}_p=\frac{{\mathrm{\Phi }}_{st\max }^{\mathrm{no}-\mathrm{load}}}{B_{\text{max}}}=2.25{\mathrm{m}}^2.$

f) Compute the field (f) current I_fo required at no load:

$\begin{array}{c}{I}_{fo}=\frac{B_{st\max }\cdot p\cdot g\cdot \pi }{4\cdot {\mu }_0\cdot k_{rp}\cdot N_{\mathit{rtot}}}=\frac{1\left(2\right)\left(0.0127\right)\left(\pi \right)}{4\left(4\pi \times {10}^{-7}\right)\left(0.751\right)\left(288\right)}=73.4A.\end{array}$

g) Determine the synchronous (s) reactance (per phase value) X_S in ohms. The self-inductance of phase a is

$\begin{array}{c}{L}_{\mathit{aa}}=\frac{{\lambda }_{\mathit{aa}}}{i_a}=\frac{N_{st}\cdot {\mathrm{\phi }}_{st\max }}{i_a}=\frac{N_{st}\cdot B_{st\max }\cdot {\mathrm{area}}_p}{i_a}\\ =\frac{{\mu }_0\cdot 4\cdot k_{stb}\cdot k_{\mathit{stp}1}\cdot {\left({\mathrm{N}}_{\mathrm{stph}}\right)}^2\cdot {\mathrm{area}}_p}{p\cdot g\cdot \pi }\end{array}$

$\begin{array}{l}{L}_{\mathit{aa}}=\frac{4\pi \times {10}^{-7}\left(4\right)\left(0.96\right)\left(0.866\right){\left(16\right)}^2\left(2.25\right)}{2\left(0.0127\right)\left(\pi \right)}=30.16\mathrm{mH}.\end{array}$

According to Concordia [7]

$L_d=L_{\mathit{aa}}+L_{\mathit{ab}}+1.5L_{\mathit{aa}2}.$

Neglecting L_aa2 and L_aa ≈ L_ab one gets for the synchronous inductance L_d

$L_d\approx 2\cdot L_{\mathit{aa}}=60.33\mathrm{mH}.$

The synchronous reactance of the round-rotor machine is

$X_S=\omega L_d=\omega L_S=22.74\mathrm{\Omega }.$

The base voltage is

$V_{\mathrm{base}}=\frac{V_{L-L}}{\sqrt{3}}=V_{\mathrm{phase}}=7,967\mathrm{V}.$

The base apparent power is per phase

$S_{\mathrm{base}}=S_{\mathrm{phase}}=\frac{S_{\mathrm{rat}}}{3}=5.33\mathrm{M}\mathrm{V}\mathrm{A}$

and the base current is

$I_{\mathrm{base}}=I_{\mathrm{phase}}=\frac{S_{\mathrm{base}}}{V_{\mathrm{base}}}=669\mathrm{A}.$

h) Find the base impedance Z_base expressed in ohms. The base impedance becomes

$Z_{\mathrm{base}}=\frac{V_{\mathrm{base}}}{I_{\mathrm{base}}}=11.9\mathrm{\Omega }.$

i) Express the synchronous reactance X_S in per unit (pu). The per-unit synchronous reactance is now

$X_S^{pu}=\frac{X_S}{Z_{\mathrm{base}}}=\frac{22.74}{11.9}=1.91\mathrm{p}\mathrm{u}.$

4.2.5 Application Example 4.3: dq0 Modeling of a Salient-Pole Synchronous Machine

Engineers are most concerned about the torques generated by the machine under abnormal operating conditions such as:

• balanced three-phase short-circuit,

• line-to-line short-circuit,

• line-to-neutral short-circuit,

• out-of-phase synchronization,

• synchronizing and damping torques,

• reclosing, and

• stability.

Linear (not saturation-dependent) reactances are assumed and amortisseur (damper) windings are neglected except for some out-of-phase synchronization results and for reclosing events. Most machines have very weak damper windings and, therefore, this assumption is justified. Synchronizing T_S and damping T_D torques of the salient-pole synchronous machine using dq0 modeling are also addressed in Problem 4.8.

Solution to Application Example 4.3

a) Balanced Three-Phase Short-Circuit. If the terminals of a synchronous generator are short circuited at rated no-load excitation one obtains the balanced short-circuit currents in per unit [31]:

$\begin{array}{l}{i}_a\left(\phi \right)=\frac{1}{X_d}cos\left(\phi +\alpha \right)+\frac{\left(X_d-X_d^{\prime }\right)}{X_d{X}_d^{\prime }}{e}^{-\phi /T_d^{\prime }}cos\left(\phi +\alpha \right)\\ -\frac{1}{2}\left(\frac{1}{X_d^{\prime }}+\frac{1}{X_q}\right)e^{-\phi /Ta}cos\alpha -\frac{1}{2}\left(\frac{1}{X_d^{\prime }}+\frac{1}{X_q}\right)e^{-\phi /Ta}·\\ cos\left(2\phi +\alpha \right)\end{array}$

$\begin{array}{l}{i}_b\left(\phi \right)=\frac{1}{X_d}cos\left(\phi +\alpha -120°\right)+\frac{\left(X_d-X_d^{\prime }\right)}{X_d{X}_d^{\prime }}{e}^{-\phi /T_d^{\prime }}·\\ cos\left(\phi +\alpha -120°\right)+\frac{1}{4}\left(\frac{1}{X_d^{\prime }}+\frac{1}{X_q}\right)e^{-\phi /Ta}cos\alpha \\ +\frac{1}{2}\left(\frac{1}{X_d^{\prime }}-\frac{1}{X_q}\right)e^{-\phi /Ta}cos\left(2\phi +\alpha +\delta \right)\end{array}$

$\begin{array}{l}{i}_c\left(\phi \right)=\frac{1}{X_d}cos\left(\phi +\alpha +120°\right)+\frac{\left(X_d-X_d^{\prime }\right)}{X_d{X}_d^{\prime }}{e}^{-\phi /T_d^{\prime }}·\\ cos\left(\phi +\alpha +120°\right)+\frac{1}{4}\left(\frac{1}{X_d^{\prime }}+\frac{1}{X_q}\right)e^{-\phi /Ta}·\\ cos\alpha +\frac{1}{2}\left(\frac{1}{X_d^{\prime }}-\frac{1}{X_q}\right)e^{-\phi /Ta}cos\left(2\phi +\alpha -\delta \right)\text{,}\end{array}$

where tan δ = $\sqrt{3}$, φ = ωt.
The field current is

$i_f\left(\phi \right)=1+\frac{\left(X_d-X_d^{\prime }\right)}{X_d^{\prime }}\left(e^{-\phi /T^{\prime }\mathit{do}}-cos\phi e^{-\phi /Ta}\right)$

and the torque is

$T_{3-\mathrm{phase}}=\frac{\left(X_d^{\prime }-X_q\right)}{2X_d^{\prime }{X}_q}\cdot sin\left(2\phi \right)+\frac{1}{X_d^{\prime }}sin\phi .$

The maximum torque occurs at the angle φ_max which can be obtained from

$cos{\phi }_{\text{max}}=\frac{1}{4}\left(\frac{X_q}{X_q-X_d^{\prime }}\pm \sqrt{{\left(\frac{X_q}{\left(X_d^{\prime }-X_q\right)}\right)}^2+8}\right).$

Figure E4.3.1 illustrates the torque of Eqs. E4.3-5 and E4.3-6.

b) Line-to-Line Short-Circuit. The short-circuit of the two terminals b and c of a synchronous generator results in the line-to-line short-circuit current [31]

$i_b=\frac{\sqrt{3}\left(cos\phi -cos{\phi }_o\right)}{\left(X_q+X_d^{\prime }\right)-\left(X_q-X_d^{\prime }\right)cos2\phi }$

or for φ_o = 0

$i_b=\frac{\sqrt{3}\left(cos\phi -1\right)}{\left(X_q+X_d^{\prime }\right)-\left(X_q-X_d^{\prime }\right)cos2\phi }$

and the torque is

$T_{L-L}=-\frac{2}{\sqrt{3}}\left(sin\phi \right)i_b+\frac{2}{3}sin2\phi \left(X_d^{\prime }-X_q\right)i_b^2$

or

$\begin{array}{c}{T}_{L-L}=\frac{-2sin\phi \left(cos\phi -1\right)}{\left[\left(X_q+X_d^{\prime }\right)-\left(X_q-X_d^{\prime }\right)cos2\phi \right]}\\ +\frac{2sin2\phi \left(X_d^{\prime }-X_q\right){\left(cos\phi -1\right)}^2}{{\left[\left(X_q+X_d^{\prime }\right)-\left(X_q-X_d^{\prime }\right)cos2\phi \right]}^2}.\end{array}$

Figure E4.3.2 illustrates the torques of Eqs. E4.3-5, E4.3-6, and E4.3-10.

The open-circuit voltage induced in phase a in case of a short-circuit of line b with line c is

$e_a=-cos\phi -b\left(\begin{array}{l}\frac{\left[-sin\phi sin2\phi +\left(cos\phi -cos{\phi }_o\right)2cos2\phi \right]}{\left[a-bcos2\phi \right]}-\\ \frac{\left(cos\phi -cos{\phi }_o\right){\left(sin2\phi \right)}^{2}2b}{{\left[a-bcos2\phi \right]}^2}\end{array}\right)\text{,}$

where

$a=\left(X_q+X_d^{\prime }\right)\mathrm{and}b=\left(X_q-X_d^{\prime }\right).$

The maximum value of e_a occurs for φ_o = 0
Figure E4.3.3 illustrates the induced voltage e_a of Eqs. E4.3-11 and E4.3-12a,b.

c) Line-to-Neutral Short-Circuit. The current when phase a of a synchronous machine at no load is short-circuited is for θ = 90° + φ [31]

$i_a=\frac{3\left(cos\theta -cos{\theta }_o\right)}{\left(X_q-X_d^{\prime }\right)}\cdot \frac{1}{\frac{\left(X_d^{\prime }+X_q+X_o\right)}{\left(X_q-X_d^{\prime }\right)}-cos2\theta }$

or in terms of an infinite series

$\begin{array}{c}{i}_a=\frac{3\left(cos\theta -cos{\theta }_o\right)}{\left(X_q-X_d^{\prime }\right)}.\\ \frac{2a}{1-a^2}\left(1+2acos2\theta +2a^{2}cos4\theta +\dots \right)\text{,}\end{array}$

where

$a=\frac{\sqrt{X_q+\frac{X_o}{2}}-\sqrt{X_d^{\prime }+\frac{X_o}{2}}}{\sqrt{X_q+\frac{X_o}{2}}+\sqrt{X_d^{\prime }+\frac{X_o}{2}}}.$

Note that i_a must be initially zero, that is, φ = φ_o = 0 or θ_o = 90°.
The fundamental component becomes now

$i_{a1}=\frac{3cos\theta }{X_d^{\prime }+\sqrt{X_q+\frac{X_o}{2}}\cdot \sqrt{X_d^{\prime }+\frac{X_o}{2}}+\frac{X_o}{2}}$

or in terms of symmetrical components

$i_{a1}=\frac{3cos\theta }{X_d^{\prime }+X_2+X_o}.$

d) Out-of-Phase Synchronization. When synchronizing a generator (either machine or inverter) with the power system the following conditions must be met:

• phase sequence must be the same,

• the phase angle between the two voltage systems must be sufficiently small, and

• the slip must be small.

Synchronizing out of phase is an important issue because it generates the highest torques and forces (in particular within the end winding of a machine) when paralleled with the power system [31]. The torque during out-of-phase synchronization is as a function of time φ = ωt and the angle δ between the power system’s voltage and that of the synchronous machine voltage at the time of paralleling:

$\begin{array}{c}{T}_{\mathrm{out}-\mathrm{of}-\mathrm{phase}}=\frac{1}{X_q}\left[sin\delta \left(1-cos\phi \right)+\left(1-cos\delta \right)sin\phi \right]·\\ \left\{1+\frac{\left(X_q-X_d^{\prime }\right)}{X_d^{\prime }}\left[\left(1-cos\delta \right)\left(1-cos\phi \right)-sin\delta sin\phi )\right]\right\}.\end{array}$