CHAPTER 3
SET THEORY
3.1 SETS AND ELEMENTS
The development of logic that resulted in the work of Chapters 1 and 2 went through many stages and benefited from the work of various mathematicians and logicians through the centuries. Although modern logic can trace its roots to Descartes with his mathesis universalis and Gottfried Leibniz's De Arte Combinatoria (1666), the beginnings of modern symbolic logic is generally attributed to Augustus De Morgan [Formal Logic (1847)], George Boole [Mathematical Analysis of Logic (1847) and An Investigation of the Laws of Thought (1847)], and Frege [Begriffsschrift (1879), Die Grundlagen der Arithmetik (1884), and Grundgesetze der Arithmetik (1893)]. However, when it comes to set theory, it was Georg Cantor who, with his first paper, “Ueber eine Eigenschaft des Inbegriffs aller reellen algebraischen Zahlen” (1874), and over a decade of research, is the founder of the subject. For the next four chapters, Cantor's set theory will be our focus.
A set is a collection of objects known as elements. An element can be almost anything, such as numbers, functions, or lines. A set is a single object that can contain many elements. Think of it as a box with things inside. The box is the set, and the things are the elements. We use uppercase letters to label sets, and elements will usually be represented by lowercase letters. The symbol ∈ (fashioned after the Greek letter epsilon) is used to mean “element of,” so if A is a set and a is an element of A, write ∈ aA or, the more standard, a ∈ A. The notation a, b ∈ A means a ∈ A and b ∈ A. If c is not an element of A, write c ∉ A. If A contains no elements, it is the empty set. It is represented by the symbol ∅. Think of the empty set as a box with no things inside.
Rosters
Since the elements are those that distinguish one set from another, one method that is used to write a set is to list its elements and surround them with braces. This is called the roster method of writing a set, and the list is known as a roster. The braces signify that a set has been defined. For example, the set of all integers between 1 and 10 inclusive is
![]()
Read this as “the set containing 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.” The set of all integers between 1 and 10 exclusive is
![]()
If the roster is too long, use ellipses (...). When there is a pattern to the elements of the set, write down enough members so that the pattern is clear. Then use the ellipses to represent the continuing pattern. For example, the set of all integers inclusively between 1 and 1,000,000 can be written as
![]()
Follow this strategy to write infinite sets as rosters. For instance, the set of even integers can be written as
![]()
![]() EXAMPLE 3.1.1
EXAMPLE 3.1.1
- As a roster, { } denotes the empty set. Warning: Never write {∅} for the empty set. This set has one element in it.
- A set that contains exactly one element is called a singleton. Hence, the sets {1}, {f}, and {∅} are singletons written in roster form. Also, 1 ∈ {1}, f ∈ {f}, and ∅ ∈ {∅}.
- The set of linear functions that intersect the origin with an integer slope can be written as:

(Note: Here 0 represents the function f(x) = 0.)
Let A and B be sets. These are equal if they contain exactly the same elements. The notation for this is A = B. What this means is if any element is in A, it is also in B, and conversely, if an element is in B, it is in A. To fully understand set equality, consider again the analogy between sets and boxes. Suppose that we have a box containing a carrot and a rabbit. We could describe it with the phrase the box that contains the carrot and the rabbit. Alternately, it could be referred to as the box that contains the orange vegetable and the furry, cotton-tailed animal with long ears. Although these are different descriptions, they do not refer to different boxes. Similarly, the set {1, 3} and the set containing the solutions of (x − 1)(x − 3) = 0 are equal because they contain the same elements. Furthermore, the order in which the elements are listed does not matter. The box can just as easily be described as the box with the rabbit and the carrot. Likewise, {1, 3} = {3, 1}. Lastly, suppose that the box is described as containing the carrot, the rabbit, and the carrot, forgetting that the carrot had already been mentioned. This should not be confusing, for one understands that such mistakes are possible. It is similar with sets. A repeated element does not add to the set. Hence, {1, 3} = {1, 3, 1}.
Famous Sets
Although sets can contain many different types of elements, numbers are probably the most common for mathematics. For this reason particular important sets of numbers have been given their own symbols.

As rosters,
![]()
and
![]()
Notice that we define the set of natural numbers to include zero and do not make a distinction between counting numbers and whole numbers. Instead, write
![]()
and
![]()
![]() EXAMPLE 3.1.2
EXAMPLE 3.1.2
- 10 ∈ Z+, but 0 ∉ Z+.
- 4 ∈ N, but −5 ∉ N.
- −5 ∈ Z, but .65 ∉ Z.
- .65 ∈ Q and 1/2 ∈ Q, but π ∉ Q.
- π ∈ R, but 3 − 2i ∉ R.
- 3 − 2i ∈ C.
Of the sets mentioned above, the real numbers are probably the most familiar. It is the set of numbers most frequently used in calculus and is often represented by a number line. The line can be subdivided into intervals. Given two endpoints, an interval includes all real numbers between the endpoints and possibly the endpoints themselves. Interval notation is used to name these sets. A parenthesis next to an endpoint means that the endpoint is not included in the set, while a bracket means that the endpoint is included. If the endpoints are included, the interval is closed. If they are excluded, the interval is open. If one endpoint is included and the other is not, the interval is half-open. If the interval has only one endpoint, then the set is called a ray and is defined using the infinity symbol (∞), with or without the negative sign.
![]() DEFINITION 3.1.3
DEFINITION 3.1.3
Let a, b ∈ R such that a < b.

![]() EXAMPLE 3.1.4
EXAMPLE 3.1.4
We can describe (4, 7) as
the interval of real numbers between 4 and 7 exclusive
and [4, 7] as
all real numbers between 4 and 7 inclusive.
There is not a straightforward way to name the half-open intervals. For (4, 7], we can try
the set of all real numbers x such that 4 < x ≤ 7
or
the set of all real numbers greater than 4 and less than or equal to 7.
The infinity symbol does not represent a real number, so a parenthesis must be used with it. Furthermore, the interval (−∞, ∞) can be used to denote R.
Figure 3.1 A half-open interval and a closed ray.
![]() EXAMPLE 3.1.5
EXAMPLE 3.1.5
The interval (−1, 3] contains all real numbers that are greater than −1 but less than or equal to 3 [Figure 3.1(a)]. A common mistake is to equate (−1, 3] with {0, 1, 2, 3}. It is important to remember that (−1, 3] includes all real numbers between −1 and 3. Hence, this set is infinite, as is (−∞, 2). It contains all real numbers less than 2 [Figure 3.1(b)].
![]() EXAMPLE 3.1.6
EXAMPLE 3.1.6
Let p(x) := x + 2 = 7. Since p(5) and there is no other real number a such that p(a), there exists a unique x ∈ R such that p(x). However, if a is an element of Z− or (−∞, 5), then ¬p(a).
![]() EXAMPLE 3.1.7
EXAMPLE 3.1.7
If q(x) := x ≥ 10, then q(x) for all x ∈ [20, 100], there exists x ∈ Q such that ¬q(x), and there is no element a of {1, 2, 3} such that q(a).
Abstraction
When trying to write sets as rosters, we quickly discover issues with the technique. Since the rational numbers are defined using integers, we suspect that Q can be written as a roster, but when we try to begin a list, such as
![]()
we realize that there are complications with the pattern and are not quite sure that the we will exhaust them all. When considering R, we know immediately that a roster is out of the question. We conclude that we need another method.
Fix a first-order alphabet with theory symbols S. Let A be a set and S-formula p(x) have the property that for every a,
![]()
Notice that p(x) completely describes the members of A. Namely, whenever we write a ∈ A, we can also write p(a), and, conversely, whenever we write p(a), we can also write a ∈ A. For example, let E be the set of even integers. As a roster,
![]()
![]()
The even integers are exactly those numbers x such that p(x). In particular, we have p(2) and p(−4) but not p(5). Therefore, 2 and −4 are elements of E, but 5 is not.
![]() DEFINITION 3.1.8
DEFINITION 3.1.8
Let A be a first-order alphabet with theory symbols S. Let p(x) be an S-formula and A be a set. Write A = {x : p(x)} to mean
![]()
Using {x : p(x)} to identify A is called the method of abstraction.
Using Definition 3.1.8 and (3.1), write E using abstraction as
![]()
or
![]()
Read this as “the set of x such that p(x).” Because x = 2n, it is customary to remove x from the definition of sets like E and write
![]()
or
![]()
Read this as “the set of all 2n such that n is an integer.” This simplified notation is still considered abstraction. Its form can be summarized as
![]()
That is, what the elements look like come before the colon, and the condition that must be satisfied to be an element of the set comes after the colon.
![]() EXAMPLE 3.1.9
EXAMPLE 3.1.9
Given the quadratic equation x2 − x − 2 = 0, we know that its solutions are −1 and 2. Thus, its solution set is A = {−1, 2}. Using the method of abstraction, this can be written as
![]()
However, as we have seen, it is customary to write the formula so that it is easier to read, so
![]()
![]()
Therefore, given an arbitrary polynomial f(x), its solution set over the real numbers is
![]()
![]() EXAMPLE 3.1.10
EXAMPLE 3.1.10
Since x ∉ ∅ is always true, to write the empty set using abstraction, we use a formula like x ≠ x or a contradiction like P ∧ ¬P, where P is a propositional form. Then,
![]()
![]() EXAMPLE 3.1.11
EXAMPLE 3.1.11
Using the natural numbers as the starting point, Z and Q can be defined using the abstraction method by writing
![]()
and
![]()
Notice the redundancy in the definition of Q. The fraction 1/2 is named multiple times like 2/4 or 9/18, but remember that this does not mean that the numbers appear infinitely many times in the set. They appear only once.
![]() EXAMPLE 3.1.12
EXAMPLE 3.1.12
The open intervals can be defined using abstraction.

See Exercise 9 for the closed and half-open intervals. Also, as with Z+ and Z−, the superscript + or − is always used to denote the positive or negative numbers, respectively, of a set. For example,
![]()
and
![]()
Each of the following are written using the abstraction method and, where appropriate, as a roster.
- The set of all rational numbers with denominator equal to 3 in roster form is

Using abstraction, it is

- The set of all linear polynomials with integer coefficients and leading coefficient equal to 1 is

Using abstraction it is

- The set of all polynomials of degree at most 5 can be written as

Exercises
1. Determine whether the given propositions are true or false.
(a) 0 ∈ N
(b) 1/2 ∈ Z
(c) −4 ∈ Q
(d) 4 + π ∈ R
(e) 4.34534 ∈ C
(f) {1, 2} = {2, 1}
(g) {1, 2} = {1, 2, 1}
(h) [1, 2] = {1, 2}
(i) (1, 3) = {2}
(j) −1 ∈ (−∞, −1)
(k) −1 ∈ [−1, ∞)
(l) ∅ ∈ (−2, 2)
(m) ∅ ∈ ∅
(n) 0 ∈ ∅
2. Write the given sets as rosters.
(a) The set of all integers between 1 and 5 inclusive
(b) The set of all odd integers
(c) The set of all nonnegative integers
(d) The set of integers in the interval (−3, 7]
(e) The set of rational numbers in the interval (0, 1) that can be represented with exactly two decimal places
3. If possible, find an element a in the given set such that a + 3.14 = 0.
(a) Z
(b) R
(c) R+
(d) R−
(e) Q
(f) C
(g) (0, 6)
(h) (−∞, −1)
4. Determine whether the following are true or false.
(a) 1 ∈ {x : p(x)} when ¬p(1)
(b) 7 ∈ {x ∈ R : x2 − 5x − 14 = 0}
(c) 7x2 − 0.5x ∈ {a2x2 + a1x + a0 : ai ∈ Q}
(d) xy ∈ {2k : k ∈ Z} if x is even and y is odd.
(e) cos θ ∈ {a cos θ + b sin θ : a, b ∈ R}
(f) {1, 3} = {x : (x − 1)(x − 3) = 0}
(g) {1, 3} = {x : (x − 1)(x − 3)2 = 0}
![]()
5. Write the following given sets in roster form.
(a) {−3n : n ∈ Z}
(b) {0 · n : n ∈ R}
(c) {n cos x : n ∈ Z}
(d) {ax2 + ax + a : a ∈ N}
![]()
6. Use a formula to uniquely describe the elements in the following sets. For example, x ∈ N if and only if x ∈ Z ∧ x ≥ 0.
(a) (0, 1)
(b) (−3, 3]
(c) [0, ∞)
(d) Z+
(e) {..., −2, −1, 0, 1, 2,...}
(f) {2a, 4a, 6a, ...}
7. Write each set using the method of abstraction.
(a) All odd integers
(b) All positive rational numbers
(c) All integer multiples of 7
(d) All integers that have a remainder of 1 when divided by 3
(e) All ordered pairs of real numbers in which the x-coordinate is positive and the y-coordinate is negative
(f) All complex numbers whose real part is 0
(g) All closed intervals that contain π
(h) All open intervals that do not contain a rational number
(i) All closed rays that contain no numbers in (−∞, 3]
(j) All 2 × 2 matrices with real entries that have a diagonal sum of 0
(k) All polynomials of degree at most 3 with real coefficients
8. Write the given sets of real numbers using interval notation.
(a) The set of real numbers greater than 4
(b) The set of real numbers between −6 and −5 inclusive
(c) The set of real numbers x so that x < 5
(d) The set of real numbers x such that 10 < x ≤ 14
9. Let a, b ∈ R with a < b. Write the given intervals using the abstraction method.
(a) [a, b]
(b) [a, ∞)
(c) (−∞, b]
(d) (a, b]
3.2 SET OPERATIONS
We now use connectives to define the set operations. These allow us to build new sets from given ones.
Union and Intersection
The first set operation is defined using the ∨ connective.
![]() DEFINITION 3.2.1
DEFINITION 3.2.1
The union of A and B is
![]()
The union of sets can be viewed as the combination of all elements from the sets. On the other hand, the next set operation is defined with ∧ and can be considered as the overlap between the given sets.
![]() DEFINITION 3.2.2
DEFINITION 3.2.2
The intersection of A and B is
![]()
Figure 3.2 Venn diagrams for union and intersection.
For example, if A = {1, 2, 3, 4} and B = {3, 4, 5, 6}, then
![]()
and
![]()
The operations of union and intersection can be illustrated with pictures called Venn diagrams, named after the logician John Venn who used a variation of these drawings in his text on symbolic logic (Venn 1894). First, assume that all elements are members of a fixed universe U (page 97). In set theory, the universe is considered to be the set of all possible elements in a given situation. Use circles to represent sets and a rectangle to represent U. The space inside these shapes represent where elements might exist. Shading is used to represent where elements might exist after applying some set operations. The Venn diagram for union is in Figure 3.2(a) and the one for intersection is in Figure 3.2(b). If sets have no elements in their intersection, we can use the next definition to name them.
![]() DEFINITION 3.2.3
DEFINITION 3.2.3
The sets A and B are disjoint or mutually exclusive when A ∩ B = ∅.
The sets {1, 2, 3} and {6, 7} are disjoint. A Venn diagram for two disjoint sets is given in Figure 3.3.
Set Difference
The next two set operations take all of the elements of one set that are not in another. They are defined using the not connective.
![]() DEFINITION 3.2.4
DEFINITION 3.2.4
The set difference of B from A is
![]()
Figure 3.3 A Venn diagram for disjoint sets.
The complement of A is defined as
![]()
Read A B as “A minus B” or “A without B.” See Figure 3.4(a) for the Venn diagram of the set difference of sets and Figure 3.4(b) for the complement of a set.
![]() EXAMPLE 3.2.5
EXAMPLE 3.2.5
The following equalities use set difference.
- N = Z Z−
- The set of irrational numbers is R Q.
- R = C {a + bi : a, b ∈ R ∧ b ≠ 0}

Figure 3.4 Venn diagrams for set difference and complement.
Let U = {1, 2, ... , 10}. Use a Venn diagram to find the results of the set operations on A = {1, 2, 3, 4, 5} and B = {3, 4, 5, 6, 7, 8}. Each element will be represented as a point and labeled with a number.

- A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}
- A ∩ B = {3, 4, 5}
- A B = {1, 2}
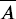 = {6, 7, 8, 9, 10}
= {6, 7, 8, 9, 10}
![]() EXAMPLE 3.2.7
EXAMPLE 3.2.7
Let C = (−4, 2), D = [−1, 3], and U = R. Use the diagram to perform the set operations.

- C ∪ D = (−4, 3]
- C ∩ D = [−1, 2)
- C D = (−4, −1)
 = (−∞, −4] ∪ [2, ∞)
= (−∞, −4] ∪ [2, ∞)
Cartesian Products
The last set operation is not related to the logic connectives as the others, but it is nonetheless very important to mathematics. Let A and B be sets. Given elements a ∈ A and b ∈ B, we call (a, b) an ordered pair. In this context, a and b are called coordinates. It is similar to the set {a, b} except that the order matters. The definition is due to Kazimierz Kuratowski (1921).
![]() DEFINITION 3.2.8
DEFINITION 3.2.8
If a ∈ A and b ∈ B,
![]()
Notice that (a, b) = (a′, b′) means that
![]()
which implies that a = a′ and b = b′. Therefore,
![]()
The set of all ordered pairs with the first coordinate from A and the second from B is named after René Descartes.
![]() DEFINITION 3.2.9
DEFINITION 3.2.9
The Cartesian product of A and B is
![]()
The product R2 = R × R is the set of ordered pairs of the Cartesian plane.
![]() EXAMPLE 3.2.10
EXAMPLE 3.2.10
- Since (1, 2) ≠ (2, 1),

Even though we have a set definition for an ordered pair, we can still visually represent this set on a grid as in Figure 3.5(a).
- If A = {1, 2, 7} and B = {∅, {1, 5}},

See Figure 3.5(b).
- For any set A, ∅ × A = A × ∅ = ∅ because ¬∃x(x ∈ ∅ ∧ y ∈ A).
Figure 3.5 Two Cartesian products.
We generalize Definition 3.2.8 by defining

and for n ∈ N,
![]()
which is called an ordered n-tuple. Then,

and
![]()
Specifically, R3 = R × R × R, and

which is known as Cartesian n-space.
![]() EXAMPLE 3.2.11
EXAMPLE 3.2.11
Let A = {1}, B = {2}, C = {3}, and D = {4}. Then,
![]()
is a singleton containing an ordered 4-tuple. Also,
![]()
but
![]()
Order of Operations
As with the logical connectives, we need an order to make sense of expressions that involve many operations. To do this, we note the association between the set operations and certain logical connectives.

From this we derive the order for the set operations.
![]() DEFINITION 3.2.12 [Order of Operations]
DEFINITION 3.2.12 [Order of Operations]
To find a set determined by set operations, read from left to right and use the following precedence.
- sets within parentheses (innermost first),
- complements,
- set differences,
- intersections,
- unions.
![]() EXAMPLE 3.2.13
EXAMPLE 3.2.13
If the universe is taken to be {1, 2, 3, 4, 5}, then
![]()
This set can be written using parentheses as
![]()
However,
![]()
showing that
![]()
Define A = {1}, B = {2}, C = {3}, and D = {4}. Then, we have
![]()
Written with parentheses and brackets,
![]()
With the given assignments, A ∩ B ∩ C ∩ D is empty.
Exercises
1. Each of the given propositions are false. Replace the underlined word with another word to make the proposition true.
(a) Intersection is defined using a disjunction.
(b) Set diagrams are used to illustrate set operations.
(c) R (R Q) is the set of irrational numbers.
(d) Set difference has a higher order of precedence than complements.
(e) The complement of A is equal to R set minus A.
(f) The intersection of two intervals is always an interval.
(g) The union of two intervals is never an interval.
(h) A × B is equal to ∅ if B does not contain ordered pairs.
2. Let A = {0, 2, 4, 6}, B = {3, 4, 5, 6}, C = {0, 1, 2}, and U = {0, 1, ... , 9, 10}. Write the given sets in roster notation.
(a) A ∪ B
(b) A ∩ B
(c) A B
(d) B A
(e) ![]()
(f) A × B
(g) A ∪ B ∩ C
(h) A ∩ B ∪ C
(i) ![]() ∩ B
∩ B
(j) A ∪ ![]()
(k) A B C
(l) A ∪ B A ∩ C
3. Write each of the given sets using interval notation.
(a) [2, 3] ∩ (5/2, 7]
(b) (−∞, 4) ∪ (−6, ∞)
(c) (−2, 4) ∩ [−6, ∞)
(d) ∅ ∪ (4, 12]
4. Identify each of the the given sets.
(a) [6, 17] ∩ [17, 32)
(b) [6, 17) ∩ [17, 32)
(c) [6, 17] ∪ (17, 32)
(d) [6, 17) ∪ (17, 32)
5. Draw Venn diagrams.
(a) A ∩ ![]()
(b) ![]()
(c) A ∩ ![]() ∪
∪ ![]()
(d) (A ∪ B) ![]()
(e) A ∩ C ∩ ![]()
(f) ![]()
6. Match each Venn diagram to as many sets as possible.

(a) A ∪ B
(b) A B
(c) A ∩ ![]()
(d) (A ∪ B) (A ∩ B)
(e) A ∩ B ∪ A ∩ C ∪ B ∩ C
(f) ![]()
(g) (A ∪ B) ∩ (![]() ∪
∪ ![]() )
)
(h) [(A ∪ B) ∩ ![]() ] ∪ [(A ∪ B) ∩ C]
] ∪ [(A ∪ B) ∩ C]
(i) [![]() ∩
∩ ![]() ) ∩ C] ∪ [
) ∩ C] ∪ [![]() ∩
∩ ![]() ∩
∩ ![]() ]
]
![]()
7. The ordered pair (1, 2) is paired with the ordered pair (2, 1) using a set operation. Write each resulting set as a roster.
(a) (1, 2) ∪ (2, 1)
(b) (1, 2) ∩ (2, 1)
(c) (1, 2) (2, 1)
8. Let p(x) be a formula. Prove the following.
(a) ∀x[x ∈ A ∪ B → p(x)] ⇒ ∀x[x ∈ A ∩ B → p(x)]
(b) ∀x[x ∈ A ∪ B → p(x)] ⇔ ∀x[x ∈ A → p(x)] ∧ ∀x[x ∈ B → p(x)]
(c) ∃x[x ∈ A ∩ B ∧ p(x)] ⇒ ∃x[x ∈ A ∧ p(x)] ∧ ∃x[x ∈ B ∧ p(x)]
(d) ∃x[x ∈ A ∪ B ∧ p(x)] ⇔ ∃x[x ∈ A ∧ p(x)] ∨ ∃x[x ∈ B ∧ p(x)]
9. Find a formula p(x) and sets A and B to show that the following are false.
(a) ∀x[x ∈ A → p(x)] ∨ ∀x[x ∈ B → p(x)] ⇒ ∀x[x ∈ A ∪ B → p(x)]
(b) ∃x[x ∈ A ∧ p(x)] ∧ ∃x[x ∈ B ∧ p(x)] ⇒ ∃x[x ∈ A ∩ B ∧ p(x)]
3.3 SETS WITHIN SETS
An important relation between any two sets is when one is contained within another.
Subsets
Let A and B be sets. A is a subset of B exactly when every element of A is also an element of B, in symbols A ⊆ B. This is represented in a Venn diagram by the circle for A being within the circle for B [Figure 3.6(a)].
![]() DEFINITION 3.3.1
DEFINITION 3.3.1
For all sets A and B,
![]()
If A is not a subset of B, write A ![]() B. This is represented in a Venn diagram by A overlapping B with a point in A but not within B [Figure 3.6(b)]. Logically, this means
B. This is represented in a Venn diagram by A overlapping B with a point in A but not within B [Figure 3.6(b)]. Logically, this means
![]()
Thus, to show A ![]() B find an element in A that is not in B. For example, if we let A = {1, 2, 3} and B = {1, 2, 5}, then A
B find an element in A that is not in B. For example, if we let A = {1, 2, 3} and B = {1, 2, 5}, then A ![]() B because 3 ∈ A but 3 ∉ B.
B because 3 ∈ A but 3 ∉ B.

Figure 3.6 Venn diagrams for a subset and a nonsubset.
The proposition for all sets A and B, A ∪ B ⊆ A is false. To see this, we must prove that there exists A and B such that A ∪ B ![]() A. We take A = {1} and B = {2} as our candidates. Since A ∪ B = {1, 2} and 2 ∉ A, we have A ∪ B
A. We take A = {1} and B = {2} as our candidates. Since A ∪ B = {1, 2} and 2 ∉ A, we have A ∪ B ![]() A.
A.
Every set is the improper subset of itself. The notation A ⊂ B means A ⊆ B but A ≠ B. In this case, A is a proper subset of B.
![]() EXAMPLE 3.3.3
EXAMPLE 3.3.3
- {1, 2, 3} ⊂ {1, 2, 3, 4, 5} and {1, 2, 3} ⊆ {1, 2, 3}
- N ⊂ Z ⊂ Q ⊂ R ⊂ C
- (4, 5) ⊂ (4, 5] ⊂ [4, 5]
- {1, 2, 3} is not a subset of {1, 2, 4}.
Our study of subsets begins with a fundamental theorem. It states that the empty set is a subset of every set.
![]() THEOREM 3.3.4
THEOREM 3.3.4
∅ ⊆ A.
PROOF
Let A be a set. Since x ∉ ∅, we have
![]()
Proving that one set is a subset of another always means proving an implication, so Direct Proof is the primary tool in these proofs. That is, usually to prove that a set A is a subset of a set B, take an element x ∈ A and show x ∈ B.
![]() EXAMPLE 3.3.5
EXAMPLE 3.3.5
- Let x ∈ Z N. Then, x ∈ Z but x ∉ N, so x ∈ Z by Simp. Thus, Z N ⊆ Z.
- Let

and
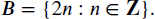
Take x ∈ A. This means that

In other words,


We have two cases to check. If x − 2n = 0, then x = 2n. This means x ∈ B. If x − 2n − 2 = 0, then x = 2n + 2 = 2(n + 1), which also means x ∈ B since n + 1 is an integer. Hence, A ⊆ B.
- Fix a, b ∈ Z. Let x = na, some n ∈ Z. This means x = na + 0b, which implies that {na : n ∈ Z} ⊆ {na + mb : n, m ∈ Z}.
This next result is based only on the definitions and Inference Rules 1.2.10. As with Section 3.2, we see the close ties between set theory and logic.
![]() THEOREM 3.3.6
THEOREM 3.3.6
- A ⊆ A.
- If A ⊆ B and B ⊆ C, then A ⊆ C.
- If A ⊆ B and x ∈ A, then x ∈ B.
- If A ⊆ B and x ∉ B, then x ∉ A.
- Let A ⊆ B and C ⊆ D. If x ∈ A or x ∈ C, then x ∈ B or x ∈ D.
- Let A ⊆ B and C ⊆ D. If x ∉ B or x ∉ D, then x ∉ A or x ∉ C.
PROOF
Assume A ⊆ B and B ⊆ C. By definition, x ∈ A implies x ∈ B and x ∈ B implies x ∈ C. Therefore, by HS, if x ∈ A, then x ∈ C. In other words, A ⊆ C. The remaining parts are left to Exercise 4. ![]()
Note that it is not the case that for all sets A and B, A ⊆ B implies that B ⊆ A. To prove this, choose A = ∅ and B = {0}. Then, A ⊆ B yet B ![]() A because 0 ∈ B and 0 ∉ ∅.
A because 0 ∈ B and 0 ∉ ∅.
Equality
For two sets to be equal, they must contain exactly the same elements (page 118 of Section 3.1). This can be stated more precisely using the idea of a subset.
![]() DEFINITION 3.3.7
DEFINITION 3.3.7
A = B means A ⊆ B and B ⊆ A.
To prove that two sets are equal, we show both inclusions. Let us do this to prove ![]() . This is one of De Morgan's laws. To prove it, we demonstrate both
. This is one of De Morgan's laws. To prove it, we demonstrate both
![]()
![]()
This amounts to proving a biconditional, which means we will use the rule of biconditional proof. Look at the first direction:

Now read backward through those steps. Each follows logically when read in this order because only definitions and replacement rules were used. This means that the steps are reversible. Hence, we have a series of biconditionals, and we can use the short rule of biconditional proof (page 108):

Hence, ![]()
We must be careful when writing these types of proofs since it is easy to confuse the notation.
- The correct translation for x ∈ A ∩ B is x ∈ A ∧ x ∈ B. Common mistakes for this translation include using formulas with set operations:

... and sets with connectives:

Remember that connectives connect formulas and set operations connect sets.
- Negations also pose problems. If a complement is used, first translate using

and then proceed with the proof. Similarly, the formula x ∉ A ∪ B can be written as neither x ∉ A ∪ x ∉ B nor x ∉ A ∨ x ∉ B. Instead, use DeM:

We can now prove many basic properties about set operations. Notice how the following are closely related to their corresponding replacement rules (1.3.9).
![]() THEOREM 3.3.8
THEOREM 3.3.8
- Associative Laws
A ∩ B ∩ C = A ∩ (B ∩ C)
A ∪ B ∪ C = A ∪ (B ∪ C)
- Commutative Laws
A ∩ B = B ∩ A
A ∪ B = B ∪ A
- De Morgan's Laws

- Distributive Laws
A ∩ (B ∪ C) = A ∩ B ∪ A ∩ C
A ∪ B ∩ C = (A ∪ B) ∩ (A ∪ C)
- Idempotent Laws
A ∩ A = A
A ∪ A = A.
![]() EXAMPLE 3.3.9
EXAMPLE 3.3.9
We use the short rule of biconditional proof (page 108) to prove the equality A ∩ B ∩ C = A ∩ (B ∩ C).

Another way to prove it is to use a chain of equal signs.

We have to be careful when proving equality. If two sets are equal, there are always proofs for both inclusions. However, the steps needed for the one implication might not simply be the steps for the converse in reverse. The next example illustrates this. It is always true that A ∩ B ⊆ A. However, the premise is needed to show the other inclusion.
![]() EXAMPLE 3.3.10
EXAMPLE 3.3.10
Let A ⊆ B. Prove A ∩ B = A.
- Let x ∈ A ∩ B. This means that x ∈ A and x ∈ B. Then, x ∈ A (Simp).
- Assume that x is an element of A. Since A ⊆ B, x is also an element of B. Hence, x ∈ A ∩ B.
A more involved example of this uses the concept of divisibility. Let a, b ∈ Z, not both equal to zero. A common divisor of a and b is c when c | a and c | b. For example, 4 is a common divisor of 48 and 36, but it is not the largest.
![]() DEFINITION 3.3.11
DEFINITION 3.3.11
Let a, b ∈ Z with a and b not both zero. The integer g is the greatest common divisor of a and b if g is a common divisor of a and b and e ≤ g for every common divisor e ∈ Z. In this case, write g = gcd(a, b).
For example,
![]()
and
![]()
Notice that it is important that at least one of the integers is not zero. The gcd(0, 0) is undefined since all a such that a ≠ 0 divide 0. Further notice that the greatest common divisor is positive.
![]() EXAMPLE 3.3.12
EXAMPLE 3.3.12
Let a, b ∈ Z. Prove for all n ∈ Z,
![]()
If both pairs of numbers have the same common divisors, their greatest common divisors must be equal. So, define
![]()
and
![]()
To show that the greatest common divisors are equal, prove S = T.
- Let d ∈ S. Then d | a + nb and d | b. This means a + nb = dl and b = dk for some l, k ∈ Z. We are left to show d | a. By substitution, a + ndk = dl. Hence, d ∈ T because

- Now take d ∈ T. This means d | a and d | b. Thus, there exists l, k ∈ Z such that a = dl and b = dk. Then,

Therefore, d | a + nb and d ∈ S.
As with subsets, let us now prove some results concerning the empty set and the universe. We use two strategies.
- Let A be a set. We know that

Therefore, to prove that A is empty, take an arbitrary a and show a ∉ A. This can sometimes be done directly, but more often an indirect proof is better. That is, assume a ∈ A and derive a contradiction. Since the contradiction arose simply by assuming a ∈ A, this formula must be the problem. Hence, A can have no elements.
- Let U be a universe. To prove A = U, we must show that A ⊆ U and U ⊆ A. The first subset relation is always true. To prove the second, take an arbitrary element and show that it belongs to A. This works because U contains all possible elements.
![]() EXAMPLE 3.3.13
EXAMPLE 3.3.13
- Suppose x ∈ A ∩ ∅. Then x ∈ ∅, which is impossible. Therefore, A ∩ ∅ = ∅.
- Certainly, A ⊆ A ∪ ∅, so to show the opposite inclusion take x ∈ A ∪ ∅. Since x ∉ ∅, it must be the case that x ∈ A. Thus, A ∪ ∅ ⊆ A, and we have that A ∪ ∅ = A.
- From Exercise 5(b), we know A ∩ U ⊆ A, so let x ∈ A. This means that x must also belong to the universe. Hence, x ∈ A ∩ U, so A ∩ U = A.
- Certainly, A ∪ U ⊆ U. Moreover, by Exercise 5(c), we have the other inclusion. Thus, A ∪ U = U.
To prove that a set A is not equal to the empty set, show ¬∀x(x ∉ A), but this is equivalent to ∃x(x ∈ A). For instance, let
![]()
We know that A is nonempty since −1 ∈ A.
![]() EXAMPLE 3.3.15
EXAMPLE 3.3.15
Let
![]()
and
![]()
These sets are not disjoint since (0, 0) is an element of both A and B. However, A ≠ B because (1, −1) ∈ A but (1, −1) ∉ B.
Let us combine the two strategies to show a relationship between ∅ and U.
![]() THEOREM 3.3.16
THEOREM 3.3.16
For all sets A and B and universe U, the following are equivalent.
- A ⊆ B
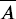 ∪ B = U
∪ B = U- A ∩
 = ∅.
= ∅.
PROOF
- Assume A ⊆ B. Suppose x ∉
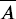 . Then, x ∈ A, which implies that x ∈ B. Hence, for every element x, we have that x ∈
. Then, x ∈ A, which implies that x ∈ B. Hence, for every element x, we have that x ∈ 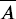 or x ∈ B, and we conclude that
or x ∈ B, and we conclude that 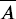 ∪ B = U.
∪ B = U. - Suppose
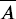 ∪ B = U. In order to obtain a contradiction, take x ∈ A ∩
∪ B = U. In order to obtain a contradiction, take x ∈ A ∩  . Then, x ∈
. Then, x ∈  . Since x ∈ A, the supposition also gives x ∈ B, a contradiction. Therefore, A ∩
. Since x ∈ A, the supposition also gives x ∈ B, a contradiction. Therefore, A ∩  = ∅.
= ∅. - Let A ∩
 = ∅. Assume x ∈ A. By hypothesis, x cannot be a member of
= ∅. Assume x ∈ A. By hypothesis, x cannot be a member of  , otherwise the intersection would be nonempty. Hence, x ∈ B.
, otherwise the intersection would be nonempty. Hence, x ∈ B. 
The following theorem is a generalization of the corresponding result concerning subsets. The proof could have been written using the short rule of biconditional proof or by appealing to Lemma 3.3.6 (Exercise 21).
![]() THEOREM 3.3.17
THEOREM 3.3.17
If A = B and B = C, then A = C.
Assume A = B and B = C. This means A ⊆ B, B ⊆ A, B ⊆ C, and C ⊆ B. We must show that A = C.
- Let x ∈ A. By hypothesis, x is then an element of B, which implies that x ∈ C.
- Let x ∈ C. Then, x ∈ B, from which x ∈ A follows.

The last result of the section involves the Cartesian product. The first part is illustrated in Figure 3.7. The sets B and C are illustrated along the vertical axis and A is illustrated along the horizontal axis. The Cartesian products are represented as boxes. The other parts of the theorem can be similarly visualized.
![]() THEOREM 3.3.18
THEOREM 3.3.18
- A × (B ∩ C) = (A × B) ∩ (A × C).
- A × (B ∪ C) = (A × B) ∪ (A × C).
- A × (B C) = (A × B) (A × C).
- (A × B) ∩ (C × D) = (A ∩ C) × (B ∩ D).
PROOF
We prove the first equation. The last three are left to Exercise 19. Take three sets A, B, and C. Then,


Figure 3.7 A × (B ∩ C) = (A × B) ∩ (A × C).
Inspired by the last result, we might try proving that (A × B) ∪ (C × D) is always equal to (A ∪ C) × (B ∪ D), but no such proof exists. To show this, take A = B = {1} and C = D = {2}. Then
![]()
but
![]()
Hence, (A ∪ C) × (B ∪ D) ![]() (A × B) ∪ (C × D). Notice, however, that the opposite inclusion is always true (Exercise 3.3.8).
(A × B) ∪ (C × D). Notice, however, that the opposite inclusion is always true (Exercise 3.3.8).
Exercises
1. Answer true or false.
(a) ∅ ∈ ∅
(b) ∅ ⊆ {1}
(c) 1 ∈ Z
(d) 1 ⊆ Z
(e) 1 ∈ ∅
(f) {1} ⊆ ∅
(g) 0 ∈ ∅
(h) {1} ∈ Z
(i) ∅ ⊆ ∅
2. Answer true or false. For each false proposition, find one element that is in the first set but is not in the second.
(a) Z+ ⊆ C
(b) Q+ ⊆ Z+
(c) Q R ⊆ Z
(d) R Q ⊆ Z
(e) Z ∩ (−1, 1) ⊆ Q
(f) (0, 1) ⊆ Q+
(g) (0, 1) ⊆ {0, 1, 2}
(h) (0, 1) ⊆ (0, 1]
3. Prove.
(a) {x ∈ R : x2 − 3x + 2 = 0} ⊆ N
(b) (0, 1) ⊆ [0, 1]
(c) [0, 1] ![]() (0, 1)
(0, 1)
(d) Z × Z ![]() Z × N
Z × N
(e) (0, 1) ∩ Q ![]() [0, 1] ∩ Z
[0, 1] ∩ Z
(f) R ⊆ C
(g) {bi : b ∈ R} ⊆ C
(h) C ![]() R
R
4. Prove the remaining parts of Theorem 3.3.6.
5. Prove.
(a) A ⊆ U
(b) A ∩ B ⊆ A
(c) A ⊆ A ∪ B
(d) A B ⊆ A
(e) If A ⊆ B, then A ∪ C ⊆ B ∪ C.
(f) If A ⊆ B, then A ∩ C ⊆ B ∩ C.
(g) If A ⊆ B, then C B ⊆ C A.
(h) If A ≠ ∅, then A ![]()
![]() .
.
(i) If A ⊆ ![]() , then B ⊆
, then B ⊆ ![]() .
.
(j) If A ⊆ B, then {1} × A ⊆ {1} × B.
(k) If A ⊆ C and B ⊆ D, then A × B ⊆ C × D.
(l) If A ⊆ C and B ⊆ D, then ![]()
6. Prove that A ⊆ B if and only if ![]() ⊆
⊆ ![]() .
.
7. Show that the given proposition is false:
![]()
8. Prove: (A × B) ∪ (C × D) ⊆ (A ∪ C) × (B ∪ D).
9. Take a, b, c ∈ N. Let A = {n ∈ N : n | a} and C = {n ∈ N : n | c}. Suppose a | b and b | c. Prove A ⊆ C.
10. Prove.
(a) B ⊆ A and C ⊆ A if and only if B ∪ C ⊆ A.
(b) A ⊆ B and A ⊆ C if and only if A ⊆ B ∩ C.
11. Prove the unproven parts of Theorem 3.3.8.
12. Prove each equality.
(a) ![]() = U
= U
(b) ![]() = ∅
= ∅
(c) A ∩ ![]() = ∅
= ∅
(d) A ∪ ![]() = U
= U
(e) ![]() = A
= A
(f) A A = ∅
(g) A ∅ = A
(h) ![]() ∩ B = B A
∩ B = B A
(i) A B = A ∩ ![]()
(j) ![]() ∩ B = ∅
∩ B = ∅
(k) A ∩ B A = ∅
13. Sketch a Venn diagram for each problem and then write a proof.
(a) A = A ∩ B ∪ A ∩ ![]()
(b) A ∪ B = A ∪ ![]() ∩ B
∩ B
(c) A (B C) = A ∩(![]() ∪ C)
∪ C)
(d) A (A ∩ B) = A B
(e) A ∩ B ∪ A ∩ ![]() ∪
∪ ![]() ∩ B = A ∪ B
∩ B = A ∪ B
(f) (A ∪ B) C = A C ∪ B C
(g) A (B C) = A B ∪ A ∩ C
(h) A B C = A (B ∪ C)
14. Prove.
(a) If A ⊆ B, then A B = ∅.
(b) If A ⊆ ∅, then A = ∅.
(c) Let U be a universe. If U ⊆ A, then A = U.
(d) If A ⊆ B, then B (B A) = A.
(e) A × B = ∅ if and only if A = ∅ or
15. Let a, c, m ∈ Z and define A = {a + mk : k ∈ Z} and B = {a + m(c + k) : k ∈ Z}. Show A = B.
16. Prove A = B, where
![]()
and
![]()
17. Prove.
(a) Q ≠ Z
(b) C ≠ R
(c) {0} × Z ≠ Z
(d) R × Z ≠ Z × R
(e) If A = {ax3 + b : a, b ∈ R} and B = {x3 + b : b ∈ R}, then A ≠ B.
(f) If A = {ax3 + b : a, b ∈ Z} and B = {ax3 + b : a, b ∈ C}, then A ≠ B.
(g) A ≠ B, where
![]()
and
![]()
18. Find A and B to illustrate the given inequalities.
(a) A B ≠ B A
(b) (A × B) × C ≠ A × (B × C)
(c) A × B ≠ B × A
19. For the remaining parts of Theorem 3.3.18, draw diagrams as in Figure 3.7 and prove the results.
20. Is it possible for A = ![]() ? Explain.
? Explain.
21. Prove Theorem 3.3.17 by first using the short rule of biconditional proof and then by directly appealing to Theorem 3.3.6.
22. Prove that the following are equivalent.
- A ⊆ B
- A ∪ B = B
- A B = ∅
- A ∩ B = A
23. Prove that the following are equivalent.
- A ∩ B = ∅
- A
 = ∅
= ∅ - A ⊆

24. Find an example of sets A, B, and C such that A ∩ B = A ∩ C but B ≠ C.
25. Does A ∪ B = A ∪ C imply B = C for all sets A and B? Explain.
26. Prove.
(a) If A ∪ B ⊆ A ∩ B, then A = B.
(b) If A ∩ B = A ∩ C and A ∪ B = A ∪ C, then B = C.
27. Prove that there is a cancellation law with the Cartesian product. Namely, if A ≠ ∅ and A × B = A × C, then B = C.
28. When does A × B = C × D imply that A = C and B = D?
29. Prove.
(a) If A ∪ B ≠ ∅, then A ≠ ∅ or B ≠ ∅.
(b) If A ∩ B ≠ ∅, then A ≠ ∅ and B ≠ ∅.
30. Find the greatest common divisors of each pair.
(a) 12 and 18
(b) 3 and 9
(c) 14 and 0
(d) 7 and 15
31. Let a be a positive integer. Find the following and prove the result.
(a) gcd(a, a + 1)
(b) gcd(a, 2a)
(c) gcd(a, a2)
(d) gcd(a, 0)
3.4 FAMILIES OF SETS
The elements of a set can be sets themselves. We call such a collection a family of sets and often use capital script letters to name them. For example, let
![]()
The set ![]() has three elements: {1, 2, 3}, {2, 3, 4}, and {3, 4, 5}.
has three elements: {1, 2, 3}, {2, 3, 4}, and {3, 4, 5}.
![]() EXAMPLE 3.4.1
EXAMPLE 3.4.1
- {1, 2, 3} ∈ {{1, 2, 3}, {1, 4, 9}}
- 1 ∉ {{1, 2, 3}, {1, 4, 9}}
- {1, 2, 3}
 {{1, 2, 3}, {1, 4, 9}}
{{1, 2, 3}, {1, 4, 9}} - {{1, 2, 3}} ⊆ {{1, 2, 3}, {1, 4, 9}}.
![]() EXAMPLE 3.4.2
EXAMPLE 3.4.2
- ∅ ⊆ {∅, {∅}} by Theorem 3.3.4.
- {∅} ⊆ {∅, {∅}} because ∅ ∈ {∅, {∅}}.
- {{∅}} ⊆ {∅, {∅}} because {∅} ∈ {∅, {∅}}.
Families of sets can have infinitely many elements. For example, let
![]()
In roster notation,
![]()
Notice that in this case, abstraction is more convenient. For each integer n, the closed interval [n, n + 1] is in ![]() . The set Z plays the role of an index set, a set whose only purpose is to enumerate the elements of the family. Each element of an index set is called an index. If we let I = Z and Ai = [i, i + 1], the family can be written as
. The set Z plays the role of an index set, a set whose only purpose is to enumerate the elements of the family. Each element of an index set is called an index. If we let I = Z and Ai = [i, i + 1], the family can be written as
![]()
To write the family ![]() (3.2) using an index set, let I = {0, 1, 2} and define
(3.2) using an index set, let I = {0, 1, 2} and define

Then, the family illustrated in Figure 3.8 is
![]()
Figure 3.8 The family of sets ![]() = {Ai : i ∈ I} with I = {1, 2, 3}.
= {Ai : i ∈ I} with I = {1, 2, 3}.
There is no reason why I must be {0, 1, 2}. Any three-element set will do. The order in which the sets are defined is also irrelevant. For instance, we could have defined I = {w, π, 99} and

The goal is to have each set in the family referenced or indexed by at least one element of the set. We will still have ![]() = {Ai : i ∈ I} with a similar diagram (Figure 3.9).
= {Ai : i ∈ I} with a similar diagram (Figure 3.9).
![]() EXAMPLE 3.4.3
EXAMPLE 3.4.3
Write ![]() (3.3) using N as the index set instead of Z. Use the even natural numbers to index the intervals with a nonnegative integer left-hand endpoint. The odd natural numbers will index the intervals with a negative integer left-hand endpoint. To do this, define the sets Bi as follows:
(3.3) using N as the index set instead of Z. Use the even natural numbers to index the intervals with a nonnegative integer left-hand endpoint. The odd natural numbers will index the intervals with a negative integer left-hand endpoint. To do this, define the sets Bi as follows:

Figure 3.9 The family of sets ![]() = {Ai : i ∈ I} with I = {w, π, 99}.
= {Ai : i ∈ I} with I = {w, π, 99}.
Use 2n + 1 to represent the odd natural numbers and 2n to represent the even natural numbers (n ∈ N). Then,

and

Therefore, define for all natural numbers n,
![]()
and
![]()
We have indexed the elements of ![]() as
as

So under this definition, ![]() = {Bi : i ∈ N}.
= {Bi : i ∈ N}.
Power Set
There is a natural way to form a family of sets. Take a set A. The collection of all subsets of A is called the power set of A. It is represented by P(A).
![]() DEFINITION 3.4.4
DEFINITION 3.4.4
For any set A,
![]()
Notice that ∅ ∈ P(A) by Theorem 3.3.4.
![]() EXAMPLE 3.4.5
EXAMPLE 3.4.5
- P({1, 2, 3}) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
- P({∅, {∅}}) = {∅, {∅}, {{∅}}, {∅, {∅}}}
- P(N) = {∅, {0}, {1}, ... , {0, 1}, {0, 2}, ... }.
Consider A = {2, 6} and B = {2, 6, 10}, so A ⊆ B. Examining the power sets of each, we find that
![]()
and
![]()
Hence, P(A) ⊆ P(B). This result is generalized in the next lemma.
![]() LEMMA 3.4.6
LEMMA 3.4.6
A ⊆ B if and only if P(A) ⊆ P(B).
PROOF
- Let A ⊆ B. Assume X ∈ P(A). Then, X ⊆ A, which gives X ⊆ B by Theorem 3.3.6. Hence, X ∈ P(B).
- Assume P(A) ⊆ P(B). Let x ∈ A. In other words, {x} ⊆ A, but this means that {x} ∈ P(A). Hence, {x} ∈ P(B) by hypothesis, so x ∈ B.

The definition of set equality and Lemma 3.4.6 are used to prove the next theorem. Its proof is left to Exercise 9.
![]() THEOREM 3.4.7
THEOREM 3.4.7
A = B if and only if P(A) = P(B).
Union and Intersection
We now generalize the set operations. Define the union of a family of sets to be the set of all elements that belong to some member of the family. This union is denoted by the same notation as in Definition 3.2.1 and can be defined using the abstraction method.
Let ![]() be a family of sets. Define
be a family of sets. Define
![]()
If the family is indexed so that ![]() = {Ai : i ∈ I}, define
= {Ai : i ∈ I}, define
![]()
Observe that ![]()
![]() =
= ![]() i∈I Ai [Exercise 16(a)].
i∈I Ai [Exercise 16(a)].
We generalize the notion of intersection similarly. The intersection of a family of sets is the set of all elements that belong to each member of the family.
![]() DEFINITION 3.4.9
DEFINITION 3.4.9
Let ![]() be a family of sets.
be a family of sets.
![]()
If the family is indexed so that ![]() = {Ai : i ∈ I}, define
= {Ai : i ∈ I}, define
![]()
Observe that ![]()
![]() =
= ![]() i∈I Ai [Exercise 16(b)].
i∈I Ai [Exercise 16(b)].
Furthermore, notice that both definitions are indeed generalizations of the operations of Section 3.2 because as noted in Exercise 17,
![]()
and
![]()
![]() EXAMPLE 3.4.10
EXAMPLE 3.4.10
Define ![]() = {[n, n + 1] : n ∈ Z}.
= {[n, n + 1] : n ∈ Z}.
- When all of these intervals are combined, the result is the real line. This means that

- There is not one element that is common to all of the intervals. Hence,

The next example illustrates how to write the union or intersection of a family of sets as a roster.
Let ![]() = {{1, 2, 3}, {2, 3, 4}, {3, 4, 5}}.
= {{1, 2, 3}, {2, 3, 4}, {3, 4, 5}}.
- Since 1 is in the first set of
 , 1 ∈
, 1 ∈ 
 . The others can be explained similarly, so
. The others can be explained similarly, so

Notice that mechanically this amounts to removing the braces around the sets of the family and setting the union to the resulting set:

- The generalized intersection is simply the overlap of all of the sets. Hence, 3 is the only element of

 . That is,
. That is,

and this is illustrated by the following diagram:

![]() EXAMPLE 3.4.12
EXAMPLE 3.4.12
Since a family of sets can be empty, we must be able to take the union and intersection of the empty set. To prove that ![]() ∅ = ∅, take x ∈
∅ = ∅, take x ∈ ![]() ∅. This means that there exists A ∈ ∅ such that x ∈ A, but this is impossible. We leave the fact that
∅. This means that there exists A ∈ ∅ such that x ∈ A, but this is impossible. We leave the fact that ![]() ∅ is equal to the universe to Exercise 24.
∅ is equal to the universe to Exercise 24.
The next theorem generalizes the Distributive Laws. Exercise 2.4.10 plays an important role in its proof. It allows us to move the quantifier.
Let Ai (i ∈ I) and B be sets.
PROOF
We leave the second part to Exercise 19. The first part is demonstrated by the following biconditional proof:

To understand the next result, consider the following example. Choose the universe to be {1, 2, 3, 4, 5} and perform some set operations on the family
![]()
First,
![]()
and second,
![]()
This leads us to the next generalization of De Morgan's laws. Its proof is left to Exercise 23.
![]() THEOREM 3.4.14
THEOREM 3.4.14
Let {Ai : i ∈ I} be a family of sets.
Disjoint and Pairwise Disjoint
What it means for two sets to be disjoint was defined in Section 3.2 (Definition 3.2.3). The next definition generalizes that notion to families of sets. Because a family can have more than two elements, it is appropriate to expand the concept of disjointness.
![]() DEFINITION 3.4.15
DEFINITION 3.4.15
Let ![]() be a family of sets.
be a family of sets.
 is disjoint when
is disjoint when 
 = ∅.
= ∅. is pairwise disjoint when for all A, B ∈
is pairwise disjoint when for all A, B ∈  , if A ≠ B, then A ∩ B = ∅.
, if A ≠ B, then A ∩ B = ∅.
Observe that {{1, 2}, {3, 4}, {5, 6}} is both disjoint and pairwise disjoint because its elements have no common members.
![]() EXAMPLE 3.4.16
EXAMPLE 3.4.16
Let A be a set. We see that
![]()
Although P(A) is not a pairwise disjoint family of sets, it is a disjoint because ∅ ∈ P(A).
If the family is indexed, we can use another test to determine if it is pairwise disjoint. Let ![]() = {Ai : i ∈ I} be a family of sets. If for all i, j ∈ I,
= {Ai : i ∈ I} be a family of sets. If for all i, j ∈ I,
![]()
then ![]() is pairwise disjoint. To prove this, let
is pairwise disjoint. To prove this, let ![]() be a family that satisfies (3.4). Take Ai, Aj ∈
be a family that satisfies (3.4). Take Ai, Aj ∈ ![]() for some i, j ∈ I and assume Ai ≠ Aj. Therefore, i ≠ j, for otherwise they would be the equal. Hence, Ai ∩ Aj = ∅ by Condition 3.4.
for some i, j ∈ I and assume Ai ≠ Aj. Therefore, i ≠ j, for otherwise they would be the equal. Hence, Ai ∩ Aj = ∅ by Condition 3.4.
The next result illustrates the relationship between these two terms. One must be careful, though. The converse is false (Exercise 14).
![]() THEOREM 3.4.17
THEOREM 3.4.17
Let ![]() be a family of sets with at least two elements. If
be a family of sets with at least two elements. If ![]() is pairwise disjoint, then
is pairwise disjoint, then ![]() is disjoint.
is disjoint.
PROOF
Assume ![]() is pairwise disjoint. Since
is pairwise disjoint. Since ![]() contains at least two sets, let A, B ∈
contains at least two sets, let A, B ∈ ![]() such that A ≠ B. Then, using Exercise 27,
such that A ≠ B. Then, using Exercise 27, ![]()
![]() ⊆ A ∩ B = ∅.
⊆ A ∩ B = ∅. ![]()
Exercises
1. Let I = {1, 2, 3, 4, 5}, A1 = {1, 2}, A2 = {3, 4}, A3 = {1, 4}, A4 = {3, 4}, and A5 = {1, 3}. Write the given families of sets as a rosters.
(b) {Ai : i ∈ {2, 4}}
(c) {Ai : i = 1}
(d) {Ai : i = 1, 2}
(e) {Ai : i ∈ ∅}
(f) {Ai : i ∈ A5}
2. Answer true or false.
(a) 1 ∈ {{1}, {2}, {1, 2}}
(b) {1} ∈ {{1}, {2}, {1, 2}}
(c) {1} ⊆ {{1}, {2}, {1, 2}}
(d) {1, 2} ∈ {{{1, 2}, {3, 4}}, {1, 2}}
(e) {1, 2} ⊆ {{{1, 2}, {3, 4}}, {1, 2}}
(f) {3, 4} ∈ {{{1, 2}, {3, 4}}, {1, 2}}
(g) {3, 4} ⊆ {{{1, 2}, {3, 4}}, {1, 2}}
(h) ∅ ∈ {{{1, 2}, {3, 4}}, {1, 2}}
(i) ∅ ⊆ {{{1, 2}, {3, 4}}, {1, 2}}
(j) {∅} ∈ {∅, {∅, {∅}}}
(k) {∅} ⊆ {∅, {∅, {∅}}}
(l) ∅ ∈ {∅, {∅, {∅}}}
(m) ∅ ⊆ {∅, {∅, {∅}}}
(n) {∅} ⊆ ∅
(o) {∅} ⊆ {∅, {∅}}
(p) {∅} ⊆ {{∅, {∅}}}
(q) {{∅}} ⊆ {∅, {∅}}
(r) {1} ∈ P(Z)
(s) {1} ⊆ P(Z)
(t) ∅ ∈ P(∅)
(u) {∅} ∈ P(∅)
(v) {∅} ⊆ P(∅)
3. Find sets such that I ∩ J = ∅ but {Ai : i ∈ I} and {Aj : j ∈ J} are not disjoint.
4. Let {Ai : i ∈ K} be a family of sets and let I and J be subsets of K. Define ![]() = {Ai : i ∈ I} and
= {Ai : i ∈ I} and ![]() = {Aj : j ∈ J} and prove the following.
= {Aj : j ∈ J} and prove the following.
(a) If I ⊆ J, then ![]() ⊆
⊆ ![]() .
.
(b) ![]() ∪
∪ ![]() = {Ai : i ∈ I ∪ J}
= {Ai : i ∈ I ∪ J}
(c) {Ai : i ∈ I ∩ J} ⊆ ![]() ∩
∩ ![]()
5. Using the same notation as in the previous problem, find a family {Ai : i ∈ K} and subsets I and J of K such that:
(a) ![]() ∩
∩ ![]()
![]() {Ai : i ∈ I ∩ J}
{Ai : i ∈ I ∩ J}
(b) {Ai : i ∈ I J} ![]()
![]()
![]()
6. Show {Ai : i ∈ I} = ∅ if and only if I = ∅.
7. Let A be a finite set. How many elements are in P(A) if A has n elements? Explain.
8. Find the given power sets.
(a) P({1, 2})
(b) P(P({1, 2}))
(c) P(∅)
(d) P(P(∅))
(e) P({{∅}})
(f) P({∅, {∅}, {∅, {∅}}})
9. Prove Theorem 3.4.7.
10. For each of the given equalities, prove or show false. If one is false, prove any true inclusion.
(a) P(A ∪ B) = P(A) ∪ P(B)
(b) P(A ∩ B) = P(A) ∩ P(B)
(c) P(A B) = P(A) P(B)
(d) P(A × B) = P(A) × P(B)
11. Prove P(A) ⊆ P(B) implies A ⊆ B by using the fact that A ∈ P(A).
12. Write the following sets in roster form.
(a) ![]() {{1, 2}, {1, 2}, {1, 3}, {1, 4}}
{{1, 2}, {1, 2}, {1, 3}, {1, 4}}
(b) ![]() {{1, 2}, {1, 2}, {1, 3}, {1, 4}}
{{1, 2}, {1, 2}, {1, 3}, {1, 4}}
(c) ![]() P(∅)
P(∅)
(d) ![]() P(∅)
P(∅)
(e) ![]()
![]() {{{1}}, {{1, 2}}, {{1, 3}}, {{1, 4}}}
{{{1}}, {{1, 2}}, {{1, 3}}, {{1, 4}}}
(f) ![]()
![]() {{{1}}, {{1, 2}}, {{1, 3}}, {{1, 4}}}
{{{1}}, {{1, 2}}, {{1, 3}}, {{1, 4}}}
(g) ![]()
![]() {{{1}}, {{1, 2}}, {{1, 3}}, {{1, 4}}}
{{{1}}, {{1, 2}}, {{1, 3}}, {{1, 4}}}
(h) ![]()
![]() {{{1}}, {{1, 2}}, {{1, 3}}, {{1, 4}}}
{{{1}}, {{1, 2}}, {{1, 3}}, {{1, 4}}}
(i) ![]()
![]() ∅
∅
(j) ![]()
![]() ∅
∅
13. Draw Venn diagrams for a disjoint family of sets that is not pairwise disjoint and for a pairwise disjoint family of sets.
14. Show by example that a disjoint family of sets might not be pairwise disjoint.
15. Given a family of sets {Ai : i ∈ I}, find a family ![]() = {Bi : i ∈ I} such that {Ai × Bi : i ∈ I} is pairwise disjoint.
= {Bi : i ∈ I} such that {Ai × Bi : i ∈ I} is pairwise disjoint.
16. Let ![]() = {Ai : i ∈ I} be a family of sets. Prove the given equations.
= {Ai : i ∈ I} be a family of sets. Prove the given equations.
(a) ![]()
(b) ![]()
17. Prove for any sets A and B, ![]() {A, B} = A ∪ B and
{A, B} = A ∪ B and ![]() {A, B} = A ∩ B.
{A, B} = A ∩ B.
18. Let ![]() = {(0, n) : n ∈ Z+}. Prove that
= {(0, n) : n ∈ Z+}. Prove that ![]()
![]() = (0, ∞) and
= (0, ∞) and ![]()
![]() = (0, 1).
= (0, 1).
19. Prove the second part of Theorem 3.4.13.
20. Prove Theorem 3.4.17 indirectly.
21. Is Theorem 3.4.17 still true if the family of sets ![]() has at most one element? Explain.
has at most one element? Explain.
22. Let {Ai : i ∈ I} be a family of sets and prove the following.
(a) If B ⊆ Ai for some i ∈ I, then B ⊆ ![]() i∈I Ai.
i∈I Ai.
(b) If Ai ⊆ B for all i ∈ I, ![]() i∈I Ai ⊆ B.
i∈I Ai ⊆ B.
(c) If B ⊆ ![]() i∈I Ai, then B ⊆ Ai for all i ∈ I.
i∈I Ai, then B ⊆ Ai for all i ∈ I.
23. Prove Theorem 3.4.14.
24. Show ![]() ∅ = U where U is a universe.
∅ = U where U is a universe.
25. Let ![]() be a family of sets such that ∅ ∈
be a family of sets such that ∅ ∈ ![]() . Prove
. Prove ![]()
![]() = ∅.
= ∅.
26. Find families of sets ![]() and
and ![]() so that
so that ![]()
![]() =
= ![]()
![]() but
but ![]() ≠
≠ ![]() . Can this be repeated by replacing union with intersection?
. Can this be repeated by replacing union with intersection?
27. Let ![]() be a family of sets, and let A ∈
be a family of sets, and let A ∈ ![]() . Prove
. Prove ![]()
![]() ⊆ A ⊆
⊆ A ⊆ ![]()
![]() .
.
28. Let ![]() and
and ![]() be families of sets. Show the following.
be families of sets. Show the following.
(a) ![]() {
{![]() } =
} = ![]()
(b) ![]() {
{![]() } =
} = ![]()
(c) If ![]() ⊆
⊆ ![]() , then
, then ![]()
![]() ⊆
⊆ ![]()
![]() .
.
(d) If ![]() ⊆
⊆ ![]() , then
, then ![]()
![]() ⊆
⊆ ![]()
![]() .
.
(e) ![]() (
(![]() ∪
∪ ![]() ) =
) = ![]()
![]() ∪
∪ ![]()
![]()
(f) ![]() (
(![]() ∪
∪ ![]() ) =
) = ![]()
![]() ∩
∩ ![]()
![]()
29. Find families of sets ![]() and
and ![]() that make the following false.
that make the following false.
(a) ![]() (
(![]() ∩
∩ ![]() ) =
) = ![]()
![]() ∩
∩ ![]()
![]()
(b) ![]() (
(![]() ∩
∩ ![]() ) =
) = ![]()
![]() ∩
∩ ![]()
![]()
30. Let ![]() be a family of sets. For each of the given equalities, prove true or show that it is false by finding a counter-example.
be a family of sets. For each of the given equalities, prove true or show that it is false by finding a counter-example.
(a) ![]() P(
P(![]() ) =
) = ![]()
(b) ![]() P(
P(![]() ) =
) = ![]()
(c) P(![]()
![]() ) =
) = ![]()
(d) P(![]()
![]() ) =
) = ![]()
31. Prove these alternate forms of De Morgan's laws.
(a) A ![]() i∈I Bi =
i∈I Bi = ![]() i∈I A Bi
i∈I A Bi
(b) A ![]() i∈I Bi =
i∈I Bi = ![]() i∈I A Bi
i∈I A Bi
32. Assume that the universe U contains only sets such that for all A ∈ U, A ⊆ U and P(A) ∈ U. Prove the following equalities.
(a) ![]() U = U
U = U
(b) ![]() U = ∅
U = ∅
33. Let In = [n, n + 1] and Jn = [n, n + 1], n ∈ Z. Define
![]()
Show ![]()
![]() = R2 and
= R2 and ![]()
![]() = ∅. Is
= ∅. Is ![]() pairwise disjoint?
pairwise disjoint?








