8

Variations on a Theme by Gauss

The solving of an astronomical problem [proposed by the French Academy of Sciences in 1735], for which several eminent mathematicians had demanded several months’ time… was solved by the illustrious Gauss in one hour.

—Florian Cajori, quoted in R. E. Moritz, On Mathematics and Mathematicians, p. 155

There is a story about the great German mathematician Carl Friedrich Gauss (1777–1855), who as a schoolboy was asked by his teacher to sum up the numbers from 1 to 100, and who almost immediately came up with the correct answer, 5,050. To the amazed teacher Gauss explained that he had merely noticed that by writing the numbers twice, first from 1 to 100 and then from 100 to 1, and adding the two sums vertically, each pair adds up to 101. Since there are one hundred such pairs, we get 100 × 101 = 10,100, and since this is twice the required sum, the answer is one half of this, namely 5,050.

Like so many stories about famous people, this one may or may not have actually happened; however, what matters is the lesson to be drawn from it—the importance of looking for patterns. The pattern in this case is that of a staircase, where what we add at one end is subtracted at the other end:

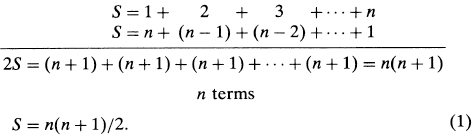
I remembered the story about Gauss while browsing one day through a handbook of sequences and series, where I found the following summation formula:¹

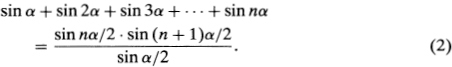
Not having at first any clue as to how to prove this formula, I began to look for a pattern. What struck me was the formal similarity between equations (1) and (2); indeed, multiplying both sides of equation (1) by α gives us Sα = n(n + l)α/2; that is,

α + 2α + 3α +···+ nα = n(n + l)α/2.

“Multiplying” this last equation by “sin” and proceeding as if “sin” were an ordinary algebraic quantity, we get

sin (α + 2α + 3α +···+ nα) = sin n(n + 1)α/2.

If on the left side we open the parentheses, and on the right side multiply and divide by a second “sin” (squeezing it between the n and (n + 1)) and again by α/2, we get equation (2)!

Of course, we have committed every imaginable mathematical sin (no pun intended), and yet we did get a correct formula. Can we, then, prove equation (2) in a manner similar to Gauss’s handling of the sum in equation (1)?

Let

Summing the terms vertically in pairs and using the sum-to-product formula sin α + sinβ = 2 sin (α + β)/2 · cos (α − β)/2, we get

To get rid of the bothersome 1/2,3/2,… appearing in the cosine terms, let us multiply the last equation by sin α/2 and use the product-to-sum formula sin α · cosβ = (l/2)[sin(α − β) + sin (α + β)]; we get

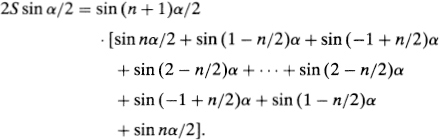
But sin(—1 + n/2)α = −sin(l − n/2)α, and similarly for the other terms; the expression in the brackets is therefore a “telescopic sum,” all of whose terms except the first and last (which are equal) cancel out. We thus have

2S sin α/2 = 2 sin (n + l)α/2 · sin nα/2

or

which is the formula we wished to prove.

An analogous formula for the summation of cosines can be proved in a similar way:²

If we now divide equation (2) by equation (3), we get the beautiful formula

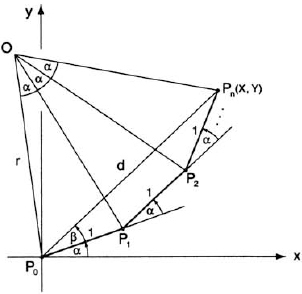
But this is not the end of the story. Following the idea that every trigonometric formula ultimately derives from geometry, we turn to fig. 51. Starting at the origin (which for our purpose we have labeled as P₀), we draw a line segment P₀P₁ of unit length forming an angle α with the positive x-axis. At P₁ we draw a second line segment of unit length forming an angle α with the first segment and therefore the angle 2α with the x-axis. Continuing in this manner n times, we arrive at the point P_n, whose coordinates we shall denote by X and Y. Clearly X is the sum of the horizontal projections of the n line segments, and Y is the sum of their vertical projections, so we have

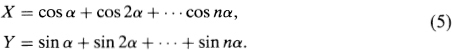
FIG. 51. Geometric construction of the sum S = sin α + sin 2α + ···+ sin nα

Now the points P_i lie on a regular polygon inscribed in a circle with center O and radius r. Each line segment P_i−1P_i subtends an angle α at O, and thus the segment P₀P_n subtends the angle (nα) at O. But this segment is the diagonal connecting the points P₀ and P_n; let us denote its length by d. In the isosceles triangle P₀OP_n we have

d = 2r sin nα/2,

while in the isosceles triangle P₀OP₁ we have

1 = 2r sin α/2.

Eliminating r between these two equations, we get

In order to find the horizontal and vertical projections of the segment P₀P_n, we need to find the angle it forms with the x-axis. This angle is (α + β), where β = ∠P₁P₀P_n. Now angle β subtends the chord P₁P_n in the inscribing circle and is therefore equal to half the central angle that subtends the same chord, that is, to (n − l)α/2. Thus α + β = α + (n − 1)α/2 = (n + l)α/2. Hence

If we substitute the expressions for X and Y from equations (5) into equations (6), we get equations (2) and (3).

If we think of each line segment P_i−1P_i as a vector from P_i−1 to P_i then the line segment P₀P_n is their vector sum. Equations (2) and (3) then say that the sum of the (vertical or horizontal) projections of the individual line segments equals the (vertical or horizontal) projection of their vector sum. This shows that projection is a linear operation—an operation that obeys the distributive law p(u + v) = p(u) + p(v), where p( ) stands for “projection of” and u and v are any two vectors. Projection—like all linear operations—behaves exactly as ordinary multiplication.

We can use “Gauss’s method” of summation to prove other trigonometric summation formulas. Here are a few examples:

The last two are special cases of equations (3) and (8), respectively; they are remarkable because the sum in each is independent of n.

Trigonometric sums were studied by the Hungarian mathematician Lipót Fejér (1880–1959) in connection with his work on the summation of Fourier series, a subject to which we will return in chapter 15.

NOTES AND SOURCES

1. Summation of Series, collected by L.B.W. Jolley (1925; rpt. New York: Dover, 1961), series no. 417.

2. Both formulas can also be proved by taking the real and imaginary parts of the sum of the geometric progression e^iα + e^2iα + ··· + e^niα, where i = √−l; see Richard Courant, Differential and Integral Calculus (1934; rpt. London: Blackie & Son, 1956), vol. 1, p. 436.