Recreational Mathematics in Ancient Egypt
Problem 79 of the Rhind Papyrus says (fig. 3):1

a The Egyptian word for “cat” is myw; when the missing vowels are inserted, this becomes meey’auw.
b Obviously Ahmes made a mistake here. The correct entry should be 2,401.
What is the meaning behind this cryptic verse? Clearly we have before us a geometric progression whose initial term and common ratio are both 7, and the scribe shows us how to find its sum. But as any good teacher would do to break the monotony of a routine math class, Ahmes embellishes the exercise with a little story which might be read like this: There are seven houses; in each house there are seven cats; each cat eats seven mice; each mouse eats seven ears of spelt; each ear of spelt produces seven hekat of grain. Find the total number of items involved.
The right hand column clearly gives the terms of the progression 7, 72, 73, 74, 75 followed by their sum, 19,607 (whether the mistaken entry 2,301 was Ahmes’s own error in copying or whether it had already been in the original document, we shall never know). But now Ahmes plays his second card: in the left-hand column he shows us how to obtain the answer in a shorter, “clever” way; and in following it we can see the Egyptian method of multiplication at work. The Egyptians knew that any integer can be represented as a sum of terms of the geometric progression 1,2,4,8,…, and that the representation is unique (this is precisely the representation of an integer in terms of the base 2, the coefficients, or “binary digits,” being 0 and 1). To multiply, say, 13 by 17, they only had to write one of the multipliers, say 13, as a sum of powers of 2, 13 = 1 + 4 + 8, multiply each power by the other multiplier, and add the results: 13 × 17 = 1 × 17 + 4 × 17 + 8 × 17 = 17 + 68 + 136 = 221. The work can be conveniently done in a tabular form:

FIG. 3. Problem 79 of the Rhind Papyrus.
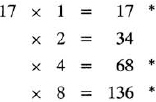
The astrisks indicate the powers to be added. Thus the Egyptians could do any multiplication by repeated doubling and adding. In all the Egyptian mathematical writings known to us, this practice is always followed; it was as basic to the Egyptian scribe as the multiplication table is to a pupil today.
So where does 2,801, the first number in the left-hand column of Problem 79, come from? Here Ahmes uses a property of geometric progressions with which the Egyptians were familiar: the sum of the first n terms of a geometric progression with the same initial term and common ratio is equal to the common ratio multiplied by one plus the sum of the first (n − 1) terms; in modern notation, a + a2 + a3 +… + an = a(l + a + a2 +… + an−l). This sort of “recursion formula” enabled the Egyptian scribe to reduce the summation of one geometric progression to that of another one with fewer (and smaller) terms. To find the sum of the progression 7 + 49 + 343 + 2,401 + 16,807, Ahmes thought of it as 7 × (1 + 7 + 49 + 343 + 2,401); since the sum of the terms inside the parentheses is 2,801, all he had to do was to multiply this number by 7, thinking of 7 as 1 + 2 + 4. This is what the left-hand column shows us. Note that this column requires only three steps, compared to the five steps of the “obvious” solution shown in the right-hand column; clearly the scribe included this exercise as an example in creative thinking.
One may ask: why did Ahmes choose the common ratio 7? In his excellent book, Mathematics in the Times of the Pharaohs, Richard J. Gillings answers this question as follows: “The number 7 often presents itself in Egyptian multiplication because, by regular doubling, the first three multipliers are always 1, 2, 4, which add to 7.”2 This explanation, however, is somewhat unconvincing, for it would equally apply to 3 (= 1 + 2), to 15 ( = 1 + 2 + 4 + 8), and in fact to all integers of the form 2n − 1. A more plausible explanation might be that 7 was chosen because a larger number would have made the calculation too long, while a smaller one would not have illustrated the rapid growth of the progression: had Ahmes used 3, the final answer (363) may not have been “sensational” enough to impress the reader.
The dramatic growth of a geometric progression has fascinated mathematicians throughout the ages; it even found its way into the folklore of some cultures. An old legend has it that the king of Persia was so impressed by the game of chess that he wished to reward its inventor. When summoned to the royal palace, the inventor, a poor peasant from a remote corner of the kingdom, merely requested that one grain of wheat be put on the first square of the chessboard, two grains on the second square, four grains on the third, and so on until all 64 squares were covered. Surprised by the modesty of this request, the king ordered his servants to bring a few bags of wheat, and they patiently began to put the grains on the board. It soon became clear, however, that not even the entire amount of grain in the kingdom sufficed to fulfill the request, for the sum of the progression 1 + 2 + 22 +… + 263 is a staggering 18,446,744,073,709,551,615—enough to form a line of grain some two light years long!
Ahmes’s Problem 79 has a strong likeness to an old nursery rhyme:
As I was going to St. Ives,
I met a man with seven wives;
Every wife had seven sacks,
Every sack had seven cats,
Every cat had seven kits.
Kits, cats, sacks and wives,
How many were going to St. Ives?
In Leonardo Pisano’s (“Fibonacci”) famous work Liber Abaci (1202) there is a problem which, except for the story involved, is identical to this rhyme. This has led some scholars to suggest that Problem 79 “has perpetuated itself through all the centuries from the times of the ancient Egyptians.”3 To which Gillings replies: “All the available evidence for this [conclusion] is here before us, and one is entitled to draw whatever conclusions one wishes. It is indeed tempting to be able to say to a child, ‘Here is a nursery rhyme that is nearly 4,000 years old!’ But is it really? We shall never truly know.”4
Geometric progressions may seem quite removed from trigonometry, but in chapter 9 we will show that the two are indeed closely related. This will allow us to investigate these progressions geometrically and perhaps justify the adjective “geometric” that has, for no apparent reason, been associated with them.
NOTES AND SOURCES
1. Arnold Buffum Chace, The Rhind Mathematical Papyrus: Free Translation and Commentary with Selected Photographs, Transcriptions, Transliterations and Literal Translations (Reston, Va.: National Council of Teachers of Mathematics, 1979), p. 136. I have used here Chace’s literal (rather than free) translation in order to preserve the flavor and charm of the problem as originally stated. This also includes Ahmes’s obvious error in the fourth line of the right column. For Chace’s free translation, see p. 59 of his book.
2. Richard J. Gillings, Mathematics in the Times of the Pharoahs. (1972; rpt. New York: Dover, 1982), p. 168.
3. L. Rodet as quoted by Chace, Rhind Mathematical Papyrus, p. 59.
4. Gillings, Mathematics, p. 170.
