9

Had Zeno Only Known This!

One, Two, Three—Infinity

—Title of a book by George Gamow

Can space be endlessly divided, or is there a smallest unit of space, a mathematical atom that cannot further be split? Is motion continuous, or is it but a succession of snapshots which, like the frames in an old motion picture, are themselves frozen in time? Questions such as these were hotly debated by the philosophers of ancient Greece, and they are still being debated today—witness the never-ending search for the ultimate elementary particle, that elusive building block from which all matter is supposedly made.

The Greek philosopher Zeno of Elea, who lived in the fifth century B.C., summarized these questions in four paradoxes—he called them “arguments”—whose purpose was to demonstrate the fundamental difficulties inherent in the notion of continuity. In one of these paradoxes, known as the “dichotomy,” he purports to show that motion is impossible: in order for a runner to go from point A to point B, he must first cover half the distance between A and B, then half the remaining distance, then half of that, and so on, ad infinitum (fig. 52). Since this involves an infinite number of steps, Zeno argued, the runner will never reach his destination.¹

It is easy to formulate Zeno’s paradox in modern terms. Let the distance from A to B be 1; by first covering half this distance, then half of what remains, and so on, the runner will cover a total distance given by the sum

1/2 + 1/4 + 1/8 + 1/16 + ···.

This sum is an endless geometric progression, or series, with the common ratio 1/2. As we add more and more terms, the sum keeps growing and approaches 1. It will never reach 1, let alone exceed 1; yet we can make the sum get as close to 1 as we please by simply adding more and more terms. In modern language, the sum approaches the limit 1 as the number of terms grows beyond bound. Thus the total distance covered is exactly 1; and since the time intervals it takes the runner to cover the partial distances (assuming he maintains a constant speed) also follow the same progression, he will cover the entire distance in finite time. This settles the “paradox.”

FIG. 52. The runner’s paradox.

The Greeks, however, did not subscribe to this kind of reasoning. They could not accept the fact—so obvious to us today—that a sum of infinitely many numbers may have a finite value. They had no difficulty adding up as many terms of a progression as were necessary to achieve a desired accuracy, but the thought of extending this process to infinity caused them great intellectual anguish. This in turn led to their horror infiniti—their fear of the infinite. Unable to deal with it, the Greeks barred infinity from their mathematical system. Although they had a firm intuitive grasp of the limit concept—as evidenced by Archimedes’ quadrature of the parabola—they recoiled at the thought of going all the way to infinity.² As a result, Zeno’s paradoxes remained a source of irritation and embarrassment to generations of scholars. Frustrated by their failure to resolve the paradoxes satisfactorily, they turned to philosophical and even metaphysical reasoning, thereby confusing the issue even further.³

There is hardly a branch of mathematics where geometric progressions—finite or infinite—do not play a role. We first encounter them in arithmetic in the form of repeating decimals, which are but infinite geometric progressions in disguise; for example, the repeating decimal 0.1212… is merely an abbreviation for the infinite series 12/100 + 12/100² + 12/100³ + ···. Geometric progressions are at the heart of most financial calculations, a result of the fact that money invested at a fixed interest rate grows geometrically with time. In calculus we are introduced to power series, and the simplest power series is the infinite geometric progression 1 + x + x² + ···, often used to test the convergence of other series. Archimedes of Syracuse (ca. 287–212 B.C.) cleverly used a geometric progression to find the area of a parabolic segment—one of the first quadratures of a curved shape.⁴ And the fractals of modern vintage, those intricate self-replicating curves that meander endlessly hither and thither, are but an application of the principle of self-similarity, of which the geometric progression is the simplest case (fig. 53). The Dutch artist Maurits C. Escher (1898–1972), whose mathematical drawings have intrigued a whole generation of scientists, used geometric progressions in several of his prints; we show here one of them, entitled Smaller and Smaller (Fig. 54).

A common misconception among students of mathematics (undoubtedly fueled by erroneous statements found in popular books) is that Euclid’s great work, the Elements, deals only with geometry. True, geometry occupies the bulk of the work, but it also contains an extensive treatment of arithmetic, number theory, and the theory of progressions. All of Book VIII and parts of Book IX are devoted to “continued proportions,” that is, numbers that form a geometric progression (a favorite subject with the Greeks ever since Pythagoras’s discovery that musical intervals correspond to simple proportions of string lengths). Proposition 35 of Book IX states in words how to find the sum of a geometric progression:

FIG, 53. Construction of the snowflake curve: start with an equilateral triangle, construct a smaller equilateral triangle over the middle third of each side, and cut the middle third to obtain a Star of David-like figure. Repeat the process with the new figure to get a 48-sided figure. Continuing in this manner, we get a sequence of shapes that, in the limit, approach a crinkly curve known as the snowflake curve (also called the Koch curve after its discoverer, the Swedish mathematician Helge von Koch [1870–1924]). The perimeter and area of these shapes follow geometric progressions with common ratios 4/3 and 4/9, respectively. Since these ratios are, respectively, greater than and less than 1, the perimeter tends to infinity, while the area tends to 8/5 the area of the original triangle. The snowflake curve was the first known “pathological curve”; it is nowhere smooth and hence has nowhere a derivative. Today such self-replicating shapes are called fractals.

If as many numbers as we please be in continued proportion, and there be subtracted from the second [number] and the last [number] numbers equal to the first, then, as the excess of the second is to the first, so will the excess of the last be to all those before it.

Translated into modern language, if the terms of the progression are a, ar, ar²,…, arⁿ and the sum of “all those before it” is S, then (ar − a) : a = (arⁿ − a) : S; cross-multiplying and simplifying, we get the familiar formula for the sum of the first n terms of a geometric progression,

FIG. 54. M. C. Escher’s Smaller and Smaller (1956). ©1997 Cordon-Art-Baarn-Holland. All rights reserved.

Euclid then uses this result to prove (Proposition 36 of Book IX) an elegant property of numbers: if the sum of the progression 1 + 2 + 2² +···+ 2ⁿ⁻¹ is a prime number, then the product of this prime and 2ⁿ⁻¹ is a perfect number. A positive integer N is perfect if it is the sum of its positive divisors other than N; the first two perfect numbers are 6 = 1 + 2 + 3 and 28 = 1 + 2 + 4 + 7 + 14. Since the sum of the progression 1 + 2 + 2² +···+ 2ⁿ⁻¹ is 2ⁿ−1, the proposition says that 2ⁿ⁻¹.(2ⁿ−1) is perfect whenever 2ⁿ−1 is prime. Thus 6 is perfect because 6 = 2·3 = 2²⁻¹ · (2²−1) and 28 is perfect because 28 = 4 · 7 = 2³⁻¹. (2³−1). The next two perfect numbers are 496 = 16 · 31 = 2⁵⁻¹. (2⁵−1) and 8,128 = 64 · 127 = 2^7−l · (2⁷−1). These four were the only perfect numbers known to the Greeks.⁶

And this is as far as the Greeks went. They made effective use of equation (1) in their development of geometry and number theory, allowing n to be arbitrarily large (“as many numbers as we please”); but they did not make the crucial step of actually letting n grow beyond all bounds—letting it tend to infinity. Had they not limited themselves with this self-imposed taboo, they just might have anticipated the discovery of the calculus by two thousand years.⁷

Today, with the limit concept firmly established, we have no qualms arguing that if r is a number whose absolute value is less than 1 (—1 < r < 1), then as n → ∞, the term rⁿ in equation (1) tends to zero, so that in the limit we get S = −a/(r − 1), or equivalently

which is the familiar formula for the sum of an infinite geometric progression.⁸ Thus the series in Zeno’s paradox, 1/2 +1/4 + 1/8 + 1/16 + ···, has the sum (l/2)/(l − 1/2) = 1, and the repeating decimal 0.1212 ··· = 12/100 + 12/10,000 + ··· has the sum (12/100)/(1 − 1/100) = 12/99 = 4/33. We can actually use equation (2) to prove that every repeating decimal is equal to some fraction, i.e., a rational number.

And now trigonometry enters the picture. We will show that every infinite geometric progression can be constructed geometrically, and its sum found graphically, using only a straightedge and compass.⁹ Our starting point is the fact that the sum of an infinite geometric progression with common ratio r converges to a limit if and only if − 1 < r < 1. Now any number between −1 and 1 is the cosine of exactly one angle between 0° and 180°; for example, 0.5 is the cosine of 60°, and −0.707 (more precisely, −√2/2) is the cosine of 135°. (Note that this is not so with the sine function: there are two angles, 30° and (180° − 30°) = 150°, whose sine is 0.5, and no angle between 0° and 180° whose sine is −0.707). Let us, therefore, write r = cos α, or conversely α = cos⁻¹ r, and regard the angle α as given.

On the x-axis let the origin be at P₀ and the point x = 1 at P₁ (fig. 55). At P₁ we draw a ray forming the angle α with the positive x-axis, and along it mark a segment P₁Q₁ of unit length. From Q₁ we drop a perpendicular to the x-axis, meeting it as P₂; we have P₁P₂ = 1 · cos α = cos α and thus P₀P₂ = 1 + cos α. We now repeat the process: at P₂ we draw a ray forming the angle α with the positive x-axis and along it mark a segment P₂Q₂ equal in length to P₁P₂ (using a compass centered at P₂ and opened to the length P₁P₂). From Q₂ we drop a perpendicular to the x-axis, meeting it at P₃; we have P₂P₃ = cos α · cos α = cos²α and thus P₀P₃ = 1 + cos α + cos² α. Continuing in this manner, it seems at first that we would have to repeat the process infinitely many times. But, as we will now show, the first two steps are sufficient to determine the sum of the entire series.

FIG. 55. Geometric construction of the series
S = 1 + cos α + cos² α +···.

First, the right triangles P₁Q₁P₂, P₂Q₂P₃, and so on are similar, having the same angle α; consequently the points Q₁, Q₂, ··· must lie on a straight line m. We claim that the point of intersection of m with the x-axis marks the sum S of the entire series, and we accordingly denote this point P_∞. To prove this, we note that the segments P₁Q₁ = 1, P₂Q₂ = cos α, P₃Q₃ = cos² α, and so on form a geometric progression with the common ratio cos α (the same as in the original progression). Going one step backward in this progression, we have P₀Q₀ = 1/cos α = sec α. Now the oblique triangles P₀Q₀P_∞, P₁Q₁P_∞, ··· are all similar; taking the first two of these triangles, we have P₀P_∞/P₀Q₀ = P₁P_∞/P₁Q₁ or

Changing the factor 1/sec α back to cos α and solving the equation for S, we get S = 1/(1 − cos α) = 1/(1 − r), showing that the segment P₀P_∞ is the sum of the entire series. We repeat: it is sufficient to construct the first two points Q₁ and Q₂; these determine the line m, whose intersection with the x-axis determines the point P_∞.

Not only does this construction provide a geometric interpretation of the geometric series, it also allows us to see what happens when we vary the common ratio r. Figures 56 and 57 show the construction for α = 60° and 45°, for which r = 1/2 and √2/2, respectively; the corresponding sums are 1/(1 − 1/2) = 2 and 1/(1 – √2/2) = 2 + √2 ≈ 3.414. As we vary r and with it a, points P₀ and P₁ remain fixed, but all other points will move along their respective lines. For α = 90° (that is, r = 0),Q₁ will be exactly above P₁ so that dropping the perpendicular from it to the x-axis brings us back to P₁: the series will not progress any further, and its sum is S = P₀P₁ = 1. As we decrease α from 90° to 0°, the line m becomes less and less steep; at the same time, points P₂,P₃,··· move to the right, and so does P_∞: the sum of the series becomes larger. As α → 0°, the line m becomes horizontal, and its point of intersection with the x-axis recedes to infinity: the series diverges.

FIG. 56. The construction for α = 60°.

If the common ratio r is negative, α will be between 90° and 180”. Starting again at P₁ (fig. 58), we draw a ray making with the positive x-axis the (obtuse) angle α; this brings us to point Q₁, with P₁Q₁ = 1. We now drop a perpendicular from Q₁ to the x-axis, meeting it at P₂ (note that P₂ is now to the left of P₁); we have P₁P₂ = cos α (a negative number) and thus P₀P₂ = 1 + cos α. From P₂ we draw a ray forming the angle α with the positive x-axis; note that since segment P₁P₂ is directed to the left, the ray will be directed downward. On this ray we mark off a segment P₂Q₂ equal in length to P₁P₂. From Q₂ we drop a perpendicular to the x-axis, meeting it at P₃ (note that P₃ is to the right of P₂); we have P₂P₃ = cos²α (a positive number), hence P₀P₃ = 1 + cos α + cos² α. Proceeding in this way, we get ever smaller right triangles, each nested within the one preceding it by two steps. All these triangles are similar.

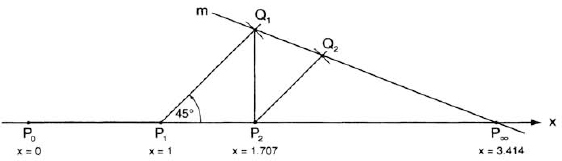
FIG. 57. The construction for α = 45°.

FIG. 58. The case when α is obtuse.

It follows, as before, that the points Q₁, Q₂, ··· lie on a straight line m, whose point of intersection with the x-axis gives us the sum of the entire series. Denoting this point by P_∞, we note that it lies to the right of the points P_2n and to the left of the points P_2n+1: the series approaches its sum alternately from above and below, depending on whether we have summed up an odd or an even number of terms. Figures 59 and 60 show the construction for α = 120° and 150° (that is, r = −1/2 and −√3/2, respectively), for which the series converges to 1/(1 + 1/2) = 2/3 ≈ 0.666 and 1/(1 + √3/2) ≈ 0.536.

Now let us once again vary the angle α, this time increasing it from 90° to 180°. The line m will assume a less and less steep position, with, however, a negative slope. At the same time the points P_2n will move to the left toward P₀, while the points P_2n+1 will move to the right toward P₁. As α → 180° (that is, as r → −1), the points Q_2n+1 will cluster above P₀ and the points Q_2n will cluster below P₁, so that the line m will assume a nearly symmetrical position relative to the segment P₀P₁, intersecting it just to the right of the point x = 1/2, And this, indeed, is the value to which the formula S = 1/(1 − r) tends as r → −1. At the same time, however, the points P_2n will crowd about P₀ (that is, about x = 0), while the points P_2n+1 will crowd about P₁ (x = 1), showing that the series will tend to oscillate between 0 and 1.

FIG. 59. The construction for α = 120°.

FIG. 60. The construction for α = 150°.

When α = 180° (that is, r = −1) the situation suddenly changes, for then all the points Q_2n+1 merge with P₀ (as also the points P_2n), while the points Q_2n merge with P₁ The line m will then merge with the x-axis, intersecting it at infinitely many points, and it becomes impossible to determine the point P_∞. At first this situation seems contradictory, since for α = 180° our series becomes 1 − 1 + 1 − 1 + − ···, whose partial sums oscillate between 0 and 1. But this is not so! The series can actually be made to equal any arbitrary number, which merely shows that the series does not converge and its sum has no meaning.¹⁰

The seemingly bizarre behavior of the series 1 − 1 + 1 − 1 + − ··· aroused much controversy in the early eighteenth century. Gottfried Wilhelm Leibniz (1646–1716), co-inventor with Newton of the calculus, argued that since the sum may be 0 or 1 with equal probability, its “true” value should be their mean, namely 1/2, in agreement with the formula S = 1/(1 − r) when r = −1. Such careless reasoning may seem incredible to us today, but in Leibniz’s time the concepts of convergence and limit were not yet understood, and infinite series were treated in a purely manipulative manner, as if they were an extension of ordinary finite sums.

As he groped with this series, Leibniz—who was a philosopher at heart—must have thought of Zeno, his predecessor by two thousand years. Had Zeno been aware of our construction, perhaps it might have made it easier for him to accept the fact that an infinite sum of numbers may be finite. And the consequences would have been profound, for had the Greeks not been so stubborn in barring infinity from their world, the course of mathematics might have been forever changed.

NOTES AND SOURCES

1. A variation of the paradox says that for the runner to go from A to B he must first reach the midpoint C between A and B; but in order to reach C, he must first reach the midpoint D between A and C, and so on.

2. For the causes of this fear, see my book, e: The Story of a Number (Princeton, N.J.: Princeton University Press, 1994), pp. 43–47.

3. Even today some thinkers refuse to regard Zeno’s paradoxes as settled; see the articles “Resolving Zeno’s Paradoxes” by William I. McLaughlin, Scientific American, November 1994, and “A Brief History of Infinity” by A. W. Moore, Scientific American, April 1995. See also Adolf Grünbaum, Modern Science and Zeno’s Paradoxes (Middletown, Conn.: Wesleyan University Press, 1967).

4. See the chapter “Quadrature of the Parabola” in Thomas L. Heath, The Works of Archimedes (1897; rpt. New York: Dover, 1953).

5. A modern proof is to write S = a + ar + ar² +···+ ar^n−l, multiply this equation by r, and subtract the result from the original equation: all terms except the first and last will cancel, giving us (1 − r)S = a − arⁿ, from which we get S = a(l − rⁿ)/(l − r) = a(rⁿ − l)/(r − 1).

6. Note that 2ⁿ − 1 is not prime for every prime n; for example, 2¹¹ − 1 = 2047 = 23 · 89 is composite, and therefore 2¹¹⁻¹ · (2¹¹ − 1) = 2,096,128 is not perfect. Primes of the form 2ⁿ − 1 where n is prime are called Mersenne primes, named after Marin Mersenne (1588–1648), the French friar of the order of Minims; as of 1996 only thirty-four Mersenne primes were known, the largest being 2^1,257,787 − 1, a 378,632-digit number discovered in that year. Because every Mersenne prime generates a perfect number, their histories are closely related.

By necessity, the formula 2^n−l · (2ⁿ−1) produces only even perfect numbers. In 1770 Leonhard Euler proved the converse of Proposition 36: Every even perfect number must be of the form 2ⁿ−1 · (2ⁿ − 1), where 2ⁿ − 1 is prime. It is not known whether odd perfect numbers exist, nor whether the number of perfect numbers is finite or infinite. For further details, see any good book on number theory.

7. See Heath, Works of Archimedes, chap.7, “Anticipations by Archimedes of the Integral Calculus”.

8. A common (though not quite rigorous) proof of equation (2) is to write S = a + ar + ar² + ar³ +··· = a + r(a + ar + ar² +···) = a + rS, from which we get S(1 − r) − a or S = a/(l − r).

9. The subsequent material is based on my article “Geometric Construction of the Geometric Series” in the International Journal of Mathematics Education in Science and Technology, vol. 8, no. 1 (January 1977), pp. 89–96.

10. To show this, let a and b be any two numbers such that a + b = 1. Our series then becomes (a + b) − (a + b) + (a + b) − (a + b) +···. Let us call its sum S. Shifting the parentheses one position to the right, we obtain the series S = a + (b − a) − (b − a) + (b − a) − (b − a) +···. Now put b − a = c. Then S = a + c − c + c − c+−···. We can sum this last series in two ways, depending on how we arrange the parentheses: S = a + (c − c) + (c − c) + (c − c) +··· = a, or S = a + c − (c − c) − (c − c) − (c − c) − ··· = a + c = a + (b − a) = b. Thus the series can have either α or b as its sum, and as the splitting of 1 into α and b was entirely arbitrary, S can have any value whatsoever. This, of course, merely shows that the partial sums do not converge to a fixed value, and thus the series diverges (though not to infinity).