6

Two Theorems from Geometry

It is the glory of geometry that from so few principles, fetched from without, it is able to accomplish so much.

—Sir Isaac Newton, preface to the Principia

Proposition 20 of Book III of Euclid’s Elements says:

In a circle the angle at the center is double of the angle at the circumference, when the angles have the same circumference as base.¹

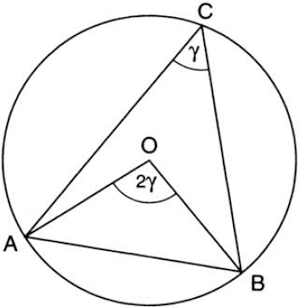
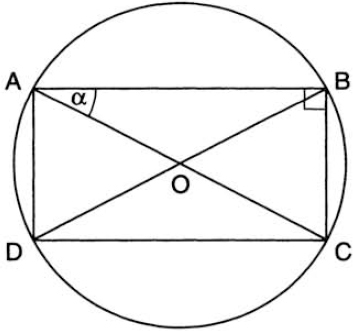
In more common language, the proposition says that an angle inscribed in a circle (that is, an angle whose vertex lies on the circumference) is equal to half the central angle that subtends the same chord (fig. 28). Two corollaries from this theorem immediately follow: (1) In a given circle, all inscribed angles subtending the same chord are equal (this is Proposition 21 of Euclid; see fig. 29); and (2) All inscribed angles subtending the diameter are right angles (fig. 30). This last result is said to have been proved by Thales (although the Babylonians had already known it a thousand years before him) and may be one of the earliest theorems ever to have been proved.

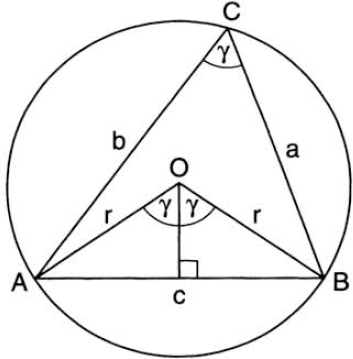
This simple theorem, with its two corollaries, is a treasure trove of trigonometric information, and we will have numerous occasions to use it throughout this book. Let us use it here to prove the Law of Sines. Figure 31 shows a triangle ABC inscribed in a circle with center at O and radius r. We have ∠AOB = 2∠ACB = 2γ. Drop the perpendicular bisector from O to AB. Then sin γ = (c/2)/r, hence c/sin γ = 2r = constant. Since the ratio c/sin γ is constant (i.e., has the same value regardless of c and γ), we have

Not only is this proof a model of simplicity, it also gives the sine law in its complete form; the more common proof, based on dissecting a triangle into two right triangles, entirely ignores the statement about 2r.

FIG. 28. Propositon 20 of Book III of Euclid’s Elements.

FIG. 29. Proposition 21 of Book III of Euclid’s Elements.

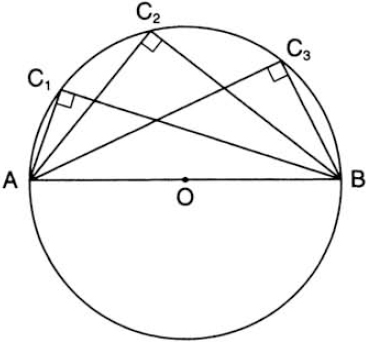
FIG. 30. All inscribed angles subtending a diameter are right angles.

FIG. 31. The Law of Sines: the acute case.

In figure 31 the angle γ is acute, which means that the center of the circle lies inside the triangle. If γ is obtuse (fig. 32), the center lies outside, so that arc AB is greater than half the circumference. Thus the internal angle of triangle AOB at O is γ′ = 360° − 2γ. Again drop the perpendicular bisector from O to AB: we have sin γ′/2 = (c/2)/r. But sin γ′/2 = sin (180° − γ) = sin γ, so we again get c/sin γ = 2r, as before.

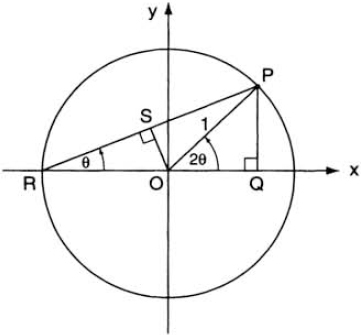
We can get still more information out of our theorem. Figure 33 shows the unit circle and a point P on it. Let the angle between OP and the positive x-axis be 2θ. Then ∠ORP = θ, where R is the point with coordinates (−1, 0). Applying the sine law to the triangle ORP, we have RP/sin (180° − 2θ) = OP/sin θ. But sin(180° − 2θ) = sin 2θ and OP = 1, so RP/sin 2θ = 1/sin θ, from which we get

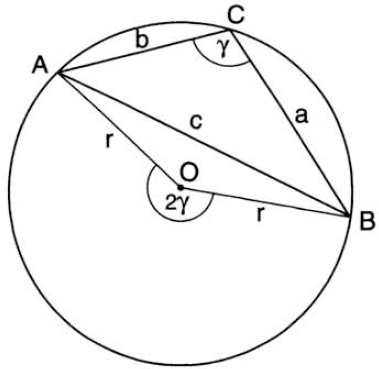
FIG. 32. The Law of Sines: the obtuse case.

FIG. 33. Geometric proof of the double-angle formulas.

Now drop the perpendicular bisector OS from O to RP; in the right triangle ORS we have cos θ = RS/RO = (RP/2)/RO = RP/2, hence RP = 2 cos θ. Substituting this back in equation (2), we get

which is the double-angle formula for the sine. Again, dropping the perpendicular PQ from P to the x-axis, we have

which is the double-angle formula for the cosine. Finally, having proved the double-angle formulas, we can derive the corresponding half-angle formulas by simply replacing 2θ by ϕ.

Let us return for a moment to our proof of the Law of Sines. Since any three noncollinear points determine a circle uniquely, every triangle can be inscribed in exactly one circle. Indeed, we may regard the angles of the triangle as inscribed angles and the sides as chords in that circle. Thus the Law of Sines is really a theorem about circles. If we let the diameter of the inscribing circle be 1 and call this circle the “unit circle,” then the Law of Sines simply says that

a = sin α, b = sin β, c = sin γ,

that is, each side of a triangle inscribed in a unit circle is equal to the sine of the opposite angle (fig. 34). We could, in fact, define the sine of an angle as the length of the chord it subtends in the unit circle, and this definition would be as good as the traditional definition of the sine as a ratio of two sides in a right triangle. (It would, in fact, have the advantage that the angle could vary from 0° to 180°—twice the range in a right triangle.) As we saw in chapter 2, it was this interpretation of the sine function that Ptolemy used in his table of chords.

FIG. 34. The Law of Sines in a “unit circle.”

In Ptolemy’s Almagest we find the following proposition, known as Ptolemy’s Theorem:²

The rectangle contained by the diagonals of any quadrilateral inscribed in a circle is equal to the sum of the rectangles contained by the pairs of opposite sides.³

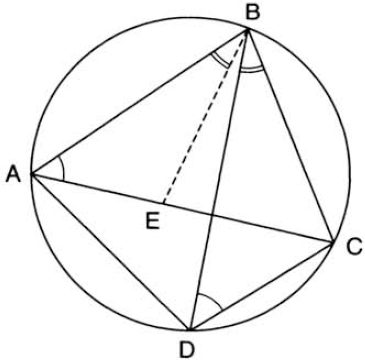
What is the meaning of this cryptic statement? To begin with, the Greeks interpreted a number as the length of a line segment, and the product of two numbers as the area of a rectangle with sides having the given numbers as lengths. Thus “the rectangle contained by the diagonals” means the area of a rectangle whose sides are the diagonals of an inscribed quadrilateral, with a similar interpretation for “the rectangles contained by the pairs of opposite sides.” In short, “a rectangle contained by” simply means “a product of.” Ptolemy’s Theorem can then be formulated as follows: In a quadrilateral inscribed in a circle, the product of the diagonals is equal to the sum of the products of the opposite sides. Referring to figure 35, this means that

As this theorem is not as widely known as others in elementary geometry, we give here Ptolemy’s proof: Using one side, say AB, as the initial side, we construct an angle ABE equal to DBC. Now angles CAB and CDB are also equal, having the common chord BC. Therefore, triangles ABE and DBC are similar, having two pairs of equai angles. Hence AE/AB = DC/DB, from which we get

FIG. 35. Ptolemy’s Theorem.

If we now add the angle EBD to both sides of the equation ∠ABE = ∠DBC, we get ∠ABD = ∠EBC. But angles BDA and BCE are also equal, having the common chord AB. Therefore, triangles ABD and EBC are similar, hence AD/DB = EC/CB and thus

Finally, adding equations (6) and (7), we have (AE + EC) · DB = AB · DC + AD · CB; replacing AE + EC by AC, we get the required result (note that the sides are nondirected line segments, so that BD = DB, etc.).

If we let the quadrilateral ABCD be a rectangle (fig. 36), then all four vertices form right angles, and furthermore AB = CD, BC = DA, and AC = BD. Equation (5) then says that

which is the Pythagorean Theorem! This demonstration of the most celebrated theorem of mathematics appears as number 66 of 256 proofs in Elisha Scott Loomis’s classic book, The Pythagorean Proposition.⁴

What is the trigonometric significance of Ptolemy’s Theorem? For the special case where ABCD is a rectangle, AC is a diameter in our “unit circle,” hence AC = 1. Moreover, denoting angle BAC by α, we have AB = cos α, BC = sin α. Equation (8) thus becomes

FIG. 36. The Pythagorean Theorem.

1 = cos² α + sin² α,

which is the trigonometric equivalent of the Pythagorean Theorem. But there is more in store. Let ABCD be any quadrilateral in which one diagonal, say AC, coincides with the diameter (fig. 37). Then ∠ABC and ∠ADC are right angles. Let ∠BAC = α, ∠CAD = β. We then have BC = sin α, AB = cos α, CD = sin β, AD = cos β, and BD = sin (α + β), so that by Ptolemy’s Theorem,

1 · sin (α + β) = sin α · cos β + cos α · sin β,

which is the addition formula for the sine function! (The difference formula sin (α − β) = sin α · cos β − cos α · sin β can likewise be obtained by considering a quadrilateral in which one side, say AD, coincides with the diameter; see fig. 38.) Thus what is perhaps the single most important formula in trigonometry was already known to Ptolemy, who used it to great effect in calculating his table of chords; and quite possibly it was discovered already by Hipparchus two and a half centuries earlier. The old adage is still true: “Nothing is new under the sun.”

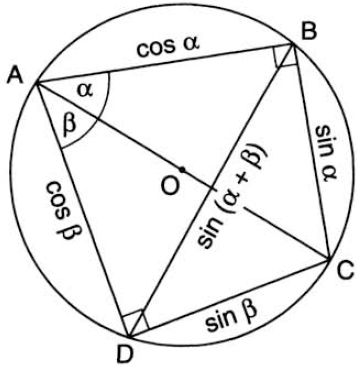
FIG. 37. Geometric proof of sin (α + β) = sin α cos β + cos α sin β.

FIG. 38. Geometric proof of sin (a − β) = sin α cos β – cos α sin β.

NOTES AND SOURCES

1. Euclid, The Elements, translated with introduction and commentary by Sir Thomas Heath (Annapolis: St. John’s College Press, 1947), vol. 2, pp. 46–49.

2. Tobias Dantzig, in his book The Bequest of the Greeks (New York: Charles Scribner’s Sons, 1955), p. 173, suggests that the theorem might have been discovered by Apollonius, who lived three centuries before Ptolemy.

3. Euclid, The Elements, vol. 2, pp. 225–228.

4. Loomis, The Pythagorean Propositon (1940; rpt. Washington, D.C.: The National Council of Teachers of Mathematics, 1968), p. 66. None of the 256 proofs relies on trigonometry: “There are no trigonometric proofs (of the Pythagorean Theorem], because all the fundamental formulae of trigonometry are themselves based upon the truth of the Pythagorean Theorem…. Trigonometry is because the Pythagorean Theorem is” (p. 244). Among the proofs there is one (number 231) proposed by James A. Garfield in 1876, five years before he became president of the United States.