Chords
The knowledge comes from the shadow, and the shadow comes from the gnomon.
—From the Chou-pei Suan-king (ca. 1105 B.C.), cited in David E. Smith, History of Mathematics, vol. 2, p. 603
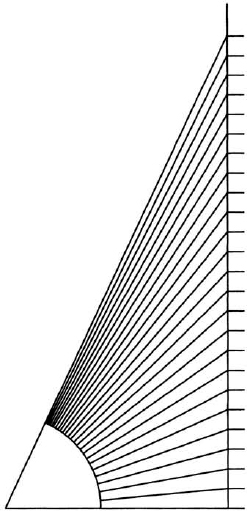
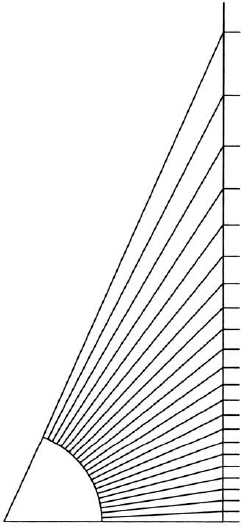
When considered separately, line segments and angles behave in a simple manner: the combined length of two line segments placed end-to-end along the same line is the sum of the individual lengths, and the combined angular measure of two rotations about the same point in the plane is the sum of the individual rotations. It is only when we try to relate the two concepts that complications arise: the equally spaced rungs of a ladder, when viewed from a fixed point, do not form equal angles at the observer’s eye (fig. 7), and conversely, equal angles, when projected onto a straight line, do not intercept equal segments (fig. 8). Elementary plane trigonometry—roughly speaking, the trigonometry known by the sixteenth century—concerns itself with the quantitative relations between angles and line segments, particularly in a triangle; indeed, the very word “trigonometry” comes from the Greek words trigonon = triangle, and metron = measure.1
As we have seen, the Egyptians used a kind of primitive trigonometry as early as the second millennium B.C. in building their pyramids. In Mesopotamia, Babylonian astronomers kept meticulous records of the rising and setting of stars, of the motion of the planets and of solar and lunar eclipses, all of which required familiarity with angular distances measured on the celestial sphere.2 The gnomon, a simple device for telling the hour from the length of the shadow cast by a vertical rod, was known to the early Greeks, who, according to the historian Herodotus (ca. 450 B.C.), got it from the Babylonians. The gnomon is essentially an analog device for computing the cotangent function: if (see fig. 9) h denotes the height of the rod and s the length of its shadow when the sun is at an altitude of α degrees above the horizon, then s = h cot α, so that s is proportional to cot α. Of course, the ancients were not interested in the cotangent function as such but rather in using the device as a timekeeper; in fact, by measuring the daily variation of the shadow’s length at noon, the gnomon could also be used to determine the day of the year.
FIG. 7. Equal vertical increments subtend unequal angles.
Thales of Miletus (ca. 640–546 B.C.), the first of the long line of Greek philosophers and mathematicians, is said to have measured the height of a pyramid by comparing the shadow it casts with that of a gnomon. As told by Plutarch in his Banquet of the Seven Wise Men, one of the guests said to Thales:
Whereas he [the king of Egypt] honors you, he particularly admires you for the invention whereby, with little effort and by the aid of no mathematical instrument, you found so accurately the height of the pyramids. For, having fixed your staff erect at the point of the shadow cast by the pyramid, two triangles were formed by the tangent rays of the sun, and from this you showed that the ratio of one shadow to the other was equal to the ratio of the [height of the] pyramid to the staff.3
FIG. 8. Equal angles subtend unequal vertical increments.
Again trigonometry was not directly involved, only the similarity of two right triangles. Still, this sort of “shadow reckoning” was fairly well known to the ancients and may be said to be the precursor of trigonometry proper. Later, such simple methods were successfully applied to measure the dimensions of the earth, and later still, the distance to the stars (see chapter 5).
Trigonometry in the modern sense of the word began with Hipparchus of Nicaea (ca.190–120 B.C.), considered the greatest astronomer of antiquity. As with many of the Greek scholars, Hipparchus’s work is known to us mainly through references by later writers, in this case the commentary on Ptolemy’s Almagest by Theon of Alexandria (ca. 390 A.D.). He was born in the town of Nicaea (now Iznik in northwest Turkey) but spent most of his life on the island of Rhodes in the Aegean Sea, where he set up an observatory. Using instruments of his own invention, he determined the positions of some 1,000 stars in terms of their celestial longitude and latitude and recorded them on a map—the first accurate star atlas (he may have been led to this project by his observation, in the year 134 B.C. of a nova—an exploding star that became visible where none had been seen before). To classify stars according to their brightness, Hipparchus introduced a scale in which the brightest stars were given magnitude 1 and the faintest magnitude 6; this scale, though revised and greatly extended in range, is still being used today. Hipparchus is also credited with discovering the precession of the equinoxes—a slow circular motion of the celestial poles once every 26,700 years; this apparent motion is now known to be caused by a wobble of the earth’s own axis (it was Newton who correctly explained this phenomenon on the basis of his theory of gravitation). And he refined and simplified the old system of epicylces, invented by Aristotle to explain the observed motion of the planets around the earth (see chapter 7); this was actually a retreat from his predecessor Aristarchus, who had already envisioned a universe in which the sun, and not the earth, was at the center.
FIG. 9. Gnomon.
To be able to do his calculations Hipparchus needed a table of trigonometric ratios, but he had nowhere to turn: no such table existed, so he had to compute one himself. He considered every triangle—planar or spherical—as being inscribed in a circle, so that each side becomes a chord. In order to compute the various parts of the triangle one needs to find the length of the chord as a function of the central angle, and this became the chief task of trigonometry for the next several centuries. As an astronomer, Hipparchus was chiefly concerned with spherical triangles, but he must have known many of the formulas of plane trigonometry, among them the identities (in modern notation) sin2 α + cos2 α = 1, sin2 α/2 = (1 – cosα)/2, and sin (α ± β) = sin α cos β. ± cos α sin β. These formulas, of course, were derived by purely geometric means and expressed as theorems about the angles and chords in a circle (the first formula, for example, is the trigonometric equivalent of the Pythagorean Theorem); we will return to some of these formulas in chapter 6. Hipparchus wrote twelve books on the computation of chords in a circle, but all are lost.
The first major work on trigonometry to have come to us intact is the Almagest by Claudius Ptolemaeus, commonly known as Ptolemy (ca. 85–ca. 165 A.D.).4 Ptolemy lived in Alexandria, the intellectual center of the Hellenistic world, but details of his life are lacking (he is unrelated to the Ptolemy dynasty that ruled Egypt after the death of Alexander the Great in 323 B.C.). In contrast to most of the Greek mathematicians, who regarded their discipline as a pure, abstract science, Ptolemy was first and foremost an applied mathematician. He wrote on astronomy, geography, music, and possibly also optics. He compiled a star catalog based on Hipparchus’s work, in which he listed and named forty-eight constellations; these names are still in use today. In his work Geography, Ptolemy systematically used the technique of map projection (a system for mapping the spherical earth onto a flat sheet of paper), which Hipparchus had already introduced; his map of the then known world, complete with a grid of longitude and latitude, was the standard world map well into the Middle Ages (fig. 10). However, Ptolemy seriously underestimated the size of the earth, rejecting Eratosthenes’ correct estimate as being too large (see chapter 5). In hindsight this turned out to be a blessing, for it spurred Columbus to attempt a westward sea voyage from Europe to Asia, an endeavor which brought about the discovery of the New World.
Ptolemy’s greatest work is the Almagest, a summary of mathematical astronomy as it was known in his time, based on the assumption of a motionless earth seated at the center of the universe and the heavenly bodies moving around it in their prescribed orbits (the geocentric system). The Almagest consists of thirteen parts (“books”) and is thus reminiscent of the thirteen books of Euclid’s Elements. The similarity goes even further, for the two works contain few of their authors’ own discoveries; rather, they are compilations of the state of knowledge of their respective fields and are thus based on the achievements of their predecessors (in Ptolemy’s case, mainly Hipparchus). Both works have exercised an enormous influence on generations of thinkers; but unlike the Elements, which to this day forms the core of classical geometry, the Almagest lost much of its authority once Copernicus’s heliocentric system was accepted. As a consequence, it is much less known today than the Elements— an unfortunate state of affairs, for the Almagest is a model of exposition that could well serve as an example even to modern writers.
FIG. 10. Ptolemy’s world map.
The word Almagest had an interesting evolution: Ptolemy’s own title, in translation, was “mathematical syntaxis,” to which later generations added the superlative megiste (“greatest”). When the Arabs translated the work into their own language, they kept the word megiste but added the conjunction al (“the”), and in due time it became known as the Almagest.5 In 1175 the Arab version was translated into Latin, and from then on it became the cornerstone of the geocentric world picture; it would dominate the scientific and philosophical thinking of Europe well into the sixteenth century and would become the canon of the Roman Church.
![]()
Of special interest to us here is Ptolemy’s table of chords, which is the subject of chapters 10 and 11 of the first book of the Almagest. His table gives the length of a chord in a circle as a function of the central angle that subtends it (fig. 11) for angles from 0° to 180° at intervals of half a degree. A moment’s thought will show that this is essentially a table of sines: denoting the radius by r, the central angle by α, and the length of the chord by d, we have
FIG. 11.
d = chord α = 2r sin α/2.
Ptolemy takes the diameter of the circle to be 120 units, so that r = 60 (the reason for this choice will soon become clear). Equation (1) then becomes d = 120 sin α/2. Thus, apart from the proportionality factor 120, we have a table of values of sin α/2 and therefore (by doubling the angle) of sin α.
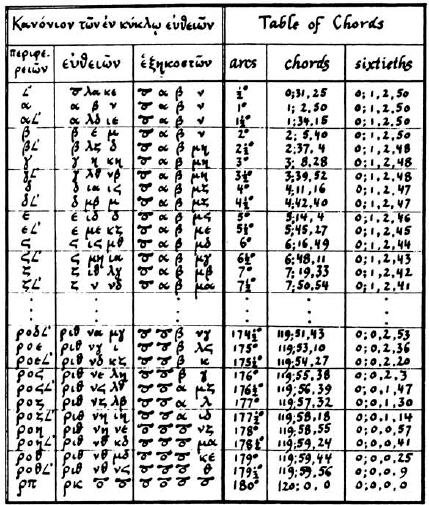
In computing his table Ptolemy used the Babylonian sexagesimal or base 60 numeration system, the only suitable system available in his day for handling fractions (the decimal system was still a thousand years in the future). But he used it in conjunction with the Greek system in which each letter of the alphabet is assigned a numerical value: α = 1, β = 2, and so on. This makes the reading of his table a bit cumbersome, but with a little practice one can easily become proficient at it (fig, 12). For example, for an angle of 7° (expressed by the Greek letter ζ), Ptolemy’s table gives a chord length of 7; 19, 33 (written as ζ ιθ λγ, the letters ι, θ, λ, and γ representing 10, 9, 30, and 3, respectively), which is the modern notation for the sexagesimal number 7 + 19/60 + 33/3,600 (the semicolon is used to separate the integral part of the number from its fractional part, and the commas separate the sexagesimal positions). When written in our decimal systems, this number is very nearly equal to 7.32583; the true length of the chord, rounded to five places, is 7.32582. Quite a remarkable achievement!
FIG. 12. A section from Ptolemy’s table of chords.
Ptolemy’s table gives the chord length to an accuracy of two sexagesimal places, or 1/3,600, which is sufficient for most applications even today. Moreover, the table has a column of “sixties” that allows one to interpolate between successive entries: it gives the mean increment in the chord length from one entry to the next, that is, the increment divided by 30 (the interval between successive angles, measured in minutes of arc).6 In computing his table, Ptolemy used the formulas mentioned earlier in connection with Hipparchus, all of which are proved in the Almagest.7
Ptolemy now shows how the table can be used to solve any planar triangle, provided at least one side is known. Following Hipparchus, he considers the triangle to be inscribed in a circle. We will show here the simplest case, that of a right triangle.8 Let the triangle be ABC (fig. 13), with the right angle at C. From elementary geometry we know that the hypotenuse c = AB is the diameter of the circle passing through A, B, and C. Denoting by O the center of this circle (that is, the midpoint of AB), a well-known theorem says that ∠BOC = 2∠BAC = 2a. Suppose that α and c are given. We first compute 2α and use the table to find the length of the corresponding chord; and since the table assumes c 120, we have to multiply the length by the ratio c/120. This gives us the side α = BC. The remaining side b = AC can then be found from the Pythagorean Theorem, and the angle β = ∠ABC from the equation α = 90° – α. Conversely, if two sides are known, say α and c, we compute the ratio a/c, multiply it by 120, and then use the table in reverse to find 2a and thence α.
FIG. 13. Right triangle inscribed in a circle.
The procedure can be summarized in the formula
where chord 2α is the length of the chord whose central angle is 2α. This leads to an interesting observation: in the sexagesimal (base 60) system, multiplying and dividing by 120 is analogous to multiplying and dividing by 20 in the decimal system: we simply multiply or divide by 2 and shift the point one place to the right or left, respectively. Thus equation (2) requires us to double the angle, look up the corresponding chord, and divide it by 2. To do this again and again becomes a chore, so it was only a matter of time before someone shortened this labor by tabulating half the chord as a function of twice the angle, in other words our modern sine function.9 This task befell the Hindus.
1. As proof that the relation between angles and line segments is far from simple, consider the following theorem: If two angle-bisectors in a triangle are equal in length, the triangle is isosceles. Looking deceptively simple, its proof can elude even experienced practitioners. See H.S.M. Coxeter, Introduction to Geometry (New York: John Wiley, 1969), pp. 9 and 420.
2. For a good summary of Babylonian astronomy, see Otto Neugebauer, The Exact Sciences in Antiquity (1957; 2d ed., New York: Dover, 1969), chapter 5.
3. As quoted in David Eugene Smith, History of Mathematics (1925; rpt. New York: Dover, 1958), vol. II, pp. 602–603.
4. Asger Aaboe, in Episodes from the Early History of Mathematics New York: Random House, 1964), gives his name as Klaudios Ptolemaios, which is closer to the Greek pronunciation. I have used the more common Latin spelling Ptolemaeus.
5. Smith (History of Mathematics, vol. I, p. 131) comments that since the prefix “al” means “the,” “to speak of ‘the Almagest’ is like speaking of ‘the the-greatest.’ Nevertheless, the misnomer is so common that I have kept it here.
6. This column is akin to the “proportional parts” column found in a table of logarithms.
7. For a full discussion of how Ptolemy compiled his table, see Aaboe, Episodes, pp. 112–126.
8. The other cases can be handled by dissecting the triangle into right triangles; see ibid., pp. 107–111.
9. This becomes clear from the right triangle ABC (fig. 13), in which α = c sin α. Comparing this with equation (2), we have sin α = (chord 2α)/120.