5

Measuring Heaven and Earth

The science of trigonometry was in a sense a precursor of the telescope. It brought faraway objects within the compass of measurement and first made it possible for man to penetrate in a quantitative manner the far reaches of space.

—Stanley L. Jaki, The Relevance of Physics (1966).

Since its earliest days, geometry has been applied to practical problems of measurement—whether to find the height of a pyramid, or the area of a field, or the size of the earth. Indeed, the very word “geometry” derives from the Greek geo (earth) and metron (to measure). But the ambition of the early Greek scientists went even farther: using simple geometry and later trigonometry, they attempted to estimate the size of the universe.

Aristarchus of Samos (ca. 310–230 B.C.) is considered the first great astronomer in history. Whereas most of his predecessors had derived their picture of the cosmos from aesthetic and mythological principles, Aristarchus based his conclusions entirely on the observational data available to him. For example, he pointed out that the motion of the planets could best be accounted for if we assume that the sun, and not the earth, is at the center of the universe—this almost two thousand years before Copernicus proposed his heliocentric system.¹ Most of Aristarchus’s writings are lost, but one work, On the Sizes and Distances of the Sun and Moon, a treatise on mathematical astronomy, has survived. In it he developed a geometric method for determining the ratio of the distances of the sun and moon from the earth.

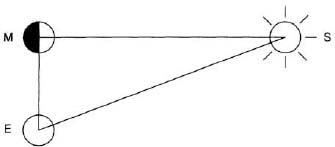
His method, known as “lunar dichotomy” (from the Greek dichotomos, to divide into two parts), was based on the fact that at the moment when exactly half of the moon’s disk appears to be illuminated by the sun, as happens twice during each lunar cycle, the lines of sight from the earth to the moon and from the moon to the sun form a right angle (fig. 22). It follows that if we know angle MES, we can, in principle, find the ratios of the sides of triangle EMS, and in particular the ratio ES/EM. Aristarchus says that ∠MES is “less than a quadrant by a thirtieth of a quadrant,” that is, ∠MES = 90° – 3° = 87°. Using modern trigonometry, it then follows that ES/EM = sec 87° = 19.1. Aristarchus, of course, did not have trigonometric tables at his disposal, so he had to rely on a theorem that, in modern notation, says: if α and β are two acute angles and α > β, then (sin α)/(sin β) < α/β < (tan α)/(tan β).² From this he concluded that ES/EM is greater than 18:1 but less than 20:1.

Now this estimate of the ratio ES/EM falls far short of the actual value, about 390. The reason is that Aristarchus’s method, while sound in principle, was woefully impractical to implement. For one, it is extremely difficult to determine the exact moment of dichotomy, even with a modern telescope; and second, it is just as difficult to measure the angle MES —one must look directly into the sun, and the sun may have already set at the instant of dichotomy. Furthermore, because ∠MES is very close to 90°, a small error in its determination leads to a large error in the ratio ES/EM. For example, if ∠MES were 88° instead of 87°, ES/EM would be 28.7, while for 86° it would be 14.3. Still, Aristarchus’s method marks the first attempt to estimate the dimensions of our planetary system based on an actual measurement of observable quantities.

Aristarchus also estimated the ratio of the sizes of the sun and moon. During a total eclipse of the sun, the moon completely covers the solar disk—but just barely so, which is why the duration of totality is so short—no longer than about seven minutes, and usually much less.³ This means that the apparent sizes of the sun and moon as seen from the earth are roughly equal (about half a degree of arc as measured on the celestial sphere). Therefore the ratio of the actual diameters of these bodies must be nearly the same as the ratio of their distances from the earth. Aristarchus thus concluded that the sun’s diameter is between 18 and 19 times that of the moon. The actual ratio is about 400.

FIG. 22. Aristarchu’s method.

Now it is one thing to estimate the ratio of distances of two faraway objects, but quite another to estimate their actual distances and sizes. Here the phenomenon of parallax plays a crucial role. It is a common experience that an object appears to change its position—as viewed against a remote background—when the observer changes his own position, or when viewed simultaneously by two observers at different places. If one knows the distance between the two observers (the length of the baseline) then, by measuring the apparent angular shift in the position of the object (the angle of parallax), one can find the distance to the object, using simple trigonometry. The method of parallax is the basis of terrestrial surveying, but when applied to the vast distances between celestial bodies, its accuracy is limited: the farther the object, the smaller its angle of parallax and the greater the uncertainty in estimating its distance.

Because the moon is relatively close to us, its apparent shift in position as seen by two observers at different locations on the earth, though small by terrestrial standards, is considerable on an astronomical scale. Still, to be of any practical use, the two observers must be stationed as far from each other as possible—ideally at opposite points on the earth. However, during the rare occurrence of a total solar eclipse, even a slight change in the observer’s position can mean the difference between total darkness and a partially eclipsed sun. This was dramatically shown during the eclipse of January 24, 1925, which passed right through New York City and was watched by millions of people in clear skies. To determine the exact edge of the moon’s shadow, observers were stationed at every intersection between 72nd and 135th Streets in Manhattan and instructed to report whether they had seen the sun’s corona—visible only during totality, when the solar disk is completely covered by the moon—or merely a narrow crescent sun, indicating that the eclipse was partial. “The results were definite: the edge of the umbra [the moon’s shadow] passed between 95th and 97th Streets, yielding an accuracy of several hundred feet for a shadow cast at a distance of over 200,000 miles.”⁴

The first to use lunar parallax to estimate the moon’s distance was Hipparchus of Nicaea, whom we have already met in chapter 2. Hipparchus carefully studied ancient Babylonian eclipse records dating back to the eighth century B.C., and from these he gained a thorough understanding of the motion of the sun and moon. By a fortunate coincidence, a solar eclipse had occurred not far from his birthplace just a few years before he was born; this eclipse, recently identified as that of March 14, 189 B.C., was total near the Hellespont (the straight of Dardanelles in modern Turkey), whereas in Alexandria only four-fifths of the sun’s disk were hidden by the moon. Since the sun and moon subtend about half a degree of arc as measured on the celestial sphere, the moon’s apparent shift in position amounted to one-fifth of this, or about 6 arc minutes. Combining this information with the longitude and latitude of the two places and the elevation of the sun and moon at the time of the eclipse, Hipparchus was able to calculate the moon’s least and greatest distance as 71 and 83 earth radii, respectively. While these estimates are in excess of the modern values of 56 and 64, they came within the correct order of magnitude and should be considered a remarkable achievement for his time.⁵

Hipparchus had estimated the moon’s distance in terms of earth radii. To express this distance in more common units, one must know the size of the earth. The notion that the earth is spherical is attributed to Pythagoras; whether he derived this idea from observational evidence (for example, from the fact that during a partial lunar eclipse the earth always casts a circular shadow on the moon) or, as is more likely, from aesthetic and philosophical principles (the sphere being the most perfect of all shapes) is not known. But once the notion of a spherical earth took hold, attempts were made to determine its size. The credit for achieving this feat goes to a brilliant mathematician and geographer of the second century B.C., Eratosthenes of Cyrene (ca. 275–194 B.C.).

Eratosthenes was a friend of Archimedes, the greatest scientist of the ancient era, who addressed to him several of his works. As with most scholars in earlier times, Eratosthenes was active in several disciplines. He prepared a celestial map that included 675 stars, and he determined the angle of inclination of the equator to the ecliptic (the plane of earth’s orbit around the sun)—about 23.5°. He suggested to add to the calendar one extra day every four years to keep it in step with the seasons, an idea on which the Julian calendar was later based. In mathematics he devised the famous “sieve” for finding the prime numbers, and he gave a mechanical solution to the duplication problem: to find the side of a cube whose volume equals twice that of a given cube. Eratosthenes also wrote poetry and literary critique, and was the first to undertake a scientific chronology of major historical events going back to the Trojan War. His friends nicknamed him “Beta,” perhaps because they ranked him second to Archimedes; but this slight did not prevent Ptolemy III, the ruler of Egypt, to call upon him to head the great library of Alexandria, the largest repository of scholarly works in the ancient world. In old age he became blind, and sensing that his productive years were over, died a “philosopher’s death” by voluntary starvation.

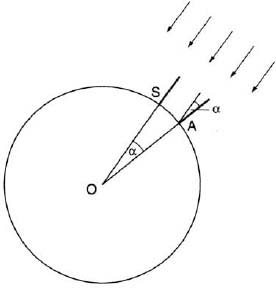
In the year 240 B.C. Eratosthenes achieved the feat for which he is chiefly remembered: computing the size of the earth. It was known that at noon on the day of the summer solstice (the longest day of the year), the sun’s rays directly illuminated the bottom of a deep well in the town of Syene (now Aswan) in Upper Egypt; that is, on that day the sun was exactly overhead at noon. But in Alexandria, due north of Syene, the sun at that moment was one-fiftieth of a full circle (i.e., 7.2°) from the zenith, as measured by the shadow of a vertical rod (fig. 23). Eratosthenes assumed that the sun is so far away from the earth that its rays reach us practically parallel; hence the diffference in the sun’s elevation as seen from the two locations must be due to the sphericity of the earth. Since the distance between Alexandria and Syene was 5,000 stadia (as measured by the time it took the king’s messengers to run between the two cities), the circumference of the earth must be fifty times this distance, or 250,000 stadia.

Unfortunately, the exact length of the stadium, the geographical distance unit in the Greek era, is not known; estimates vary from 607 to 738 feet, the smaller figure referring to the Roman stadium of later use. The circumference of the earth as found by Eratosthenes is therefore between 29,000 and 35,000 miles, whereas the correct values are 24,818 miles for the polar circumference and 24,902 miles for the equatorial.⁶ Eratosthenes thus came remarkably close, and in doing so he used the science of geometry in its literal sense: to measure the earth.

FIG. 23. Eratosthenes’s measurement of the earth’s circumference.

Ferdinand Magellan’s historic circumnavigation of the globe (1519–1522) provided the first direct proof that the earth is roughly spherical. But soon thereafter scientists began to suspect that it might actually be flattened; the question was, was it flattened at the poles (an oblate spheroid) or at the equator (a prolate spheroid)? This was not merely an academic issue: with the age of exploration well under way, it became crucial for navigators to be able to determine their position at sea—their longitude and latitude—with sufficient accuracy. This in turn depended on knowing the length of a degree of latitude as measured along a meridian (a “meridional degree”). Had the earth been a perfect sphere, a degree would have the same length everywhere, regardless of the latitude itself. But if the earth was oblate, the length of a degree would increase slightly toward the poles, while if it was prolate, the length would decrease. Determining the exact shape of the earth—and more generally, of any curved surface—evolved into the science of geodesy. Some of the greatest mathematicians of the eighteenth and nineteenth centuries tackled this problem, among them Newton, Euler and Gauss.

The first step in a geodetic survey is to select a baseline of known length, and then measure the angles between this line and the lines of sight from its endpoints to a distant landmark. For relatively small regions—a town or a county—one may ignore the earth’s curvature and regard the region as planar; one can then compute the distance from either endpoint to the landmark, using the Law of Sines (the ASA case). These distances can now be used as new baselines and the process repeated, until the entire region is covered by a network of triangles. This process is known as triangulation; it provides the skeleton on which the topographical details of the land—hills, rivers, lakes, towns, and roads—are later superimposed to form a complete map.⁷

The method of triangulation was suggested as early as 1533 by the Dutch mathematician Gemma Frisius (1508–1555).⁸ It was first carried out on a large scale by another Dutchman, Willebrord van Roijen Snell (1581–1626),⁹ who in 1615 surveyed a stretch of 80 miles in Holland, using a grid of 33 triangles. But it was in France that the first comprehensive, government-sponsored triangulation effort was undertaken in 1668 under the direction of the Abbé Jean Picard (1620–1682), one of the founders of the Paris Observatory. As his baseline he chose a 7 mile stretch along the road from Paris to Fontainbleau; from this baseline the survey would eventually cover all of France. To improve the accuracy of his measurements, Picard used a new type of quadrant (an instrument for measuring vertical angles) in which a telescope with cross hairs replaced the two pinholes for sighting. Combining his terrestrial measurements with an astronomical determination of the latitudes of the endpoints of his baseline, Picard arrived at the value of 68.65 miles for the degree at the latitude of Paris. He then extended his survey to the French coastline, which resulted in an unwelcome discovery: the west coast of the country had to be shifted 1° eastward relative to the prime meridian through Paris, causing the monarch Louis XIV to exclaim: “Your journey has cost me a major portion of my realm!”¹⁰

After Picard’s death in 1682 the survey was continued for another century by four generations of a remarkable family of astronomers, the Cassini family. Giovanni Dominico Cassini (1625–1712) was born in Italy and taught at the University of Bologna, but in 1668, as a result of Picard’s persistent efforts, he left his post and became head of the newly founded Paris Observatory. Changing his name to Jean Dominique, he made significant contributions to astronomy: a determination of the rotation periods of Mars and Jupiter, the first study of the zodiacal light (a faint glow that stretches up the eastern sky before sunrise and the western sky after sunset), the discovery of four of Saturn’s satellites and a dark gap in Saturn’s rings (known as the Cassini Division), and a measurement of the parallax of Mars in 1672 from which he was able to calculate—using Kepler’s laws of planetary motion—the distance from the earth to the sun as 87 million miles, the first determination to come close to the actual value of about 93.5 million miles. Amazingly, he was also one of the last professional astronomers to oppose Copernicus’s heliocentric system, and he remained convinced that the earth was a prolate spheroid, despite mounting evidence to the contrary.¹¹

In later life Cassini increasingly devoted himself to geodesy and cartography, using his astronomical expertise to the fullest. In 1679 he conceived a new world map, the planisphère terrestre, using a projection on which all directions and distances from the north pole are shown correctly; this is known as the azimuthal equidistance projection (see chapter 10). Cassini’s huge map, 24 feet in diameter, was drawn on the third floor of the Paris Observatory; it became a model for future cartographers and was reproduced and published in 1696.

But Cassini did not rest on his laurels. Now seventy, he resumed the survey of France with renewed vigor, assisted by his son Jacques (1677–1756). Their goal: to extend the survey south to the Pyrenees and eventually cover all of Europe with a network of triangles. As a by-product, they hoped to find out whether the earth was prolate or oblate.

The elder Cassini died in 1712 at the age of eighty-seven. His son now realized that the issue could only be resolved by comparing the length of a degree at widely separated latitudes, and he suggested that expeditions be sent to the equator and the arctic region to settle the question once and for all. At stake was not only a theoretical interest in the shape of the earth; the prestige of France itself was in the balance. Newton had predicted that the earth is flattened at the poles, basing his argument on the interaction between the gravitational pull of the earth on itself and the centrifugal forces due to its spinning on its axis. In France, however, Newton’s ideas on gravitation—especially his notion of “action at a distance”—were rejected in favor of Descartes’ theory of vortices, which held that gravitational attraction is caused by huge vortices swirling around in a fluid that permeates all space. “The figure of the earth had become a cause célèbre, the most debated scientific issue of the day, with French and British national pride at stake.”¹²

The evidence, though indirect, tended to support Newton. For one, the planet Jupiter as seen through even a small telescope shows considerable flattening at the poles; and here on earth, measurements of the acceleration due to gravity, as obtained from the period of a swinging pendulum, showed a slightly smaller value at the equator than at the poles, indicating that the equator is farther away from the center of the earth than the poles.

Following Jacques Cassini’s suggestion and with the blessing of the new monarch, Louis XV, the Académie Royale de Sciences—the French equivalent of the Royal Society in England—in 1734 authorized two expeditions, one to be sent to Lapland on the Swedish-Finnish border, the other to Peru, close to the equator. Their mission: carry out a full-scale triangulation of their respective regions and determine the length of the degree at each location.

The first expedition was headed by Pierre Louis Moreau de Maupertuis (1698–1759), who began his career in the French army and later became a mathematician and physicist (he was the first to formulate the principle of least action and later used it to “prove” the existence of God). As a lone supporter and admirer of Newton on the Continent, he was only too eager to join an endeavor that, he hoped, would prove his master right. Going with him was another French mathematician, Alexis Claude Clairaut (1713–1765), who as a young prodigy had studied calculus when he was ten and published his first book at eighteen (the differential equation xy′ – y = f (y′), where f is a given function of the derivative y′, is named after him). The Peru expedition was headed by a geographer, Charles Marie de La Condamine (1701–1774), and it too included a mathematician, Pierre Bouger (1698–1758). The participation of so many first-rank mathematicians in field trips to remote countries was in line with a long French tradition of producing eminent scientists who also served their country in the military and civil service. We will meet some more of them in chapter 15.

The two expeditions encountered numerous hardships. The Lapland team braved blinding snowstorms and had to force its way across frozen marshes that turned into mud when spring arrived; during summer their biggest enemy was the biting mosquitoes. The Peru team fared even worse: not only did they combat altitude sickness in the high Andes, but disease and a series of accidents resulted in the death of several members. To top it all, bitter dissent broke out among the expedition leaders, who returned home separately. Nevertheless the two expeditions accomplished their tasks: they found the length of a degree to be 69.04 miles in Lapland and 68.32 miles in Peru (fig. 24). Combined with Picard’s value of 68.65 miles at Paris, their results proved beyond doubt that the earth is an oblate spheroid. Newton was proven right—again.

And now the Cassinis returned to the scene. While the two expeditions were doing their work abroad, Jacques Cassini and his son César François (1714–1784) completed the triangulation of France, using a network of eighteen baselines and four hundred triangles. It now remained to transform the grid into an actual map, and this task was completed by Jean Dominique Cassini IV (1748–1845), great-grandson of the dynasty’s founder. His huge map, 12 by 12 yards, was published in 182 sheets on a scale of 1:86,400 and showed not only topographical features but also the location of castles, windmills, vineyards, and—this being the time of the French Revolution—guillotines. The fourth Cassini received much praise for his work—and then was arrested and tried by a revolutionary tribunal, barely saving his life. His reputation was eventually restored by Napoleon Bonaparte, and he died in 1845 at the age of ninety-seven.

FIG. 24. Measuring a degree of longitude. The map shows part of the triangulation network set up by Maupertuis’s expedition to Lapland. From a 1798 engraving (the author’s collection).

France’s geodetic lead was now followed by the rest of Europe, and by the mid-nineteenth century most of the continent was thoroughly triangulated and mapped. The task then moved overseas to India, the crown jewel of the British Empire, were a huge triangulation project, known as the Great Trigonometrical Survey, was undertaken from 1800 to 1913. Sponsored by the East India Company, the vast commercial eneterprise that virtually ruled the country from its offices in London, the survey began near Madras on the southwest coast of the Bay of Bengal and eventually reached the Himalayas in the far north.

Captain William Lambton (1753–1823), who headed the survey from 1802 until his death, was determined to achieve his goal with unprecedented accuracy. His huge theodolite, weighing half a ton, was built in London according to his specific instructions and shipped to India, being intercepted en route by a French frigate. On one occasion this monstrous instrument was hoisted to the top of the Great Temple of Tanjore (Thanjavur) so as to give the surveyors a clear view of the terrain. On the way up a rope snapped and the instrument fell to the ground and broke. Undaunted, Lambton secluded himself in his tent and for the next six weeks repaired the instrument himself.

In 1806 Lambton set out to achieve a goal even greater than the survey of India: to determine the figure of the earth. To this end he ran a line along the 78° meridian from near Cape Comorin at the southern tip of the subcontinent to the Kashmir region in the north, a distance of some 1,800 miles. His men encountered numerous perils: the intense heat of central India, thick vegetation in which tigers were roaming, the ever present threat of malaria, and angry locals who were convinced the surveyors were spying on their wives.

After Lambton’s death, the survey continued under his assistant George (later Sir George) Everest (1790–1866), who would become Surveyor General of India. Everest maintained and even exceeded the high standards of his predecessor. To make up for the absence of natural landmarks in the vast plains of central India, he built a series of towers visible from far away, many of which still stand today. And to avoid the heat and haze in the country’s interior, he ordered his surveyors to work at night, relying on bonfires lit from the top of his towers as signals. During daytime he used a heliograph—a specially designed mirror whose reflected sunlight could be seen from 50 miles away. Everest’s meticulous care for detail paid off: when the survey reached the foothills of the Himalayas, his actual position differed from that computed from his triangulation by 7 inches over a distance of 500 miles!

FIG. 25. Surveying instruments of the nineteenth century.

During his survey Everest made a discovery that is still being debated today: he found that the great mass of the Himlayan mountains deflected the direction of the plumb line. These gravity anomalies were the first indication of what is now called “mascons” (mass concentrations, the term having first been applied to the moon), whose exact nature and distribution is being mapped today by satellites.

After Everest’s retirement in 1843 the survey continued under the direction of his assistant, Captain Andrew Waugh. And now the power of trigonometry to measure faraway objects reached its high point—literally. Legend has it that one day in 1852 the survey’s chief computer, Radhanath Sikdar, himself a mathematician, burst into Waugh’s office exclaiming, “Sir, I have discovered the highest mountain in the world.” The official announcement was delayed until 1856 so as to check and recheck the height of Peak XV, as Mount Everest was temporarily named (it is also known by its Tibetan name Chomolungma, “goddess mother of the world”). Averaging several readings taken at a distance of some 100 miles, the mountain’s height turned out exactly 29,000 feet; but fearing that such a round figure might appear as if it had been made up, the surveyor arbitrarily added two feet, and until 1954 the official height of the world’s highest peak remained 29,002 feet above sea level. It is now put at 29,035 feet.¹³

While the French were busy triangulating Europe and the British surveyed their empire, Friedrich Wilhelm Bessel (1784–1846) in Germany was set on triangulating the heavens. Beginning his career as an accountant, he taught himself mathematics and astronomy and at the age of twenty recalculated the orbit of Halley’s comet, taking into account the gravitational perturbations exerted on it by the planets Jupiter and Saturn. Bessel’s achievements brought him to the attention of the leading German astronomer at the time, Heinrich Olbers, who secured him a position at the observatory of Lilienthal. His reputation as a skilled observational astronomer as well as a theoretician of the first rank led to his appointment in 1809 as director of the Prussian Royal Observatory at Königsberg (now Kaliningrad in Russia), a position he kept until his death.¹⁴

By 1800 the size of the then-known solar system was fairly well established (though the planets Neptune and Pluto had yet to be discovered), but the dimensions of the universe beyond was a different matter: no one had the faintest idea how far were the fixed stars. The method of parallax, so successful in determining the distances of solar system objects, had thus far failed when applied to the fixed stars: no star showed any measurable shift in position even when using the largest baseline available to us—the diameter of earth’s orbit around the sun. In fact, the absence of parallax was taken by the Greeks as the strongest evidence for their picture of a universe in which a motionless earth was permanently fixed at the center. Copernicus interpreted the facts differently: to him the absence of any discernible parallax indicated that the stars are so far away from us that any apparent shift in their position due to earth’s motion around the sun would be far too small to be detected by our eyes.

When the telescope was invented in 1609 it became theoretically possible to look for the parallax of some nearby stars, but all such attempts have failed. One reason was that astronomers were looking only at the brightest stars in the sky, assuming that their brightness indicated that they were also the nearest. This would be true if all stars had the same intrinsic brightness—the same light output—like street lights lining up an avenue. But by 1800 astronomers knew that stars differ vastly in their intrinsic brightness, and consequently their apparent brightness could not be used as an effective yardstick in estimating their relative distance. Instead, the search turned to stars with a large proper motion—the actual motion of a star relative to the distant sky (as opposed to apparent motion, which is merely due to the observer’s own motion). It was correctly assumed that a large proper motion would be an indication that the star is relatively close by.

Soon a candidate was found—the star 61 Cygni in the constellation Cygnus, the Swan. This fifth-magnitude star is barely visible to the naked eye but was known to have a considerable proper motion—5.2 arc seconds per year, or about one moon diameter every 350 years. Bessel now directed all his efforts at this star. After 18 months of intense observation, he announced in 1838 that 61 Cygni showed a parallax of 0.314 arc seconds (by comparsion, the moon’s apparent diameter is about half a degree of arc, or 1,800 arc seconds). This minute figure was enough for Bessel to find the star’s distance, using the simplest of trigonometric calculations. Because this event marks a milestone in the history of astronomy, we give the details here.

In figure 26 let S represent the sun, E₁ and E₂ the earth at opposite positions in its orbit around the sun, and T the star in question. By astronomical convention, the annual parallax is defined as half the angular shift in the star’s position due to earth’s motion around the sun, that is, the angle α = ∠E₁TS in the right triangle E₁ST. Denoting the distance to the star by d and the radius of earth’s orbit by r, we have sin α = r/d, or

Substituting the values r = 150,000,000 km = 1.5 × 10⁸ km and α = 0.314″ = (0.314/3, 600)°, we get d = 9.85 × 10¹³ km. Now, stellar distances are usually expressed in light years, so we must divide this figure by the speed of light, 3 x 10⁵ km/sec, times the number of seconds in a year, 3,600 × 24 × 365. This gives us

d = 10.1 light years.

Thus the dimensions of the universe beyond our solar system became known. The parallax of 61 Cygni has since been refined to 0.294″, resulting in a distance of 11.1 light years. Soon other stellar parallaxes were successfully measured, among them that of Alpha Centauri, which at 4.3 light years is our closest celestial neighbor beyond the sun.¹⁵ The method has been applied to stars up to about a hundred light years away, but for greater distances its accuracy quickly diminishes. Fortunately other methods, based on a star’s physical characteristics, have been developed in the strive to establish a reliable stellar distance scale.

FIG. 26. Stellar parallax.

In 1844 Bessel made a second epochal discovery: he directed his telescope to Sirius, the brightest star in the sky, and found that its proper motion shows a minute wavelike pattern; this he correctly attributed to the gravitational influence of an invisible companion that revolves around Sirius. This companion, Sirius B, was discovered in 1862 by the American telescope maker Alvan Graham Clark (1832–1897).

Gravitational perturbations have occupied Bessel’s mind through much of his life. This subject presented one of the most difficult problems in celestial mechanics, and to deal with it he introduced a certain class of functions known since as the Bessel functions. These are solutions of the differential equation x ²y ″ + xy ′ + (x ² – n ²)y = 0, where n ≥ 0 is a constant (not necessarily an integer). The nature of the solutions greatly depends on n : for n = 1/2, 3/2, 5/2,…, they can be written in closed form in terms of the functions x, sin x and cos x; otherwise they can only be expressed as infinite series and are therefore considered “nonelementary” or “higher” functions. The Bessel equation shows up in many applications; for example, the vibrations of a circular membrane—such as a drum head—are governed by Bessel’s equation with n = 0.¹⁶

Toward the end of his life Bessel turned again to the problem of gravitational perturbations. One of the outstanding astronomical riddles at the time was the anomalies in the motion of the planet Uranus: all attempts to explain these anomalies as being caused by known planets—in particular, Jupiter and Saturn—had failed. Bessel correctly attributed them to the existence of an unknown transuranian planet, but he died a few months before this planet, Neptune, was discovered.

Bessel was one of the last great scientists who was equally at home in theory as in experiment (in this case, observational techniques). Mathematicians will remember him for the Bessel functions, but his crowning achievement was in giving us the first concrete evidence of how vast interstellar space really is. With him, the attention of astronomers began to shift from the solar system to the universe beyond.

NOTES AND SOURCES

1. See Sir Thomas. L. Heath, Aristarchus of Samos: the Ancient Copernicus (1913; rpt. New York: Dover, 1981), and Greek Astronomy (1932; rpt. New York: Dover, 1991).

2. This follows from the fact that for 0° < x < 90°, the graph of (sin x)/x is decreasing, while that of (tan x)/x is increasing; that is, (sin α)/α < (sin β)β and (tan α)α > (tan β)β.

3. In 1995 I joined a group of astronomers on an expedition to India to watch the total solar eclipse of October 24. From our sight close to the center line of the moon’s shadow, totality lasted a mere 41 seconds.

4. Quoted from Bryan Brewer, Eclipse (Seattle: Earth View, 1978), p. 31.

5. See Albert van Helden, Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley (Chicago: University of Chicago Press, 1985), p. 11. See also Toomer’s article on Hipparchus in the DSB.

6. Much scholarly debate has been devoted to the length of the stadium. Some sources give it as equal to one-tenth of a mile, or 528 feet, which would lead to a circumference of 25,000 miles. It seems, though, that this length of the stadium has been “fixed” in retrospect so as to make the circumference come close to the modern value. To quote B. L. van der Waerden in Science Awakening (New York: John Wiley, 1963), p. 230: “Since we do not know the exact length of a stadium, we can say little more than that the order of magnitude [of the earth’s circumference] is about right.” See also David Eugene Smith, History of Mathematics (1925; rpt. New York: Dover, 1958), vol. 2, p. 641.

7. The material for the narrative that follows is based on the following sources: Lloyd A. Brown, The Story of Maps (1949; rpt. New York: Dover, 1979); John Noble Wilford, The Mapmakers (New York: Alfred A. Knopf, 1981); and Simon Berthon and Andrew Robinson, The Shape of the World (Chicago: Rand McNally, 1991).

8. His real name was Gemma Régnier, but he became known as Gemma Frisius after his place of birth, Friesland. In 1541 he became professor of medicine at the University of Louvaine. His book on arithmetic (Antwerp, 1540) was highly popular and went through no fewer than sixty editions. He also wrote on geography and astronomy and suggested the method of determining longitude from the difference in local time between two places. His son Cornelius Gemma Frisius (1535–1577) continued his father’s work and served as professor of medicine at the same university.

9. He was professor of mathematics at Leyden, where he succeeded his father. He worked on astronomy, physics, and spherical trigonometry and is best known for his law of refraction in optics.

10. It was not until 1913 that France recognized the meridian through Greenwich as the prime (zero) meridian, in exchange for England “recognizing” the metric system.

11. The Cassini spacecraft launched by NASA in October 1997 on a seven-year voyage to Saturn is named after him.

12. Quoted from Berthon and Robinson, Shape of the World, p. 101.

13. Surprisingly, in his autobiography, Nothing Venture, Nothing Win (New York: Coward, McCann & Geoghegan, 1975), Sir Edmund Hillary, who with Sherpa Tenzing Norgay was the first to climb Mount Everest in 1953, still gives the mountain’s height as 29,002 feet—more than twenty years after it had officially been changed to 29,028 feet. In 1999, a survey by the Boston Museum of Science and the National Geographic Society, using the Global Positioning Satellite System, put the figure at 29,035 feet.

14. See Walter Fricke’s article on Bessel in the DSB.

15. Actually, Alpha Centauri is a triple star system, whose faintest companion, Proxima Centauri (discovered in 1915), is at present 4.2 light years away. 61 Cygni is now ranked nineteenth in the order of distance from the sun. See the article, “Our Nearest Celestial Neighbors,” by Joshua Roth and Roger W. Sinnott, Sky & Telescope, October 1996, pp. 32–34.

16. For n = 0 and 1 the Bessel functions—denoted by J ₀ (x) and J₁(x)—exhibit certain similarities to cos x and sin x, respectively; for example, J₀(0) = 1 and J₁(0) = 0, and both functions have an oscillating graph. However, their amplitudes diminish as x increases, and their zeros are not equally spaced along the x-axis, which is why the sound of a drum is different from that of a violin (see chapter 15). For details, see any book on ordinary differential equations.