Whereas the Egyptians wrote their records on papyrus and wood and the Chinese on bark and bamboo—all perishable materials—the Babylonians used clay tablets, a virtually indestructible medium. As a result, we are in possession of a far greater number of Babylonian texts than those of any other ancient civilization, and our knowledge of their history—their military campaigns, commercial transactions, and scientific achievements—is that much richer.

Among the estimated 500,000 tablets that have reached museums around the world, some 300 deal with mathematical issues. These are of two kinds: “table texts” and “problem texts,” the latter dealing with a variety of algebraic and geometric problems. The “table texts” include multiplication tables and tables of reciprocals, compound interest, and various number sequences; they prove that the Babylonians possessed a remarkably high degree of computational skills.

One of the most intriguing tablets to reach us is known as Plimpton 322, so named because it is number 322 in the G. A. Plimpton Collection at Columbia University in New York (fig. 14). It dates from the Old Babylonian period of the Hammurabi dynasty, roughly 1800–1600 B.C. A careful analysis of the text reveals that it deals with Pythagorean triples—integers a, b, c such that c² = a² + b²; examples of such triples are (3, 4, 5), (5, 12, 13) and (16, 63, 65). Because of the Pythagorean Theorem—or more precisely, its converse—such triples can be used to form right triangles with integer sides.

Unfortunately, the left end of the tablet is damaged and partially missing, but traces of modern glue found at the edge prove that the missing part broke off after the tablet was discovered, and one day it may yet show up in the antiquarian market. Thanks to meticulous scholarly research, the missing part has been partly reconstructed, and we can now read the table with relative ease. We should remember, however, that the Babylonians used the sexagesimal (base 60) numeration system, and that they did not have a symbol for zero; consequently, numbers may be interpreted in different ways, and the correct place value of the individual “digits” must be deduced from the context.

FIG. 14. Plimpton 322.

The text is written in cuneiform (wedged-shaped) characters, which were carved into a wet clay tablet by means of a stylus. The tablet was then baked in an oven or dried in the sun until it hardened to form a permanent record. Table 1 reproduces the text in modern notation, in which sexagesimal “digits” (themselves expressed in ordinary decimal notation) are separated by commas. There are four columns, of which the rightmost, headed by the words “its name” in the original text, merely gives the sequential number of the lines from 1 to 15. The second and third columns (counting from right to left) are headed “solving number of the diagonal” and “solving number of the width,” respectively; that is, they give the length of the diagonal and the short side of a rectangle, or equivalently, the length of the hypotenuse and one side in a right triangle. We will label these columns with the letters c and b, respectively. As an example, the first line shows the entries b = 1,59 and c = 2,49, which represent the numbers 1 × 60 + 59 = 119 and 2 × 60 + 49 = 169. A quick calculation then gives the other side of the triangle as a = √(169² − 119²) = 120; hence the triple (119, 120, 169) is a Pythagorean triple. Again, in the third line we read b = 1, 16, 41 = 1 × 60² + 16 × 60 + 41 = 4601 and c = 1, 50, 49 = 1 × 60² + 50 × 60 + 49 = 6649; therefore a = √(6649² − 4601²) = 4800, giving the triple (4601, 4800, 6649).

TABLE 1.

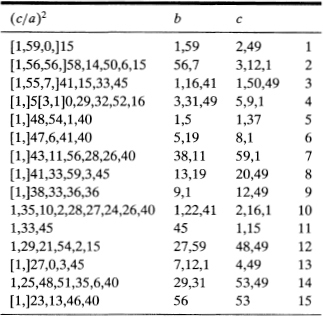
Note: The numbers in brackets are reconstructed.

The table contains some obvious errors. In line 9 we find b = 9, 1 = 9 × 60 + 1 = 541 and c = 12, 49 = 12 × 60 + 49 = 769, and these do not form a Pythagorean triple (the third number a not being an integer). But if we replace the 9, 1 by 8, 1 = 481, we do indeed get the triple (481, 600, 769). It seems that this error was simply a “typo”: the scribe must have been momentarily distracted and carved nine marks into his soft clay instead of eight; and once dried in the sun, his oversight became part of recorded history. Again, in line 13 we have b = 7, 12, 1 = 7 × 60² + 12 × 60 + 1 = 25921 and c = 4,49 = 4 × 60 + 49 = 289, and these do not form a Pythagorean triple; but we may notice that 25921 is the square of 161, and the numbers 161 and 289 do form the triple (161, 240, 289). It seems that the scribe simply forgot to take the square root of 25921. And in row 15 we find c = 53, whereas the correct entry should be twice that number, or 106 = 1, 46, producing the triple (56, 90, 106).¹ These errors leave one with a sense that human nature has not changed over the past 4000 years: our anonymous scribe was no more guilty of negligence than a student begging his or her professor to ignore “just a little stupid mistake” on the exam.²

The leftmost column is the most intriguing of all. Its heading again mentions the word “diagonal,” but the exact meaning of the remaining text is not entirely clear. However, upon examining its entries a startling fact comes to light: this column gives the square of the ratio (c/a), that is, the values of csc²α, where α is the angle opposite of side a. Let us verify this for line 1. We have b = 1,59 = 119 and c = 2,49 = 169, from which we find a = 120. Hence (c/a)² = (169/120)² = 1.983, rounded to three decimal places. The corresponding entry in column 4 is 1,59,0,15 = 1 + 59 × (1/60) + 0 × (1/60²) + 15 × (1/60³) = 1.983. (We should note again that the Babylonians did not use a symbol for the “empty slot”—our zero—and therefore a number could be interpreted in many different ways; the correct interpretation must be deduced from the context. In the example just given, we assume that the leading 1 stands for units rather than sixties.) The reader may check other entries in this column and confirm that they are equal to (c/a)².

Several questions arise: Is the order of entries in the table random, or does it follow some hidden pattern? How did the Babylonians find those particular numbers that form Pythagorean triples? And why were they interested in these numbers—specifically, in the ratio (c/a)²—in the first place? The first question is relatively easy to answer: if one compares the values of (c/a)² line by line, one discovers that they decrease steadily from 1.983 to 1.387, so it seems likely that the order of entries was determined by this sequence. Moreover, if we compute the square root of each entry in column 4—that is, the ratio c/a = csc α—and then find the corresponding angle a, we discover that α increases steadily from just above 45° to 58°. It thus seems that the author of our text was not only interested in finding Pythagorean triples, but also in determining the ratio c/a of the corresponding right triangles. This hypothesis may one day be confirmed if the missing part of the tablet will show up, as it may well contain the missing columns for a and c/a.

As to how the Pythagorean triples were found, there is only one plausible explanation: the Babylonians must have known the algorithm for generating these triples. Let u and v be any two positive integers such that u > v; then the three numbers

form a Pythagorean triple. (If in addition we require that u and v are of odd parity—one even and the other odd—and that they do not have any common factor, then (a, b, c) is a primitive Pythagorean triple, i.e., a, b, and c have no common factor.) It is easy to confirm that the numbers a, b and c as given by equations (1) satisfy the equation c² = a² + b²; the converse of this statement—that every Pythagorean triple can be found in this way—is proved in a standard course in number theory. Plimpton 322 thus shows that the Babylonians were not only familiar with the Pythagorean Theorem a thousand years before Pythagoras, but that they knew the rudiments of number theory and had the computational skills to put the theory into practice.³

NOTES AND SOURCES

(The material in this section is based on Otto Neugebauer, The Exact Sciences in Antiquity [1957; rpt. New York: Dover, 1969], chap. 2. See also Howard Eves, An Introduction to the History of Mathematics [Fort Worth: Saunders College Publishing, 1992], pp. 44–47.)

1. This, however, is not a primitive triple, since it can be reduced to the simpler triple (28, 45, 53); the two triples represent similar triangles.

2. A fourth error occurs in line 2, where the entry 3,12,1 should be 1,20,25, producing the triple (3367, 3456, 4825). This error has remained unexplained.

3. As to how the Babylonians did the computations, see Neugebauer, Exact Sciences, pp. 39–42.