It is no coincidence that trigonometry up until the sixteenth century was developed mainly by astronomers. Aristarchus and Hipparchus, who founded trigonometry as a distinct branch of mathematics, were astronomers, as was Ptolemy, the author of the Almagest. During the Middle Ages, Arab and Hindu astronomers, notably Abul-Wefa, al-Battani, Aryabhata, and Ulugh Beg of Samarkand (1393–1449), absorbed the Greek mathematical heritage and greatly expanded it, especially in spherical trigonometry. And when this combined heritage was passed on to Europe, it was again an astronomer who was at the forefront: Johann Müller (see fig. 17).

Müller was born in Unfinden, near the town of Königsberg in Lower Franconia, in 1436 (this is not the more famous Königsberg—now Kaliningrad—in East Prussia). Different versions of his name survive: Johannes Germanus (because he was a German), Johannes Francus (because Franconia was also known as Eastern France), and Johann von Kunsperk, named after the town of Königsberg. Following the practice of scholars in his time he adopted a Latin name, Regio Monte, a literal translation of the German word “Königsberg” (“the royal mountain”), and in due time he was known as Regiomontanus. Even this name, however, exists in several versions: the French scientist Pierre Gassendi (Peter Gassendus, 1592–1655), who wrote the first definitive biography of Regiomontanus, refers to him as Joannes de Monte Regio, which has a distinctive French sound.¹

Regiomontanus spent his early years studying at home. When he was twelve his parents sent him to Leipzig for his formal education, and after graduating he moved to Vienna, getting his bachelor’s degree from its university at the age of fifteen. There he met the mathematician and astronomer Georg von Peurbach (1423–1461), with whom he formed a close friendship. Peurbach studied under Cardinal Nicholas of Cusa (1401–1464) but rejected the latter’s speculation that the earth might be moving around the sun. He was an admirer of Ptolemy and was planning to publish a corrected version of the Almagest, based on existing Latin translations. He also undertook the preparation of a new and more accurate table of sines, using the recently adopted Hindu-Arabic numerals. The young Regiomontanus quickly came under Peurbach’s influence, and the bonds between them reached the intensity of a father-to-son relationship. But then Peurbach suddenly died, not yet 38 years old. His untimely death left his plans unfulfilled and his pupil in a shock.

FIG. 17. A sketch of Regiomontanus.

On his deathbed Peurbach entrusted his young student to complete the translation of the Almagest. “This became a sacred trust for the fatherless student,” wrote Gassendi in his biography of Regiomontanus.² Regiomontanus completely dedicated himself to the task, learning Greek so that he could read Ptolemy in the original. In the course of his work he became interested in old Greek and Latin manuscripts and acquired them wherever he went; among his prizes was an incomplete manuscript of Diophantus which he discovered in 1464. He courted the friendship of many scholars, among them a Cretan, George of Trebizond (Georgius Trapezuntios, 1396–1486), an authority on Ptolemy who translated the Almagest and Theon’s commentaries on it into Latin. The friendship, however, turned sour when Regiomontanus criticized Trebizond for serious errors in his interpretation of the commentaries, calling him “the most impudently perverse blabber-mouth.”³ These words, by one account, would have dire consequences.

His many travels brought him to Greece and Italy, where he visited Padua, Venice, and Rome. It was in Venice, in 1464, that he finished the work for which he is best remembered, On Triangles of Every Kind (see below). In addition to all these activities, Regiomontanus was also a practicing astrologer, seeing no contradiction between this activity and his scientific work (the great astronomer Johannes Kepler would do the same two centuries later). Around 1467 he was invited by King Mathias Huniades Corvinus of Hungary to serve as librarian of the newly founded royal library in Budapest; the king, who had just returned victorious from his war with the Turks and brought back with him many rare books as booty, found in Regiomontanus the ideal man to be in charge of these treasures. Shortly after Regiomontanus’s arrival the king became ill, and his advisers predicted his imminent death. Regiomontanus, however, used his astrological skills to “diagnose” the illness as a mere heart weakness caused by a recent eclipse! Lo and behold, the king recovered and bestowed on Regiomontanus many rewards.

Regiomontanus returned to his homeland in 1471 and settled in Nürnberg, close to his birthplace. This city, known for its long tradition of learning and trade, had just opened a printing press, and Regiomontanus saw the opportunities it offered to spread the written word of science (it was just a few years earlier, in 1454, that Johann Gutenberg had invented printing from movable type). He founded his own press and was about to embark on an ambitious printing program of scientific manuscripts, but these plans were cut short by his early death. He also founded an astronomical observatory and equipped it with the finest instruments the famed Nürnberg artisans could produce; these included armillary spheres and devices for measuring angular distances between celestial objects.

Regiomontanus was the first publisher of mathematical and astronomical books for commercial use. In 1474 he printed his Ephemerides, tables listing the position of the sun, moon, and planets for each day from 1475 to 1506. This work brought him great acclaim; Christopher Columbus had a copy of it on his fourth voyage to the New World and used it to predict the famous lunar eclipse of February 29, 1504. The hostile natives had for some time refused Columbus’s men food and water, and he warned them that God would punish them and take away the moon’s light. His admonition was at first ridiculed, but when at the appointed hour the eclipse began, the terrified natives immediately repented and fell into submission.

In 1475 Pope Sixtus IV called upon Regiomontanus to come to Rome and help in revising the old Julian calendar, which was badly out of tune with the seasons. Reluctantly, he left his many duties and traveled to the Eternal City. And there, on July 6, 1476, he suddenly died, one month past his fortieth birthday. The cause of his death is not known: some blamed it on a plague, others on a passing comet. There were, however, persisting rumors that Regiomontanus was poisoned by Trebizond’s sons, who had never forgotten his stinging criticism of their father’s translation of Theon’s commentaries on Ptolemy.⁴ When news of his death became known, Nürnberg went into public mourning.⁵

Regiomontanus’s most influential work was his De triangulis omnimodis (On triangles of every kind), a work in five parts (“books”) modeled after Euclid’s Elements (fig. 18). In this work he organized into a systematic body of knowledge the trigonometric heritage of Ptolemy and the Hindu and Arab scholars. Book I begins with the definitions of basic concepts: quantity, ratio, equality, circle, arc, and chord. The sine function is introduced according to the Hindu definition: “When the arc and its chord are bisected, we call that half-chord the right sine of the half-arc.” Next comes a list of axioms, followed by fifty-six theorems dealing with geometric solutions of plane triangles. Much of this material deals with geometry rather than trigonometry, but Theorem 20 introduces the use of the sine function in solving a right triangle.

Trigonometry proper begins in Book II with the enunciation of the Law of Sines; as with all other rules, this is stated literally rather than in symbols, but the formulation is as clear as in any present-day textbook. The sine law is then used to solve the cases SAA and SSA of an oblique triangle. Here also appears for the first time, though implicitly, the formula for the area of a triangle in terms of two sides and the included angle: “If the area of a triangle is given together with the rectangular product of the two sides, then either the angle opposite the base becomes known, or [that angle] together with [its] known [exterior] equals two right angles.”⁶ In modern formulation this says that from the formula A = (bc sin α)/2 one can find either α or (180° – α) if the area A and the product of two sides b and c are given. Strangely, Regiomontanus never uses the tangent function, although he must have been familiar with it from Peurbach’s table of tangents of 1467, and of course from the Arabs’ use of it in connection with shadow reckoning.⁷

The remaining three books deal with spherical geometry and trigonometry, both necessary tools in astronomy. As he states in his introduction, Regiomontanus’s main goal in On Triangles was to provide a mathematical introduction to astronomy. In words that might have been taken from a modern textbook, he admonishes his readers to study the book carefully, as its subject matter is a necessary prerequisite to an understanding of the heavens:

FIG. 18. Title page of On Triangles of Every Kind (Nürnberg, 1533).

You, who wish to study great and wonderous things, who wonder about the movement of the stars, must read these theorems about triangles…. For no one can bypass the science of triangles and reach a satisfying knowledge of the stars…. A new student should neither be frightened nor despair…. And where a theorem may present some problem, he may always look down to the numerical examples for help.⁸

Regiomontanus completed writing On Triangles in 1464, but it was not published until 1533, more than half a century after his death. Through George Joachim Rhaeticus (1514–1576), the leading mathematical astronomer in Germany during the first half of the sixteenth century, it reached Nicolas Copernicus (1473–1543). Rhaeticus visited Copernicus in 1539 and became his first disciple; though Rhaeticus was younger than Copernicus by forty-one years, the two studied together, with the former instructing the latter in mathematics. (It was at Rhaeticus’s persistent prodding that Copernicus finally agreed to publish his great work, De revolutionibus, in which he expounded his heliocentric system.) He presented Copernicus with an inscribed copy of On Triangles, which the great master thoroughly studied; this copy survived and shows numerous marginal notes in Copernicus’s handwriting.⁹ Later, Tycho Brahe (1546–1601), the great Danish observational astronomer, used the work as the basis for calculating the position of the famous nova (new star) in Cassiopeia, whose appearance in 1572 he was fortunate to witness. Regiomontanus’s work thus laid much of the mathematical groundwork that helped astronomers shape our new view of the universe.

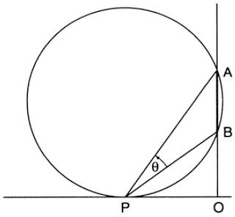
FIG. 19. Regiomontanus’s maximum problem: at what distance x will segment AB subtend the largest angle θ?

In 1471 Regiomontanus posed the following problem in a letter to Christian Roder, a professor at the university of Erfurt: “At what point on the ground does a perpendicularly suspended rod appear largest [i.e., subtends the greatest visual angle]?” It has been claimed that this was the first extreme problem in the history of mathematics since antiquity.¹⁰

In figure 19 let the rod be represented by the vertical line segment AB. Let OA = a, OB = b, and OP = x, where P is the point on the ground at which the angle θ = ∠BPA is maximum. Let α = ∠OPA, β = ∠OPB. We have

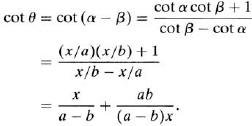
We might now be inclined to differentiate this expression in order to find the value of x that minimizes it (since cot θ is decreasing for 0° < θ < 90°, a maximum value of θ means a minimum value of cot θ). But Regiomontanus lived two hundred years before the invention of calculus, so let us restrict ourselves to elementary methods. We will use a theorem from algebra that says: the arithmetic mean of two positive numbers u and v is never smaller than their geometric mean, and the two means are equal if and only if the two numbers are equal. In symbols, , with equality holding if and only if u = v.¹¹ Putting u = x/(a – b), v = ab/(a – b)x, we have

FIG. 20. Geometric solution of Regiomontanus’s problem.

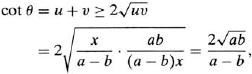
with equality holding if and only if x/(a – b) = ab/(a – b)x, that is, when . The required point is thus located at a distance equal to the geometric mean of the altitudes of the upper and lower endpoints of the rod, measured horizontally from the foot of the rod.

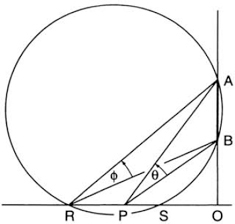
This result provides an interesting geometric interpretation: Using a straightedge and compass, construct the circle passing through A and B and tangent to the ground (fig. 20). By a well-known theorem, we have OA · OB = (OP)², that is, ab = x² and therefore . Conversely, we can easily convince ourselves that the circle passing through A, B, and the required point P must be tangent to the ground; for had it intercepted the ground at two points R and S (fig. 21), then the subtended angle at any point P between R and S would be greater than the angle at R or at S (P now being an interior point of the circle), whereas the angle at P was supposed to be the greatest. Thus Regiomontanus’s problem can be solved by a simple geometric construction.¹²

FIG. 21. Proof of the geometric solution.

We can only speculate what prompted Regiomontanus to propose this problem. It may have originated as a problem in architecture or perspective: to find the most favorable position from which to view a window of a tall building. Perspective—the technique of drawing objects according to their true appearance to the eye—was then a novel subject, introduced by the Italian Renaissance artists Filippo Brunelleschi (1377–1446) and Leone Battista Alberti (1404–1472). (The famed artist Albrecht Dürer, a major writer on perspective, was born in Nürnberg the year Regiomontanus settled there.) It soon became a central doctrine in art, and its juxtaposition of two seemingly alien disciplines—art and geometry—was in tune with the Renaissance ideal of universalism. It may well be that Regiomontanus posed his problem in response to an inquiry from an artist or architect.

NOTES AND SOURCES

1. See Regiomontanus on Triangles, translated by Barnabas Hughes with an introduction and notes (Madison: University of Wisconsin Press, 1967), pp. 11–17, from which this biographical sketch is adapted. See also David Eugene Smith, History of Mathematics (1923; rpt. New York: Dover, 1958), vol. 1, pp. 259–260. The only modern biography of Regiomontanus is in German: Ernst Zinner, Leben und Wirken des Johannes Müller von Königsberg genannt Regiomontanus (Munich: C. H. Beck, 1939).

2. As quoted in Hughes, Regiomontanus on Triangles, p. 13.

3. Ibid., p. 14.

4. The story about his death by poisoning is told in Gassendi’s biography of Regiomontanus, dated 1654, and evokes echoes of Antonio Salieri allegedly poisoning his arch rival, Mozart.

5. The French humanist Peter Ramus (Pierre de la Ramée, 1515–1572) attributed to Regiomontanus the invention of a mechanical fly that could leave a person’s hand, buzz about the room, and then return to the person’s hand, and an eagle that could leave the city, fly to meet an approaching dignitary, and then accompany him back to the city. (Hughes, Regiomontanus on Triangles, p. 17). These stories are no doubt an exaggeration, but they reflect the high esteem with which Regiomontanus was held by his fellow townsmen. In Ramus’s words, “Tarento had its Archytas, Syracuse its Archimedes, Byzantium Proclus, Alexandria Ctesibius, and Nürnberg Regiomontanus…. The mathematicians of Tarento and Syracuse, of Byzantium and Alexandria are gone. But among the Masters of Nürnberg, the joy of the scholars is the mathematician Regiomontanus.”

6. Ibid., p. 133.

7. Ibid., pp. 4–7.

8. Ibid., pp. 27–29.

9. Ibid., p. 9.

10. Heinrich Dörrie, 100 Great Problems of Elementary Mathematics: Their History and Solution, translated by David Antin (1958; rpt. New York: Dover, 1965), pp. 369–370. I have slightly changed the wording so as to make the reading easier.

11. This theorem follows from the fact that the square of a real number can never be negative; hence . Moving the term to the left side and dividing by 2, we get the required result. Equality occurs if and only if , i.e., u = v.

12. I was unable to find out if Regiomontanus actually provided a solution. According to Florian Cajori (A History of Mathematical Notation, 1928; rpt. La Salle, Ill.: Open Court, 1951, vol. 1, p. 95), Regiomontanus’s correspondence with fellow scientists during the period 1463–1471 is preserved at the Stadtbibliothek of Nürnberg.