11

A Remarkable Formula

The prototype of all infinite processes is repetition…. Our very concept of the infinite derives from the notion that what has been said or done once can always be repeated.

—Tobias Dantzig, Number: The Language of Science

We are not quite done yet with the function (sin x)/x Browsing one day through a handbook of mathematical formulas, I came across the following equation:

As I had never seen this formula before, I expected the proof to be rather difficult. To my surprise, it turned out to be extremely simple:

After repeating this process n times, we get

sin x = 2ⁿ sin x/2ⁿ · cos x/2ⁿ ·… · cos x/2.

Let us multiply and divide the first term of this product by x (assuming, of course, that x ≠ 0) and rewrite it as x · [(sin x/2ⁿ)/(x/2ⁿ)]; we then have

Note that we have reversed the order of the remaining terms in the (as yet finite) product. If we now let n → ∞ while keeping x constant, then x/2ⁿ → 0 and the expression in the brackets, being of the form (sin α)/α, will tend to 1. We thus have

where Π stands for “product.” Dividing both sides by x, we get equation (1).

Equation (1) was discovered by Euler¹ and represents one of the very few examples of an infinite product in elementary mathematics. Since the equation holds for all values of x (including x = 0, if we define (sin0)/0 to be 1), we can substitute in it, for example, x = π/2:

Now sin π/2 = 1 and cos π/4 = (√2)/2. Using the half-angle formula cos for each of the remaining terms, we get, after a slight simplification,

This beautiful formula was discovered by Viète in 1593; in establishing it he used a geometric argument based on the ratio of areas of regular polygons of n and 2n sides inscribed in the same circle.² Viète’s formula marks a milestone in the history of mathematics: it was the first time an infinite process was explicitly written as a succession of algebraic operations. (Up until then mathematicians were careful to avoid any direct reference to infinite processes, regarding them instead as a finite succession of operations that could be repeated as many times as one wished.) By adding the three dots at the end of his product, Viète, in one bold stroke, declared the infinite a bona fide part of mathematics. This marked the beginning of mathematical analysis in the modern sense of the word.

Aside from its beauty, Viète’s formula is remarkable because it allows us to find the number π by repeatedly using four of the basic operations of arithmetic—addition, multiplication, division, and square root extraction—all applied to the number 2. This can be done even on the simplest scientific calculator:

(on some calculators the memory operations STO, RCL, and SUM are labeled M, RM and M+, respectively). At each iteration you can read the current approximation of π by pressing the 1/x key immediately after × in the key sequence shown above; then press 1/x again to start the next iteration. It is fascinating to watch the numbers in the display gradually approach the value of π; after the ninth iteration we get 3.1415914—a value correct to five places. A programmable calculator, of course, will speed up things considerably.

It is instructive to examine equation (1) from the point of view of convergence. We note, first of all, that the convergence of the partial products to their limiting value is monotonic; that is, each additional term carries us closer to the limit. This is because each term is a number less than 1, causing the value of the partial products to continually diminish. This is in marked contrast to the infinite series for (sin x)/x,

which approaches its limit alternately from above and below. The convergence, moreover, is very fast, although it is somewhat slower than that of the series. Table 5 compares the rates of convergence of equations (1) and (2) for x = π/2:

TABLE 5

Note: All figures are rounded to four decimal places.

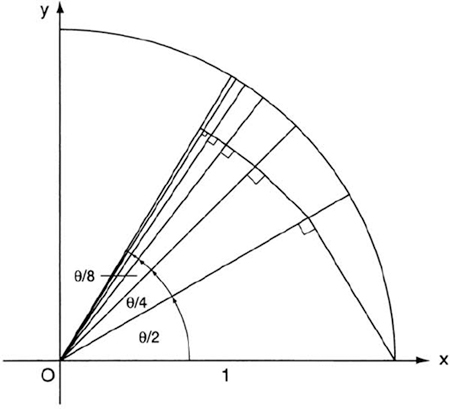
The reason for the rapid convergence of the infinite product can be seen from figure 68. On the unit circle we mark off the radii corresponding to the angles θ/2, (θ/2 + θ/4), (θ/2 + θ/4 + θ/8), and so on. These angles form an infinite geometric progression whose sum is θ/2 + θ/4 + θ/8 + ··· = θ. Now, beginning at the x-axis, we take the perpendicular projection of each radius on the next radius. The lengths of these projections are 1, cos θ/2, cos θ/2 · cos θ/4, cos θ/2 · cos θ/4 · cos θ/8, and so on. We see that after only a few steps the projections become barely distinguishable from their final value.

FIG. 68. Convergence of the infinite product

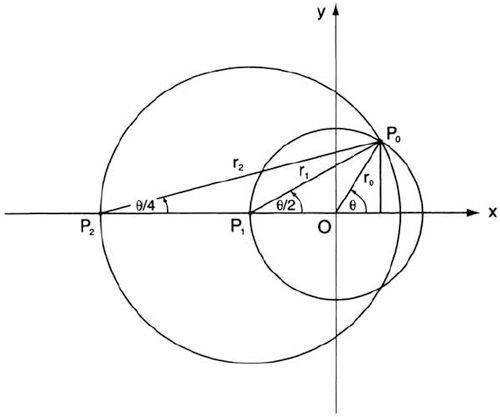
Following the principle that every trigonometric identity can be interpreted geometrically, we now ask what geometric meaning we can give to equation (1). The answer is given in figure 69. We start with a circle of radius r₀ centered at the origin. From the x-axis we mark off an angle θ, whose terminal side intercepts the circle at the point P₀. We now connect P₀ with the point P₁ whose coordinates are (–r₀, 0) and denote the segment P₁ P₀ by r₁. Angle OP₁P₀, having its vertex on the circle through P₁ and subtending the same arc as θ, is equal to θ/2. Applying the Law of Sines to the triangle OP₁P₀, we have

But sin(180° – θ) = sin θ = 2 sin θ/2 · cos θ/2; putting this back in equation (3) and solving for r₁, we get r₁ = 2r₀ cos θ/2.

We now draw a second circle, having P₁ as center and r₁ as radius. We have ∠OP₂P₀ = θ/4, so that a repetition of the steps just performed and applied to the triangle P₁P₂P₀ gives us r₂ = 2r₁ cos θ/4 = 4r₀ cos θ/2 · cos θ/4, where r₂ = P₂P₀. Repeating this process n times, we get a circle with center at P_n and radius

FIG, 69. Geometric proof of the formula

r_n = P_nP₀ given by

Now ∠OP_nP₀ = θ/2ⁿ, so that the Law of Sines applied to the triangle OP_nP₀ gives us r₀/(sin θ/2ⁿ) = r_n/sin(180° – θ); hence

Eliminating r₀ and r_n between equations (4) and (5), we get

As n increases without bound, angle ∠OP_nP₀ approaches zero and thus becomes indistinguishable from its sine; in other words, the arc whose radius is r_n tends to the perpendicular from P₀ to the x-axis. Replacing, then, sin θ/2ⁿ by θ/2ⁿ and canceling the factor 2ⁿ, we get equation (1), with θ instead of x.

Thus equation (1) is the trigonometric manifestation of the theorem that an angle inscribed in a circle has the same measure as one-half the central angle subtending the same arc, repeated again and again for ever smaller angles inscribed in ever larger circles.³

NOTES AND SOURCES

(This chapter is based on my article, “A Remarkable Trigonometric Identity,” Mathematics Teacher, vol. 70, no. 5 (May 1977), pp. 452–455.)

1. E. W. Hobson, Squaring the Circle: A History of the Problem (Cambridge, England: Cambridge University Press, 1913), p. 26.

2. See Petr Beckmann, A History of π (Boulder, Colo.: Golem Press, 1977), pp. 92–96.

3. A proof of equation (1) based on physical considerations is given in the article mentioned above.