Chapter 11

Poisson Processes — A Probabilistic and
Statistical Study

11.1. Introduction

A Poisson process models a sequence of events that occur at random instants.

Let 0 < T1 < T2 < … < Tn < … be the arrival time of a sequence of events such that limn↑ ∞ Tn = + ∞. For reasons that will be apparent later, we set T0 = 0.

Supposing the Tn to be random variables defined on the same probability space, is said to be a point process.

Equivalently, the process may be defined, where Nt denotes the number of events that occur in the interval [0, t]. We say that (Nt) is the counting process associated with (Tn).

(Nt) and (Tn) are connected by the following relations:

– N0 =T0 = 0;

–

– {Nt = n} = {Tn ≤ t < Tn + 1};

– {Nt ≥ n} = {Tn ≤ t};

– {s < Tn ≤ t} = {Ns < n ≤ Nt}.

Consequently, (Nt) is entirely determined by (Tn), and vice versa.

11.2. The axioms of Poisson processes

To specify the distribution of the process, we make the following hypotheses:

  A1: (Nt, t ≥ 0) has independent increments, i.e. N_t2 − N_t1 ,…, N_tk − N_tk−1 are independent for all k > 2, 0 ≤ t1 < t2 < … < tk.

  A2: (Nt, t ≥ 0) has stationary increments, i.e. P(Nt + h − Ns + h) = P(Nt − Ns) for 0 ≤ s < t, h > 0.

THEOREM 11.1.– Under A1 and A2, there exists a real number λ > 0 such that for all s < t, Nt − Ns follows the Poisson distribution with parameter λ(t − s):

λ is called the intensity of a (homogeneous) Poisson process (Nt).

PROOF.–

1) Let gs − t be the generating function of Nt − Ns:

The decomposition Nt = (Nt − Ns) + (Ns − N0) and axioms A1 and A2 lead to

[11.1]

Therefore, for rational t,

[11.2]

and since gt(u) ∈ [0, 1], [11.1] implies the decrease of t gt(u) and [11.2] remains valid for irrational t.

Moreover, gt(u) does not vanish, as gt0(u) = 0 would lead to g1(u) = 0, from [11.2], hence gt(u) = 0 for all t > 0, which contradicts

Consequently,

[11.3]

with λ(0) ≠ 0, as otherwise gt(0) = 1 for all t > 0; therefore, 1 = P(Nt = 0) = P(T1 > t), t > 0, hence T1 = +∞ a.s.

2) To identify λ(u), we will first show that:

[11.4]

For this, we write

Since P(Nt = 0) = gt(0) = e−tλ(0), we have:

that is

Since P(T2 ≤ T1) = 0 and 1 − e−hλ(0) ~ hλ(0), we deduce [11.4].

3) Now

and, from part (2),

therefore

where λ is constant and defined by λ = limh↓0 P(Nh = 1)/h.

Finally,

which is the generating function of the Poisson distribution with parameter λt.

COMMENT 11.1 During the proof, we showed that:

− P(Nt + h − Nt = 0) = 1 − λh + o(h);

− P(Nt + h − Nt = 1)=λh + o(h);

− P(Nt + h − Nt ≥ 2)= o(h).

Thus, for small h, Nt + h − Nt approximately follows a Bernoulli distribution with parameter λh.

11.3. Interarrivai time

Let us set Wn = Tn − Tn − 1, n ≥ 1. Then:

THEOREM 11.2.– The random variables Wn, n ≥ 1, are independent and follow the exponential distribution with parameter λ:

PROOF.– It is sufficient to establish the relation

[11.5]

This is true for n = 1 as

For simplicity, [11.5] will now be shown for n = 2, but the proof is completely analogous for any n.

For s1 < t1 < s2 < t2, we have:

Therefore, (T1, T2) has the density

Now, T1 = W1 and T2 = W1 + W2; therefore, the change of variables y1 = w1 and y2 = w1 + w2 gives the density of (W1 W2), i.e. .

COROLLARY 11.1.– Tn follows the Gamma distribution T(n, λ) with density:

PROOF.– Let us consider the identity

By differentiation, we obtain:

COMMENT 11.2.– We may also use the formulas

where * denotes the convolution, and

Moments of Tn: From Corollary 11.1, we have ETn = n/λ and VarTn = n/λ2.

We now establish the converse of Theorem 11.2:

THEOREM 11.3.– Let (Tn, n ≥ 0) be a point process such that the random variables Wn = Tn − Tn − 1, n ≥ 1, are independent and have the same exponential distribution with parameter λ. Then the associated counting process is a Poisson process with intensity λ.

PROOF.– (W1, …, Wn) has the density . By making the change of variables:

we obtain the density of (T1, …, Tn):

To avoid ungainly calculations, we will simply determine the distribution of (Ns, Nt − Ns), t > s:

However,

and moreover, the Lebesgue measure being invariant under translation,

Similarly,

and finally:

Thus, a Poisson process may be characterized by one of the following conditions:

  C1:

  C2:

11.4. Properties of the Poisson process

THEOREM 11.4.– If (Nt) is a Poisson process with intensity λ:

where (U(1), …, U(k)) denotes the order statistic associated with the U1, …, Uk, which are independent and have the same uniform distribution on [0, t].

PROOF.– We show that the density of (U(1), …, U(k)) at the point (u(1), …, u(k)) is written as:

Now, we write for 0 < t1 < t1 + h1 < t2 < … < tk + hk < t:

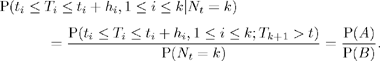
We saw that (T1, …, Tk + 1) follows the distribution with density therefore

Successively integrating, we obtain:

Hence,

Taking the limit, after dividing by h1 … hk, we obtain the stated result.

COMMENT 11.3.– It may also be shown that:

Now, for fixed s > 0, we define a new point process by considering the arrival time

The associated counting process is written as:

It clearly defines a Poisson process with intensity λ. From is independent of (Nt, 0 ≤ t ≤ s).

It may be shown that this property remains when we replace the constant time s with a random time S which depends only on the past (i.e. for t ≥ 0 the event only depends on the random variables Ns, s ≤ t).

S is then said to be a stopping time and we set:

Note that a constant time is a stopping time.

THEOREM 11.5. Markovian property of the Poisson process.– If (Nt, t ≥ 0) is a Poisson process with intensity λ, and if S is a stopping time, then is a Poisson process with the same intensity, and is independent of (N_s, s ≤ S).

The above theorem demonstrates a crucial property of Poisson processes: follows the distribution e(λ), therefore Tn − Tn − 1 and T_Ns+1 −T_Ns do not have the same distribution.

EXAMPLE 11.1. The waiting time paradox.– If, at the instant s, a customer arrives at a station where buses stop every m minutes, their waiting time τ follows a uniform distribution on [0, m]; therefore,

When there is traffic, the arrivals of buses may be modeled using a Poisson process with intensity 1/m. Then, we have E(Tn − Tn − 1) = m, but τ = T_Ns+1 − s follows an exponential distribution with parameter 1/m, and consequently

Therefore, on average, the waiting time is doubled.

11.5. Notions on generalized Poisson processes

1) Non-homogeneous Poisson processes

In practice, the intensity often varies with time; for example, the interarrival time of calls to an exchange has different distributions at various periods during the day.

(Nt, t ≥ 0) is said to be a non-homogeneous Poisson process if its increments are independent and if:

It may then be shown that Nt follows a Poisson distribution with parameter

COMMENT 11.4.– By changing the time, (Nt) may be transformed into a homogeneous Poisson process. For this, we set:

where m−1 is the generalized inverse of m defined by:

(Mt) is then a (homogeneous) Poisson process with intensity 1.

2) Compound Poisson processes

Let (Nt) be a Poisson process and (Yn) be a sequence of independent random variables with the same distribution. (Nt) and (Yn) are assumed to be independent and we set, for t ≥ 0:

[11.6]

(Xt) is then said to be a compound Poisson process.

EXAMPLE 11.2.–

   1) The holders of an insurance policy are victims of misfortunes at the instants 0 < T1 < T2 < … following a Poisson process with intensity λ. They obtain the respective payments Y1, Y2, … The total payment Xt at time t satisfies [11.6].

   2) A particle is subjected to impacts at the Poissonian instants Tn, and Yn denotes the displacement of the particle at time Tn. Xt denotes the position of the particle at time t(X0 = 0): (Xt) is a compound Poisson process.

When the intensity λ tends to infinity, by taking the limit in distribution, a Wiener process is obtained (see Chapter 12).

3) Multidimensional Poisson processes

Let E be a Borel set on is a family of integer-valued random variables, indexed by , the set of bounded Borel sets of E.

Let m be a measure on that is finite on is said to be a Poisson process of mean measure m if:

   1) .

   2) are disjoint, and the random variables are independent.

If and if m = λμ where μ is the Lebesgue measure on , we find the homogeneous Poisson process defined at the beginning of this chapter.

11.6. Statistics of Poisson processes

1) The observation of a Poisson process may be carried out in several ways. For example, the arrival times on the interval [0, t] may be observed, or the process may be observed until n events are realized.

In the first case, the observations may be written as T₀, T₁,…, T_Nt.

Yet, from Theorem 11.4, the conditional distribution of the observations given Nt does not depend on the unknown paramater λ. This means that Nt contains all of the information about λ, and is therefore a sufficient statistic.

Now, if T1, …, Tn have been observed, the equality

shows that Tn is a sufficient statistic.

It is therefore sufficient to know Nt (or Tn) to have all of the information contained in the data.

2) Estimation of λ

From the above, we may suppose that only Nt (or Tn) is observed.

The likelihood of Nt is written as:

Hence, the maximum likelihood estimator:

This estimator is unbiased (i.e. ) and is the only estimator with this property. Indeed, if there existed some ψ(Nt) such that:

we would have:

By making explicit this expectation, we would deduce that:

which defines a power series in λ, which has an infinite radius of convergence and is identically zero. Consequently,

THEOREM 11.6.– When t tends to infinity, tends almost surely and in quadratic mean to λ, and converges in distribution to the standard normal distribution.

PROOF.– The convergence in quadratic mean is clear, since

For the a.s convergence, we consider the inequalities:

[11.7]

where [·] denotes the integer part.

Since

the strong law of large numbers leads to

Similarly, we have:

and from [11.7]

For the convergence in distribution, we use the decomposition:

Since , the central limit theorem states that At converges in distribution to ; Tchebychev’s inequality shows that Bt converges in probability, and therefore in distribution, to 0. Since At and Bt are independent, the continuity of convergence in distribution with respect to convoluion leads to the convergence in distribution of .

Now, from Corollary 11.1, Tn follows the distribution Γ(n, λ); hence its likelihood:

Maximizing this, we deduce the estimator:

This estimator is biased, as

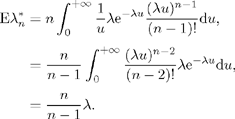
Consequently, (n − 1) /Tn is unbiased, and, using the uniqueness of the Laplace transform, it may be shown that it is the only estimator with this property.

A simple calculation shows that:

Finally, the decomposition and the strong law of large numbers implies that .

3) Confidence intervals and tests on λ

A confidence interval based on is generally obtained by normal approximation.

Let α ∈ ]0, 1[ and υ1 − α be such that P(|N| < v1 − α) = 1 − α where . Then:

The error introduced by replacing with may be considered to be negligible. From this, we deduce the confidence interval of (approximate) size 1 − α:

If we wish to use , it is sufficient to note that 2λTn follows a χ2 distribution with 2n degrees of freedom, then let qβ be such that P(2n > qβ) = β where 2n ~ χ2(2n). Since P(q1 − β/2 < 2λTn < qβ/2) = 1 − β, we obtain a confidence interval with size 1 − β:

The hypothesis tests on λ are based on the same principles.

For example, if Nt is observed and we seek to verify that λ = λ0, we may use the test consisting of accepting this hypothesis if:

and rejecting it otherwise. This test is of asymptotic size α.

If Tn is observed and if we wish to test the hypothesis 0 < λ ≤ λ0, the rejection region will be of the form:

To determine c, we write the equation:

and, using 2λ0Tn ~ χ2(2n), we find that:

that is

This test is of size α.

The common values of α are 1% and 5%.

Finally, the general results from the theory of hypothesis testing show that these tests have optimality properties.

4) Verifying the Poisson hypothesis

Given a point process observed on the interval [0, t], we seek to verify that it acts as a homogeneous Poisson process. For this, we may use the converse of Theorem 11.4, testing the uniformity of the distribution of the Ti given that Nt = n.

One such test is based on a deviation between the uniform distribution μ on [0, t] and the empirical distribution of the Ti defined by where δ_(·) denotes a Dirac measure.

The common deviations are:

where k is given.

It may be shown that for n tending to infinity:

(see Chapter 8.)

From this, we deduce certain tests whose region of rejection is of the form with . The distributions of K, W, and are tabulated.

Comparing the efficiency of these tests poses a difficult problem. However, it seems that the tests based on Dn and Wn are superior to the χ2 test.

For a detailed discussion, we refer to [COX 69].

5) Comparing two Poisson processes

Let us consider two independent Poisson processes with intensities λ and λ′, and respective arrival times Ti and .

We wish to test the hypothesis λ′ = λ from the observations and .

Since and , we deduce that if λ′ = λ, then follows a Fisher distribution with (2n1, 2n2) degrees of freedom F(2n1, 2n2).

Hence, the test:

with

Note that this test may also be used to verify the homogeneity of a Poisson process observed on two disjoint intervals of time.

11.7. Exercises

EXERCISE 11.1.– Customers arrive at a shop at a mean rate of 3 per minute. The arrival times follow a Poisson process.

1) Calculate the probability that a single customer arrives every 2 min.

2) Calculate the probability that no customers arrive for 5 min.

3) Calculate the probability that in two disjoint periods of 2 min, at least two customers arrive.

EXERCISE 11.2.– The arrival times of a shop’s customers are Poissonian, and they occur at a rate of 30 per hour. We count in minutes, and we write {Wn}n ≥ 1 the interarrivai times. Calculate:

EXERCISE 11.3.– A particle counter only counts half the particles arriving at the counter. We suppose that the particles arrive according to a Poisson process, with a mean rate of 4 per minute. Let S be the waiting time between two recorded particles.

1) Calculate the distribution of S, ES, Var(S).

2) Calculate P(S > 1).

EXERCISE 11.4.– Let , be the arrival time associated with a Poisson process with parameter λ, and let B be a bounded Borel set of . We introduce the random variable:

Determine the distribution of NB.

Hint: You may write

EXERCISE 11.5.– We consider the positive random variables , defined on the same space , identically distributed, cumulative distribution function F.

The results of this exercise may be interpreted, for example, from the viewpoint a hitchhiker who, placed at one point of a road, observes that the time Xi elapses between the passing of the (i − 1)th car and the ith car. If the traffic is fluid, we may consider, as a first approximation, that the are independent and have an exponential distribution.

1) We set:

Interpret these variables, noting that

2) Let Wt be the time that the hitchhiker must wait, starting from the time t, to see a car pass, and let Z_t = t − T_Nt.

   i) What is Wt + Zt?

   ii) Give the distribution of the pair (Wt, Zt), showing that these two distributions are independent, that Wt follows an exponential distribution with parameter θ, and that Zt has the same distribution as min(X1, t).

   iii) Show that Zt converges in distribution to X1 when t tends to infinity.

EXERCISE 11.6.– are Poisson processes with intensities λ1 and λ2, which we assume to be independent. What is the nature of the process ?

EXERCISE 11.7.– Let , be two independent Poisson processes, with respective parameters λ1 and λ2. We suppose that λ1 ≠ λ2. We set

1) Show that the increments of the process are independent and stationary.

2) Give the distribution of Xt − Xs, t > s.

3) Calculate limt→+∞ P(|Xt| ≤ c).

4) Supposing to be the number of customers arriving at a taxi stand, and to be the number of taxis arriving there, what does Xt represent? How is the result of question (3) interpreted? Why is this model unrealistic?

EXERCISE 11.8.– Some particles have the probability of 2/3 of striking a target. They arrive following a Poisson process, at a rate of 6 per minute. Let Xt be the number of particles that strike the target between 0 and t. Give the expressions of:

EXERCISE 11.9.– is a compound Poisson process. is centered and has the variance σ2 > 0. Give the characteristic function of and the limit in distribution of this variable when λ tends to infinity.

EXERCISE 11.10.– We are interested in modeling a waiting line (the queue at a service window, etc.). We suppose that some customers 0, 1, …, n, …, arrive to queue at a service window with interarrivai times A0 = 0, A1, …, An, …, the nth customer arriving at the time A0 + A1 + … + An. The are independent and identically distributed (i.i.d.) random variables that take values from .

We write as B0, B1, …, Bn, … some real, i.i.d. random variables on , which represent the service times: the agent at the window takes Bn units of time to attend to the nth customer after which he passes immediately to attend the (n + l)th customer.

We write Wn for the time separating the arrival time of the customers in the line and their arrival time at the window (i.e. when they begin to be attended to). We have W0 = 0.

1) Give the time at which the agent finishes serving the nth customer. Deduce that the satisfy the recurrence relation:

2) We set Xn = Bn − 1 − An, S0 = 0, Sn = X1 + … + Xn (n ≥ 1). Show by induction that:

From this, deduce that .

3) We study the asymptotic behavior of Wn. We suppose that A1 and B1 have expected values, and we set:

Show that if ρ > 1, then Sn tends (a.s.) to + ∞. What is the consequence of this result for the limit in distribution of Wn? What about the overcrowding of the waiting line?

Show that if ρ < 1, then Sn tends (a.s.) to −∞. Deduce that is finite (a.s.). What is the consequence of this for the waiting line?

Do these results seem intuitively apparent to you?

EXERCISE 11.11.– A device records signals that occur at the instants 0 < T1 < T2 < … < Tn < … following a Poisson process with intensity λ. These signals have the respective intensities I1, I2, …, In, …, which are random, independent, and have the same distribution with density where θ > 0. The two sequences (Tn) and (In) are independent. At each instant Tj, the signal is recorded if and only if Ij > x0 where the threshold x0 > 0 is fixed.

1) Let (Nt) be the counting process of (Tn) and () be the counting process associated with the sequence of recorded signals. Determine

and deduce that follows a Poisson distribution with parameter .

2) What is the distribution of (N′s, − N′s), 0 ≤ s < t?

3) Show that () is a Poisson process, given its intensity μ.

4) Construct the maximum likelihood estimator of μ when () is observed on the interval [0, n].

5) Suppose that, further to the previous observations, we make use of the observation of some signals on the interval [n, 2n] using a second device that records the signals as soon as their intensity passes X0/2. Construct an estimator of (θ, λ); X0 is assumed to be known.

6) Show the almost sure convergence of when n tends to infinity.

EXERCISE 11.12.–

1) Show that a Poisson process has the same covariance function as a Wiener process (see Chapter 12), and prove that it is continuous in quadratic mean. Are the trajectories of a Poisson process continuous?

2) Prove that if {Nt, t ≥ 0} is a Poisson process with parameter 1, then we have:

defining the mode of convergence, where is a weak white noise with variance 1.

EXERCISE 11.13.– , denote discrete, positive variables that count events of type 1 or type 2. We make the following hypotheses:

Supposing that there exists an obeying the hypotheses H1 and H2, we write

1) Show that:

2) Deduce that the generating function of Nt satisfies:

Determine this generating function.

3) What are the distributions of and ? What happens when v = 0?