Chapter 13

Stochastic Integration and Diffusion Processes

13.1. Itô integral

Let (Wt, t ≥ 0) be a standard Wiener process with basis space , and be the class of random functions f such that:

1) , where λ is the Lebesgue measure on [a, b].

2) ∀t ∈ [a, b], f(t,·) is -measurable (i.e. f is nonanticipative with respect to W).

We propose to define an integral of the form:

We begin by defining the integral on the set of step functions belonging to :

where the intervals [ti,ti+1) are open on the right, except for the last, and fi is -measurable for all i.

We set:

LEMMA 13.1.–

1)

2)

PROOF.–

1)

(We used the -measurability of fi and the fact that (Wt) has independent increments.)

2) Let us first note that we may represent f and g using the same partition of [a, b]. Then

Now is a closed linear subspaceof L2 equipped with the usual scalar product:

Then is a linear mapping from to L2 , which preserves the scalar product.

Therefore, it has a unique extension that has the same properties. We will see that , which allows us to define the integral on all of .

LEMMA 13.2.–.

PROOF.–

1) contains the f such that t f(t, ·) is (uniformly) continuous on [a, b] in L2 . Indeed, if f is such a function, one may set:

and

may be made arbitrarily small for a convenient choice of the ti.

2) If f is bounded, then . To show this, we set:

then from condition (1) of section 13.1, and (fn) → f in L2([a, b] × Ω), therefore .

The details of the proof may be found in [ASH 75].

We may now state:

THEOREM 13.1.– , has one unique extension to that is linear, continuous, and such that:

fdW is called the stochastic integral or the Itô integral of f.

PROPERTIES.–

1) Integration by parts: If f is non-random, and of class C1, we have:

where the last integral is in mean square (Chapter 12).

2) Properties of

   i) A modification of (Xt) (i.e. such that a.s.) may be found, which is progressively measurable (i.e. (s, ω) Ys (ω) is measurable with respect to ).

   ii) Almost every sample path of (Xt) is continuous and (Xt) is continuous in quadratic mean.

   iii) (Xt, a ≤ t ≤ b) is non-anticipative.

   iv) (Xt) is a martingale:

For proofs, we refer to [ASH 75].

13.2. Diffusion processes

To model the drift of a particle immersed in a moving, non-homogeneous fluid, we consider the stochastic differential equation:

[13.1]

where Wt is a standard Brownian motion process.

INTERPRETATION 13.1.– Xt is the abscissa of the particle’s position, and m(x,t) is the velocity of a small volume υ of the fluid located at x at time t. A particle situated inside υ undergoes Brownian motion with coefficient σ(x, t). dXt is the abscissa of the displacement of the particle in the small time interval dt.

To be precise, [13.1] mathematically means:

[13.2]

where the first integral is in mean square and the second is an Itô integral.

To establish that [13.2] has a solution, we make the following hypotheses:

– m and σ are measurable and Lipschitz functions:

– Furthermore

– Finally, , where .

COMMENT 13.1.– If (L) is satisfied, (M) is equivalent to t m(0, t) and t σ(0, t) being bounded on [a, b].

THEOREM 13.2.– Under the previous hypotheses, there exists a (Xt,a ≤ t ≤ b) such that:

1) (Xt) .

2) (Xt) is continuous in mean square and has (a.s.) continuous trajectories.

3) (Xt) is a solution of [13.2] with initial condition Xa.

4) (Xt) is unique in the sense that if (Yt) is a solution of [13.2] that satisfies Ya = Xa, then

PROOF.–

1) We recursively define:

Let us show by induction that (Xn(t),a ≤ t ≤ b) satisfies (1), (2) and (2′): .

This property is apparent for (X0(t)).

To establish continuity in mean square, we write:

Yet

and

therefore

and from (M)

Since Xn−1 is continuous in mean square, it is bounded in L2 norm, and consequently In → 0 when t → s.

The trajectories of Xn are (a.s.) continuous, as the stochastic integral has continuous trajectories and Xn−1 is bounded.

that is (a.s.) bounded, as Xn has continuous trajectories and

therefore (2′) is satisfied.

Since Xn−1 is non-anticipative, so too is Xn (a property of integrals). We saw above that Xn ∈ L2(λ ⊗ P).

2) We now show that:

For this, we set:

Then

Bounding the above equation, as previously, gives:

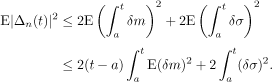
Hence, using (L), we obtain:

where A = 2((b − a) + l)k2.

In particular

and by immediate induction

Yet

and the upper bound tends to 0 when n and m tend to infinity.

(Xn(t), n ≥ 0) is therefore a Cauchy sequence: it converges in mean square to a random variable X(t). This convergence is uniform on t, since the upper bound does not depend on t.

3) Properties of (Xt, a ≤ t ≤ b)

(X(t)) is non-anticipative as is (Xn(t)). Moreover, the uniform convergence of (Xn(t)) to (X(t)) leads to the mean square continuity of (X(t)). Consequently, is bounded on [a, b], hence .

Finally, (X(t)) is a solution to [13.2] as X(a) = lim Xn (a) = Xa and, if we set:

then

The first term in square brackets tends to 0 in mean square; this is also the case for both integrals as, according to hypothesis (L), they are an (sups E | X (s) − Xn (s) |2 ).

Finally, [13.2], and the properties of integrals, assure the continuity of the trajectories.

4) Uniqueness

Write:

With the same reasoning as before, we obtain:

Hence

that is

e−At F(t) is then positive, decreasing, zero at a and therefore identically zero: P(X_t = y_t) = 1, a ≤ t ≤ b.

Thus

from which we find the result using the continuity of the trajectories.

Itô’s formula

The following formula allows the transformation of a process satisfying a stochastic differential equation. Suppose that:

a ≤ t ≤ b, where is continuous and has the continuous derivatives and .

Then (Yt) satisfies the stochastic differential equation:

where

and

The proof of Itô’s formula may be found in [ASH 75], pp. 227-230.

13.3. Processes defined by stochastic differential equations and stochastic integrals

EXAMPLE 13.1.–

1) Xt = mt + σWt, t ≥ 0, where m and σ > 0 are constant, and (Wt) is a standard Wiener process. Thus

2) The Black–Scholes model: this model is defined by the stochastic differential equation:

where m and σ are non-random and the conditions of the existence theorem are assumed to be satisfied.

Let us set:

and

then Y0 = 0, and from Itô’s formula:

Consequently

hence

For X0 = 1, m(t) ≡ m, σ(t) ≡ σ, the (simple) Black–Scholes model is found:

Note that Xt follows a log-normal distribution: log Xt has the distribution

More precisely, (log Xt) is, up to a transformation, a Wiener process since

Furthermore, since

we have, when t → + ∞:

The Black–Scholes model is used in finance.

3) Purely non-deterministic Gaussian processes: these are of the form

where g is non-random, zero on , and square-integrable on

(Wt, ) is a bilateral Wiener process defined by considering two independent standard Wiener processes (), i = 1, 2, and setting

Finally, the integral is defined from the Itô integral on a compact interval by taking a convenient limit.

(Xt, ) is Gaussian, centered, stationary, and has autocovariance

[13.3]

These processes are analogous to purely non-deterministic discrete-time stationary processes, i.e. processes of the form:

One important particular case is the Ornstein–Uhlenbeckprocess defined by:

[13.4]

This process is a solution to the stochastic differential equation:

Indeed, posing Yt = e+θt Xt, Itô’s formula gives:

Hence

that is

Making t tend to − ∞, we obtain [13.4].

The Ornstein–Uhlenbeck process provides a more realistic model than the Wiener process for the representation of Brownian motion: Xt represents the velocity of a particle undergoing Brownian motion.

According to [13.3], its autocovariance is written as (for θ ≠ 0):

13.4. Notions on statistics for diffusion processes

We will simply give some indications on the estimation of the parameters of unilateral Ornstein–Uhlenbeck processes defined by:

If one can observe (Xt, 0 ≤ t ≤ T), one may construct a “perfect” estimator of σ2 by setting:

Indeed, we have a.s.1. We may therefore suppose σ2 to be known, and, without loss of generality, set σ2 = 1.

To estimate θ, the maximum likelihood method is used: X = (Xt, 0 ≤ t ≤ T) and W = (Wt, 0 ≤ t ≤ T) define random variables with values in the space C[0, T] of continuous functions defined on [0, T] equipped with the uniform norm. We may then show that PX has a density with respect to PW, and that the likelihood is written as:

where

whence the maximum likelihood estimator

A simpler empirical estimator is written as:

When T → +∞, these two estimators converge almost surely and are asymptotically Gaussian, thus:

If only Xδ, X2δ,…, nδ are observed, it may be noted that the process (Xtδ, ) is an AR(1) (see Chapter 14), and a maximum likelihood estimator may be determined for θ.

For a complete study of the theory of diffusion statistics, we refer to [KUT 04].

13.5. Exercises

EXERCISE 13.1.– Show the formula for integration by parts indicated in section 13.1.

EXERCISE 13.2.– Show that the Itô integral:

is a martingale.

EXERCISE 13.3.–

1) Let Xt = sinh(Wt + t). Show that:

2) Determine the solutions to this equation with the initial condition X0 = 0.

EXERCISE 13.4.– We are interested in solving the stochastic differential equation:

where the functions a(·) and b(·) are deterministic.

1) Give some conditions on these functions to assure the existence and uniqueness of the solutions. In the following, suppose these conditions are to be satisfied.

2) Calculate the solution A(t) of

3) Let ϕ(x, t) be a C2 function. Calculate dϕ(Z(t), t), and deduce the differential equation satisfied by Y(t) = Z(t)/A(t). From this, deduce Z(t). How would you solve

where m is deterministic?

4) Suppose a(t) = a < 0, b(t) = 1. Show that there exists one unique stationary solution, and give the covariance function of this solution.

EXERCISE 13.5.– Let X = (Xt, t ≥ 0) be a process that satisfies the stochastic differential equation:

where a and b are constant and W is a standard Wiener process. Suppose that .

1) Setting , t ≥ 0, use the Itô formula to show that (Yt, t ≥ 0) satisfies a stochastic differential equation (E1).

2) Setting , t ≥ 0, use (E1) to show that satisfies an ordinary differential equation (E2).

3) Solve (E2).

4) Study the asymptotic behavior of φ(t), when t tends to infinity, in function of (a, b).

5) Supposing that φ is constant, propose an estimator of (a, b) based on the observation of (Xt, 0 ≤ t ≤ T).

EXERCISE 13.6.– Let Y = (Yt,t ≥ 0) be a process that satisfies the stochastic differential equation:

with θ > 0, σ > 0, Y0 = 1, and W is a standard Wiener process.

1) Setting Zt = l/Yt, t ≥ 0, write a stochastic differential equation to which (Zt, t ≥ 0) is the solution.

2) Setting , express in the form of a stochastic integral.

3)Showthat (, t ≥ 0) is a Gaussian process and determine the distribution of the random variable , t ≥ 0.

4) Deduce the distribution of the random variable Yt, t ≥ 0.

EXERCISE 13.7.– For all λ ∈ [−π, π], let B(λ) be a centered Gaussian process satisfying Cov(B(s), B(t)) = (27π)−1(min(s, t) + π).

1) Define a stochastic integral with respect to B.

2) Show that B has independent increments.

3) Denote the stochastic integral with respect to the process B by I. If f is a step function, what is E(I2 (f))?

4) Deduce E(I(f)I(g)) for every function f and g of L2 (λ), where λ is the Lebesgue measure on [−π, π].

5) For all , let . We define the process by:

Show that this process is weakly stationary, and give its spectral density.

6) Determine the distribution of the process . Is this process strictly stationary?

---

1 This result was proved for θ = 0 in Chapter 12.