Chapter 2

Principles of Decision Theory

2.1. Generalities

The examples given in Chapter 1 show that a statistical problem may be characterized by the following elements:

– a probability distribution that is not entirely known;

– observations;

– a decision to be made.

Formalization: Wald’s decision theory provided a common framework for statistics problems. We take:

1) A triplet where P is a family of probabilities on the measurable space is called a statistical model. We often set P = {Pθ, θ ∈ Θ} where we suppose that is injective, and Θ is called the parameter space.

2) A measurable space is called a decision (or action) space.

3) A set of measurable mappings is called a set of decision functions (d.f.) (or decision rules).

Description: From an observation that follows an unknown distribution P ∈ P, a statistician chooses an element a ∈ D using an element d from .

Preference relation: To guide his/her choice, the statistician takes a preorder (i.e. a binary relation that is reflexive and transitive) on . One such preorder is called a preference relation. We will write it as so that reads “d1 is preferable to d2”. We say that d1 is strictly preferable to d2 if and .

The statistician is therefore concerned with the choice of a “good” decision as defined by the preference relation considered.

Risk function: One convenient way of defining a preference relation on is the following:

1) Θ being provided with a σ-algebra , we take a measurable map L from to called a loss function.

2) We set:

where R is called the risk function associated with L; it is often written in the following form:

where X denotes a random variable with distribution Pθ1 and Eθ the expected value associated with Pθ. We note that R takes values in .

3) We say that d1 is preferable to d2 if:

[2.1]

We will say that d1 is strictly preferable to d2 if [2.1] holds, and if there exists θ ∈ Θ such that:

INTERPRETATION 2.1.– L(θ, a) represents the loss incurred by the decision a when the probability of X is Pθ (or when the parameter is equal to θ). R(θ, d) then represents the average loss associated with the decision function d. The best possible choice in light of the preference relation defined by [2.1] becomes the decision that minimizes the average loss, whatever the value of the parameter.

EXAMPLE 2.1.–

1) In the example of quality control (chapter 1), the decision space contains two elements: a1 (accept the batch) and a2 (reject the batch). A decision rule is therefore a map from {1, …, r} to {a1, a2}.

The choice of a loss function may be carried out by posing:

where c1 and c2 are two given positive numbers.

2) In the measurement errors example, , and a decision function is a numerical measurable function defined on .

A common loss function is defined by the formula:

from which we have the quadratic risk function:

COMMENT 2.1.– In example 2.1(1), among others, we may very well envisage other sets of decisions. For example:

1) D′ = {a1, a2, a3} where a3 is the decision consisting of drawing a certain number of additional objects. The associated decision rules are called sequential.

2) D″ = {a1, a2, μ} where μ is a probability on {a1, a2}. In real terms, the decision “ μ ” consists of a random draw after μ. This non-deterministic (or randomized) method may seem surprising, but it is often reasonable, as we will see later.

A detailed study of the sequential and non-deterministic methods is beyond the scope of this book. In what follows, we will only treat certain particular cases.

2.2. The problem of choosing a decision function

DEFINITION 2.1.– A decision function is described as optimal in if it is preferable to every other element of .

If is too large or if the preference relation is too narrow, there is generally no optimal decision function, as the following lemma shows:

LEMMA 2.1.– If:

1) P contains two non-orthogonal2 probabilities P_θ1 and P_θ2,

2) D = Θ,

3) contains constant functions and is defined using the loss function L such that:

then there is no optimal decision rule in .

PROOF.– Let us consider the decision rules:

which obey

An optimal rule d will therefore have to verify the relations:

hence

therefore

which is a contradiction, since P_θ1 and P_θ2 are not orthogonal.

EXAMPLE 2.2.– This result is applied to example 2.1 (2).

1) To reduce , we may demand that it possesses properties of regularity for the envisaged decision functions. Among these properties, two are frequently used:

DEFINITION 2.2.– A decision function d is called unbiased with respect to the loss function L if:

EXAMPLE 2.3.– In example 2.2 is an unbiased decision rule.

   If a decision problem is invariant or symmetric with respect to certain operations, we may demand that the same is true for the decision functions.

   We will study some examples later.

2) We may, on the other hand, seek to replace optimality with a less strict condition:

   i) by limiting ourselves to the search for admissible decision functions (a d.f. is said to be admissible if no d.f. may be strictly preferred to it);

   ii) by substituting with a less narrow preference relation for which an optimal d.f. exists.

Bayesian methods, which we study in the following section, include these two principles.

2.3. Principles of Bayesian statistics

2.3.1. Generalities

The idea is as follows: we suppose that Θ is provided with a σ-algebra and we take a probability τ (called an“a priori probability” on ).

R being a risk function such that is measurable for every measurable mapping , we set:

where r is called the Bayesian risk function associated with R; it leads to the following preference relation:

An optimal d.f. for is said to be Bayesian with respect to τ.

DISCUSSION.– Bayesian methods are often criticized, as the choice of τ is fairly arbitrary. However, Bayesian decision functions possess a certain number of interesting properties; in particular, they are admissible, whereas this is not always the case for an unbiased d.f.

2.3.2. Determination of Bayesian decision functions

We suppose that Pθ has a density f (·, θ) with respect to some σ-finite measure λ on . Furthermore, f (·, ·) is assumed to be -measurable.

Under these conditions,

where t(·, θ) is defined Pθ almost everywhere by the formula:

A d.f. that minimizes ∫ L(θ, d(x))t(x, θ)dτ(θ) is therefore Bayesian. This quantity is called the a posteriori risk (x being observed).

INTERPRETATION 2.2.– If we consider the pair (X, θ) as a random variable with distribution f (x, θ)dλ(x)dτ(θ), t(x, ·) is then the conditional density of θ, given X = x. The a posteriori risk is interpreted as the expectation of L(θ, d(X)), given that X = x.

In the important case of and L(θ, a) = (θ − a)2, the d.f. that minimizes the a posteriori risk is the conditional expectation3 of θ with respect to X. This d.f. is therefore given by the formula:

In a certain sense, using the Bayesian method is equivalent to transforming the problem of the estimation of θ into a filtering problem: we seek to estimate the unobserved random variable θ from the observed random variable X.

EXAMPLE 2.4.–

1) . With respect to the Lebesgue measure on has the density

with

and

hence the marginal density of X

therefore

that is the distribution of θ given that X = x is .

We deduce Bayes’ rule

2) E = Θ = D =]0, 1[, Pθ = uniform distribution on ]0, θ[, λ = τ = uniform distribution on ]0, 1[. (X, θ) therefore has the density , hence and

COMMENT 2.2.– The fact that τ is a uniform distribution on ]0, 1[ does not mean that we have a priori no opinion on θ. In effect, such a choice implies, for example, that θ2 follows the density distribution ; this shows that we are not without opinion on θ2, and therefore on θ.

2.3.3. Admissibility of Bayes’ rules

THEOREM 2.1.–

1) If d0 is, a.s. for all θ, the only Bayes rule associated with τ, then d0 is admissible for R.

2) If , R(θ, d) is continuous on θ for all , τ supports all open , and r(τ, d0) < ∞ (where d0 is a Bayes rule associated with τ), then d0 is admissible for R.

PROOF.–

1) Let d be a d.f. preferable to d0, we then have:

and, since d0 is Bayesian, we have:

The uniqueness of d0 then implies that:

From this, we deduce:

therefore, d is not strictly preferable to d0.

2) If d0 was not admissible, there would exist such that:

By continuity, we deduce that there would exist an open neighborhood U of θ0 and a number ε > 0 such that:

Under these conditions:

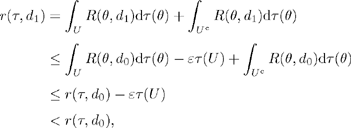
which is a contradiction, since d0 is Bayesian.

2.4. Complete classes

DEFINITION 2.3.– A class of decision functions is said to be complete (or essentially complete) if for all there exists that is strictly preferable (or preferable, respectively) to d.

The solution to a decision problem must therefore be sought in a complete class, or at least an essentially complete class.

DEFINITION 2.4.– Let μ be a measure on . A decision function d0 is said to be a generalized Bayesian decision function with respect to μ if:

EXAMPLE 2.5.– In example 2.4(1) in the previous section, is a generalized Bayesian decision function with respect to the Lebesgue measure.

We note that ; we say that is a Bayes limit. Under fairly general conditions relative to L, we may show that the Bayes limit decision functions are generalized Bayesian functions with respect to a certain measure μ (see, for example, [SAC 63]).

We now state a general Wald theorem, whose demonstration appears in [WAL 50]:

THEOREM 2.2.– If and if:

1) ;

2) :

3) :

then

2.5. Criticism of decision theory – the asymptotic point of view

As we have seen, decision theory provides a fairly convenient framework for the description of statistics problems. We may, however, make several criticisms of it.

First of all, this framework is often too general for the results of the theory to be directly usable in a precise, particular case. This is true for testing problems.

On the other hand, we may only obtain sufficient information on a decision to be made if we make use of a large number of observations of the studied random phenomenon. It is therefore interesting to pose a statistics problem in the following way: with the number of observations made, n, we associate a d.f. dn and study the asymptotic behavior of the sequence (dn) when n tends to infinity – particularly its convergence toward the “true” decision, and the speed of its convergence. This “asymptotic theory” is rich in results and applications.

For a more in-depth study of decision theory and Bayesian methods, we refer to [LEH 98] and [FOU 02].

2.6. Exercises

EXERCISE 2.1.– Let X be a random variable that follows the Bernoulli distribution where 0 ≤ θ ≤ 1. To estimate θ in light of X, we chose a priori a density distribution .

1) Determine the Bayes estimator of θ.

2) For k = 0, calculate the quadratic error of this estimator, and compare it to that of the estimator when θ varies from 0 to 1.

EXERCISE 2.2.– Let X be a random variable that follows a uniform distribution on ]0, θ[ (θ > 0). To construct a Bayesian estimator, we choose a priori the density distribution and choose the quadratic error as a risk function.

1) Determine the conditional density of θ knowing X. From this, deduce the Bayesian estimator of X.

2) Calculate the quadratic error of this estimator and compare it to the quadratic errors of X and the unbiased estimator 2X. Comment on the result.

EXERCISE 2.3.– Taking the previous exercise, and choosing as a risk function the error L1:

1) Preliminary question: let Z be a random variable whose distribution function F is continuous and strictly increasing on the support4 of PZ. Show that reaches its maximum for F(μ0) = 1/2 (μ0 is therefore the median of Z).

2) Determine the Bayesian estimator of X.

EXERCISE 2.4.– Let be a statistical model. We suppose that D = Θ and that the preference relation on is defined by the risk function R. Then let d0 be a Bayesian decision function such that R(θ, d0) is constant when θ varies in Θ.

Show that:

[2.2]

(A d.f. obeying [2.2] is called minimax: it minimizes the maximum risk on Θ.)

EXERCISE 2.5.– Let μ be a σ-finite measure on such that:

We consider the real random variable X whose density with respect to μ is written as:

and we seek to estimate g(θ) = −β′(θ)/β(θ).

1) Show that Eθ(X) = g(θ) and that Vθ(X) = g′(θ). Deduce from this that g is strictly monotone.

2) We put a priori the distribution onto . The risk function being the quadratic error, determine the Bayesian estimator of g(θ) associated with τσ, i.e. .

3) Show that:

4) From this, deduce that is an admissible estimator.

EXERCISE 2.6.– Let X1, …, Xn be a sample of the Bernoulli distribution , θ ∈]0, 1[. It is proposed that a minimax estimator T of θ be constructed for the quadratic error. In other words, T minimizes

1) We set . Calculate .

2) Considering the estimator:

calculate M(T) and compare it to .

3) Show that T is a Bayesian estimator with respect to the a priori density distribution:

We give the formula:

4) Establish the following result: “A Bayesian estimator whose quadratic risk does not depend on θ is minimax”. Thus, deduce that T is minimax.

EXERCISE 2.7.– We suppose that X follows a Poisson distribution with parameter θ, θ ∈]0, +∞[= Θ = D and that L(θ, θ′) = (θ − θ′)2.

We want to define a Bayesian estimator of θ. For this, we take as an a priori distribution the Gamma distribution Γ(α, β) with density:

Show that the conditional distribution of θ, given that X = x, is the Gamma distribution Γ(α + x, β/β + 1). From this, deduce that the Bayesian estimator of θ is defined by:

---

1 To avoid the introduction of an additional space, we may assume that X is the identity of E. This will henceforth be the case, unless otherwise indicated.

2 P_θ1 and P_θ2 are orthogonal if there exists N1 and N2 disjoint such that P_θi (N_i) = 1; i = 1, 2.

3 see Chapter 3, page 21.

4 The support of Pz is the smallest closed S such that Pz(S) = 1.