Chapter 7

Asymptotic Statistics

7.1. Generalities

Asymptotic statistics is the study of decision rules when the number of observations tends to infinity.

Theoretically, the asymptotic model may be described as follows: one considers a statistical model written as , a sequence of sub-σ-algebras of , and a sequence (dn, n ≥ 1) of -adapted decision rules (i.e. dn is -measurable for all n ≥ 1).

The decision space being provided with a distance δ, we say that (dn) is convergent in probability if:

where aθ denotes the “correct” decision when the value of the parameter is θ.

In the usual case, where (Xn,n ≥ 1) is a sample from Pθ, θ ∈ Θ, we have , , and , and the convergence in probability may be rewritten as:

In the rest of this chapter, we will limit ourselves to the case of a sample.

EXAMPLE 7.1.–

1) An estimator (Tn) of is convergent in probability if:

2) A test (φn) of Θ0 against Θ1 is convergent in probability if:

In effect, convergence in probability and convergence in mean are equivalent for uniformly bounded random variables.

REMARK 7.1.–

1) We define almost sure convergence, convergence in quadratic mean, etc., in a similar way.

2) In the case of a test, it is often more interesting to consider the convergence defined by:

[7.1]

and Eθ(φn) → 1, θ ∈ Θ1, since this corresponds to the convergence of the size and the power of the test. However, in the usual cases, [7.1] is often replaced with the weaker condition αn → α where α is given1.

– Existence of a convergent sequence of decision rules

The problem of the existence of such a sequence is quite challenging, and lies outside the scope of this book. We simply make two remarks on this subject:

1) In the case of a real sample, since is almost surely convergent in distribution toward the true distribution μ (the Glivenko–Cantelli theorem), if the real parameter φ(μ) is the limit of a sequence (φk(μ),k ≥ 1) where the φk are continuous for convergence in distribution, and if φk(μn) is defined for k ≥ 1 and n ≥ 1, then converges almost surely to μ for (kn) well-chosen.

Under very general hypotheses, we may show that the condition φ = lim φk is necessary and sufficient for the existence of a convergent estimator of φ.

2) If and if (dn) converges almost surely, then Pθ,∞ is orthogonal to Pθ′,∞. In effect

and

and we have .

From this remark, we may derive existence conditions for convergent decision rules based on the “asymptotic separation” of and .

7.2. Consistency of the maximum likelihood estimator

Let us consider the asymptotic model and set

We make the following hypotheses:

1) Θ is an open set in ;

2) is injective and fθ · μ is not degenerate;

3) f(x, ·) is strictly positive and differentiable for all ;

4) ∂/∂θ log Ln (x(n), θ) = 0 has one unique solution, written as:

5) ∀θ1, θ2 ∈ Θ, log f(·, θ1) is -integrable.

Then:

THEOREM 7.1.– (Tn) converges almost surely to θ, θ ∈ Θ.

PROOF.– Let θ0 be the true value of the parameter. We have:

Applying Jensen’s inequality, we find:

(The inequality is strict, as the logarithm is strictly concave and the measures are not degenerate.)

Let us now set:

and

(since Θ is open, θ0 ± 1/m ∈ M for large enough m).

Then:

and ∀(x) ∈ Nc, ∀θ ∈ M (denumerable):

We now take ε > 0 and θ′,θ″ ∈ M such that:

For large enough n, we will have Un (x(n), θ8242;) < 0 and Un(x(n), θ″) < 0, yet Un(x(n),θ0) = 0; therefore, the unique maximum of Un (i.e. Tn) belongs to ]θ′, θ″[.

CONCLUSION.– On Nc, Tn → θ0.

7.3. The limiting distribution of the maximum likelihood estimator

THEOREM 7.2.– Under the previous hypotheses (section 7.2, Hypotheses (1)–(5)), and the following hypotheses:

6) ∂2f/∂θ2 exists and is uniformly continuous in θ, with respect to x;

7) the equality ∫ f (x, θ)dμ(x) = 1 is twice differentiable under the integral sign;

8) the information quantity nI(θ) ∈] 0, +∞ [,

we have:

COMMENT 7.1.– We may interpret this result in the following way: the “asymptotic variance” of Tn is [nI(θ)]−1 therefore Tn is “asymptotically efficient”.

PROOF.– Let us set:

The likelihood equation is written as ϕn = 0. Moreover

[7.2]

where belongs to the interval with endpoints θ0 and Tn. We deduce that (Theorem 7.1).

Now

where

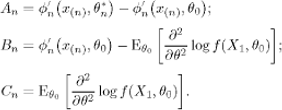
We will study these three terms separately.

1)

hence

Hypothesis (6) and therefore leads to .

2) from the strong law of large numbers.

3) Following from Hypothesis (7), C = −I(θ0), but [7.2] implies that:

Thus, (the central limit theorem) and from the above , from which we deduce (left as an exercise)

7.4. The likelihood ratio test

Given the problem of testing θ ∈ Θ0 against θ ∈ Θ1, where the model is assumed to be dominated and of liklihood L(X, θ), we set:

The principle of a test based on Λ is as follows: under the assumption of regularity

where is the maximum likelihood estimator of θ. When θ ∈ Θ0, Λ is in the neighborhood of 1, and we are therefore led to consider the test with critical region Λ < λ. This test is called the likelihood ratio test. When Θ0 = {θ0}, this is called a λ test, as envisaged in Chapter 6.

The asymptotic behavior of Λ is given by the following theorem.

THEOREM 7.3.– Under the hypotheses of Theorem 7.2, if Θ0 = {θ0} and if the true distribution is , then we have:

PROOF.– For simplicity, we set:

where denotes the maximum likelihood estimator. Then:

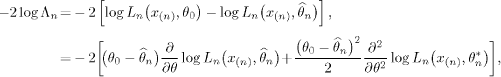
where is in the interval with endpoints and θ0.

Yet since , we have, with the notation from Theorem 7.2:

but we have seen that

and that

from which we deduce the result.

COROLLARY 7.1.– Under the previous hypotheses, for the problem of testing θ = θ0 against θ ∈ Θ−{θ0},the test Λn < λn, where λn is determined by where α ∈ ]0,1[, is convergent with asymptotic size α. Moreover, −2 log λn → k, where k is determined by P (χ2(1) > k) = α.

PROOF.–

1) For all ε > 0,

therefore, for large enough n, k − ε < −2 log Λn < k + ε.

Consequently, −2 log Λn → k.

2) We show that Pθ,∞(Λn < λn) → 1 for θ ≠ θ0. First, from the strong law of large numbers:

Since and since −2 log λn→ k, we deduce that:

Then, since for θ ≠ θ0,

where

we finally have:

COMMENT 7.2.– Other asymptotic results are demonstrated in Chapter 8, which is dedicated to non-parametric methods.

7.5. Exercises

EXERCISE 7.1.– Let X1, …, Xn be a sample of the Pareto distribution with density , where α is assumed to be known and r to be unknown. Determine the maximum likelihood estimator of r and show that it converges almost surely.

EXERCISE 7.2.– Let X1, …, Xn be a sample of a distribution on whose distribution function is continuous and strictly increasing. Define, in a precise manner, the empirical median and show that it converges almost surely to the theoretical median.

EXERCISE 7.3.– Let be a sequence of independent and identically distributed variables of a distribution with density θ exp(−θx), x ≥ 0. X1, …,Xn being observed, we estimate θ by setting .

1) Calculate EX1. Prove the almost sure convergence in probability of to θ. Give the limiting distribution of .

2) Give the distribution of and, from it, deduce that of . Calculate , , and .

3) We now consider the estimator . Calculate , , and . Which estimator do you prefer?

EXERCISE 7.4.– Let (X1, Y1),…, (Xn, Yn) be a sample of the two-dimensional normal distribution of zero mean and covariance matrix:

where ρ is an unknown parameter such that |ρ| < 1. We recall that the density of (X1, Y1) is written as:

1) We estimate ρ using

Calculate ET1 and Var(T1); show that T1 converges almost surely and determine its limiting distribution. Find a confidence region for ρ.

2) Directly determine the expected value and the variance of X1 − Y1. Deduce its distribution. Find a convergent estimator of ρ, i.e. T2, based on the statistic . Indicate how we may calculate its asymptotic variance.

3) Write the likelihood equation and show that it almost surely has a unique solution for large enough n. How can we calculate the asymptotic variance of the maximum likelihood estimator T3? Carry out the calculation.

4) Compare the asymptotic variances of T1, T2 and T3. Conclude from the result.

EXERCISE 7.5.– Let X1,…, Xn be a sample of . We wish to study the convergence of the estimator of θ defined by:

1) Establish the following preliminary result: “Let P be a probability, and let (An) and (Bn) be two sequences of events such that P(An) → α ∈ [0,1] and P(Bn) → 1; then P(An ∩ Bn) → α”.

2) Show that, when n→∞,

3) Show that Tn converges in probability to θ for all .

4) Determine the asymptotic variance of Tn when θ = 0 and compare it to that of . Conclude.

EXERCISE 7.6.– Let Xi, i = 1,…, n, be independent and identically distributed with density:

where k is known, k ∈ [1, 2]. This density is that of a variable which is obtained by a homothetic transformation with ratio 2, and a translation of θ − 1 of a variable with a beta distribution β(k, k)2.

1) We seek to characterize the maximum likelihood estimator , for k ≠ 1.

   i) Show that, if exists, then . Verify that this interval is non-empty (Pθ-almost sure ∀θ).

   ii) Show that, for θ ∈ [X(n) − 1,X(1) + 1], the derivative of the log-likelihood is written in two ways:

   Prove that and that is strictly decreasing on this interval.

   iii) Deduce that the maximum likelihood estimator is the unique solution to . Show that the solution of requires to determine the roots of a polynomial of high degree. What will happen for k = 1?

2) We now study the asymptotic properties of .

   i) Is the model exponential? (Distinguish between the two cases k = 1 and k ∈ ]1, 2].)

   ii) For k ≠ 1, show that we may find a constant C (which does not depend on θ) such that, for sufficiently small x, we have:

   Deduce that:

   iii) Show that, for all y > 0 and for sufficiently large n,

and determine the limit of the right-hand side. Deduce that, except eventually for tends in probability toward 0. What convergence rate may we expect for the maximum likelihood estimator?

---

1 We then say that (φn) is a convergent test of asymptotic size α.

2 A beta distribution has the density .