CHAPTER 5
INFERENCE OF VOHRADSKÝ’S MODELS OF GENETIC NETWORKS USING A REAL-CODED GENETIC ALGORITHM
Shuhei Kimura
Graduate School of Engineering, Tottori University, Tottori, Japan
5.1 INTRODUCTION
Proteins play major roles in cells, and are synthesized using information from genes. Gene expression is a process by which information from a gene is used in the synthesis of a protein. The analysis of gene expression is regarded as an important means to understand biological systems.
Advancements in biological technologies, such as deoxyribonucleic acid (DNA) microarrays and ribonucleic acid sequencing (RNA-seq), allow us to measure the expression levels of thousands of genes. However, in order to utilize these technologies, we must find a way to extract hidden information from the measured gene expression data. The inference of genetic networks is considered a promising approach for extracting useful information from these data. A genetic network, which is also referred to as a gene regulatory network, is a functioning circuit in living cells. The inference of genetic networks is a problem in which mutual interactions among genes are deduced from time series of gene expression data. The inferred model of the genetic network is conceived of as a tool to help biologists generate hypotheses and facilitate the design of their experiments. A number of researchers have taken an interest in the inference of genetic networks, and, therefore, a number of genetic network inference methods have been proposed [2, 4, 8, 10, 11, 12, 23, 21, 25, 36, 37, 44, 45].
The inference of genetic networks is often defined as nonlinear function optimization problems. In order to infer reasonable genetic networks, therefore, some inference methods use evolutionary algorithms as a function optimizer (e.g., Refs. [6, 16, 18, 20, 24, 27, 28, 34, 35, 42, 43]). The dimensions of the objective functions defined in these methods generally depend on the number of genes contained in a target genetic network. Therefore, when trying to analyze a genetic network consisting of a large number of genes, high-dimensional nonlinear function optimization problems must be solved. Among these inference methods, this chapter describes a method proposed by Kimura et al. that resolves this high dimensionality by defining the inference of a genetic network as several two-dimensional function optimization problems [22].
5.2 MODEL
Numerous models have been used to describe genetic networks, each of which has its own merits and demerits [13, 15, 17, 39, 44]. Our group has focused on models based on sets of differential equations, since they have an ability to capture the dynamic behavior of gene expression. When we use a set of differential equations, a genetic network is described as
where Xn is the expression level of the nth gene, N is the number of genes contained in the target network, and Fn is a function of arbitrary form. The purpose of a genetic network inference problem based on a set of differential equations is to identify the function Fn from the observed gene expression levels.
In order to identify the function Fn, Sakamoto and Iba [31] have proposed to use a genetic programming, a kind of evolutionary algorithm. The scope of their method has been limited, however, as the difficulty of identifying arbitrary functions restricts application to small-scale genetic network inference problems. It is generally better to approximate the function Fn than to try to identify it. In many earlier studies, the function Fn was approximated using a set of differential equations of a fixed form. When we use a set of differential equations of a fixed form to describe genetic networks, the purpose of the genetic network inference problem is to estimate all of the parameters contained in the model. A linear model is a well-studied model based on a set of differential equations of a fixed form, and several inference methods based on the linear model have been proposed [14, 44]. The computation times of these methods are reportedly very short. As the linear model requires that the system is operating near a steady state, however, it is unsuitable for analyzing the time series of gene expression levels [44]. An S-system model is another well-studied model based on a set of differential equations of a fixed form [39]. This model has a rich structure capable of capturing various dynamics and can be analyzed by several available methods. A number of inference methods based on the S-system model have thus been proposed [5, 6, 18, 20, 19, 24, 27, 35, 40]. However, there are a large number of parameters in the S-system model. For example, the number of parameters in the linear model is N(N + 1), where N is the number of genes contained in the target network. On the other hand, the number of parameters in the S-system model is 2N(N + 1). Therefore, we must give the inference methods based on the S-system model more gene expression data to obtain reasonable results.
When trying to infer genetic networks, we should use a model that has an ability to approximate actual biochemical reactions. Moreover, as it is generally difficult to measure a sufficient amount of gene expression data, the model should contain fewer parameters. A model proposed by Vohradský seems to satisfy the requirements above, since the number of parameters is comparable to that of the linear model and it is reportedly capable of capturing the process of gene expression [38]. Because of its preferable features, several inference methods based on this model have been proposed [28, 42, 43], and the inference method described in this chapter [22] is also based on this model. The Vohradský’s model is a set of nonlinear differential equations of the form
where
and αn (> 0), βn (> 0), bn and wn = (wn, 1, wn, 2, …, wn, N) (n = 1, 2, …, N) are model parameters. The first and the second terms on the right-hand side of Equation (5.2) represent processes that contribute to the increase and decrease, respectively, in Xn. When the mth gene positively or negatively regulates the nth gene, the value for the parameter wn, m is positive or negative, respectively. On the other hand, when the nth gene is not regulated by the mth gene, the value for wn, m is 0.
In the inference of a Vohradský’s model of a genetic network, the purpose is to estimate all of the model parameters that produce time-series data consistent with the observed gene expression levels. The numbers of the parameters αn, βn, bn, and wn, m (n, m = 1, 2, …, N) are N, N, N, and N2, respectively. The total number of model parameters to be estimated is therefore N(N + 3).
5.3 INFERENCE BASED ON BACK-PROPAGATION THROUGH TIME
The Vohradský’s model can be viewed as a recurrent neural network. Therefore, in order to estimate the parameters of this model, we can use learning algorithms for recurrent neural networks, such as a back-propagation through time (BPTT) [41]. When we use the BPTT, the inference of a Vohradský’s model of a genetic network consisting of N genes is defined as a minimization problem of the following function:
where α = (α1, α2, …, αN), β = (β1, β2, …, βN), b = (b1, b2, …, bN), and w = (w1, 1, w1, 2, …, wN, N) are the model parameters, and K is the number of measurements. ![]() and
and ![]() are the measured and the computed expression levels of the nth gene at time tk, respectively. However,
are the measured and the computed expression levels of the nth gene at time tk, respectively. However, ![]() is not computed from a set of differential equations (5.2), but from its discrete form, that is,
is not computed from a set of differential equations (5.2), but from its discrete form, that is,
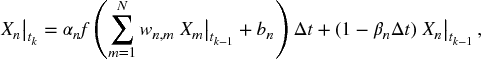
where Δt = tk − tk − 1.
The existing inference methods based on the Vohradský’s model have been designed according to this problem definition [28, 42, 43]. As the training of recurrent neural networks is not always easy, evolutionary algorithms are used as function optimizers. The method proposed by Xu et al. uses a hybrid of a differential evolution and a particle swarm optimization to optimize the objective function above [42]. Xu et al. [43] also proposed another inference method that uses two different particle swarm optimizations. This method uses one particle swarm optimization to infer the structure of the target genetic network and the other to estimate the parameters of a Vohradský’s model. It is known that a gene is regulated by a small number of genes [33], and the inference method [43] was developed to introduce this knowledge into the genetic network inference. On the other hand, in order to optimize the objective function (5.3), Palafox and Iba [28] have used population-based incremental learning [3], a kind of estimation of distribution algorithm. Although their method has an ability to infer genetic networks with very short computation times, it is unable to estimate model parameters precisely.
In contrast to these inference methods, the method proposed by Kimura et al. estimates the model parameters by solving simultaneous equations, as described in Section 5.4 [22].
5.4 INFERENCE BY SOLVING SIMULTANEOUS EQUATIONS
As mentioned in Section 5.3, several genetic network inference methods based on the Vohradský’s model have been proposed [28, 42, 43]. As these methods are designed on the basis of a learning algorithm for recurrent neural networks, they estimate all of the model parameters simultaneously. The number of parameters in the Vohradský’s model is N(N + 3), where N is the number of genes contained in the network. When trying to analyze genetic networks with a large number of genes, high-dimensional nonlinear function optimization problems must be solved.
In order to overcome this high dimensionality, the inference method proposed by Kimura et al. [22] first divides the inference problem of a Vohradský’s model of a genetic network consisting of N genes into N subproblems, each of which corresponds to each gene. Our method then defines each subproblem as a two-dimensional function optimization problem. This section describes the nth subproblem corresponding to the nth gene.
5.4.1 Problem Definition
The nth subproblem is defined as the problem of solving the following simultaneous equations:
where ![]() is the expression level of the mth gene at time tk,
is the expression level of the mth gene at time tk, ![]() is the time derivative of the expression level of the nth gene at time tk, and K is the number of measurements. Note that
is the time derivative of the expression level of the nth gene at time tk, and K is the number of measurements. Note that ![]() is measured using some biological technology.
is measured using some biological technology. ![]() is, on the other hand, estimated directly from the observed time series of the gene expression levels using a smoothing technique, such as spline interpolation [29], local linear regression [9], and so on. By solving the simultaneous equations (5.5) in the nth subproblem, the method estimates the parameters corresponding to the nth gene, that is, αn, βn, bn, and wn = (wn, 1, wn, 2, …, wn, N). Based on a similar idea, several genetic network inference methods have been proposed [7, 19, 23, 40, 44].
is, on the other hand, estimated directly from the observed time series of the gene expression levels using a smoothing technique, such as spline interpolation [29], local linear regression [9], and so on. By solving the simultaneous equations (5.5) in the nth subproblem, the method estimates the parameters corresponding to the nth gene, that is, αn, βn, bn, and wn = (wn, 1, wn, 2, …, wn, N). Based on a similar idea, several genetic network inference methods have been proposed [7, 19, 23, 40, 44].
When we simply use a least-squares method to solve these simultaneous equations, for example, the estimation of the model parameters is defined as a minimization problem of the function
where

It is not always easy to solve this problem, however, since the objective function (5.6) is nonlinear. Moreover, as the dimension of this function is N + 3, the difficulty in optimizing it increases with an increase in the number of genes contained in the network, that is, N. In order to cope with this difficulty, our group proposed an efficient technique for solving the simultaneous equations (5.5), as mentioned in Section 5.4.2.
5.4.2 Efficient Technique for Solving Simultaneous Equations
5.4.2.1 Concept
To solve the simultaneous equations (5.5), our method uses a feature arising from the transformation of the equations, described below.
By rearranging the kth member of Equations (5.5), we have
where

By applying ![]() to Equation (5.7), we obtain
to Equation (5.7), we obtain

By taking logarithms of both sides of the above equation, we then have

All of the members of the simultaneous equations (5.5) can be converted in the same way. We therefore have new simultaneous equations:
Note that, although these transformed simultaneous equations are nonlinear with respect to the parameters αn and βn, they are linear with respect to the parameters bn and wn = (wn, 1, wn, 2, …, wn, N). This fact suggests that, when the parameters αn and βn are given, the other parameters bn and wn are easily estimated. Our method uses this feature for solving the simultaneous equations (5.5).
5.4.2.2 Objective Function
Our inference method uses a least-squares method to solve the simultaneous equations (5.5). As mentioned in Section 5.4.2.1, however, we can easily estimate the parameters bn and wn, when the parameters αn and βn are given. Therefore, in order to solve the simultaneous equations, our method searches for optimum values for the parameters αn and βn only. The objective function of this problem is thus defined as
where

and b*n and w*n = (wn, 1*, w*n, 2, …, wn, N*) are the optimal values for bn and wn = (wn, 1, wn, 2, …, wn, N), respectively, under given αn and βn. In Section 5.4.2.3, we will describe a method for obtaining b*n and w*n.
Note here that the shapes of the objective functions (5.6) and (5.11) are the same. The objective function (5.11) is therefore still nonlinear. Its low dimensionality however makes the problem much easier to solve.
5.4.2.3 Estimation of b*n and w*n
When trying to compute a value for the objective function (5.11), we must always provide values for b*n and w*n. In our approach, they serve as the solution of a set of the transformed equations (5.10) under given αn and βn. Note that, when the parameters αn and βn are given, these equations are linear with respect to the unknown parameters, that is, bn and wn. We can thus easily estimate b*n and w*n. In our approach, we define the estimation of these parameters as the following constrained function minimization problem:
subject to

where

ξ+k and ξ−k are slack variables, and γ+k, γ−k, δ and C are constant parameters. In the problem (5.12), we treat the parameters αn and βn as constants. Note that, whenever trying to compute a value for the objective function (5.11), we must always solve the function optimization problem (5.12) (see Figure 5.1).
ξ+k and ξ−k represent the differences between the left- and the right-hand sides of the kth member of the simultaneous equations (5.10). The first term of the objective function of the problem (5.12), that is, ![]() , is thus a weighted sum of the differences between the left- and right-hand sides of Equations (5.10). As described in Section 5.2, on the other hand, when the nth gene is not regulated by the mth gene, the parameter corresponding to this regulation, that is, wn, m, is 0 in the Vohradský’s model. Therefore, most wn, m values should be 0 because genetic networks are known to be sparsely connected [33]. The second term of the objective function, that is, ∑Nm = 1|wn, m|, introduces this knowledge into the parameter estimation.
, is thus a weighted sum of the differences between the left- and right-hand sides of Equations (5.10). As described in Section 5.2, on the other hand, when the nth gene is not regulated by the mth gene, the parameter corresponding to this regulation, that is, wn, m, is 0 in the Vohradský’s model. Therefore, most wn, m values should be 0 because genetic networks are known to be sparsely connected [33]. The second term of the objective function, that is, ∑Nm = 1|wn, m|, introduces this knowledge into the parameter estimation.

Figure 5.1 The computation of the objective function (5.11).
The transformation of the simultaneous equations (5.5), described in Section 5.4.2.1, can be done, only when the condition 0 < Yk < 1 is satisfied. Even when the optimum values are set for αn and βn, however, the noise contained in the observed gene expression data may mean that the condition above is not satisfied. Our approach thus introduces a threshold parameter δ, and sets its value to 10− 10. On the other hand, we should note that, when Yk approaches 0 or 1, the term ![]() contained in the kth member of the transformed simultaneous equations (5.10) approaches − ∞ or + ∞, respectively. Therefore, when Yk is approximately equal to 0 or 1, the transformation of the kth member of Equations (5.5) would amplify the noise contained in the measurement data. We should not rely too much on the equations transformed under these conditions. In order to introduce this notion into the parameter estimation, we set the constant parameters γ+k and γ−k to
contained in the kth member of the transformed simultaneous equations (5.10) approaches − ∞ or + ∞, respectively. Therefore, when Yk is approximately equal to 0 or 1, the transformation of the kth member of Equations (5.5) would amplify the noise contained in the measurement data. We should not rely too much on the equations transformed under these conditions. In order to introduce this notion into the parameter estimation, we set the constant parameters γ+k and γ−k to


The problem (5.12) can be converted into a linear programming problem. Therefore, we can always find an optimum solution to the problem. In order to solve this problem, our inference method uses an interior point method [26].
5.5 REXSTAR/JGG
Any function optimization algorithm can be used to minimize the objective function (5.11). The defined functions are expected to be easily optimized, since they are only two dimensional. When we applied a local search to the optimization problem of this function, however, we found several local optima. Therefore, in order to increase the probability of obtaining a reasonable solution, our inference method uses REX![]() /JGG [1] as a function optimizer. REX
/JGG [1] as a function optimizer. REX![]() /JGG, which is a real-coded genetic algorithm, a sort of evolutionary algorithm, reportedly shows excellent performance for many benchmark problems. REX
/JGG, which is a real-coded genetic algorithm, a sort of evolutionary algorithm, reportedly shows excellent performance for many benchmark problems. REX![]() /JGG uses just generation gap (JGG) as a generation alternation model and real-coded ensemble crossover
/JGG uses just generation gap (JGG) as a generation alternation model and real-coded ensemble crossover![]() (REX
(REX![]() ) as a recombination operator. This section describes each of the operators in detail.
) as a recombination operator. This section describes each of the operators in detail.
5.5.1 JGG
JGG is a generation alternation model developed chiefly for multiparental recombination operators. The generation alternation model is a procedure for selecting individuals to breed and for selecting individuals to form a new population in the next generation. The following is an algorithm of JGG.
[Algorithm: JGG]
Initialization
As an initial population, create np individuals. As REX
 /JGG is a real-coded genetic algorithm, these individuals are represented as s-dimensional real number vectors, where s is the dimension of the search space. Set Generation = 0.
/JGG is a real-coded genetic algorithm, these individuals are represented as s-dimensional real number vectors, where s is the dimension of the search space. Set Generation = 0.Selection for Reproduction
Randomly select m individuals without replacement from the population. The selected individuals, expressed here as p1, p2, …, pm, are used as the parents for the recombination operator in the next step. As mentioned in the following section, REX
 uses s + 1 parents, that is, m = s + 1.
uses s + 1 parents, that is, m = s + 1.Generation of Offsprings
Generate nc children by applying the recombination operator to the parents selected in the previous step. Our inference method uses REX
 as the recombination operator.
as the recombination operator.Selection for Survival
Select the best m individuals from the family containing the m parents, that is, p1, p2, …, pm, and their children. Then, replace the m parents with the selected individuals. In the original JGG, the best m individuals are selected only from the children. However, we slightly modified its algorithm as this optimization process seemed to be unstable.
Termination
Stop if the halting criteria are satisfied. Otherwise, Generation ← Generation + 1, and then return to step 2.
5.5.2 REX
REX![]() is a multiparental recombination operator. It uses s + 1 parents, where s is the dimension of the search space, and generates nc (> s + 1) children according to the following algorithm:
is a multiparental recombination operator. It uses s + 1 parents, where s is the dimension of the search space, and generates nc (> s + 1) children according to the following algorithm:
[Algorithm: REX![]() ]
]
- Generate reflection points
 of the parents p1, p2, …, ps + 1, that is,
(5.13)where
of the parents p1, p2, …, ps + 1, that is,
(5.13)where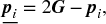

- Compute the objective values of the s + 1 reflection points generated in the previous step. In REX
 , these reflection points are treated as the children.
, these reflection points are treated as the children. - From the parents and their reflection points, select the best s + 1 individuals with respect to the objective value, and then compute the center of the gravity of the selected s + 1 individuals. This study represents this as Gb.
- Generate nc − s − 1 children by applying the following equation nc − s − 1 times. Note that the s + 1 reflection points generated in step 1 are treated as the children. The total number of the children generated by REX
 is therefore nc:
(5.14)where c represents the child, and
is therefore nc:
(5.14)where c represents the child, and ξtis and ξis are random numbers drawn from uniform distributions [0, t] and
ξtis and ξis are random numbers drawn from uniform distributions [0, t] and
 , respectively, where t is a hyper-parameter named a step-size parameter.
, respectively, where t is a hyper-parameter named a step-size parameter.

Figure 5.2 Generation of offspring by REX .
.
REX![]() estimates a global structure of a landscape of an objective function, disregarding its local roughness. The estimated global structure is used to generate offspring, that is, the region where children are generated is enlarged toward the gradient descent direction with respect to the estimated global structure (Figure 5.2). Because of this feature, REX
estimates a global structure of a landscape of an objective function, disregarding its local roughness. The estimated global structure is used to generate offspring, that is, the region where children are generated is enlarged toward the gradient descent direction with respect to the estimated global structure (Figure 5.2). Because of this feature, REX![]() /JGG has an ability to find optimum solutions with a smaller number of function evaluations.
/JGG has an ability to find optimum solutions with a smaller number of function evaluations.
In the original paper of REX![]() /JGG, the following settings are recommended for its hyper-parameters: the population size np is set between 2s and 20s; the number of children generated per selection nc is set between 2s and 3s; and the step-size parameter t is set between 2.5 and 15.
/JGG, the following settings are recommended for its hyper-parameters: the population size np is set between 2s and 20s; the number of children generated per selection nc is set between 2s and 3s; and the step-size parameter t is set between 2.5 and 15.
5.6 INFERENCE OF AN ARTIFICIAL NETWORK
In order to confirm that our method is capable of estimating reasonable values for the parameters of the Vohradský’s model, we applied it to an artificial genetic network inference problem.
5.6.1 Experimental Setup
We used a Vohradský’s model with four genes (N = 4) as a target network [43]. The model parameters and the network structure of this system are given in Table 5.1 and Figure 5.3, respectively. Note that, as this network consists of four genes, our inference method solves four individual two-dimensional function optimization problems to estimate all of the model parameters.
Table 5.1 The model parameters of the artificial network
| n | wn, 1 | wn, 2 | wn, 3 | wn, 4 | bn | αn | βn |
| 1 | 20.0 | −20.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.1 |
| 2 | 15.0 | −10.0 | 0.0 | 0.0 | −5.0 | 0.2 | 0.2 |
| 3 | 0.0 | −8.0 | 12.0 | 0.0 | 0.0 | 0.2 | 0.2 |
| 4 | 0.0 | 0.0 | 8.0 | −12.0 | 0.0 | 0.2 | 0.2 |
As the observed gene expression patterns, three sets of time-series data, each covering four genes, were computed from the differential equations (5.2) on the target model. The sets began from initial values randomly generated in [0.0, 1.0], and 50 sampling points for the time-series data were assigned to each gene in each set. The number of observations K is therefore 3 × 50 = 150. A sample of the time-series data we generated is shown in Figure 5.4. In a practical application, these sets would be obtained by actual biological experiments under different experimental conditions. This experiment simulated no measurement noise in the computed data. The time derivatives of the gene expression levels were thus directly computed from the model (5.2) of the target network. In this experiment, we estimated the parameters of the target model only from the gene expression levels and their derivatives.
We performed 10 trials, each with different sets of gene expression data. We considered the model parameters to be successfully estimated only when the value of the objective function (5.11) dropped to less than 1.0 × 10− 6. As the parameters αn and βn contained in the objective function (5.11) are both positive, this study searched for them in a logarithmic space. Their search area was set to [ − 3.0, 3.0]2. Based on the preliminary experiments, we set the constant parameter C contained in the constrained function minimization problem (5.12) to 2000. In accordance with the recommended values, this study used the following values for the hyper-parameters of REX![]() /JGG [1]: the population size np is 40; the number of children generated per selection nc is 6; and the step-size parameter t is 2.5. Each run of REX
/JGG [1]: the population size np is 40; the number of children generated per selection nc is 6; and the step-size parameter t is 2.5. Each run of REX![]() /JGG was continued until the maximum number of generation alternations reached 250.
/JGG was continued until the maximum number of generation alternations reached 250.

Figure 5.3 The structure of the artificial network.

Figure 5.4 A sample of time-series data used for inferring the artificial genetic network.
5.6.2 Results
The inference method described here succeeded in estimating the parameter values with precision in seven trials. In these trials, the parameters were estimated with high precision (Table 5.2). Even in the rest of the trials, most of the parameters were correctly estimated. Table 5.3 shows a sample of the model parameters estimated in one of the failed trials. As described previously, the inference method divided the parameter estimation problem of the target network here into four subproblems, each of which is defined as a two-dimensional function optimization problem. In this experiment, our method therefore solved 4 × 10 = 40 subproblems and failed to find the optimum solutions for only 3 of these 40 subproblems. While the averaged objective value (5.11) of the three failed subproblems was 1.590 × 10− 3 ± 2.120 × 10− 3, that of the other subproblems was 4.607 × 10− 9 ± 1.622 × 10− 8. When we gave the correct parameter values to the objective functions of the three failed subproblems, we obtained better objective values. The solutions found in the three failed subproblems are therefore local optima. To estimate all of the model parameters for this network, our method took about 10.4 ± 0.1 min on a single-CPU personal computer (Pentium IV 2.8 GHz).
Table 5.2 A typical sample of the parameters correctly estimated
| n | wn, 1 | wn, 2 | wn, 3 | wn, 4 | bn | αn | βn |
| 1 | 20.003 |
−20.002 |
0.000 |
−0.001 |
0.000 |
0.100 |
0.100 |
| 2 | 15.000 |
−10.000 |
0.000 |
0.000 |
−5.000 |
0.200 |
0.200 |
| 3 | −0.016 |
−7.991 |
11.986 |
−0.007 |
0.008 |
0.200 |
0.200 |
| 4 | 0.000 |
0.000 |
8.000 |
−12.000 |
0.000 |
0.200 |
0.200 |
Table 5.3 A sample of the parameters erroneously estimated
| n | wn, 1 | wn, 2 | wn, 3 | wn, 4 | bn | αn | βn |
| 1 | 1.405 |
−0.043 |
0.552 |
0.068 |
−2.424 |
4.004 |
1.561 |
| 2 | 15.000 |
−10.001 |
0.000 |
0.000 |
−5.000 |
0.200 |
0.200 |
| 3 | 0.000 |
−7.854 |
11.998 |
−0.275 |
0.031 |
0.200 |
0.200 |
| 4 | 0.000 |
0.000 |
8.000 |
−12.000 |
0.000 |
0.200 |
0.200 |
As described previously, the inference method proposed by Kimura et al. uses an evolutionary algorithm, REX![]() /JGG, to optimize the objective function (5.11). When we use a local search, instead of the evolutionary algorithm, we can shorten the computation time required for optimizing it. As the objective function seems to be multimodal, however, the use of the local search makes it difficult to infer reasonable genetic networks. When we used the modified Powell’s method [29], a local search algorithm, the computation time to estimate all of the model parameters was 3.4 ± 0.6 min on the personal computer (Pentium IV 2.8 GHz). The inference method with the modified Powell’s method, on the other hand, failed in finding the optimum solutions for 19 of the 40 subproblems. The averaged objective values (5.11) of the 19 failed subproblems and the other subproblems were 7.052 × 10− 2 ± 2.205 × 10− 1 and 1.653 × 10− 8 ± 7.392 × 10− 8, respectively. When we applied the inference method with the modified Powell’s method to artificial genetic network inference problems consisting of 30 genes, the method failed in finding reasonable solutions for 145 of 30 × 10 = 300 subproblems. This fact indicates that the difficulty in solving each subproblem defined in our approach is independent of the number of genes contained in the network. This is a preferable feature when we try to analyze larger-scale genetic networks.
/JGG, to optimize the objective function (5.11). When we use a local search, instead of the evolutionary algorithm, we can shorten the computation time required for optimizing it. As the objective function seems to be multimodal, however, the use of the local search makes it difficult to infer reasonable genetic networks. When we used the modified Powell’s method [29], a local search algorithm, the computation time to estimate all of the model parameters was 3.4 ± 0.6 min on the personal computer (Pentium IV 2.8 GHz). The inference method with the modified Powell’s method, on the other hand, failed in finding the optimum solutions for 19 of the 40 subproblems. The averaged objective values (5.11) of the 19 failed subproblems and the other subproblems were 7.052 × 10− 2 ± 2.205 × 10− 1 and 1.653 × 10− 8 ± 7.392 × 10− 8, respectively. When we applied the inference method with the modified Powell’s method to artificial genetic network inference problems consisting of 30 genes, the method failed in finding reasonable solutions for 145 of 30 × 10 = 300 subproblems. This fact indicates that the difficulty in solving each subproblem defined in our approach is independent of the number of genes contained in the network. This is a preferable feature when we try to analyze larger-scale genetic networks.
As mentioned in Section 5.3, several genetic network inference methods based on the Vohradský’s model have already been proposed [28, 42, 43]. However, for computational simplicity, they substantially limit the search space to αn = βn. In order to make a fair comparison, we therefore constructed an inference method based on the BPTT, referred to here as BPTTGA, that does not limit the search space. BPTTGA uses REX![]() /JGG to optimize the objective function (5.3). Although the computation time of BPTTGA was comparable to that of the proposed inference method, it was unable to estimate the model parameters precisely. When we used BPTTGA to infer the target network here, the averaged computation time on the personal computer (Pentium IV 2.8 GHz) and the averaged objective value were 9.3 ± 7.5 min and 5.987 × 10− 3 ± 1.062 × 10− 2, respectively. A typical sample of the model parameters estimated by BPTTGA is shown in Table 5.4. Note that, although the existing inference methods [28, 42, 43] substantially limit the search space, they were reportedly still unable to estimate the model parameters with precision.
/JGG to optimize the objective function (5.3). Although the computation time of BPTTGA was comparable to that of the proposed inference method, it was unable to estimate the model parameters precisely. When we used BPTTGA to infer the target network here, the averaged computation time on the personal computer (Pentium IV 2.8 GHz) and the averaged objective value were 9.3 ± 7.5 min and 5.987 × 10− 3 ± 1.062 × 10− 2, respectively. A typical sample of the model parameters estimated by BPTTGA is shown in Table 5.4. Note that, although the existing inference methods [28, 42, 43] substantially limit the search space, they were reportedly still unable to estimate the model parameters with precision.
Table 5.4 A sample of the parameters estimated by BPTTGA
| n | wn, 1 | wn, 2 | wn, 3 | wn, 4 | bn | αn | βn |
| 1 | 20.847 |
−21.373 |
−0.719 |
0.626 |
0.750 |
0.097 |
0.098 |
| 2 | 13.222 |
−8.787 |
0.092 |
−0.110 |
−4.421 |
0.194 |
0.189 |
| 3 | −0.821 |
−4.595 |
11.752 |
−4.166 |
1.093 |
0.189 |
0.189 |
| 4 | −0.023 |
0.024 |
6.553 |
−9.815 |
0.084 |
0.189 |
0.189 |
5.7 INFERENCE OF AN ACTUAL GENETIC NETWORK
We then used our inference method to analyze actual gene expression data.
5.7.1 Experimental Setup
We applied our inference method to the actual inference problem of the SOS DNA repair regulatory network in Escherichia coli (Figure 5.5) [32]. More than 30 genes, including lexA and recA, are known to be involved in this system. These genes are regulated by lexA and recA. In a basal state, LexA, a master repressor, is bound to the interaction site in the promoter regions of these genes. When DNA is damaged, RecA, another SOS protein, senses the damage and mediates LexA autocleavage. The decrease in LexA protein level halts the repression of the SOS genes, and they then start DNA repair. Once the damage has been repaired, RecA stops mediating LexA autocleavage, LexA accumulates and represses the SOS genes, and the cells return to their basal state.

Figure 5.5 The SOS DNA repair system in Escherichia coli.
This experiment analyzed the expression data of six genes, that is, uvrD, lexA, umuD, recA, uvrA, and polB, which had been measured by Ronen et al. [30] (N = 6). In order to infer the genetic network, therefore, we must solve six individual two-dimensional function optimization problems. These expression data have often been used to confirm the performances of inference methods [5, 6, 16, 23, 21, 19, 42, 43]. The original expression data contain four sets of time-series data. This experiment however used only two sets (the third and fourth sets), since these two had been measured under the same experimental conditions. Each set of time-series data consisted of 50 measurement values including the initial concentrations of 0. In the experiment, we removed the initial concentrations from both sets as models based on a set of differential equations cannot produce different time courses from the same initial conditions. The number of measurements K is thus 2 × 49 = 98. We normalized the data corresponding to each gene against its maximum expression level. The actual gene expression data are generally polluted by noise. This experiment therefore smoothed the normalized gene expression data using the local linear regression [9], a smoothing technique. We assigned a value of 10− 6 to expression levels with values of less than 10− 6, as the gene expression levels must not be negative. The time derivatives of the gene expression levels were estimated from the smoothed data. We performed 10 trials by changing a seed for pseudo-random numbers. All of the other experimental conditions were the same as those described previously.
5.7.2 Results
Although we performed 10 trials in this experiment, the inferred models had parameters similar to each other. A sample of the parameters of the inferred model is shown in Table 5.5. The computation time required for analyzing this system was approximately 13.9 ± 0.2 min on the personal computer (Pentium IV 2.8 GHz). We extracted the structures of the network from the estimated model parameters. The structures of the networks were extracted according to the following rules: when wn, m ⩾ Tn or wn, m ![]() −Tn, we conclude that the mth gene positively or negatively, respectively, regulates the nth gene, where Tn is a threshold; otherwise, we infer no regulation from the mth gene to the nth gene. This experiment set the threshold Tn to
−Tn, we conclude that the mth gene positively or negatively, respectively, regulates the nth gene, where Tn is a threshold; otherwise, we infer no regulation from the mth gene to the nth gene. This experiment set the threshold Tn to
Table 5.5 A sample of the estimated parameters in the analysis of the SOS DNA repair network in Escherichia coli
| n | wn, 1 | wn, 2 | wn, 3 | wn, 4 | wn, 5 | wn, 6 | bn | αn | βn |
| 1 | 4.412 |
−6.461 |
−0.355 |
0.000 |
5.901 |
−0.028 |
−4.185 |
0.337 |
0.055 |
| 2 | 6.054 |
−14.281 |
0.000 |
−7.562 |
19.762 |
1.667 |
−4.771 |
0.164 |
0.050 |
| 3 | 3.292 |
−11.752 |
7.891 |
−5.102 |
9.330 |
0.476 |
−4.997 |
0.604 |
0.095 |
| 4 | 4.177 |
−14.748 |
6.997 |
−3.644 |
11.519 |
0.000 |
−5.194 |
0.463 |
0.069 |
| 5 | 5.220 |
−20.101 |
9.979 |
−7.332 |
19.523 |
0.159 |
−4.301 |
0.265 |
0.252 |
| 6 | −0.372 |
−4.863 |
−17.110 |
10.927 |
15.720 |
7.347 |
−2.535 |
0.094 |
0.110 |
Genes 1, 2, 3, 4, 5, and 6 represent uvrD, lexA, umuD, recA, uvrA and polB, respectively.

Figure 5.6 The network structure extracted from the estimated parameters in the analysis of the SOS DNA repair network in Escherichia coli. Bold lines represent biologically plausible regulations.
All 10 of the inferred networks had the same structure. Figure 5.6 shows the structure of the network inferred by our inference method.
As mentioned before, LexA is known to repress the SOS genes. Therefore, the negative regulations of all of the genes by lexA, inferred by our method, are reasonable. Similarly, the negative regulation of lexA by recA would be reasonable, as RecA senses the damage of DNA and mediates LexA autocleavage. The regulation of umuD by recA, contained in the inferred network, also appears to be reasonable, since it is contained in a network now known [14]. As shown in the figure, the network inferred by our method still contains a number of regulations that are not mentioned above. Some of these regulations might be new findings. However, the rest should be false positives. In order to analyze larger-scale genetic networks using our inference method, therefore, we must find a way to reduce these erroneous results.
5.8 CONCLUSION
This chapter described the genetic network inference method proposed by Kimura et al. [22]. This method uses the Vohradský’s model to describe genetic networks. In order to infer a Vohradský’s model of a genetic network consisting of N genes, N(N + 3) model parameters must be estimated. The estimation of these parameters is generally defined as function optimization problems whose dimensions depend on the number of genes. Therefore, it is not always easy to infer large-scale genetic networks consisting of many genes. The inference method described in this chapter resolves the difficulty in the estimation of these parameters by dividing the inference problem into N subproblems first. The method then defines each subproblem as a two-dimensional function optimization problem. As the defined subproblems seem to be multimodal, it uses the evolutionary algorithm, REX![]() /JGG, as a function optimizer. The experimental results showed that the inference method has an ability to infer reasonable genetic networks. The network inferred by the method, however, seemed to still contain a number of false-positive regulations. In addition, its computation times were not always sufficiently short. In future work, the author must deal with these drawbacks.
/JGG, as a function optimizer. The experimental results showed that the inference method has an ability to infer reasonable genetic networks. The network inferred by the method, however, seemed to still contain a number of false-positive regulations. In addition, its computation times were not always sufficiently short. In future work, the author must deal with these drawbacks.
A variety of inference methods based on a variety of mathematical models have been proposed. However, we still do not know which method is most suitable for the inference of genetic networks. The author thinks that, in order to obtain a reliable network, it is important to analyze the measurement data using multiple inference methods based on different models. Kimura et al. have therefore proposed several inference methods based on several mathematical models [20, 21, 23]. The development of a technique to integrate the results obtained from multiple inference methods is also a future goal.
ACKNOWLEDGEMENTS
The author thanks Dr Mariko Okada-Hatakeyama of RIKEN Center for Integrative Medical Sciences and Dr Masanao Sato of National Institute for Natural Sciences for their useful suggestions and comments, and the editors for reviewing the draft of this chapter. Our inference method used a software, BPMPD, developed by Dr Csaba Mészáros at MTA SZTAKI to solve the linear programming problems. This work was partially supported by JSPS KAKENHI Grant Number 26330275.
REFERENCES
- Y. Akimoto, J. Sakuma, I. Ono, and S. Kobayashi. Adaptation of expansion rate for real-coded crossovers. In: Proceedings of 2009 Genetic and Evolutionary Computation Conference, ACM Press, New York, NY, 739–746 (2009).
- T. Akutsu, S. Miyano, and S. Kuhara. Inferring qualitative relations in genetic networks and metabolic pathways, Bioinformatics, 16: 727–734 (2000).
- S. Baluja. Population-based incremental learning, Technical Report CMU-CS-94-163, Carnegie Mellon University, Pittsburgh, PA (1994).
- M. Bansal and D. di Bernardo. Inference of gene networks from temporal gene expression profiles. IET Syst. Biol., 1: 306–312 (2007).
- N. Chemmangattuvalappil, K. Task, and I. Banerjee. An integer optimization algorithm for robust identification of non-linear gene regulatory networks. BMC Systems Biology, 6: 119 (2012).
- D.Y. Cho, K.H. Cho, and B.T. Zhang. Identification of biochemical networks by s-tree based genetic programming. Bioinformatics, 22: 1631–1640 (2006).
- I.C. Chou, H. Martens, and E.O. Voit. Parameter estimation in biochemical systems models with alternating regression. Theoretical Biology and Medical Modelling, 3: 25 (2006).
- I.C. Chou and E.O. Voit. Recent development in parameter estimation and structure identification of biochemical and genomic systems. Mathematical Biosciences, 219: 57–83 (2009).
- W.S. Cleveland. Robust locally weight regression and smoothing scatterplots. Journal of American Statistical Association, 79: 829–836 (1979).
- P. D’haeseleer, S. Liang, and R. Somogyi. Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics, 16: 707–726 (2000).
- A. Ergün, C.A. Lawrence, M.A. Kohanski, T.A. Brennan, and J.J. Collins. A network biology approach to prostate cancer. Molecular Systems Biology, 3: 82 (2007).
- J.J. Faith, B. Hayete, J.T. Thaden, I. Mogno, J. Wierzbowski, G. Cottarel, S. Kasif, J.J. Collins, and T.S. Gardner. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biology, 5: e8 (2007).
- N. Friedman, M. Linial, I. Nachman, and D. Pe’er. Using Bayesian networks to analyze expression data. Journal of Computational Biology, 7: 601–620 (2000).
- T.S. Gardner, D. di Bernardo, D. Lorenz, and J.J. Collins. Inferring genetic networks and identifying compound mode of action via expression profiling. Science, 301: 102–105 (2003).
- P.J.E. Goss and J. Peccoud. Quantitative modeling of stochastic systems in molecular biology by using stochastic petri nets. Proceedings of National Academy of Sciences of the United States of America, 95: 6750–6755 (1998).
- S. Kabir, N. Noman, and H. Iba. Reverse engineering gene regulatory network from microarray data using linear time-variant model. BMC Bioinformatics, 11: S56 (2010).
- S.A. Kauffman. Metabolic stability and epigenesis in randomly constructed genetic nets. Journal of Theoretical Biology, 22: 437–467 (1969).
- S. Kikuchi, D. Tominaga, M. Arita, K. Takahashi, and M. Tomita. Dynamic modeling of genetic networks using genetic algorithm and S-system. Bioinformatics, 19: 643–650 (2003).
- S. Kimura, D. Araki, K. Matsumura, and M. Okada-Hatakeyama. Inference of S-system models of genetic networks by solving one-dimensional function optimization problems Mathematical Biosciences, 235: 161–170 (2012).
- S. Kimura, K. Ide, A. Kashihara, M. Kano, M. Hatakeyama, R. Masui, N. Nakagawa, S. Yokoyama, S. Kuramitsu, and A. Konagaya. Inference of S-system models of genetic networks using a cooperative coevolutionary algorithm. Bioinformatics, 21: 1154–1163 (2005).
- S. Kimura, S. Nakayama, and M. Hatakeyama. Genetic network inference as a series of discrimination tasks. Bioinformatics, 25: 918–925 (2009).
- S. Kimura, M. Sato, and M. Okada-Hatakeyama. Inference of Vohradský’s models of genetic networks by solving two-dimensional function optimization problems. PLoS One, 8: e83308 (2013).
- S. Kimura, K. Sonoda, S. Yamane, H. Maeda, K. Matsumura, and M. Hatakeyama. Function approximation approach to the inference of reduced NGnet models of genetic networks. BMC Bioinformatics, 9: 23 (2008).
- P.K. Liu and F.S. Wang. Inference of biochemical network models in S-system using multiobjective optimization approach. Bioinformatics, 24: 1085–1092 (2008).
- A.A. Margolin, I. Nemenman, K. Basso, C. Wiggins, G. Stolovitzky, R. Dalla Favera, and A. Califano. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics, 7: S7 (2006).
- S. Mehrotra. On the implementation of a primal-dual interior point method. SIAM Journal on Optimization, 2: 575–601 (1992).
- M. Nakatsui, T. Ueda, Y. Maki, I. Ono, and M. Okamoto. Method for inferring and extracting reliable genetic interactions from time-series profile of gene expression. Mathematical Biosciences, 215: 105–114 (2008).
- L. Palafox and H. Iba. On the use of population based incremental learning to do reverse engineering on gene regulatory networks. In: Proceedings of 2012 Congress on Evolutionary Computation, IEEE Publishing, Piscataway, NJ, 1865–1872 (2012).
- W. Press, S. Teukolsky, W. Vetterling, and B. Flannery. Numerical Recipes in C, 2nd edn, Cambridge University Press, Cambridge (1995).
- M. Ronen, R. Rosenberg, B.I. Shraiman, and U. Alon. Assigning numbers to the arrows: parameterizing a gene regulation network by using accurate expression kinetics. Proceedings of National Academy of Sciences of the United States of America, 99: 10555–10560 (2002).
- E. Sakamoto and H. Iba. Inferring a system of differential equations for a gene regulatory network by using genetic programming. In: Proceedings of 2001 Congress on Evolutionary Computation, IEEE Publishing, Piscataway, NJ, 720–726 (2001).
- M.D. Sutton, B.T. Smith, V.G. Godoy, and G.C. Walker. The SOS response: recent insights into umuDC-Dependent mutagenesis and DNA damage tolerance. Annual Review of Genetics, 34: 479–497 (2000).
- D. Thieffry, A.M. Huerta, E. Pérez-Rueda, and J. Collado-Vides. From specific gene regulation to genomic networks: a global analysis of transcriptional regulation in Escherichia coli. BioEssays, 20: 433–440 (1998).
- D. Tominaga and P. Horton. Inference of scale-free networks from gene expression time series. Journal of Bioinformatics and Computational Biology, 4: 503–514 (2006).
- K.Y. Tsai and F.S. Wang. Evolutionary optimization with data collocation for reverse engineering of biological networks. Bioinformatics, 21: 1180–1188 (2005).
- W. Tucker, Z. Kutalik, and V. Moulton. Estimating parameters for generalized mass action models using constraint propagation. Mathematical Biosciences, 208: 607–620 (2007).
- S.R. Veflingstad, J. Almeida, and E.O. Voit. Priming nonlinear searches for pathway identification. Theoretical Biology and Medical Modelling, 1: 8 (2004).
- J. Vohradský. Neural network model of gene expression. FASEB Journal, 15: 846–854 (2001).
- E.O. Voit. Computational Analysis of Biochemical Systems. Cambridge University Press, Cambridge (2000).
- E.O. Voit and J. Almeida. Decoupling dynamical systems for pathway identification from metabolic profiles. Bioinformatics, 20: 1670–1681 (2004).
- R.J. Williams and J. Peng. An efficient gradient-based algorithm for on-line training of recurrent network trajectories. Neural Computation, 2: 490–501 (1990).
- R. Xu, G.K. Venayagamoorthy, and D.C. Wunsch II. Inference of gene regulatory networks with hybrid differential evolution and particle swarm optimization. Neural Networks, 20: 917–927 (2007).
- R. Xu, D.C. Wunsch II, and R.L. Frank. Inference of genetic regulatory networks with recurrent neural network models using particle swarm optimization. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 4: 681–692 (2007).
- M.K.S. Yeung, J. Tegnér, and J.J. Collins. Reverse engineering gene networks using singular value decomposition and robust regression. Proceedings of National Academy of Sciences of the United States of America, 99: 6163–6168 (2002).
- J. Yu, V.A. Smith, P.P. Wang, J. Hartemink, and E.D. Jarvis. Advances to Bayesian network inference for generating causal networks from observational biological data. Bioinformatics, 20: 3594–3603 (2004).








