10
Fourier Analysis: Signals and Filters
In Unit I of this chapter we examine Fourier series and Fourier transforms, two standard tools for decomposing periodic and nonperiodic motions. We find that as implemented for numerical computation, both the series and the integral become a discrete Fourier transform (DFT), which is simple to program. In Unit II we discuss the subject of signal filtering and see that various Fourier tools can be used to reduce noise in measured or simulated signals. In Unit III we present a discussion of the fast Fourier transform (FFT), a technique that is so efficient that it permits evaluations of DFTs in real time.
10.1 Unit I. Fourier Analysis of Nonlinear Oscillations
Consider a particle oscillating in the nonharmonic potential of equation (9.4):
for p = 2, or for the perturbed harmonic oscillator (9.2),

While free oscillations in these potentials are always periodic, they are not truly sinusoidal. Your problem is to take the solution of one of these nonlinear oscillators and relate it to the solution
![]()
of the linear harmonic oscillator. If your oscillator is sufficiently nonlinear to behave like the sawtooth function (Figure 10.1 left), then the Fourier spectrum you obtain should be similar to that shown on the right in Figure 10.1.
In general, when we undertake such a spectral analysis, we want to analyze the steady-state behavior of a system. This means that the initial transient behavior has had a chance to die out. It is easy to identify just what the initial transient is for linear systems but may be less so for nonlinear systems in which the “steady state” jumps among a number of configurations.

Figure 10.1 Left: A sawtooth function in time. Right: The Fourier spectrum of frequencies in natural units contained in this sawtooth function.
10.2 Fourier Series (Math)
Part of our interest in nonlinear oscillations arises from their lack of study in traditional physics courses even though linear oscillations are just the first approximation to a naturally oscillatory system. If the force on a particle is always toward its equilibrium position (a restoring force), then the resulting motion will be periodic but not necessarily harmonic. A good example is the motion in a highly anharmonic well p 10 that produces an x(t) looking like a series of pyramids; this motion is periodic but not harmonic.
In numerical analysis there really is no distinction between a Fourier integral and a Fourier series because the integral is always approximated as a finite series. We will illustrate both methods. In a sense, our approach is the inverse of the traditional one in which the fundamental oscillation is determined analytically and the higher-frequency overtones are determined by perturbation theory [L&L,M 76]. We start with the full (numerical) periodic solution and then decompose it into what may be called harmonics. When we speak of fundamentals, overtones, and harmonics, we speak of solutions to the linear boundary-value problem, for example, of waves on a plucked violin string. In this latter case, and when given the correct conditions (enough musical skill), it is possible to excite individual harmonics or sums of them in the series
Anharmonic oscillators vibrate at a single frequency (which may vary with amplitude) but not with a sinusoidal waveform. Expanding the oscillations in a Fourier series does not imply that the individual harmonics can be excited (played).
You may recall from classical mechanics that the general solution for a vibrating system can be expressed as the sum of the normal modes of that system. These expansions are possible because we have linear operators and, subsequently, the principle of superposition: If y1(t) and y2(t) are solutions of some linear equation, then α1y1(t) + α2y2(t) is also a solution. The principle of linear superposition does not hold when we solve nonlinear problems. Nevertheless, it is always possible to expand aperiodic solution ofa nonlinear problem in terms of trigonometric functions with frequencies that are integer multiples of the true frequency of the nonlinear oscillator.1 This is a consequence of Fourier’s theorem being applicable to any single-valued periodic function with only a finite number of discontinuities. We assume we know the period T, that is, that
A periodic function (usually called the signal) can be expanded as a series of harmonic functions with frequencies that are multiples of the true frequency:

This equation represents the signal y(t) as the simultaneous sum of pure tones of frequency nω. The coefficients an and bn are measures of the amount of cos nωt and sinnωt present in y(t), specifically, the intensity or power at each frequency is proportional to a 2 n + b 2 n.
The Fourier series (10.7) is a best fit in the least-squares sense of Chapter 8, “Solving Systems of Equations with Matrices; Data Fitting,” because it minimizes Si[y(ti) — yi]2, where i denotes different measurements of the signal. This means that the series converges to the average behavior of the function but misses the function at discontinuities (at which points it converges to the mean) or at sharp corners (where it overshoots). Ageneral function y(t) may contain an infinite number of Fourier components, although low-accuracy reproduction is usually possible with a small number of harmonics.
The coefficients an and bn are determined by the standard techniques for function expansion. To find them, multiply both sides of (10.7) by cos nωt or sin nωt, integrate over one period, and project a single an or bn:

As seen in the bn coefficients (Figure 10.1 right), these coefficients usually decrease in magnitude as the frequency increases and can occur with a negative sign, the negative sign indicating relative phase.
Awareness of the symmetry of the function y(t)may eliminate the need to evaluate all the expansion coefficients. For example,
• a0 is twice the average value of y:
• For an odd function, that is, one for which y(- t) = -y(t), allof the coefficients an ≡ 0 and only half of the integration range is needed to determine bn:

However, if there is no input signal for t < 0, we do not have a truly odd function, and so small values of an may occur.
• For an even function, that is, one for which y(-t) = y(t), the coefficient bn ≡ 0 and only half the integration range is needed to determine an:

10.2.1 Example 1: Sawtooth Function
The sawtooth function (Figure 10.1) is described mathematically as

It is clearly periodic, nonharmonic, and discontinuous. Yet it is also odd and so can be represented more simply by shifting the signal to the left:

Even though the general shape of this function can be reproduced with only a few terms of the Fourier components, many components are needed to reproduce the sharp corners. Because the function is odd, the Fourier series is a sine series and (10.8) determines the values
10.2.2 Example 2: Half-wave Function
The half-wave function

is periodic, nonharmonic (the upper half of a sine wave), and continuous, but with discontinuous derivatives. Because it lacks the sharp corners of the sawtooth function, it is easier to reproduce with a finite Fourier series. Equation (10.8) determines

10.3 Exercise: Summation of Fourier Series
1. Sawtooth function: Sum the Fourier series for the sawtooth function up to order n = 2,4,10,20 and plot the results over two periods.
a. Check that in each case the series gives the mean value of the function at the points of discontinuity.
b. Check that in each case the series overshoots by about 9% the value of the function on either side of the discontinuity (the Gibbs phenomenon).
2. Half-wave function: Sum the Fourier series for the half-wave function up to order n = 2,4,10 and plot the results over two periods. (The series converges quite well, doesn’t it?)
![]()
10.4 Fourier Transforms (Theory)
Although a Fourier series is the right tool for approximating or analyzing periodic functions, the Fourier transform or integral is the right tool for nonperiodic functions. We convert from series to transform by imagining a system described by a continuum of “fundamental” frequencies. We thereby deal with wave packets containing continuous rather than discrete frequencies.2 While the difference between series and transform methods may appear clear mathematically, when we approximate the Fourier integral as a finite sum, the two become equivalent.
By analogy with (10.7), we now imagine our function or signal y(t) expressed in terms of a continuous series of harmonics:
where for compactness we use a complex exponential function.3 The expansion amplitude Y (ω) is analogous to the Fourier coefficients (an, bn) and is called the Fourier transformofy(t). The integral (10.17)isthe inverse transform sinceitconverts the transform to the signal. The Fourier transform converts y(t) to its transform Y (ω):

√ The 1/ 2π factor in both these integrals is a common normalization in quantum mechanics but maybe not in engineering where only a single 1/2π factor is used. Likewise, the signs in the exponents are also conventions that do not matter as long as you maintain consistency.
If y(t) is the measured response of a system (signal) as a function of time, then Y (ω) is the spectral function that measures the amount of frequency ω present in the signal. [However, some experiments may measure Y (ω) directly, in which case an inverse transform is needed to obtain y(t).] In many cases Y (ω) is a complex function with positive and negative values and with significant variation in magnitude. Accordingly, it is customary to eliminate some of the complexity of Y (ω) by making a semilog plot of the squared modulus |Y (ω)|2 versus ω. This is called a power spectrum and provides you with an immediate view of the amount of power or strength in each component.
If the Fourier transform and its inverse are consistent with each other, we should be able to substitute (10.17) into (10.18) and obtain an identity:
For this to be an identity, the term in braces must be the Dirac delta function:

While the delta function is one of the most common and useful functions in theoretical physics, it is not well behaved in a mathematical sense and misbehaves terribly in a computational sense. While it is possible to create numerical approximations to δ(ω’ — ω), they may well be borderline pathological. It is certainly better for you to do the delta function part of an integration analytically and leave the nonsingular leftovers to the computer.
10.4.1 Discrete Fourier Transform Algorithm
If y(t) or Y (ω) is known analytically or numerically, the integral (10.17) or (10.18) can be evaluated using the integration techniques studied earlier. In practice, the signal y(t) is measured at just a finite number N of times t, and these are what we must use to approximate the transform. The resultant discrete Fourier transform is an approximation both because the signal is not known for all times and because we integrate numerically4 Once we have a discrete set of transforms, they can be used to reconstruct the signal for any value of the time. In this way the DFT can be thought of as a technique for interpolating, compressing and extrapolating data.
We assume that the signal y(t) is sampled at (N +1) discrete times (N time intervals), with a constant spacing h between times:

In other words, we measure the signal y(t) once every hth of a second for a total time T. This corresponds to period T and sampling rate s:

Regardless of the actual periodicity of the signal, when we choose a period T over which to sample, the mathematics produces a y(t) that is periodic with period T,
We recognize this periodicity, and ensure that there are only N independent measurements used in the transform, by requiring the first and last y’s to be the same:
![]()
If we are analyzing a truly periodic function, then the first N points should all be within one period to guarantee their independence. Unless we make further assumptions, these N independent input data y(tk) can determine no more than N independent output Fourier components Y (ωk).
The time interval T (which should be the period for periodic functions) is the largest time over which we consider the variation of y(t). Consequently, it determines the lowest frequency,

contained in our Fourier representation of y(t). The frequencies ωn are determined by the number of samples taken and by the total sampling time T = Nh as

Here ω0 = 0 corresponds to the zero-frequency or DC component.
The DFT algorithm results from (1) evaluating the integral in (10.18) not from -∞ to +∞ but rather from time 0 to time T over which the signal is measured, and from (2) using the trapezoid rule for the integration5

To keep the final notation more symmetric, the step size h is factored from the transform Y and a discrete function Yn is defined:
With this same care in accounting, and with dω → 2π/N h, we invert the Yn’s:

Once we know the N values of the transform,we can use (10.30) to evaluate y(t) for any time t. There is nothing illegal about evaluating Yn and yk for arbitrarily large values of n and k, yet there is also nothing to be gained. Because the trigonometric functions are periodic, we just get the old answer:
![]()
Another way of stating this is to observe that none of the equations change if we replace ωnt by ωnt+2πn. There are still just N independent output numbers for N independent inputs.
We see from (10.26) that the larger we make the time T = Nh over which we sample the function, the smaller will be the frequency steps or resolution.6 Accordingly, if you want a smooth frequency spectrum, you need to have a small frequency step 2π/T. This means you need alarge value for the total observation time T. While the best approach would be to measure the input signal for longer times, in practice a measured signaly(t)isoftenextendedintime (“padded”)byadding zeros fortimes beyond the last measured signal, which thereby increases the value of T. Although this does not add new information to the analysis, it does build in the experimentalist’s belief that the signal has no existence at times after the measurements are stopped.
While periodicity is expected for Fourier series, it is somewhat surprising for Fourier integrals, which have been touted as the right tool for nonperiodic functions. Clearly, if we input values of the signal for longer lengths of time, then the inherent period becomes longer, and if the repeat period is very long, it may be of little consequence for times short compared to the period. If y(t) is actually periodic with period Nh, then the DFT is an excellent way of obtaining Fourier series. If the input function is not periodic, then the DFT can be a bad approximation near the endpoints of the time interval (after which the function will repeat) or, correspondingly, for the lowest frequencies.
The discrete Fourier transform and its inverse can be written in a concise and insightful way, and be evaluated efficiently, by introducing a complex variable Z for the exponential and then raising Z to various powers:
where Znk ≡ [(Z)n]k. With this formulation, the computer needs to compute only powers of Z. We give our DFT code in Listing 10.1. If your preference is to avoid complex numbers, we can rewrite (10.32) in terms of separate real and imaginary parts by applying Euler’s theorem:

Readers new to DFTs are often surprised when they apply these equations to practical situations and end up with transforms Y having imaginary parts, even though the signal y is real. Equation (10.35) shows that a real signal (Im yk = 0) will yield an imaginary transform unless ¿^k=1sin(nkθ)Re yk =0. This occurs only if y(t) is an even function over —oo < t < +oo and we integrate exactly. Because neither condition holds, the DFTs of real, even functions may have small imaginary parts. This is not due to an error in programming and in fact is a good measure of the approximation error in the entire procedure.
The computation time for a discrete Fourier transform can be reduced even further by use of the fast Fourier transform algorithm. An examination of (10.32) shows that the DFT is evaluated as a matrix multiplication of a vector of length N containing the Z values by a vector of length N of y value. The time for this DFT scales like N2, while the time for the FFT algorithm scales as N log2 N. Although this may not seem like much of a difference, for N = 102-3, the difference of 103-5 is the difference between a minute and a week. For this reason, FFT is often used for on-line analysis of data. We discuss FFT techniques in §10.8.
Listing 10.1 DFT.java computes the discrete Fourier transform for the signal given in the method f(signal []). You will have to add output and plotting to see the results. (The instructor’s version also does an inverse transform and plots the results with PtPlot.)
10.4.2 Aliasing and Anti-aliasing (Assessment) 
The sampling of a signal by DFT for only a finite number of times limits the accuracy of the deduced high-frequency components present in the signal. Clearly good information about very high frequencies requires sampling the signal with small time steps so that all the wiggles can be included. While a poor deduction of the high-frequency components may be tolerable if all we care about are the low-frequency ones, the high-frequency components remain present in the signal and may contaminate the low-frequency components that we deduce. This effect is called aliasing and is the cause of the moiré pattern distortion in digital images.

Figure 10.2 A plot of the functions sin(πt/2) and sin(2πt). If the sampling rate is not high enough, these signals will appear indistinguishable. If both are present in a signal (e.g., as a signal that is the sum of the two) and if the signal is not sampled at a high enough rate, the deduced low-frequency component will be contaminated by the higher-frequency component.
As an example, consider Figure 10.2 showing the two functions sin(πt/2) and sin(2πt) for 0 < t < 8, with their points of overlap in bold. If we were unfortunate enough to sample a signal containing these functions at the times t = 0,2,4, 6, 8, then we would measure y = 0 and assume that there was no signal at all. However, if we were unfortunate enough to measure the signal at the filled dots in Figure 10.2 where sin(πt/2) = sin(2πt), specifically, t = 0, , |,…, then our Fourier analysis would completely miss the high-frequency component. In DFT jargon, we would say that the high-frequency component has been aliased by the low-frequency component. In other cases, some high-frequency values may be included in our sampling of the signal, but our sampling rate may not be high enough to include enough of them to separate the high-frequency component properly. In this case some high-frequency signals would be included spuriously as part of the low-frequency spectrum, and this would lead to spurious low-frequency oscillations when the signal is synthesized from its Fourier components.
More precisely, aliasing occurs when a signal containing frequency f is sampled at a rate of s = N/T measurements per unit time, with s < f/2. In this case, the frequencies f and f — 2s yield the same DFT, and we would not be able to determine that there are two frequencies present. That being the case, to avoid aliasing we want no frequencies f > s/2 to be present in our input signal. This is known as the Nyquist criterion. In practice, some applications avoid the effects of aliasing by filtering out the high frequencies from the signal and then analyzing the remaining low-frequency part. (The low-frequency sinc filter discussed in §10.7.1 is often used for this.) Even though this approach eliminates some high-frequency information, it lessens the distortion of the low-frequency components and so may lead to improved reproduction of the signal.
If accurate values for the high frequencies are required, then we will need to increase the sampling rate s by increasing the numberN of samples taken with in the fixed sampling time T = Nh. Bykeeping the sampling time constant and increasing the number ofsamples taken,we make the time step hsmaller, and this picksupthe higher frequencies. By increasing the number N of frequencies that you compute, you move the higher-frequency components you are interested in closer to the middle of the spectrum and thus away from the error-prone ends.
If we vary the the total time sampling time T = Nh but not the sampling rate s = N/T = 1/h, we make ω1 smaller because the discrete frequencies
are measured in steps ofω1. This leads to a smoother frequency spectrum. However, to keep the time step the same and thus not lose high-frequency information, we would also need to increase the number of N samples. And as we said, this is often done, after the fact, by padding the end of the data set with zeros.
10.4.3 DFT for Fourier Series (Algorithm)
For simplicity let us consider the Fourier cosine series:

Here T d=ef 2π/ω is the actual period of the system (not necessarily the period of the simple harmonic motion occurring for a small amplitude). We assume that the function y(t) is sampled for a discrete set of times
![]()
Because we are analyzing a periodic function, we retain the conventions used in the DFT and require the function to repeat itself with period T = Nh; that is, we assume that the amplitude is the same at the first and last points:
![]()
This means that there are only N independent values of y being used as input. For these N independent yk values, we can determine uniquely only N expansion coefficientsak. Ifwe use the trapezoid rule to approximate the integration in (10.38), we determine the N independent Fourier components as
Because we can determine only N Fourier components from N independent y(t) values, our Fourier series for the y(t) must be in terms of only these components:

In summary, we sample the function y(t) at N times, t1,. . ., tN. We see that all the values of y sampled contribute to each ak. Consequently, if we increase N in order to determine more coefficients, we must recompute all the an values. In the waveletanalysisinChapter 11, “WaveletAnalysis&Data Compression,”thetheory is reformulated sothat additional samplings determine higher Fourier components without affecting lower ones.
10.4.4 Assessments
Simple analytic input: It is always good to do these simple checks before examining more complex problems. If your system has some Fourier analysis packages (such as the graphing package Ace/gr), you may want to compare your results with those from the packages. Once you understand how the packages work, it makes sense to use them.
1. Sample the even signal
![]()
Decompose this into its components; then check that they are essentially real and in the ratio 3:2:1 (or 9:4:1 for the power spectrum) and that they resum to give the input signal.
2. Experiment on the separate effects of picking different values of the step size h and of enlarging the measurement period T = Nh.
3. Sample the odd signal
![]()
Decompose this into its components; then check that they are essentially imaginary and in the ratio 1:2:3 (or 1:4:9 if a power spectrum is plotted) and that they resum to give the input signal.
4. Sample the mixed-symmetry signal
![]()
Decompose this into its components; then check that there are three of them in the ratio 5:2:1 (or 25:4:1 if a power spectrum is plotted) and that they resum to give the input signal.
5. Sample the signal
Compare and explain the results obtained by sampling (a) without the 5, (b) as given but without the 2, and (c) without the 5 and without the 2.
6. In our discussion of aliasing, we examined Figure 10.2 showing the functions sin(πt/2) and sin(2πt). Sample the function
![]()
and explore how aliasing occurs. Explicitly, we know that the true transform contains peaks at ω = π/2 and ω = 2π. Sample the signal at a rate that leads to aliasing, as well as at a higher sampling rate at which there is no aliasing. Compare the resulting DFTs in each case and check if your conclusions agree with the Nyquist criterion.
![]()
Highly nonlinear oscillator: Recall the numerical solution for oscillations of a spring with power p = 12 [see (10.1)]. Decompose the solution into a Fourier series and determine the number of higher harmonics that contribute at least 10%;for example, determine thenfor which|bn/b1| < 0.1.Checkthatresuming the components reproduces the signal.
Nonlinearly perturbed oscillator: Remember the harmonic oscillator with a nonlinear perturbation (9.2):

For very small amplitudes of oscillation (x <C 1/α), the solution x(t) will essentially be only the first term of a Fourier series.
1. We want the signal to contain “approximately 10% nonlinearity.” This being the case, fix your value of α so that αxmax c; 10%, where xmax is the maximum amplitude of oscillation. For the rest of the problem, keep the value of α fixed.
2. Decompose your numerical solution into a discrete Fourier spectrum.
3. Plot a graph of the percentage of importance of the first two, non-DC Fourier components as a function of the initial displacement for 0 < x0 < 1/2α. You should find that higher harmonics are more important as the amplitude increases. Because both even and odd components are present, Yn should be complex. Because a 10% effect in amplitude becomes a 1% effect in power, make sure that you make a semilog plot of the power spectrum.
4. As always, check that resumations of your transforms reproduce the signal.
(Warning: The ω you use in your series must correspond to the true frequency of the system, not just the ω of small oscillations.)
10.4.5 DFT of Nonperiodic Functions (Exploration)
Consider a simple model (a wave packet) of a “localized” electron moving through space and time. A good model for an electron initially localized around x = 5 is a Gaussian multiplying a plane wave:
This wave packet is not an eigenstate of the momentum operator7 p = id/dx and in fact contains a spread of momenta. Your problem is to evaluate the Fourier transform,

as a way of determining the momenta components in (10.44).
10.5 Unit II. Filtering Noisy Signals
You measure a signal y(t) that obviously contains noise. Your problem is to determine the frequencies that wouldbepresentinthe signalifitdid not contain noise. Of course, once you have a Fourier transform from which the noise has been removed, you can transform it to obtain a signal s(t) with no noise.
In the process of solving this problem we examine two simple approaches: the use of autocorrelation functions and the use of filters. Both approaches find wide applications in science, with our discussion not doing the subjects justice. However, we will see filters again in the discussion of wavelets in Chapter 11, “Wavelet Analysis & Data Compression.”
10.6 Noise Reduction via Autocorrelation (Theory)
We assume that the measured signal is the sum of the true signal s(t), which we wish to determine, plus the noise n(t):
![]()
Our first approach to separating the signal from the noise relies on that fact that noise is a random process and thus should not be correlated with the signal. Yet what do we mean when we say that two functions are correlated? Well, if the two tend to oscillate with their nodes and peaks in much the same places, then the two functions are clearly correlated. An analytic measure of the correlation of two arbitrary functions y(t) and x(t) is the correlation function
where τ, the lag time, is a variable. Even if the two signals have different magnitudes, if they have similar time dependences except for one lagging or leading the other, then for certain values of τ the integrand in (10.47) will be positive for all values of t. In this case the two signals interfere constructively and produce a large value for the correlation function. In contrast, if both functions oscillate independently, then it is just as likely for the integrand to be positive as to be negative, in which case the two signals interfere destructively and produce asmall value for the integral.
Before we apply the correlation function to our problem, let us study some of its properties.Weuse (10.17)to express c, y∗, and xin terms of their Fourier transforms:

Because ω, ω’, and ω” are dummy variables, other names may be used for these variables without changing any results. When we substitute these representations into the definition (10.47) and assume that the resulting integrals converge well enough to be rearranged, we obtain

where the last line follows because ω” and ω are equivalent dummy variables. Equation (10.49) says that the Fourier transform of the correlation function between two signals is proportional to the product of the transform of one signal and the complex conjugate of the transform of the other. (We shall see a related convolution theorem for filters.)
A special case of the correlation function c(τ) is the autocorrelation function A(τ). It measures the correlation of a time signal with itself:
This function is computed by taking a signal y(t) that has been measured over some time period and then averaging it over time using y(t+τ) as a weighting function. This process is also called folding a function onto itself (as might be done with dough) or a convolution. To see how this folding removes noise from a signal, we go back to the measured signal (10.46), which was the sum of pure signal plus noise s(t)+n(t). As an example, on the upper left in Figure 10.3 we show a signal that was constructed by adding random noise to a smooth signal. When we compute the autocorrelation function for this signal, we obtain afunction (upper right in Figure 10.3) that looks like a broadened, smoothed version of the signal y(t). We can understand how the noise is removed by taking the Fourier transform of s(t)+n(t) to obtain a simple sum of transforms:

Because the autocorrelation function (10.50) for y(t) = s(t) + n(t) involves the second power of y, is not a linear function, that is, Ay = As +An, but instead,

If we assume that the noise n(t) in the measured signal is truly random, then it should average to zero over long times and be uncorrelated at times t and t+τ. This being the case, both integrals involving the noise vanish, and so

Thus, the part of the noise that is random tends to be averaged out of the autocorrelation function, and we are left with the autocorrelation function of approximately the pure signal.
This is all very interesting but is not the transform S(ω) of the pure signal that we need to solve our problem. However, application of (10.49) with Y (ω) = X(ω) = S(ω) tells us that the Fourier transform A(ω) of the autocorrelation function is proportional to |S(ω)|2:


Figure 10.3 From bottom left to right: The function plus noise s(t)+ n(t), the autocorrelation function versus time, the power spectrum obtained from autocorrelation function,and the noisy signal after passage through a lowpass filter.
The function |S(ω)|2 is the power spectrum we discussed in §10.4. For practical purposes, knowing the power spectrum is often all that is needed and is easier to understand than a complex S(ω); in any case it is all that we can calculate.
As a procedure for analyzing data, we (1) start with the noisy measured signal and (2) compute its autocorrelation function A(t) via the integral (10.50). Because this is just folding the signal onto itself, no additional functions or input is needed. We then (3) perform a DFT on the autocorrelation function A(t) to obtain the power spectrum. For example, in Figure 10.3 we see a noisy signal (lower left), the autocorrelation function (lower right), which clearly is smoother than the signal, and finally, the deduced power spectrum (upper left). Notice that the broadband high-frequency components characteristic of noise are absent from the power spectrum. You can easily modify the sample program DFT.java in Listing 10.1 to compute the autocorrelation function and then the power spectrum from A(τ). We present a program NoiseSincFilter or Filter.java that does this on the CD (available online: http://press.princeton.edu/landau_survey/).
10.6.1 Autocorrelation Function Exercises
1. Imagine that you have sampled the pure signal

Figure 10.4 Input signal f is filtered by h, and the output is g.
Although there is just a single sine function in the denominator, there is an infinite number of overtones as follows from the expansion
a. Compute the DFT S(ω). Make sure to sample just one period but to cover the entire period. Make sure to sample at enough times (fine scale) to obtain good sensitivity to the high-frequency components.
b. Make a semilog plot of the power spectrum |S(ω)|2.
c. Take your input signal s(t) and compute its autocorrelation function A(τ) for a full range of τ values (an analytic solution is okay too).
d. Compute the power spectrum indirectly by performinga DFT on the auto correlation function. Compare your results to the spectrum obtained by computing |S(ω)|2 directly.
2. Add some random noise to the signal using a random number generator:
![]()
whereα is an adjustable parameter. Try several values of α, from small values that just add some fuzz to the signal to large values that nearly hide the signal.
a. Plot your noisy data, their Fourier transform, and their power spectrum obtained directly from the transform with noise.
b. Compute the autocorrelation function A(t) and its Fourier transform.
c. Compare the DFT of A(τ) to the power spectrum and comment on the effectiveness of reducing noise by use of the autocorrelation function.
d. For what value of α do you essentially lose all the information in the input?
![]()
The code Noise.java that performs similar steps is available on the CD (available online: http://press.princeton.edu/landau_survey/).
10.7 Filtering with Transforms (Theory)
Afilter (Figure 10.4) is a device that converts an input signal f(t) to an output signal g(t) with some specific property for the latter. More specifically, an analog filter is defined [Hart 98] as integration over the input function:
The operation indicated in (10.59) occurs often enough that it is given the name convolution and is denoted by an asterisk ∗. The function h(t) is called the response ortransfer functionof the filter because it is the response of the filterto aunit impulse:
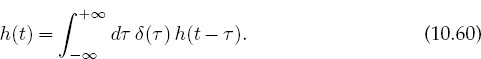
Such being the case, h(t) is also called the unit impulse response function or Green’s function. Equation (10.59) states that the output g(t) of a filter equals the input f(t) convoluted with the transfer function h(t-τ). Because the argument of the response function is delayed by a time τ relative to that of the signal in the integral (10.59), τ is called the lag time. While the integration is over all times, the response of a good detector usually peaks around zero time. In any case, the response must equal zero forτ > tbecause events in the future cannot affect the present (causality).
The convolution theorem states that the Fourier transform of the convolution g(t) is proportional to the product of the transforms of f(t) and h(t):
![]()
The theorem results from expressing the functions in (10.59) by their transforms and using the resulting Dirac delta function to evaluate an integral (essentially what we did in our discussion of correlation functions). This is an example of how some relations are simpler in transform space than in time space.
Regardless of the domain used, filtering as we have defined it is a linear process involving just the first powers of f. This means that the output at one frequency is proportional to the input at that frequency. The constant of proportionality between the two may change with frequency and thus suppress specific frequencies relative to others, but that constant remains fixed in time. Because the law of linear superposition is valid for filters, if the input to a filter is represented as the sum of various functions, then the transform of the output will be the sum of the functions’ Fourier transforms. Because the transfer function may be complex, H(ω) = |H(ω)|exp[iφ(ω)], the filter may also shift the phase of the input at frequency ω by an amount φ.
Filters that remove or decrease high-frequency components more than they do low-frequency components, are called lowpass filters. Those that filter out the low frequencies are called highpass filters. A simple lowpass filter is the RC circuit on the left in Figure 10.5, and it produces the transfer function

where τ = RC is the time constant. The ω2 in the denominator leads to a decrease in the response at high frequencies and therefore makes this a lowpass filter (the

Figure 10.5 Left: An RC circuit arranged as a lowpass filter. Right: An RC circuit arranged as a highpass filter.
iω affects only the phase). A simple highpass filter is the RC circuit on the right in Figure 10.5, and it produces the transfer function
H = 1 at large ω, yet H vanishes as ω → 0, which makes this a highpass filter.
Filters composed of resistors and capacitors are fine for analog signal processing. For digital processing we want a digital filter that has a specific response function for each frequency range. A physical model for a digital filter may be constructed from a delay line with taps at various spacing along the line (Figure 10.6) [Hart 98]. The signal read from tap n is just the input signal delayed by time nτ, where the delay time τ is a characteristic of the particular filter. The output from each tap is described by the transfer function δ(t – nτ), possibly with scaling factor cn. As represented by the triangle on the right in Figure 10.6, the signals from all taps are ultimately summed together to form the total response function:

In the frequency domain, the Fourier transform of a delta function is an exponential, and so (10.64) results in the transfer function

where the exponential indicates the phase shift from each tap.
If a digital filter is given a continuous time signal f(t) as input, its output will be the discrete sum


Figure 10.6 A delay-line filter in which the signal at different time translations is scaled by different amounts ci.
And of course, if the signal’s input is a discrete sum, its output will remain a discrete sum. (We restrict ourselves to nonrecursive filters [Pres 94].) In either case, we see that knowledge of the filter coefficients c¿ provides us with all we need to know about a digital filter. If we look back at our work on the discrete Fourier transform in §10.4.1, we can view a digital filter (10.66) as a Fourier transform in which we use an N -point approximation to the Fourier integral. The cn’s then contain both the integration weights and the values of the response function at the integration points. The transform itself can be viewed as a filter of the signal into specific frequencies.
10.7.1 Digital Filters: Windowed Sinc Filters (Exploration) 
Problem: Construct digital versions of highpass and lowpass filters and determine which filter works better at removing noise from a signal.
A popular way to separate the bands of frequencies in a signal is with a windowed sinc filter [Smi 99]. This filter is based on the observation that an ideal lowpass filter passes all frequencies below a cutoff frequency ωα and blocks all frequencies above this frequency. And because there tends to be more noise at high frequencies than at low frequencies, removing the high frequencies tends to remove more noise than signal, although some signal is inevitably lost. One use for windowed sinc filters is in reducing aliasing by removing the high-frequency component of a signal before determining its Fourier components. The graph on the lower right in Figure 10.7 was obtained by passing our noisy signal through a sinc filter (using the program Filter.java given on the CD (available online: http://press.princeton.edu/landau_survey/)).
If both positive and negative frequencies are included, an ideal low-frequency filter will look like the rectangular pulse in frequency space:

Figure 10.7 Lower left: Frequency response for an ideal lowpass filter. Lower right: Truncated-sinc filter kernel (time domain). Upper left: Windowed-sinc filter kernel. Upper right: windowed-sinc filter frequency response.
Here rect(ω) is the rectangular function (Figure 10.8). Although maybe not obvious, a rectangular pulse in the frequency domain has a Fourier transform that is proportional to the sinc function in the time domain [Smi 91, Wiki]
where the π’s are sometimes omitted. Consequently, we can filter out the high-frequency componentsof asignalby convolutingitwith sin(ωct)/(ωct),atechnique also known as the Nyquist–Shannon interpolation formula. In terms of discrete transforms, the time-domain representation of the sinc filter is

All frequencies below the cut off frequencyωc are passed with unit amplitude, while all higher frequencies are blocked.
In practice, there are a number of problems in using this function as the filter. First, as formulated, the filter is noncausal; that is, there are coefficients at negative times, which is nonphysical because we do not start measuring the signal until t = 0. Second, in order to produce a perfect rectangular response, we would have to sample the signal at an infinite number of times. In practice,we sampleat(M + 1)

Figure 10.8 The rectangle function rect(ω) whose Fourier transform is sinc(t).
points (M even) placed symmetrically around the main lobe of sin(πt)/πt and then shift times to purely positive values,
As might be expected, a penalty is incurred for making the filter discrete; instead of the ideal rectangular response, we obtain a Gibbs overshoot, with rounded corners and oscillations beyond the corner.
There are two ways to reduce the departures from the ideal filter. The first is to increase the length of times for which the filter is sampled, which inevitably leads to longer compute times. The other way is to smooth out the truncation of the sinc function by multiplying it with a smoothly tapered curve like the Hamming window function:

The cutoff frequency ωc should be a fraction of the sampling rate. The time length M determines the bandwidth over which the filter changes from 1 to 0.
Exercise: Repeat the exercise that added random noise to a known signal, this time using the sinc filter to reduce the noise. See how small you can make the signal and still be able to separate it from the noise. (The code Noise.java that performs these steps is on the instructor’s CD (available online: http://press.princeton.edu/landau_survey/).)
10.8 Unit III. Fast Fourier Transform Algorithm
We have seen in (10.32) that a discrete Fourier transform can be written in the compact form
Even if the signal elements yk to be transformed are real, Z is always complex, and therefore we must process both real and imaginary parts when computing transforms. Because both n and k range over N integer values, the (Zn)k yk multiplications in (10.73) require some N2 multiplications and additions of complex numbers. As N gets large, as happens in realistic applications, this geometric increase in the number of steps slows down the algorithm.
In 1965, Cooley and Tukey discovered an algorithm8 that reduces the number of operations necessary to perform a DFT from N2 to roughly N log2 N [Co 65, Donn 05]. Even though this may not seem like such a big difference, it represents a 100-fold speedup for 1000 data points, which changes a full day of processing into 15 min of work. Because of its widespread use (including cell phones), the fast Fourier transform algorithm is considered one of the 10 most important algorithms of all time.
The idea behind the FFT is to utilize the periodicity inherent in the definition of the DFT (10.73) to reduce the total number of computational steps. Essentially, the algorithm divides the input data into two equal groups and transforms only one group, which requires ∼ (N/2)2 multiplications. It then divides the remaining (nontransformed) group of data in half and transforms them, continuing the process until all the data have been transformed. The total number of multiplications required with this approach is approximately N log2 N.
Specifically, the FFT’s time economy arises from the computationally expensive complex factor Znk[= ((Z)n)k] being equal to the same cyclically repeated value as the integers n and k vary sequentially. For instance, for N = 8,

where we include Z0(≡1) for clarity. When we actually evaluate these powers of Z, we find only four independent values:

When substituted into the definitions of the transforms, we obtain

We see that these transforms now require 8×8 = 64 multiplications of complex numbers, in addition to some less time-consuming additions. We place these equations in an appropriate form for computing by regrouping the terms into sums and differences of the y’s:
![]()

Figure 10.9 The basic butterfly operation in which elements yp and yq are transformed into yp +Z yq and yp -Z yq.
Note the repeating factors inside the parentheses, with combinations of the form yp ±yq. These symmetries are systematized by introducing the butterfly operation (Figure 10.9). This operation takes the yp and yq data elements from the left wing and converts them to the yp +Zyq elements in the upper- and lower-right wings. In Figure 10.10 we show what happens when we apply the butterfly operations to an entire FFT process, specifically to the pairs (y0, y4), (y1, y5), (y2, y6), and (y3, y7). Notice how the number of multiplications of complex numbers has been reduced: For the first butterfly operation there are 8 multiplications by Z0; for the second butterfly operation there are 8 multiplications, and so forth, until a total of 24 multiplications is made in four butterflies. In contrast, 64 multiplications are required in the original DFT (10.8).
10.8.1 Bit Reversal
The reader may have observed that in Figure 10.10 we started with 8 data elements in the order 0–7 and that after three butterfly operators we obtained transforms in the order 0, 4, 2, 6, 1, 5, 3, 7. The astute reader may may also have observed that these numbers correspond to the bit-reversed order of 0–7.

Figure 10.10 The butterfly operations performing a FFT on four pairs of data.
Let us look into this further. We need 3 bits to give the order of each of the 8 input data elements (the numbers 0–7). Explicitly, on the left in Table 10.1 we give the binary representation for decimal numbers 0–7, their bit reversals, and the corresponding decimal numbers. On the right we give the ordering for 16 input data elements, where we need 4 bits to enumerate their order. Notice that the order of the first 8 elements differs in the two cases because the number of bits being reversed differs. Notice too that after the reordering, the first half of the numbers are all even and the second half are all odd.
The fact that the Fourier transforms are produced in an order corresponding to the bit-reversed order of the numbers 0–7 suggests that if we process the data in the bit-reversed order 0, 4, 6, 2, 1, 5, 3, 7, then the output Fourier transforms will be ordered.We demonstrate this conjecture in Figure 10.11, where we see that to obtain the Fourier transform for the 8 input data, the butterfly operation had to be applied 3 times. The number 3 occurs here because it is the power of 2that gives the number of data; that is, 23 = 8. In general, in order for a FFT algorithmto produce transforms in the proper order,itmust reshuffle the input data into bit-reversed order.Asacase in point, our sample program starts by reordering the 16 (24) data elements given in Table 10.2. Now the 4 butterfly operations produce sequentially ordered output.
10.9 FFT Implementation
The first FFT program weare aware of was written in 1967 in Fortran IV by Norman Brenner at MIT’s Lincoln Laboratory [Hi,76] and was hard for us to follow. Our (easier-to-follow) Java version of it is in Listing 10.2. Its input is N = 2n data to be transformed (FFTs always require 2N input data). If the number of your input data is not a power of 2, then you can make it so by concatenating some of the initial data to the end of your input until a power of 2 is obtained; since a DFT is always periodic, this just starts the period a little earlier. This program assigns complex numbers at the 16 data points
![]()
reorders the data via bit reversal, and then makes four butterfly operations. The data are stored in the array dtr[max][2], with the second subscript denoting real and imaginary parts.We increase speed further by using the 1-D array data to make memory access more direct:
![]()

Figure 10.11 Modified FFT.
which also provides storage for the output. The FFT transforms data using the butterfly operation and stores the results back in dtr[][], where the input data were originally.
TABLE 10.2
Reordering for 16 Data Complex Points
Order |
Input Data |
New Order |
Order |
Input Data |
New Order |
0 |
0.0 + 0.0i |
0.0 + 0.0i |
8 |
8.0 + 8.0i |
1.0 + 1.0i |
1 |
1.0 + 1.0i |
8.0 + 8.0i |
9 |
9.0 + 9.0i |
9.0 + 9.0i |
2 |
2.0 + 2.0i |
4.0 + 4.0i |
10 |
10.0 + 10.i |
5.0 + 5.0i |
3 |
3.0 + 3.0i |
12.0 + 12.0i |
11 |
11.0 + 11.0i |
13.0 + 13.0i |
4 |
4.0 + 4.0i |
2.0 + 2.0i |
12 |
12.0 + 12.0i |
3.0 + 3.0i |
5 |
5.0 + 5.0i |
10.0 + 10.i |
13 |
13.0 + 13.0i |
11.0 + 11.0i |
6 |
6.0 + 6.0i |
6.0 + 6.0i |
14 |
14.0 + 14.i |
7.0 + 7.0i |
7 |
7.0 + 7.0i |
14.0 + 14.0i |
15 |
15.0 + 15.0i |
15.0 + 15.0i |
Listing 10.2 FFT.java computes the FFT or inverse transform depending upon the sign of isign.
10.10 FFT Assessment
1. Compile and execute FFT.java. Make sure you understand the output.
2. Take the output from FFT.java, inverse-transform it back to signal space, and compare it to your input. [Checking that the double transform is proportional to itselfis adequate, although the normalization factorsin(10.32) should make the two equal.]
3. Compare the transforms obtained with a FFT to those obtained with a DFT (you may choose any of the functions studied before). Make sure to compare both precision and execution times.
![]()
1 We remind the reader that every periodic system by definition has a period T and consequently a true frequency ω. Nonetheless, this does not imply that the system behaves like sinωt. Only harmonic oscillators do that.
2 We follow convention and consider time t the function’s variable and frequency ω the transform’s variable. Nonetheless, these canbereversedorother variables suchasposition x and wave vector k may also be used.
3 Recollect the principle of linear superposition and that exp(iωt) = cosωt + isin ωt. This means that the real part of y gives the cosine series, and the imaginary part the sine series.
4 More discussion can be found in [B&H 95], which is devoted to just this topic.
5 The alert reader maybewondering what has happenedtothe h/2 with which the trapezoid rule weights the initial and final points. Actually, they are there, but because we have set y0 ≡ yN, two h/2 terms have been added to produce one h term.
6 See also §10.4.2 where we discuss the related phenomenon of aliasing.
7 We use natural units in which h = l.
8 Actually, this algorithm has been discovered a number of times, for instance, in 1942 by Danielson and Lanczos [Da 42], as well as much earlier by Gauss.


























