• Any group or collection of objects can form a set. The objects in a set are called elements.
• For example, in the set of numbers:
S = {3, 5, 10, 17}
S depicts the set, and 3, 5, 10, and 17 are its elements.
• Because 5 is a member of the Set S, we write:
5 ∊ S
The symbol for member is “∊”.
• Q is a set where, Q = {5, 10}.
Note that Q is also a subset of Set S.
• The symbol for subset is “⊂”, where Q ⊂ S.
• If P is an empty set, we write P = {}.
An empty set is also called a null set.
• An empty set is a subset of every other set, so the following is true:
P ⊂ Q and P ⊂ S
• An alternative method for describing a set is to write:
{x: }
This set contains values for x, which are described by what is written after the colon.
• For example:
{x: x is a quadrilateral}
All members of this set are quadrilaterals (planar four-sided objects), including squares, rectangles, parallelograms, and trapezoids.
• The arrangement of the objects or values in the set does not matter.
Q = {5, 10} = {10, 5}
• Duplicates or replicates of an object or value in a set do not count as extra objects or values and do not change the net value of the set.
Q = {5, 10} = {5, 10, 5} = {5, 10, 10} = {10, 5, 5, 5, 10}
• Combining sets is called a union of the sets. The symbol for union is “∪”.
S ∪ Q = {3, 5, 10, 17} ∪ {5, 10}
= {3, 5, 10, 17, 5, 10} = {3, 5, 10, 17}
• Suppose there are two sets and some of the objects or values in one set are the same as some of the objects or values in the other set. If the objects that are common to both sets are placed in a new set, the new set is called an intersection of the first two sets. The symbol for intersection is “∩”.
Set X = {π, 2, 7}
Set Y = {2, 5, 8}
X ∩ Y = {2}
Venn diagrams are often used to represent sets and their intersection. This is a Venn diagram of X ∩ Y, where set X contains π, 7, and 2, and set Y contains 5, 8, and 2. The intersection of set X and Y is a third set that contains 2.
X ∩ Y =

• In this section, functions, domain set, range set, graphing functions, compound functions, inverse functions, as well as adding, subtracting, multiplying, and dividing functions are described.
• A function is a relation, rule, expression, or equation that associates each element of a domain set with its corresponding element in the range set. For a relation, rule, expression, or equation to be a function, there must be only one element or number in the range set for each element or number in the domain set.
• The domain set is the initial set and the range set is the resulting set when a function is applied.
Domain Set → Function f() → Range Set
• The function f() is like a transformer that translates the domain set into the range set.
• Each time a given member of the domain set goes through the function transformer, it always produces the same member in the range set.
domain set x → function (transformer) f()
→ range set f(x)
For example, domain set x = {2, 3, 4}
through function f(x) = x2,
Where f(2) = 22, f(3) = 32, and f(4) = 42
to range set f(x) = {4, 9, 16}
• The domain set and range set can be expressed as (x, f(x)) pairs. In the previous example, the function is f(x) = x2 and the pairs are (2, 4), (3, 9), and (4, 16).
• For each member of the domain set, there must be only one corresponding member in the range set. For example:
F = (2, 4), (3, 9), (4, 16) Where F is a function.
M = (2,5), (2, –5), (4, 9) Where M is not a function.
M is not a function because the number 2 in the domain set corresponds to more than one number in the range set.
• To graph functions, the values in the domain set correspond to the X-axis and the related values in the range set correspond to the Y-axis.
domain set x = –2, –1, 0, 2
through function f(x) = x + 1
to range set f(x) = –1, 0, 1, 3
resulting in pairs (x, y) = (–2, –1), (–1, 0), (0, 1), (2, 3)
When graphed these resulting pairs are depicted as:
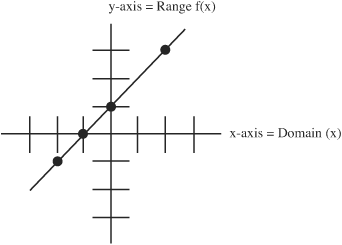
• Graphs of functions only have one value for y for each x value.

If a vertical line can be drawn that passes through the function more than one time, there is more than one y value for a given x value and the graph is not a function. This is called the vertical line test.
• The following are examples of addition, subtraction, multiplication, and division of functions. In these examples the functions f(x) and g(x) are given by:
f(x) = 2x and g(x) = x2
Add two functions:
f(x) + g(x) = (f + g)(x) = 2x + x2
Subtract two functions:
f(x) – g(x) = (f – g)(x) = 2x – x2
Multiply two functions:
f(x) × g(x) = (f × g)(x) = 2x × x2 = 2x3
Divide two functions:
• Compound functions are functions that are combined, and the operations specified by the functions are combined. Compound functions are written:
f(g(x)) or g(f(x))
If f(x) = x + 1 and g(x) = 2x – 2,
then the compound functions for f(g(x)) and g(f(x)) are:
f(g(x)) = f(2x – 2) = (2x – 2) + 1 = 2x – 1 and
g(f(x)) = g(x + 1) = 2(x + 1) – 2 = 2x + 2 – 2 = 2x
The notation for compound functions may also be written:
f ° g and g ° f
• Inverse functions are functions that result in the same value of x after the operations of the two functions are performed. In inverse functions the operations of each function are the reverse of the other function. The notation for inverse is f–1(x). Functions are inverse if:
f(g(x)) = x and g(f(x)) = x
• For example, if f(x) = 2x – 1, find the inverse by solving for x.
Let f(x) = y, the function becomes:
y = 2x – 1
y + 1 = 2x
(y + 1)/2 = x
If y and x are switched, the inverse of f(x) = 2x – 1 is
f–1(x) = (x + 1)/2
To verify that f(x) = and f–1 (x) are inverse functions, let x = 3 and substitute into the functions.
f(x) = 2x – 1 = f(3) = 2(3) – 1 = 6 – 1 = 5
Substitute the result, 5, into f–1(x)
f–1(x) = (x + 1)/2 = f–1(5) = (5 + 1)/2 = 6/2 = 3
The result is 3.
Also, verify the inverse using f(f–1(x)) = 2[(x + 1)/2] – 1:
If x = 3, f(f–1(3)) = 2[(3 + 1)/2] – 1 = 2[2] – 1 = 3
Or using f–1(f(x)) = ([2x – 1] + 1)/2:
If x = 3, f–1(f(3)) = ([2(3) – 1]+ 1)/2 = ([5] + 1)/2 = 3
