7.1. MIMO servers and aggregation of flows

Roughly speaking, a MIMO (multiple inputs, multiple outputs) server is a server crossed by several flows. In the context of network calculus, such a server is still described by a service curve (and a service policy, which will be introduced later in this chapter). A service curve describes the total service offered by the server to the global arrival process. For this reason, we will first define the notion of aggregate flow. Then, we will give a formal definition of a MIMO server in terms of cumulative arrival and departure processes.

7.1.1. Aggregate flow

DEFINITION 7.1 (Aggregate cumulative process).– Let I be a finite set, and for all i ∈ I, let A_i ∈ C be a cumulative arrival process. The aggregate cumulative process of (A_i)_i∈I is

It should be obvious that A ∈ C.

PROPOSITION 7.1 (Arrival curve of an aggregate flow).– Let I be a finite set, and for all i ∈ I, let A_i ∈ C be a cumulative arrival process with respective arrival curve α_i. Then, α = ∑_i∈I α_i is an arrival curve for the aggregate cumulative process ∑_i∈I A_i.

PROOF.– with , hence the result.

□

We note that this formula is not tight: consider the example of Figure 7.1. Set (plain) and (dashed). Then, α =A₁ is an arrival curve for both A₁ and A₂. From the previous proposition, is also an arrival curve for . However, as shown in Figure 7.1, is a better (i.e. smaller) arrival curve for A₁ + A₂. We refer the reader to section 6.3.2.3 for discussion about the modeling of such arrival curves.

PROPOSITION 7.2 (Arrival curve of sub-flow).– If α is an arrival curve for some aggregate cumulative process , then it is also an arrival curve for any A_j, .

This proposition can be useful in at least two cases: first, when only an arrival curve of the aggregate flow has been computed; second, and more importantly, as in [BOY 10a], when the maximum service curve of a server is known, it enables us to use the results of Chapter 5 and improve the arrival curve of the aggregate departure process and thus of each flow.

PROOF.– For all . As A_i are non-decreasing functions, for all .

□

7.1.2. MIMO servers

In this section, we define servers with multiple inputs and multiple outputs. Here, we restrict the definitions to the cases where the number of inputs and outputs are equal. We will discuss the more general case at the end of the section.

DEFINITION 7.2 (MIMO Server).– A server with multiple input and multiple output of dimension n is a relation between vectors of cumulative functions such that . To enforce the dimension of the server, we will call such a server an n-server in the following.

We will indistinctly use the notations or . When focusing on the pair of processes (A_i, D_i), we will use the term flow i. As in the case of servers with a single input and output, we assume that for each flow, data are served in their arrival order (we call this a FIFO-per-flow policy).

If for each there exists a unique such that , then server S is said to be deterministic, otherwise, it is said to be non-deterministic.

DEFINITION 7.3 (Aggregate server).– Let S be an n-server. The aggregate server S_∑ is the server associated with the aggregate processes:

[7.1]

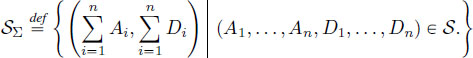
DEFINITION 7.4 (Residual server).– Let S be an n-server. The residual server for flow i is

[7.2]

When focusing on flow i, we call the rest of the flows the cross-traffic.

We remark that, even when considering a deterministic MIMO server, each residual server can be non-deterministic since, in general, one departure process D_i is related to the other processes . This is another reason why the non-deterministic definition of a server is necessary.

The above two definitions allow us to reduce the analysis to the case of servers with a single input and a single output and then to use the results of Chapters 5 and 6. The aggregate server gives a global description of the server, i.e. it models the amount of data that can be served independently of the flows. On the contrary, a residual server only focuses on one flow and on that amount of data used for that flow.

The next two definitions are the counterpart of the service curve definition to the aggregate and residual servers.

DEFINITION 7.5 (Aggregate service curve).– A MIMO server S offers an aggregate service curve β of type if and only if its aggregate server S_∑ offers a service curve β of type .

DEFINITION 7.6 (Residual service curve).– A MIMO server S offers a residual service curve β of type to flow i if and only if its residual server S_i offers a minimal service curve β of type .

In these definitions, the types and of the service curves refer to any definition of a service curve defined in Chapter 5, such as min-plus, strict, maximal and shaper. The notions of aggregate and residual service curves are illustrated in Figure 7.2.

In the case of a strict service curve, the service curve definition depends on the backlogged period and the following lemma might be useful.

LEMMA 7.1 (MIMO and backlogged period).– Let S be an n-server, and . Let A and D be the aggregate arrival and departure processes, respectively. We have the following properties:

• – (s, t] is a backlogged period for ;
• – if (s, t] is a backlogged period for flow i, then it is also a backlogged period for the aggregate server;
• – for all , set s = Start _A,D (t); for all .

PROOF.– Recall that (s, t] is a backlogged period for (A, D) if and only if , and that .

The three statements are then a direct consequence of the equivalence A(t) = , which is true since A_i ≥ D_i for all i.

□

In fact, the residual service offered to a flow depends on the characteristics of the other flows and the scheduling policy of the server. The following sections are devoted to the computation of residual service curves depending on these parameters.

Different number of inputs and outputs: in this chapter, we will only focus on servers in which the number of inputs and outputs is the same and the data that arrived as flow i depart as flow i. It is possible to generalize this framework and to define MIMO servers in which the number of inputs and outputs differ. Chang has defined matrix extensions in [CHA 98], where each departure process in a (min,plus) combination of the arrival processes (the matrix operations are the minimum and the (min,plus) convolution). It should be possible to extend this matrix extension to the case where the number of inputs and outputs differ.

Without being so general, we can restrict to multicast, and in that case, it is possible to model it at no cost by duplicating the processes: for a server with one input and two outputs, for example, we will simply consider it as one server S, and for (A, D) ∈ S, we will define the two outputs as D₁ = D and D₂ = D.

7.2. Blind or arbitrary multiplexing

We say that the multiplexing is blind or arbitrary if no information about the service policy is available. In other words, every service policy needs to be taken into account, and thus the results hold for any service policy.

In this section, we will first show the fundamental result (Theorem 7.1) that enables us to compute the residual min-plus service curves from a server guaranteeing a strict aggregate service curve. In the rest of this section, we will precisely comment on the results, and in particular, the hypothesis made concerning the type of service curves and how to improve the result.

More precisely, in section 7.2.2, we will show that it is possible to compute strict residual service curves, where more knowledge in acquired about the server (maximum service curve or shaper), or at the cost of computing smaller residual service curves (which leads to worse performances). In section 7.2.3, we show that computing a useful min-plus service curve is not possible. The goal of this section is therefore to warn the reader against using service curves with negative values.

7.2.1. Blind multiplexing from an aggregate strict service

We now state the fundamental result of this section: we show how to compute a residual service curve for a flow crossing a server. This result does not depend on the service policy: it is a minimal guarantee. In the following section, more precise results, depending on the service policy, will be given.

THEOREM 7.1 (Blind multiplexing from a strict service curve).– Let S be an n-server offering a strict service curve . If each cumulative arrival process A_i, i ∈ {1,…, n} has an arrival curve α_i, then the residual server for flow i offers a minimal min-plus service curve β_i,

[7.3]

Here, we have to be careful of the hypothesis about the type of service curves. We will illustrate after the proof that they are necessary.

PROOF.– With the notations of the statement, set , the start of the backlogged period (defined in equation [5.10]) and some u ∈ (s, t]. From Proposition 5.5, (s, u] is also a backlogged period, so by definition of the strict service curve, . As s is the start of a backlogged period for the aggregate flow, from Lemma 7.1, , A_i(s) = D_i(s), and we can write

where we used D_j (u) ≤ A_j (u) in the second line. Since the D_j’s are non-decreasing,,

As we assumed that β (0) = 0, and α_j (0) ≥ 0, the inequality also holds for u = s. Then, substituting u − s by v leads to

To conclude, with the definition of β_i in the statement, .

□

Let us now comment on the hypothesis and tightness of this result.

Tightness. We note that if A_i = α_i and the service offered is exactly β(t) in the first backlogged period starting at time 0, then the inequalities in the proof become equalities. The cumulative process is exactly β_j in the first backlogged period, and the result can be considered as tight.

Strict service curve assumption. The result does not hold when the service offered to the aggregate server is a min-plus service curve. For example, consider a 2-server offering the min-plus service curve β_2,2, A₁ = λ₁ and . Assume D = (A₁+ A₂) ∗ β_2,2, as depicted in Figure 7.3. Note that D ≥ A₁, so the departure process for flow 1 can be chosen as D₁ = D. Then, D₂ = D − D₁ = 0. However, β_1,5, which is obviously not a service curve for flow 2. In this example, the priority is given to flow 1. As flow 1 always has some data arriving, these data are served and no service is available for flow 2. The key argument in this example is that the backlogged period is infinite. Another example can be found in [LEB 01, S. 6.2] and [BOU 11a, Proof of Thm. 2].

Nevertheless, this theorem does not state the impossibility of computing residual service curves from a min-plus service curve. In fact, one could have computed a min-plus residual service curve, but it might have taken negative values, which prevents its application for computing performances. This will be the object of Theorem 7.2. More interestingly, it will be possible for the FIFO service policies in section 7.3.1.

Min-plus residual service curve. The computed residual service curve is not a strict service curve. Consider, for instance, a 2-server which serves data at a constant rate 2: it has β = λ₂ as a strict service curve. Let two flows cross this server with respective cumulative arrival processes A₁ (t) = t+ 1 and A₂ (t) = t. An arrival curve of flow 2 is α₂ (t) = t. Figure 7.4 shows the trajectory of the system for the following policy: first, for 0 ≤ t ≤1, flow 1 is given top priority, then for t > 1, flow 2 is given top priority. Since the sum A₁(t) + A₂(t) = 2t + 1, the server is always backlogged and the sum of the cumulative departure functions is D₁(t) + D₂(t) = 2t. It can be checked that is a service curve for flow 1 , but it is not a strict service curve: during the period 1 ≤ t ≤ 2, flow 1 has some data backlogged in the server, but these data are not served at all.

This counter-example also does not state that it is impossible to obtain a strict residual service: Corollary 7.1 will give a strict residual service curve, but it will not be tight. Also, several service policies, such as static priorities, general processor sharing or earliest deadline first, and tight residual strict service curves will be computed in the following section.

7.2.2. Blind multiplexing and strict residual service curves

THEOREM 7.2 (Strict residual service curve).– Let S be an n-server offering a strict service curve . Suppose that the aggregate departure process of flows 2,…,n is constrained by the arrival curve α. Then, the residual server for flow 1 offers a strict service curve .

PROOF.– The proof is similar to the one of Theorem 7.1, and even simpler: let (s, t] be a backlogged period of the aggregate server, for all u ∈ (s, t], we have

so, similarly to the proof of Theorem 7.1,

This holds for any s and t in the same backlogged period, so β₁ is a strict service curve for flow 1.

□

This theorem can be applied in several cases. First, it can be combined with the results of Theorem 5.3. It suffices to compute the arrival curve of the appropriate departure processes. Suppose that α_i is an arrival curve for the arrival process A_i.

For example:

• – if the aggregate server is a σ-shaper, then σ is an arrival curve for the aggregate departure process, and thus, applying Proposition 7.2, it is for the aggregation of flows 2,…, n;
• – if a min-plus service curve is known for each flow j (e.g. by applying Theorem 7.1), then is an arrival curve for the departure process of the aggregation of flows 2,…, n;
• – it is also possible to apply Theorem 7.1 to flow 1 and the aggregation of flows 2,….,n. Then, is a min-plus service curve for the aggregation of flows 2,….,n, and is an arrival curve for the departure process of flows 2,…,n.

Combining the properties of Proposition 5.2 and all of these solutions leads to a strict service curve for flow 1

In particular, we can apply this reasoning to obtain a strict service curve under the same hypothesis as in Theorem 7.1.

COROLLARY 7.1.– Let S be an n-server offering a strict service curve β. If each cumulative arrival process A_i, i ∈ {1,…,n} has an arrival curve α_i, then the residual server for flow i offers a strict service curve

[7.4]

The above computation is quite general and might be used for different purposes. It can be seen as quite technical and with no practical interest, since the residual service curve will, in many cases, be smaller than the min-plus service curve computed in Theorem 7.1 and, in particular, will not lead to better performance bounds.

It can also be applied in two cases:

• – Hierarchical scheduling: a residual service curve is computed for a flow, and this flow might be decomposed into sub-flows. It might be mandatory (depending on the scheduling policy) that the residual service curve that is computed is strict.
• – Improving a strict residual service curve: we will show in the following that for some scheduling policies, it is possible to compute strict residual service curves β₁. If is the service curve computed by Theorem 7.2, then is also a strict service curve. It is especially the case when a σ-shaper is known. In this case, it is also possible to apply this theorem iteratively, by replacing β₁ by and applying Theorem 7.2 again.

7.2.3. Blind multiplexing and aggregate min-plus service curve

Theorem 7.1 derives a min-plus residual service curve from a strict aggregate service curve and we gave some illustrations as to why the strict and min-plus hypotheses are necessary. In this section, we attempt to find a min-plus residual service from a min-plus aggregate service.

WARNING.– This only has a theoretical interest, and we want to warn the reader against using it in practice, as the result cannot be applied to compute performance bounds.

THEOREM 7.3 (Blind multiplexing from a min-plus service curve).– Let S be an n-server offering a left-continuous min-plus service curve β. If each cumulative arrival process has an arrival curve α_i, then the residual server for flow i offers a min-plus service curve ,

[7.5]

PROOF.– Let . The server offers a min-plus service curve, so . From Proposition 3.10, since β is left-continuous, there exists s ∈ [0,t] such that

□

This result does not contradict Theorem 7.1. The key point is that the residual curve may take negative values, and, as it has been discussed in section 5.2.1, Theorem 5.2 does not hold in such a case. The property holds, but D_i (t) may remain null for all values of t, since may remain negative.

Consider the same example as in Figure 7.3. We have A₁ = λ₁ and the service curve β_2,2, so the residual service curve for flow 2 can be computed as , which is shown in Figure 7.5. The theorem ensures that . However, as , no guarantee on the service is in fact computed.

7.3. Some service policies

In this section, we study the most useful service policies:

• – the first-in-first-out (FIFO) policy, where data are served in their order of arrival, which is presented in section 7.3.1;
• – the static priority (SP), where flows are given different levels of priority and the flows with higher priorities are served first, which is presented in section 7.3.2;
• – the general processor sharing (GPS), where the service available is shared in a configurable and fair way among the flows, which is presented in section 7.3.3;
• – the earliest-deadline-first (EDF) policy, where each bit of data is given a deadline, and data are served in an increasing order of the deadlines, which is presented in section 7.3.4.

Before dealing with these different policies, let us give the two key points for the proofs that are similar in the four cases mentioned above.

• – The aggregate service equation: the aggregate server has a service curve (min-plus or strict), which gives the relation between A and D the respective aggregate arrival and departure process, in a way similar to Theorem 7.1.
• – The scheduling fundamental equation: the arrival and departure processes of each flow are related by some equations that depend on the service policy. These equations have to be clearly stated when defining the service policies.

Those two elements are then combined in order to obtain residual service curves.

7.3.1. First-in-first-out

The FIFO policy is one of the most famous service policies that is easy to implement in a per-packet server. Basically, a packet is served after every packet that arrive before it, but before every packet that arrive after it. In the context of network calculus, the FIFO policy needs to be defined in the general context of the cumulative arrival and departure functions of the server, i.e. without mentioning packets.

In this section, we will first give a formal definition of the FIFO policy and then demonstrate how to derive residual service curves of a FIFO server.

We note that, despite its quite intuitive semantics, the formal definition of the FIFO policy is not so straightforward (Definition 7.7) because of the potential discontinuities of the cumulative processes. We will give two kinds of residual service curves in Theorems 7.4 and 7.5. The first is based on the maximal delay and the second type will be more precise. The section ends with a discussion about the state of the art of this policy.

7.3.1.1. FIFO service policy with cumulative processes

Consider the example of a 2-server, with two cumulative arrival processes A₁ and A₂. Their respective departure processes D₁ and D₂ can be computed as illustrated in Figure 7.6.

• – FIFO multiplexing of several cumulative arrival functions: the aggregate cumulative function is A = A₁ + A₂;
• – Input-output transformation D ≥ A ∗ β;
• – FIFO demultiplexing of flows at the exit of the server, compute D₁ and D₂, exploiting the FIFO property of the server.

In the simple case of continuous cumulative arrival processes A₁ and A₂, we denote by D₁ and D₂ their respective departure processes and set A = A₁ + A₂ and D = D₁ + D₂. With the informal definition given above, it is easy to see that for all t ≥ 0, there exists u ≤ t such that A(u) = D(t) (β is continuous) and that . If there are some discontinuities, this has to be adapted as in the next definition, because such a u may not exist.

DEFINITION 7.7 (FIFO service policy).– Let be an n-server. It is a FIFO server (or a FIFO n-server) if,

[7.6]

[7.7]

These equations model the fact that if data of flow i arrived at time t are gone at time , the same is true for any other flow and conversely.

The order of service of data that arrived simultaneously is not defined by Definition 7.7, so we might consider it as arbitrary.

The next lemma characterizes the FIFO policy as a function of the aggregate process, which will help in computing the residual service curves.

LEMMA 7.2 (Aggregation of FIFO flows).– Let be a FIFO n-server. For all , set . Then,,

PROOF.– The two implications from the right-hand side to the left-hand side are direct consequences of the definitions of A and D.

For the two other implications, we proceed by contraposition. Let i ∈ {1,…, n} and suppose that . Then, from Definition 7.7, for all j ≠ i, D_j (t) ≤ A_j (u) and consequently D(t) < A(u), hence the first implication.

The second is similar: suppose that . Then, for all j ≠ i, D_j (t) ≥ A_j (u) and D(t) > A(u).

□

7.3.1.2. Delay bound for the FIFO policy

From the properties shown above, let us now compute the worst-case delay of a flow crossing a server. It is quite intuitive that it should be the same delay as the worst-case delay of the aggregate flow. Indeed, we assume a FIFO-per-flow policy; the delay defined for one flow is the maximum delay of any bit of data when served in their arrival order. This property is maintained for FIFO servers on the aggregate flow. Here, we give a formal proof of this fact.

THEOREM 7.4 (FIFO delay).– Let be a FIFO n-server offering a min-plus service curve . Suppose that for all i ∈ {1,…, n}, is an arrival curve for each flow i. Then, S offers the residual service curve to each flow i and is an upper bound on the delay of the flow i.

Moreover, if and are sub-additive, there exists A₁,…,A_n respecting the constraints such that is the worst-case delay for flow i.

PROOF.– For , set and .

From Corollary 6.1, is a service curve for the aggregate server: D ≥ A ∗ and . From Lemma 7.2, this implies that for all . Thus,

Under the additional hypotheses and from Theorem 5.2, there exists (A₁,A₂, …, A_n, D₁, D₂,…, D_n) ∈ S such that there exists t with . Indeed, it suffices to take A_i = α_i (as α_i is sub-additive) and 0). Finally, the two equivalences of Lemma 7.2 lead to , which terminates the proof.

□

7.3.1.3. Residual service curves for a FIFO server

The maximum delay of a flow crossing a server is simple to compute: it is the delay of the aggregate flow. Dealing with residual service curves is much more involving. Indeed, an infinite family of residual service curves can be found, that cannot be compared. But, in contrast to the case of blind multiplexing, we do not need to consider strict service curves: min-plus service curves are enough.

THEOREM 7.5 (FIFO residual service curve).– Let be a FIFO n-server offering a min-plus service curve . Suppose that for all i ∈{1,…,n}, α_i ∈ is an arrival curve for flow i. Then, is a min-plus service curve for flow i with

The existence of an arbitrary θ parameter is intriguing at first, but an interpretation will be given in section 7.3.1.4.

PROOF.– Let .

Fix and define . Informally, u is the arrival time of the data that depart at time t, and because of the left-continuity of A and D, . But, from Lemma 7.2, it holds that ,

Now, fix . Intuitively, we differentiate two cases: if the arrival time u is before or after t − θ. If u < t − θ, because of the FIFO hypothesis, no data that exit before time t arrived after time t − θ. If u ≥ t − θ, we cannot say anything concerning the arrivals after t − θ.

In the latter case, . This means that .

In the first case, Proposition 3.10 together with the left-continuity of β and A implies that there exists such that and , necessarily , we also have for all flow j. Then,

As we also have , we obtain . This finishes the proof.

□

This theorem does not improve the worst-case delay that has already been computed in Theorem 7.4. However, Theorem 7.5 is much more precise as it computes residual service curves. First, better arrival curves for the output flows can be computed. Second, computing service curves can improve the performance bounds when dealing with a network of servers, as stated in section 6.1.2. This will be more precisely discussed in section 7.3.1.4.

EXAMPLE 7.1.– Consider a FIFO server crossed by two flows. Suppose that is an arrival curve for flow 2 and that is a service curve for the server, with R >r. Let us compute the residual service curves for flow 1 using Theorem 7.5.

If , then . In this case, the curves can be compared and the greatest is with .

If , then . This function is represented in Figure 7.7. This figure also illustrates the fact that those curves cannot be compared.

COROLLARY 7.2 (Arrival curve of the departure function of a FIFO server).– Let be a FIFO n-server offering a min-plus service curve . Suppose that for all is an arrival curve for each arrival flow i. With defined as in Theorem 7.5, an arrival curve for the cumulative departure process of flow i is

[7.8]

PROOF.– From Theorem 5.3, for each is an arrival curve for the departure process of flow i. Then, from Proposition 5.2, the infimum of arrival curves for a cumulative process is still an arrival curve for this process, hence the result.

□

EXAMPLE 7.2.– Continuing Example 7.1, assume that the arrival curve for flow 1 is and that . For all . Arrival curves can be compared and the smallest is for . The departure process has then arrival curve

7.3.1.4. Discussing FIFO results

The FIFO service policy is a very special case in network calculus theory. Indeed, since the service inside each flow is also FIFO, the aggregate flow is also served in a FIFO way, so the analysis can be done using the results of Chapter 5, and in particular, Theorem 5.2 can be applied, which leads to Theorem 7.4. We also showed the optimality of this theorem in the sense that the computed delay bound cannot be improved by the more complex Theorem 7.5.

Using this latter theorem allows us to analyze a FIFO server per-flow and compute a residual service curve. The surprising fact here is that an infinite family of service curves, parametrized by θ , is then computed, and that these service curves are not comparable.

The θ parameter is a bet on the waiting time d of flow i. If the waiting time is less than θ , then β^θ does not give any information about the service offered to the flow (β^θ (d) = 0). However, if the waiting time is greater than θ, it means that the server has begun to send some data of others flows. With the notations of Example 7.1, the discontinuity of the service curve represents the amount of data that can be reserved for data that spent more than a duration θ in the server for flow 1.

The parameter θ is important when analyzing a sequence of FIFO servers. It will be detailed in one example in Chapter 10, but roughly speaking, one parameter θ_j is computed for each server j, and from these parameters, the performance bounds can be computed. Choosing adequate θ_j parameters to get the smallest delay bound is the core of the works of [LEN 04] and [BIS 10].

We note that the delays of the FIFO policy on a full topology can also be analyzed without resorting to Theorem 7.5 but by using linear programming, as in Chapter 11.

Finally, the arrival curve of the departure process computed with Corollary 7.2 is more accurate than considering only the global delay [BOY 08]. Some analytic expressions have been developed for some sub-classes of functions. In [LEB 01, Thm. 6.2.2], the authors consider a minimal rate-latency service curve , any sub-additive function α₂ and and prove that , with an analytic expression of . This result is generalized by [CHO 02], where Theorem 7.5 is not used; instead, the authors consider a λ_R-greedy shaper, and that α₁ and α₂ are both piecewise linear concave; they give a tight characterization of an arrival curve of the departure process and an analytic expression if . Conversely, in [BOY 08], the author considers α₁ as any piecewise linear concave function and and gives an analytic expression for .

7.3.2. Static priority

Consider a server crossed by two flows. Suppose that flow 2 has a higher priority than flow 1. At first sight, one could say that this is the worst service policy for flow 1 and that the only residual service curve that can be computed is the one from Theorem 7.1. This is not completely true, as when the service policy is known, we can ensure that the residual service curves that are computed are strict.

DEFINITION 7.8 (Preemptive static priority (SP)).– Let be an n-server crossed by flows 1,…,n and < be a total order on {1,…, n}. This server is a (preemptive) SP n-server with priority order < if ,

In other words, if some data with higher priority than flow i are backlogged, then flow i is not served. With our convention, if i < j, then flow i has a higher priority than flow j. From the definition, it is natural to consider strict service curves.

THEOREM 7.6 (Residual service curve for SP).– Let S be a preemptive SP n-server taking the natural order as priority order, offering an aggregate strict service curve β. Suppose that for all is an arrival curve for each arrival flow i. Then, β_i is a strict service curve offered to flow i, with

PROOF.– From the definition, the flows with lower priority than flow i have no influence on the service offered to flow i, and only the aggregation of flows with higher priority matters. Therefore, it is sufficient to consider a server crossed by two flows: the flow of interest, which we now rename flow 2, and the aggregate flow of flows j, j <i, that has an arrival curve , which we rename flow 1.

Let u and v with u < v, be two times in the same backlogged period for flow 2 in the server. From Lemma 7.1, u and v are in the same backlogged period of the aggregate flow, and we have .

Let p be the start of the backlogged period of u for flow 1. From the definition, no data can be served for flow 2 between p and u, and we have:

Between times p and v, we also have . As , we obtain

We can apply the above formula for every , as w remains in the same backlogged period as v:

As D₂ is non-decreasing, we also have and

[7.9]

[7.10]

[7.11]

As , we have

Moreover, as D₂ is non-decreasing,

□

This result considers that the scheduler is preemptive: if some data of a high priority flow arrives in the server, then is it served even if some data of a low priority flow were being served. Non-preemptive policies are often used when flows are made of packets. This will be studied in Chapter 8 and residual service curves will be computed in Theorem 8.3.

7.3.3. General processor sharing

General processor sharing (GPS) is a policy that guarantees a proportion of the global service to each flow. When some flow has no data in the server, then its remaining service is shared among the other flows.

DEFINITION 7.9 (GPS).– Let S be an n-server. This server is a GPS server (or GPS n-server) with parameters , for all i, for all interval (s, t] such that flow i is backlogged, and for all j,

[7.12]

With the same notations as in the definition, we say that is the parameter of flow i, and flow i is guaranteed a proportion of the service. If for all flows i, then the multiplexing is blind: there is no knowledge about the service policy. If flows exist (but not all) with null parameters, then those flows are given the lowest priority compared to flows with positive parameters. As a result, in the following, we will only consider flows with positive parameters.

The guarantee on the service depends on the difference . Therefore, it is natural to consider strict service curves.

THEOREM 7.7 (GPS residual service curve).– Let S be a GPS n-server offering a strict service curve β , with non-null parameters . Then, is a strict service curve offered to flow i, where

[7.13]

PROOF.– Consider flow i, and s ≤ t in the same backlogged period for flow i. Then, s and t are in the same backlogged period of the aggregate flow and . On the other hand, we have . Summing those terms leads to

So

□

Theorem 7.7 gives a residual service curve regardless of the intensity of the crosstraffic. It allows us to get some bounds independent of the cross-traffic¹, but these bounds can be very loose and can even be infinite although the server is stable. For example, consider two flows with respective arrival curves crossing a server with service curve . Suppose that and . Then, Theorem 7.7 guarantees a strict service curve to flow 2. As α₂ > , stability is not ensured. However, from Theorem 7.1, the service curve is a min-plus service curve that is guaranteed for flow 2: this guarantee is ensured regardless of the service policy. We now show that this service curve can be used to improve the one of Theorem 7.7 under some additional assumptions.

THEOREM 7.8.– Consider a GPS n-server with positive parameters offering a strict service curve β. Suppose that each flow i is α_i-upper constrained. If β is convex and there exists such that is concave, then a strict service curve for flow n is

Note that in the proof, we will use variable capacity nodes curves. It will be shown in Chapter 9 that strict and variable capacity node service curves are equivalent in the class of functions that we consider (convex, with a finite asymptotic service rate).

Informally, a variable capacity node (vnc) is a server for which a function C can be defined in such a way that C(t) is the amount of service that has been offered to data up to time t. Then, if (s, t] is a backlogged period, the amount of data served between time s and t is exactly C(t) − C(t). If (s, t] is not a backlogged period, the amount of data served is less than C(t) − C(s): some available service is when the server is empty. A server has a vnc service curve β if C(t) − C(s) ≥ β(t − s) for all s ≤ t.

Before proving this theorem, let us state some preliminary lemmas. First, we can generalize the definition of GPS to a subset of flows J ⊆ {1,…,n}.

LEMMA 7.3.– Suppose that flows 1,…,n cross S a GPS n-server with parameters and suppose that β_J is a strict service curve for the aggregation of flows i ∈ J ⊆{1,…n}. Then, the curve is a strict service curve for flow i, i ∈ J.

PROOF.– Let s < t such that (s, t] is a backlogged period of flow i. Then,

□

We will use the property that in a variable capacity node with service curve β, there exists a non-decreasing function C such that for s and t in the same backlogged period, D(t) — D(s) = C(t) — C(s) ≥ β(t − s).

Set . Define .

LEMMA 7.4.– Under the same hypothesis as in Theorem 7.8, is a strict service curve for the aggregation of flows 2,…,n.

PROOF.– In this proof, in order to avoid too many normalizations, we assume that . This is done without loss of generality, as the final result only depends on the ratios between parameters.

Let (s, t] be a backlogged period for the aggregation of flows 2,…,n. It is also a backlogged period for the total aggregate flow including flow 1. Let us denote and . Then, we have

and

Let p be the start of the backlogged period at s for flow 1. In the interval of time (p, s], the service offered to flow 1 is then at least and D₁(p) = A₁(p):

Combining the last two equations gives

which can be rewritten as

and using the arrival and service curves (and D₁(t) ≤ A₁(t))

As β is convex and non-negative and non-decreasing and α₁ concave, is convex and non-decreasing from time t₁.

Suppose that t − s ≥ t₁. As p ≤ s by definition, t − p ≥ t − s and . Then

When t – s ≤ t₁, as the D_is are non-decreasing, , which ends the proof.

□

Now, we can derive a new service curve for each flow 2,…,n.

LEMMA 7.5.– Under the same hypothesis as in Theorem 7.8, for each i ≥ 2,

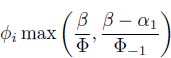
is a strict service curve for flow i.

PROOF.– From Theorem 7.7 and Lemma 7.3, and are strict service curves for flow i. Then, the maximum of the two curves is also a strict service curve for flow i.

It remains to show that if This is the case since if t ≤ t₁, then and .

□

We can now prove Theorem 7.8.

PROOF OF THEOREM 7.8.– The result is proved by induction and by combining Lemmas 7.3 and 7.4. Define (so that and ) and and

We will prove that for all is a strict service curve for the aggregation of flows i, …,n.

This is true for i = 1 by Theorem 7.7. Suppose it is true for i < n. Then is a strict service curve for flows i, . . . , n. Again, by Lemma 7.4, is a strict service curve for flows i + 1, . . . , n. But, as t_i ≥ t_i+1 by construction,

As a result, . It remains to check that for all . The reasoning is exactly the same as in the proof of Lemma 7.5.

□

The service curve computed in Theorem 7.8 can be optimized by setting a specific numbering for the flows. This ordering always consists in taking the flow minimizing t_i. If we assume that (which ensures that the backlogged periods are finite) for some t, all the t_is are then finite: indeed, otherwise, one would have , which is in contradiction with the hypothesis. Taking this order for the flows is optimal. Indeed, take A_i = α_i for all flow i and C(t) = β(t) (satisfying the convexity and concavity assumptions). At time t₁ , flow 1 is not backlogged anymore, while the other flows are backlogged. The service offered from time t₁ is exactly β(t) − α₁(t), and this service divides into the other flows and so on.

We note that the convexity and concavity hypothesis have only been used for ensuring that is positive and non-decreasing from t₁. The result could be applied in a more general setting by taking the non-decreasing envelope of (and recursively for each flow).

Consider the same example as earlier: and and , . We can compute t₁ = 0.5, and the residual strict service curve for flow 2 is . The construction is illustrated in Figure 7.8.

As mentioned in [PAR 93], GPS is an idealized discipline that assumes that bits of data are infinitely divisible. Practical implementations of GPS will be presented in Chapter 8.

7.3.4. Earliest-deadline-first

The earliest-deadline-first (EDF) service policy has been defined for scheduling tasks on a processor. Each task i has a release time r_i and a deadline d_i, sometimes called the relative deadline. The scheduler always chooses to run the task i with the smallest value r_i + d_i (called the absolute deadline). This is a preemptive scheduling policy: if a task is running, and if a new task is released with the smallest absolute deadline, the scheduler selects this new task, and suspends the current task, which will be resumed once it gets the smallest absolute deadline again.

The EDF policy is widely used and has been proved optimal in [BAR 90, BAR 99], in the context of a constant rate service.

EDF can be generalized as network packet scheduling: with each packet is associated a deadline d_i, and an arrival time r_i; the scheduler then always selects the packet with the smallest value r_i + d_i. In the case of the equality of absolute deadline, no priority is defined. This generalization is mainly theoretical, since preemption is very rare in networks.

There are few works on EDF in the network calculus framework. These works are mainly stated in the context of constant rate servers. Some recent works [LIE 11] present EDF as a generalization of FIFO and static priority and introduce the notion of Δ-scheduler. In this section, we present the results of the literature in the more general context of strict service curves and discuss the results of [LIE 11] in section 7.3.4.3. The scheduling problem has also been discussed in [LIE 96], and scheduling algorithms following EDF have been defined in [SAR 99].

7.3.4.1. EDF modeling

The definition of the EDF service policy as a formal relation on cumulative functions is not as straightforward as the previous service policies. For A, a cumulative arrival process, let us introduce the notations and , the respective processes before and after T. It can be easily checked that . We also denote by the departure process corresponding to the arrival process (we take into account departures that correspond to data arrived after T). More formally, and .

In our model, we associate a deadline d_i with each flow i (each bit of data of flow i has the same relative deadline d_i) and define .

Figure 7.9 illustrates the behavior of the EDF policy: consider flows i and j and time T. Data in all have an absolute deadline before T, whereas data in all have a deadline after T. As a result, has a higher priority than .

DEFINITION 7.10 (EDF scheduler).– An n-server S is an EDF server (or EDF n-server) with deadline parameters , has a higher priority than . Equivalently (replacing T by , we can write that has a higher priority than .

The aim of the next theorem is to compute the residual service curve for a given flow i. For this flow i, and a given time t, we can define

the start of the backlogged period at time t of the flows with deadline before , i.e. flows . We then have

• – ;
• – for all ;
• – no data from flows with lower priority than flows are served between times and , with . Indeed, either a higher-priority flow is backlogged (between times and t) or flow is backlogged (between times t and ).

With these remarks, it is now possible to compute residual service curves under the EDF policy. Similar to the FIFO case, we will compute an infinite family of residual service curves, indexed by a parameter θ.

THEOREM 7.9 (EDF residual service curve).– Let be an EDF n-server offering a strict service curve β ∈ C. Suppose that each flow i ∈ {1,…,n} has a deadline d_i and is constrained by the arrival curve . Then, is a min-plus service curve for flow i with

PROOF.– Let , set and .

Fix and . Let .

As in the proof of Theorem 7.5, we distinguish two cases, whether or . We also note that u is in the same backlogged period as t for flow i.

If , then, .

If , then , so:

1) ;

2) and t are in the same backlogged period for flow i, no data from the lower-priority flows are served so between times and .

We can proceed as in Theorem 7.6 where the cross-traffic is composed of flows :

The second line uses and , the third line uses that is an arrival curve for and the last inequality uses that . Finally, as , we can write

Finally, as min, then and a min-plus service curve for flow i is .

□

7.3.4.2. Deadline compatibility and optimality of EDF

If every flow is assigned a (relative) deadline, then a service policy is deadline compatible if the delays of those flows never exceed their deadline.

DEFINITION 7.11 (Deadline compatibility).– An n-server S is said to be deadline compatible with parameters and under constraints if for all such that for all i, A_i is α_i-constrained and

[7.14]

Remember that from Proposition 3.2, for all . A necessary condition for deadline compatibility is valid for any service policy.

THEOREM 7.10 (Necessary condition for deadline compatibility).– For all , if an n-server with aggregate service is deadline compatible under constraints , then

[7.15]

PROOF.– Set and choose such that , with and (this is possible since the aggregate server is . If S is deadline compatible, then . Therefore, for all and all and, in particular, with ,

□

This condition is not sufficient, especially because we consider min-plus service curves. Consider a 2-server and that the two flows have respective arrival curves and and deadlines 3 and 5. Assume that the server guarantees a min-plus service curve . Now consider the arrival processes and two units of data arrive at time 0 for flow 2 and at time 0.5 for flow 1. If the departure process is as depicted in Figure 7.10, then data of flow 2 are served by time 0.5 (before the arrival of flow 1, which has a smaller deadline) and those of flow 1 are served by time 4, which means its delay is 3.5 > 3. This example is quite generic, so from now on, we will focus on strict service curves only, where the above condition is necessary and sufficient.

THEOREM 7.11 (Deadline compatibility condition).– For all β ∈ C super-additive, there exists an n-server with aggregate service S_strict(β) that is deadline compatible under sub-additive constraints if and only if

[7.16]

The additional condition is here only to restrict to the maximal length of a backlogged period.

PROOF.– We show that the EDF server is deadline compatible. Set .

On the one hand, set A_i = α_i and choose D₁, …,D_n such that D = β on [0, v). If S is deadline compatible, then for all t ∈ [0, v), . Therefore, one must have

On the other hand, suppose that for all t ∈ [0,v) and consider the EDF policy for this server. For each flow i, set θ = d_i, so . Then, , so the deadline d_i is satisfied.

□

Combining Theorems 7.10 and 7.11 yields EDF optimality with regard to deadline compatibility. Given a strict service curve, if a scheduler respects the given set of deadlines, then its capacity satisfies equation [7.15], and if this condition holds, then the EDF scheduler also respects the deadlines.

This result was already known in the context of scheduling (see [BAR 90]) but only for sporadic tasks and constant rate service.

7.3.4.3. EDF, FIFO, SP and -schedulers

The EDF policy can be seen as a generalization of the FIFO policy in the context of strict service curves. Indeed, if a server guarantees a strict service curve, then it also guarantees a min-plus service curve and Theorem 7.9 still holds. Then, it can be interpreted in the EDF context with for all i and j: when all deadlines are equal and an EDF scheduler behaves as a FIFO scheduler.

The EDF policy can also be interpreted as a generalization of the static priority policy, if we allow infinite values for if , d_i can be interpreted as infinitely larger than d_j, then flow j will have the priority over flow i and . On the contrary, if , flow i will have the priority over flow j and . The residual curve computed for is , where is the set of flows with higher priority than flow i.

These remarks and the results about the EDF residual service curve we presented come from [LIE 11], where the proof is done for constant rate servers under the name of Δ-schedulers. The proof we gave here is a corrected and direct adaptation to the strict service curve case.

7.4. Summary

The results of this chapter are recapitulated in the following figure and table. For the sake of simplicity, we write the formulas for two flows.