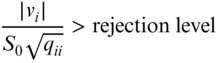CHAPTER 21
BLUNDER DETECTION IN HORIZONTAL NETWORKS
21.1 INTRODUCTION
Up to this point, data sets were assumed to be free of blunders. However, when adjusting real observations, the data sets are seldom blunder free. Not all blunders are large, but no matter their sizes, it is desirable to remove them from the data set. In this chapter, methods used to detect blunders before and after an adjustment are discussed.
Many examples can be cited that illustrate mishaps that have resulted from undetected blunders in survey data. However, few could have been more costly and embarrassing than a blunder of about 1 mile that occurred in an early nineteenth-century survey of the border between the United States and Canada near the north end of Lake Champlain. Following the survey, construction of a US military fort was begun. The project was abandoned two years later when the blunder was detected, and a resurvey showed that the fort was actually located on Canadian soil. The abandoned facility was subsequently named “Fort Blunder!”
As discussed in previous chapters, observations are normally distributed. This means that occasionally, large random errors will occur. However, in accordance with theory, this seldom happens. Thus, large errors in data sets are more likely to be blunders than random errors. Common blunders in data sets include number transposition, entry and recording errors, station misidentifications, and others. When blunders are present in a data set, a least squares adjustment may not be possible or will, at a minimum, produce poor or invalid results. To be safe, the results of an adjustment should never be accepted without an analysis of the post-adjustment statistics.
21.2 A PRIORI METHODS FOR DETECTING BLUNDERS IN OBSERVATIONS
![]() In performing adjustments, it should always be assumed that there are possible observational blunders in the data. Thus, appropriate methods should be used to isolate and remove them. It is especially important to eliminate large blunders prior to the adjustment of nonlinear equations, since blunders can cause the solution to diverge. In this section, several methods are discussed that can be used to isolate blunders in a horizontal adjustment.
In performing adjustments, it should always be assumed that there are possible observational blunders in the data. Thus, appropriate methods should be used to isolate and remove them. It is especially important to eliminate large blunders prior to the adjustment of nonlinear equations, since blunders can cause the solution to diverge. In this section, several methods are discussed that can be used to isolate blunders in a horizontal adjustment.
21.2.1 Use of the K Matrix
In horizontal surveys, the easiest method available for detecting blunders is to use the redundant observations. When the approximate station coordinates are computed using standard surveying methods, they should be close to their final adjusted values. Thus, the difference between observations computed from the approximate coordinates and their observed values (K matrix) are expected to be small in size. If an observational blunder is present, there are two possible situations that can occur with regard to the K-matrix values. If the observation containing a blunder is not used to compute initial coordinates, its corresponding K-matrix value will be relatively large. However, if an observation with a blunder is used in the computation of the initial station coordinates, the remaining redundant observations to that station will have relatively large values.
Figure 21.1 shows the two possible situations. In Figure 21.1(a), a distance blunder is present in line BP and is shown by the length PP′. However, this distance was not used in computing the coordinates of station P and thus, the K-matrix value for BP′ − BP0 will suggest the presence of a blunder by its relatively large size. In Figure 21.1(b), the distance blunder in BP was used to compute the initial coordinates of station P′. In this case, the redundant angle and distance observations connecting P with A, C, and D will show large discrepancies in the K matrix. In the latter case, it is possible that some redundant observations may agree reasonably with their computed values, since a shift in a station's position can occur along a sight line for an angle, or along a radius for a distance. Still most redundant observations will have large K-matrix values, and thus raise suspicions that a blunder exists in one of the observations used to compute the coordinates of station P.

FIGURE 21.1 Presence of distance blunder in computations.
21.2.2 Traverse Closure Checks
As mentioned in Chapter 8, errors can be propagated throughout a traverse to determine the anticipated closure error. Large complex networks can be broken into smaller link and loop traverses to check estimated closure errors against their actual values. When a loop fails to meet its estimated closure, the observations included in the computations should be checked for blunders.
Figure 21.2(a) and (b) shows a graphical technique to isolate a traverse distance blunder and angular blunder, respectively. In Figure 21.2(a), a blunder in distance CD is shown. Notice that the remaining courses, DE and EA, are translated by the blunder in the direction of course CD. Thus, the length of closure line (A′A) will be nearly equal to the length of the blunder in CD with a direction that is consistent with the azimuth of CD. Since other observations contain small random errors, the length and direction of closure line, A′A, will not match the blunder exactly. However when one blunder is present in a traverse, the misclosure and the blunder will be close in both length and direction.

FIGURE 21.2 Effects of a single blunder on the traverse closure error.
In the traverse of Figure 21.2(b), the effect of an angular blunder at traverse station D is illustrated. As shown, the courses DE, EF, and FA′ will be rotated about station D. Thus, the perpendicular bisector of the closure line AA′ will point to station D. Again, due to random errors in other observations, the perpendicular bisector may not intersect the observation with the blunder precisely, but it should be close enough to identify the angle with the blunder. Since the angle at the initial station is not used in traverse computations, it is possible to isolate a single angular blunder by beginning traverse computations at the station with the suspected blunder. In this case, when the blunder is not used in the computations, estimated misclosure errors will be met and the blunder can be isolated to the single unused angle. Thus, in Figure 21.2(b), if the traverse computations were started at station D and used an assumed azimuth for the course of CD, the traverse misclosure when returning to D would be within estimated tolerance since the angle at D is not used in the traverse computations. Of course this means that the angles should not be adjusted prior to the traverse computations.
21.3 A POSTERIORI BLUNDER DETECTION
When doing a least squares adjustment involving more than the minimum amount of control, both a minimally constrained and overconstrained adjustment should be performed. In a minimally constrained adjustment, the data need to satisfy the appropriate geometric closures and are not influenced by any control errors. After the adjustment, a χ2 test1 can be used to check the a priori value of the reference variance against its a posteriori estimate. However, this test is not a good indicator of the presence of a blunder since it is sensitive to poor relative weighting. Thus, the a posteriori residuals should also be checked for the presence of large discrepancies. If no large discrepancies are present, the observational weights should be altered and the adjustment rerun. Since χ2 test is sensitive to weights, the procedures described in Chapters 7 through 10 should be used for building the stochastic model of the adjustment.
Besides the sizes of the residuals, the signs of the residuals may also indicate a problem in the data. From normal probability theory, residuals are expected to be small and randomly distributed. In Figure 21.3, a small section of a larger network is shown. Notice that the distance residuals between stations A and B are all positive. This is not expected from normally distributed data. Thus, it is possible that either a blunder or systematic error is present in some or all of the survey. If both A and B are control stations, part of the problem could stem from control coordinate discrepancies. This possibility can be isolated by doing a minimally constrained adjustment.

FIGURE 21.3 Distribution of residuals by sign.
Although residual sizes can suggest observational errors, they do not necessarily identify the observations that contain blunders. This is due to the fact that least squares solution generally spreads a large observational error or blunder out from its source radially. However, this condition is not unique to least squares adjustments, since any arbitrary adjustment method, including the compass rule for traverse adjustment, will also spread a single observational error throughout the entire observational set.

FIGURE 21.4 Survey network.
While an abnormally large residual may suggest the presence of a blunder in an observation, this is not always true. One reason for this could be poor relative weighting in the observations. For example, suppose that angle GAH in the Figure 21.4 has a small blunder but has been given a relatively high weight. In this case, the largest residual may well appear in a length between stations G and H, B and H, C and F, and most noticeably between D and E due to their distances from station A. This is because the angular blunder will cause the network to spread or compress. When this happens, the sign of the distance residuals between G and H, B and H, C and F, and D and E may all be the same and thus, may indicate the problem. Again, this situation can be minimized by using proper methods to determine observational variances so they are truly reflective of the estimated errors in the observations.
21.4 DEVELOPMENT OF THE COVARIANCE MATRIX FOR THE RESIDUALS
![]() In Chapter 5 it was shown how a sample data set could be tested at any confidence level to isolate observational residuals that were too large. The concept of statistical blunder detection in surveying was introduced in the mid-1960s and utilizes the cofactor matrix for the residuals. To develop this matrix, the adjustment of a linear problem can be expressed in matrix form as
In Chapter 5 it was shown how a sample data set could be tested at any confidence level to isolate observational residuals that were too large. The concept of statistical blunder detection in surveying was introduced in the mid-1960s and utilizes the cofactor matrix for the residuals. To develop this matrix, the adjustment of a linear problem can be expressed in matrix form as
where C is a constants vector, A is the coefficient matrix, X is the estimated parameter matrix, L is the observation matrix, and V is the residual vector. Equation (21.1) can be rewritten in terms of V as
where T = L − C that has a covariance matrix of W−1 = S2Qll. The solution of Equation (21.2) results in the expression
Letting ε represent a vector of true errors for the observations, Equation (21.1) can be written as
where ![]() is the true value for the unknown parameter X, and thus
is the true value for the unknown parameter X, and thus
Substituting Equations (21.3) and (21.5) into Equation (21.2) yields
Expanding Equation (21.6) results in
Since (ATWA)−1 = A−1W−1A−T, Equation (21.7) can be simplified to
Factoring Wε from Equation (21.8), yields
Recognizing (ATWA)−1 = Qxx and defining Qvv = W−1 − AQxxAT, Equation (21.9) can be rewritten as
where Qvv = W−1 − A Qxx AT = W−1 − Qll.
If we let R be the product of W and Qvv, the R matrix is both singular and idempotent. Being singular, it has no inverse. When a matrix is idempotent, the following properties exist for the matrix: (a) The square of the matrix is equal to the original matrix (i.e., RR = R), (b) every diagonal element is between zero and 1, and (c) the sum of the diagonal elements, known as the trace of the matrix, equals the degrees of freedom in the adjustment. This latter property is expressed mathematically as
(d) The sum of the square of the elements in any single row or column equals the diagonal element. That is,
Now consider the case when all observations have zero errors except for a particular observation li that contains a blunder of size Δli. A vector of the true errors is expressed as

If the original observations are uncorrelated, the specific correction for Δvi can be expressed as
where qii is the ith diagonal of the Qvv matrix, wii is the ith diagonal term of the weight matrix, W, and ri = qii wii is the observation's redundancy number.
When the system has a unique solution, ri will equal zero. If the observation is overconstrained, ri would equal one. The redundancy numbers provide insight into the geometric strength of the adjustment. An adjustment that in general has low redundancy numbers will have observations that lack sufficient checks to isolate blunders, and thus the chance for undetected blunders to exist in the observations is high. Conversely, a high overall redundancy number enables a high level of internal checking of the observations, and thus there is a lower chance of accepting observations that contain blunders. The quotient of r/m is called the relative redundancy of the adjustment where r is the total number of redundant observations in the system and m is the number of observations. As discussed in Section 21.9.1, a well-designed network will have individual observational redundancy numbers that are all close to the relative redundancy number.
21.5 DETECTION OF OUTLIERS IN OBSERVATIONS: DATA SNOOPING
![]() Equation (21.10) defines the covariance matrix for the vector of residuals, vi. From this the standardized residual is computed using the appropriate diagonal element of the Qvv matrix as
Equation (21.10) defines the covariance matrix for the vector of residuals, vi. From this the standardized residual is computed using the appropriate diagonal element of the Qvv matrix as
where ![]() is the standardized residual, vi the computed residual, and qii the diagonal element of the Qvv matrix. Using the Qvv matrix, the standard deviation in the residual is
is the standardized residual, vi the computed residual, and qii the diagonal element of the Qvv matrix. Using the Qvv matrix, the standard deviation in the residual is ![]() . Thus, if the denominator of Equation (21.15) is multiplied by S0, a t statistic is defined. If the residual is significantly different from zero, the observation used to derive the statistic is considered to be a blunder. As suggested by Willem Baarda (1968), the test statistic for this hypothesis test is
. Thus, if the denominator of Equation (21.15) is multiplied by S0, a t statistic is defined. If the residual is significantly different from zero, the observation used to derive the statistic is considered to be a blunder. As suggested by Willem Baarda (1968), the test statistic for this hypothesis test is
Baarda computed rejection criteria for various significance levels (see Table 21.1), determining the α and β levels for the Type I and Type II errors. The interpretation of these criteria is shown in Figure 21.5. When a blunder is present in the data set, the t distribution is shifted, and a statistical test for this shift may be performed. As with any other statistical test, two types of errors can occur. A Type I error occurs when data are rejected that do not contain blunders, and a Type II error occurs when a blunder is not detected in a data set where one is actually present. The rejection criteria are represented by the vertical line in Figure 21.5 and their corresponding significance levels are shown in Table 21.1. In practice, authors2 have reported that a value of 3.29 also works as a criterion for rejection of blunders.
TABLE 21.1 Rejection Criteria with Corresponding Significance Levels
| α | 1 − α | β | 1 − β | Rejection Criteria |
| 0.05 | 0.95 | 0.80 | 0.20 | 2.8 |
| 0.001 | 0.999 | 0.80 | 0.20 | 4.1 |
| 0.001 | 0.999 | 0.999 | 0.001 | 6.6 |

FIGURE 21.5 Effects of a blunder on the t distribution.
Thus, the approach is to use a rejection level given by a t distribution with r − 1 degrees of freedom. The observation with the largest absolute value of ti as given by Equation (21.17) is rejected when it is greater than the rejection level. That is, the observation is rejected when
Since the existence of any blunder in the data set will affect the remaining observations, and since Equation (21.18) is dependent on S0 whose value was computed from data containing blunders, all observations that are detected as blunders should not be removed in a single pass. Instead, only the largest or largest independent group of observations should be deleted. Furthermore, since Equation (21.18) is dependent on S0, it is possible to rewrite the equation so that it can be computed during the final iteration of a nonlinear adjustment. In this case, the appropriate equation is
A summary of procedures for this manner of blunder detection is as follows:
- Step 1: Locate all standardized residuals that meet the rejection criteria of Equation (21.17) or (21.18).
- Step 2: Remove the largest detected blunder or unrelated blunder groups.
- Step 3: Rerun the adjustment.
- Step 4: Continue steps 1 through 3 until all detected blunders are removed.
- Step 5: If more than one observation is removed in steps 1 through 4, reenter the observations in the adjustment in a one-at-a-time fashion. Check the observation after each adjustment to see if it is again detected as a blunder. If it is, remove it from the adjustment or have that observation reobserved.
Again, it should be noted that this form of blunder detection is sensitive to improper relative weighting in observations. Thus, it is important to use weights that are reflective of the observational errors. Proper methods of computing estimated errors in observations, and weighting, were discussed in Chapters 7 through 10.
21.6 DETECTION OF OUTLIERS IN OBSERVATIONS: THE TAU CRITERION
![]() Data snooping is based on Equation (21.16) being a t statistic. However, when a blunder is present in a data set both S0 and Sv are affected by the blunder. Thus, Alan J. Pope (1976) stated that Equation (21.16) is instead a τ (tau) statistic where the critical τ value is computed as
Data snooping is based on Equation (21.16) being a t statistic. However, when a blunder is present in a data set both S0 and Sv are affected by the blunder. Thus, Alan J. Pope (1976) stated that Equation (21.16) is instead a τ (tau) statistic where the critical τ value is computed as
In Equation (21.19), the probability of the computed τ from Equation (21.16) being greater than τα/2 is ![]() , which is referred to as the transformation for control of the Type I error where n is conventionally taken to be the number of nonspur observations in the adjustment. A nonspur observation is any observation where σν and v are nonzero. Recalling Equation (21.16) and using the τ criterion, observations are considered for rejection when
, which is referred to as the transformation for control of the Type I error where n is conventionally taken to be the number of nonspur observations in the adjustment. A nonspur observation is any observation where σν and v are nonzero. Recalling Equation (21.16) and using the τ criterion, observations are considered for rejection when
The procedures for eliminating and removing blunders using the τ statistic are the same as those used in data snooping. That is, the observation with the largest standardized residuals that is detected as an outlier or blunder using Equation (21.20) is removed from the data set and the adjustment rerun. This procedure is continued, removing a single observation at a time until no more observations are detected as outliers or blunders. Again the rejected observations should be reinserted into the adjustment in a one-at-a-time fashion to determine if they are still detected as blunders. Any observations that are detected as a blunder a second time are discarded as blunders or must be reobserved.
Even though data snooping and the τ criterion are theoretically different, they have been shown in practice to yield similar results. Thus, the matter of which method of statistical blunder detection to use is a matter of personal preference. As shown in Figure 21.6, the software ADJUST allows the user to select the blunder detection method of their choice.

FIGURE 21.6 Data set with blunders.
21.7 TECHNIQUES USED IN ADJUSTING CONTROL
As discussed in Chapter 20, some control is necessary in each adjustment. However, since control itself is not perfect, this raises the question of how control should be managed. If control stations that contain errors are overweighted, the adjustment will associate the control errors with the observations improperly. This effect can be removed by using only the minimum amount of control required to fix the project. Table 21.2 lists the type of survey versus the minimum amount of control. Thus, in a horizontal adjustment, if the coordinates of only one station and the direction of only one line are held fixed, the observations will not be constricted by the control. That is, the observations will need to satisfy the internal geometric constraints of the network only. If more than minimum control is used, these additional constraints will be factored into the adjustment.
TABLE 21.2 Requirements for a Minimally Constrained Adjustment
| Survey Type | Minimum Amount of Control |
| Differential leveling | 1 bench mark |
| Horizontal survey | 1 point with known xy coordinates 1 course with known azimuth |
| GNSS survey | 1 point with known geodetic coordinates |
Statistical blunder detection can help identify weak control or the presence of systematic errors in observations. Using a minimally constrained adjustment, the data set is screened for blunders. After becoming confident that the blunders are removed from the data set, an overconstrained adjustment is performed. Following the overconstrained adjustment, an F test is used to compare the ratio of the reference variances from the minimally constrained and overconstrained adjustments. The ratio of the two reference variances should be 1.3
If the two reference variances are found to be statistically different, two possible causes might exist. The first is that there are errors in the control that must be isolated and removed. The second is that the observations contain systematic errors. Since systematic errors are not compensating in nature, they will appear as blunders in the overconstrained adjustment. If systematic errors are suspected, they should be identified and removed from the original data set and the entire adjustment procedure performed again. If no systematic errors are identified,4 different combinations of control stations should be used in the constrained adjustments until the problem is isolated. By following this type of systematic approach, a single control station that has inconsistent coordinates is isolated.
With this stated, it should be realized that the ideal amount of control in each survey type is greater than the minimum. In fact for all three survey types, a minimum of three fixed stations (control) is always preferable. For example, in a differential leveling survey with only two bench marks, it would be impossible to isolate the problem by simply removing one bench mark from the adjustment. However, if three bench marks are used, a separate adjustment containing only two of the bench marks can be run until the offending bench mark is isolated.
Extreme caution should always be used when dealing with control stations. Although it is possible that a control station was disturbed or that the original published coordinates contained errors, this is not always the case. A prudent surveyor should check for physical evidence of disturbance and talk with other surveyors before deciding to discard control. If the station was set by a local, state, or federal agency, the surveyor should contact the proper authorities and report any suspected problems. People in the agency familiar with the control may help explain any apparent problem. For example, it is possible that the control used in the survey was established by two previously nonconnecting surveys. In this case, the relative accuracy of the stations was never checked when they were established. Another common problem with control is the connection of two control points from different realizations of the same reference frame. As an example, suppose a first-order control station from a conventional survey and a High Accuracy Reference Network (HARN) station from a GNSS survey are used as control in a survey, these two stations come from different national adjustments and are thus in different realizations of the same datum. Their coordinates will most likely not agree with each other in an adjustment.
21.8 A DATA SET WITH BLUNDERS
21.9 SOME FURTHER CONSIDERATIONS
![]() Equation (21.14) shows the relationship between blunders and their effects on residuals as Δvi = −ri Δli. From this relationship, note that the effect of the blunder, Δli, on the residual, Δvi, is directly proportional to the redundancy number, ri. Therefore,
Equation (21.14) shows the relationship between blunders and their effects on residuals as Δvi = −ri Δli. From this relationship, note that the effect of the blunder, Δli, on the residual, Δvi, is directly proportional to the redundancy number, ri. Therefore,
- If ri is large (≈ 1), the blunder greatly affects the residual and should be easy to find.
- If ri is small (≈ 0), the blunder has little effect on the residual and will be hard to find.
- If ri = 0 as in the case of spur observations, then the blunder is undetectable, and the solved parameters will be incorrect since the error cannot been detected.
Since redundancy numbers can range from 0 to 1, it is possible to compute the minimum detectable error for a single blunder. For example, suppose that a value of 4.0 is used to isolate observational blunders. Then if the reference variance of the adjustment is 6, all observations that have standardized residuals greater than 24.0 (4.0 × 6) are possible blunders. However, from Equation (21.14), it can be seen that for an observation with a redundancy number of 0.2 (ri = 0.2) and a standardized residual of Δvi = 24.0, the minimum detectable error is 24.0/0.2, or 120! Thus, a blunder, Δli, in this observation as large as five times the desired level can go undetected due to its low redundancy number. This situation can be extended to observations that have no observational checks (spur observations), that is, ri is 0. In this case, Equation (21.14) shows that it is impossible to detect any blunder, Δli, in the observation since Δvi /Δri is indeterminate.
With this taken into consideration, it has been shown (Amer, 1983; Caspary, 1987) that a marginally detectable blunder in an individual observation is
where λ0 is the mean of the noncentral normal distribution shown in Figure 21.5 known as the noncentrality parameter. This parameter is the translation of the normal distribution that leads to rejection of the null hypothesis and whose values can be taken from nomograms developed by Baarda (1968). The sizes of the values obtained from Equation (21.21) provide a clear insight into weak areas of the network.
21.9.1 Internal Reliability
Internal reliability is found by examining how well observations check themselves geometrically. As mentioned previously, if a station is uniquely determined, qii will be zero in Equation (21.21) and the computed value of Δli is infinity. This indicates the lack of self-checking observations. Since Equation (21.21) is independent of the actual observations, it provides a method of detecting weak areas in networks. To minimize the sizes of the undetected blunders in a network, the redundancy numbers of the individual observations should approach their maximum value of 1. Furthermore, for uniform network strength, the individual redundancy numbers, ri, should be close to the global relative redundancy of r/m where r is the number of redundant observations and m is the number of observations in the network. Weak areas in the network are located by finding regions where the redundancy numbers become small in comparison to relative redundancy.
21.9.2 External Reliability
An undetected blunder of size Δli has a direct effect on the adjusted parameters. External reliability is the effect of the undetected blunders on these parameters. As Δli (a blunder) increases, so will its effect on ΔX. The value of ΔX is given by
Again, this equation is datum independent. From Equation (21.22), it can be seen that to minimize the value of ΔXi, the size of redundancy numbers must be increased. Baarda suggested using average coordinate values in determining the effect of an undetected blunder with the following equation
where λ represents the noncentrality parameter.
The noncentrality parameter should remain as small as possible to minimize the effects of undetected blunders on the coordinates. Note that as the redundancy numbers on the observations become small, the effects of undetected blunders become large. Thus, the effect on the coordinates of a station from an undetected blunder is greater when the redundancy number is low. In fact, an observation with a high redundancy number is likely to be detected as a blunder.
A traverse sideshot (spur observation) can be used to explain this phenomenon. Since the angle and distance to the station are unchecked in a sideshot, the coordinates of the station will change according to the size of the observational blunders. The observations creating the sideshot will have redundancy numbers of zero since they are geometrically unchecked. This situation is neither good nor acceptable in a well-designed observational system. In network design, one should always check the redundancy numbers of the anticipated observations and strive to achieve uniformly high values for all observations. Redundancy numbers above 0.5 are generally sufficient to provide well-checked observations.
21.10 SURVEY DESIGN
In Chapters 8 and 19, the topic of observational system design was discussed. Redundancy numbers can now be added to this discussion. A well-designed network will provide sufficient geometric checks to allow observational blunders to be detected and removed. In Section 21.8.1 it was stated that if blunder removal is to occur uniformly throughout the system, the redundancy numbers should be close to the system's global relative redundancy. Furthermore, in Section 21.8.2 it was noted that redundancy numbers should be about 0.5 or greater. By combining these two additional concepts with the error ellipse sizes and shapes, and stochastic model planning, an overall methodology for designing observational systems can be obtained.
To begin the design process, the approximate positions for stations to be included in the survey must be determined. These locations can be determined from topographic maps, photo measurements, code-based GNSS, or previous survey data. The approximate locations of the control stations should be dictated by their desired locations, the surrounding terrain, vegetation, soils, sight line obstructions, and so on. For conventional surveys, field reconnaissance at this phase of the design process is generally worthwhile to verify sight-lines and accessibility of stations. It is also worthwhile in GNSS surveys to ensure adequate sky views are possible from the prospective station locations. At this stage, moving a station only a small distance from the original design location may greatly enhance visibility, but not change the geometry of the network significantly. In conventional surveys, using topographic maps in this process allows one to check sight line ground clearances by constructing profiles between stations. Additionally, websites such as Google Earth provide easy access to recent photography to check overhead visibility clearances in GNSS surveys.
When approximate station coordinates are determined, a stochastic model for the observational system can be designed following the procedures discussed in Chapters 7 and 9. In this design process, considerations should be given to the abilities of the field personnel, quality of the equipment, and observational procedures. After the design is completed, specifications for field crews can be written based on these design parameters. These specifications should include the type of instrument used, number of turnings for angle observations, accuracy of instrument leveling and centering, horizon closure requirements, as well as many other items.
These items should be written in a form that field crews will understand. For example, it is not sufficiently clear to state that the setup error of an instrument must be under ±0.005 ft. It is better to state that level vials and optical plummets for all instruments used in the survey must be calibrated, and the special care must be taken in setting and leveling instruments over a station. If one expects good field work then the instructions to the field crews must be understandable and verifiable.
Once the stochastic model is designed, simulated observations can be computed from the station coordinates, and a least squares adjustment of the simulated observations performed. Since actual observations have not been made, their values are computed from the station coordinates. The adjustment will converge in a single iteration with all residuals equaling zero. Thus, the reference variance must be assigned the a priori value of 1 to compute the error ellipse axes and the standard deviations of the station coordinates. Having completed the adjustment, the network can be checked for geometrically weak areas, unacceptable error ellipse size or shape, and so on. This inspection may dictate the need for any or all of the following: (1) more observations, (2) different observational procedures, (3) different equipment, (4) more stations, (5) different network geometry, and so on. In any event, a clear picture of results obtainable from the observational system will be provided by the simulated adjustment and additional observations, or different network geometry can be used.
In GNSS surveys, it should be realized that the design of the network provides checks on the observational procedures. However, the accuracy of the derived positions is more dependent on the geometry of the satellites, the length of the sessions, and the type of processing than it is on the actual geometry of the survey. Thus, when designing a GNSS survey, strong considerations should be given to station accessibility, satellite visibility, lack of multipath conditions caused by reflective surfaces, positional dilution of precision (PDOP), and length of sessions.
It should be noted that what is expected from the design may not actually occur due to numerous and varied reasons. Thus, systems are generally overdesigned. However, this tendency to overdesign should be tempered with the knowledge that it will raise the costs of the survey. Thus, a balance should be found between the design and costs. Experienced surveyors know what level of accuracy is necessary for each job and design observational systems to achieve the desired accuracy. It would be cost-prohibitive and foolish to always design an observational system for maximum accuracy regardless of the survey's intended use. As an example the final adjustment of the survey in Section 21.7 had sufficient accuracy to be used in a mapping project with a final scale of 1:1200 since the largest error ellipse semimajor axis (0.138 ft) would only plot as 0.0014 in. and is thus less than the width of a line on the final map product.
For convenience, the steps involved in network design are summarized as follows:
- Step 1: Using a topographic map, aerial photos, or website, lay out possible positions for stations.
- Step 2: Use the topographic map together with air photos to check sight lines for possible obstructions and ground clearance.
- Step 3: Do field reconnaissance, checking sight lines for obstructions not shown on the map or photos, and adjust positions of stations as necessary.
- Step 4: Determine approximate coordinates for the stations from the map or photos.
- Step 5: Compute values of observations using the coordinates from step 4.
- Step 6: Using methods discussed in Chapter 6 or 9, compute the standard deviation of each observation based on available equipment, and field measuring procedures.
- Step 7: Perform a least squares adjustment, to compute observational redundancy numbers, standard deviations of station coordinates, and error ellipses at a specified percent probability.
- Step 8: Inspect the solution for weak areas based on redundancy numbers and ellipse shapes. Add or remove observations as necessary, or reevaluate observational procedures and equipment.
- Step 9: Evaluate the costs of the survey, and determine if some other method of measurement (GNSS, for example) may be more cost-effective.
- Step 10: Write specifications for field crews.
21.11 SOFTWARE
Data snooping and the tau criterion have been implemented in ADJUST for differential leveling, horizontal, and GNSS network adjustments. As shown in Figure 21.8, the user can implement either option by selecting it. Once selected, a text box will appear to the right of the option, which defaults to an appropriate rejection criterion. For example, when data snooping is selected, the default rejection level is 3.29. The default level of significance for the tau criterion is 0.001. The user may modify these defaults to suit their situation. As discussed in Section 21.8, the software will compute the standardized residuals and the redundancy numbers for each observation. Additionally, this option should be selected when performing a simulated adjustment so that the redundancy numbers can be scanned for observations that lack sufficient checks.
On the book's companion website is the Mathcad® file C21.xmcd that demonstrates the statistical blunder detection concepts covered in this chapter. Figure 21.9 shows the section of the Mathcad code that is used to compute the standardized residuals and redundancy numbers. For those wishing to program blunder detection using a higher-level language, the Mathcad file C21.xmcd demonstrates the use of blunder detection in analyzing a horizontal network. Furthermore, the computation of the critical tau value has been added to the program STATS. Both of these programs can be found on the book's companion website.

FIGURE 21.9 Mathcad code to compute standardized residuals and redundancy numbers.
PROBLEMS
Note: ADJUST, which is available on the book's companion website should be used to solve the problems requiring a least squares adjustments. Partial answers are provided for problems marked with an asterisk in Appendix H.
- *21.1 Discuss the effects of a distance blunder on a traverse closure and explain how it can be identified.
- 21.2 Discuss the effects of an angle blunder on a traverse closure, and explain how it can be identified.
- 21.3 Explain why it is not wise to have observational redundancy numbers near 0 in a well-designed network.
- 21.4 Create a list of items that should be included in field specifications for a crew in a designed network and then create a sample set of specifications for a horizontal survey.
- 21.5 Summarize the general procedures used in isolating observational blunders.
- 21.6 How are control problems isolated in an adjustment?
- 21.7 Discuss possible causes for control problems in an adjustment.
- 21.8 Why is it recommended that there be at least three control stations in a least squares adjustment?
- 21.9 Outline the procedures used in survey network design.
- *21.10 Using data snooping, analyze the data in Problem 15.10. Hold the control fixed during the adjustment.
- 21.11 Repeat Problem 21.10 using the tau criterion.

- 21.12 Analyze the data in Problem 16.8 using
- (a) Data snooping.
- (b) Tau criterion.
- 21.13 Using data snooping, analyze the data in Problem 15.12 for blunders. Hold the control fixed during the adjustment.
- 21.14 Analyze the data in Problem 15.15 while holding the control station coordinates fixed using
- (a) data snooping.
- (b) tau criterion.

- 21.15 Analyze the data in Problem 16.14 while holding the control station coordinates fixed using
- (a) data snooping.
- (b) tau criterion.
- *21.16 Two control stations that are 12,203.02 ft apart have a published precision of 1:50,000. What are the appropriate estimated errors for the coordinates of these points?
- 21.17 Repeat Problem 21.16 for two stations that are 40,503.645 m apart with a published precision of 1:20,000.
- 21.18 Analyze the data in Problem 16.7 assuming the control points have relative precisions of 1:10,000 using
- (a) data snooping.
- (b) tau criterion.
- 21.19 The standard deviations on the xy coordinates for Station A in Problem 16.14 are ±0.016 ft and ±0.020 ft, respectively. The standard deviations for Station D are ±0.028 ft and ±0.022 ft. Adjust and analyze the data. Be sure to handle the control correctly.
- 21.20 In the accompanying figure, the following data were gathered. Assuming that the control stations have a published precision of 1:10,000, apply the procedures discussed in this chapter to isolate and remove any apparent blunders in the data.
- (a) Use data snooping with a rejection criterion of 3.29.
- (b) Use the tau criterion at a level of significance of 0.001.
- (c) Analyze statistically the constrained and minimally constrained adjustments. Did the two adjustments pass the F test at a level of significance of 0.05?
- (d) At a level of significance of 0.05, does the constrained adjustment pass the χ2 test?
Control Stations Approximate Station Coordinates Station Easting (m) Northing (m) Station Easting (m) Northing (m) A 1105.687 1000.204 B 3205.687 1602.593 D 4609.645 256.789 C 1597.600 200.000 E 1597.600 200.000 F 2814.698 842.358 Distance Observations From To Distance (m) S (m) From To Distance (m) S (m) A B 2184.688 0.008 E F 1376.207 0.006 A F 1716.281 0.007 E A 939.301 0.005 B C 1527.384 0.006 D F 1888.046 0.007 B F 854.876 0.005 D E 3012.591 0.010 C D 741.819 0.005 C F 1800.671 0.007 Angle Observations Backsight Occupied Foresight Angle S (″) F A E 53°08′33.6″ 2.3 B A F 21°16′55.2″ 2.2 F B A 46°46′38.5″ 2.3 C B F 93°55′23.9″ 2.3 F C B 28°16′35.8″ 2.2 D C F 85°06′21.2″ 2.3 F D C 71°50′57.6″ 2.3 E D F 19°08′51.8″ 2.2 A E F 93°45′22.8″ 2.3 F E D 26°44′36.3″ 2.2 A F B 111°56′25.0″ 2.3 B F C 57°48′19.5″ 2.3 C F D 23°02′45.8″ 2.2 D F E 134°06′27.3″ 2.2 E F A 33°06′04.7″ 2.2 - 21.21 Repeat Problem 21.20 with the additional distance observations. Comment on any changes in the redundancy numbers of the observations.
From To Length (m) S (m) C B 1527.379 0.006 F B 854.888 0.005 D C 741.813 0.005 F E 1376.203 0.006 A E 939.320 0.005 - 21.22 Apply to procedures discussed in this chapter to isolate any blunders in the following data. Assume that station A has a relative precision of 1:100,000 and H has a relative precision of 1:50,000.
- (a) Analyze the data using data snooping using a rejection criterion of 3.29.
- (b) Analyze the data using the tau criterion at a level of significance of 0.001.
- (c) Analyze statistically the constrained and minimally constrained adjustments. Did the two adjustments pass the F test at a level of significance of 0.05?
- (d) At a level of significance of 0.05, does the constrained adjustment pass the χ2 test?
Control Stations Approximate Coordinates Station X (ft) Y (ft) Station X (ft) Y (ft) A 45,806.98 80,465.38 B 36,489.48 151,309.33 H 147,608.99 202,654.36 C 49,263.50 202,648.34 D 98,056.35 153,648.04 E 99,121.34 76,098.35 F 144,512.87 74,215.66 G 150,608.77 142,516.35 Distance Observations Course Distance (ft) S (ft) Course Distance (ft) S (ft) AB 71,454.13 0.215 BC 52,904.31 0.159 CD 69,150.62 0.208 DE 77,557.09 0.233 EF 45,430.65 0.137 FG 68,571.96 0.206 GH 60,212.72 0.181 CH 98,345.84 0.295 AE 53,492.61 0.161 AD 89,920.33 0.270 DH 69,692.94 0.210 BD 61,611.51 0.185 DG 53,718.64 0.162 DF 92,022.35 0.276 Angle Observations Backsight Occupied Foresight Angle S (″) B A D 43°01′02.7″ 2.1 D B A 84°40′58.5″ 2.1 C B D 73°51′06.5″ 2.1 D C B 58°51′02.5″ 2.1 H C D 45°07′31.2″ 2.1 D H C 44°40′44.3″ 2.1 G H D 48°10′24.0″ 2.1 D G H 75°11′06.6″ 2.1 F G D 96°51′34.3″ 2.1 D F G 35°25′18.1″ 2.1 E F D 57°18′12.4″ 2.1 A E D 84°31′49.4″ 2.1 D E F 93°09′44.6″ 2.3 D A E 59°09′26.9″ 2.1 A D B 52°18′00.4″ 2.1 B D C 47°17′50.0″ 2.1 C D H 90°11′45.9″ 2.1 H D G 56°38′30.7″ 2.1 G D F 47°43′04.5″ 2.1 F D E 29°32′07.2″ 2.1 E D A 36°18′39.8″ 2.1 - 21.23 Using the data set Blunder.dat, which is part of the installation of the software ADJUST that accompanies this book, isolate any blunders that are detectable using data snooping and a rejection criteria of 3.29.
- 21.24 Repeat Problem 21.23 using the tau criterion and a level of significance of 0.001.
- 21.25 As shown in the accompanying figure, the following approximate station coordinates were determined from a map of an area where a second-order, class I survey (1:50,000) is to be performed. All sight lines to neighboring stations have been checked and are available for conventional observations of distances, angles, and azimuths. The control stations are visible to their nearest neighbors. Design a control network that will meet the specified accuracy at a 95% confidence level and have sufficient checks to ensure the reliability of the results. Stations J218, J219, and ROCK are first-order control stations (1:100,000).
Control Stations Approximate Station Locations Station X (m) Y (m) Station X (m) Y (m) J218 283,224.223 116,202.946 101 280,278 194,109 J219 154,995.165 330,773.314 102 276,350 278,887 ROCK 521,287.251 330,276.310 103 360,147 121,768 104 356,219 195,090 105 352,291 274,304 106 455,728 132,570 107 446,563 198,036 108 440,671 270,700
PRACTICAL PROBLEMS
- 21.1 Design a 6 mile by 6 mile control network having a minimum of eight control stations using a topographic map of your local area. Design a traditional measurement network made up of angles, azimuths, and distances so that the largest ellipse axis at a 95% confidence level is less than 0.20 ft and so that all observations have redundancy numbers greater than 0.5. In the design, specify the shortest permissible sight distance, the largest permissible errors in pointing, reading, and instrument and target setup errors, the number of repetitions necessary for each angle measurement, and the necessary quality of angle and distance measuring instruments. Use realistic values for the instruments. Plot profiles of sight lines for each observation.
- 21.2 Design a 6 mile by 6 mile GNSS control network to be established by differential GNSS that has a minimum of eight control stations using a topographic map of your local area to select station locations. Design the survey so that all baseline observations included in the network have redundancy numbers greater than 0.5. In the design, use a unit matrix for the covariance matrix of the baselines.