Chapter
7
List and Iterator ADTs

Contents
7.2.2 Implementing a Dynamic Array
7.2.3 Amortized Analysis of Dynamic Arrays
7.2.4 Java's StringBuilder class
7.3.2 The Positional List Abstract Data Type
7.3.3 Doubly Linked List Implementation
7.4.1 The Iterable Interface and Java's For-Each Loop
7.5 The Java Collections Framework
7.5.2 Comparison to Our Positional List ADT
7.5.3 List-Based Algorithms in the Java Collections Framework
7.7 Case Study: Maintaining Access Frequencies
7.1 The List ADT
In Chapter 6, we introduced the stack, queue, and deque abstract data types, and discussed how either an array or a linked list could be used for storage in an efficient concrete implementation of each. Each of those ADTs represents a linearly ordered sequence of elements. The deque is the most general of the three, yet even so, it only allows insertions and deletions at the front or back of a sequence.
In this chapter, we explore several abstract data types that represent a linear sequence of elements, but with more general support for adding or removing elements at arbitrary positions. However, designing a single abstraction that is well suited for efficient implementation with either an array or a linked list is challenging, given the very different nature of these two fundamental data structures.
Locations within an array are easily described with an integer index. Recall that an index of an element e in a sequence is equal to the number of elements before e in that sequence. By this definition, the first element of a sequence has index 0, and the last has index n − 1, assuming that n denotes the total number of elements. The notion of an element's index is well defined for a linked list as well, although we will see that it is not as convenient of a notion, as there is no way to efficiently access an element at a given index without traversing a portion of the linked list that depends upon the magnitude of the index.
With that said, Java defines a general interface, java.util.List, that includes the following index-based methods (and more):
| size(): | Returns the number of elements in the list. |
| isEmpty(): | Returns a boolean indicating whether the list is empty. |
| get(i): | Returns the element of the list having index i; an error condition occurs if i is not in range [0, size() − 1]. |
| set(i, e): | Replaces the element at index i with e, and returns the old element that was replaced; an error condition occurs if i is not in range [0, size() − 1]. |
| add(i, e): | Inserts a new element e into the list so that it has index i, moving all subsequent elements one index later in the list; an error condition occurs if i is not in range [0, size()]. |
| remove(i): | Removes and returns the element at index i, moving all subsequent elements one index earlier in the list; an error condition occurs if i is not in range [0, size() − 1]. |
We note that the index of an existing element may change over time, as other elements are added or removed in front of it. We also draw attention to the fact that the range of valid indices for the add method includes the current size of the list, in which case the new element becomes the last.
Example 7.1 demonstrates a series of operations on a list instance, and Code Fragment 7.1 below provides a formal definition of our simplified version of the List interface; we use an IndexOutOfBoundsException to signal an invalid index argument.
Example 7.1: We demonstrate operations on an initially empty list of characters.
Code Fragment 7.1: A simple version of the List interface.
7.2 Array Lists
An obvious choice for implementing the list ADT is to use an array A, where A[i] stores (a reference to) the element with index i. We will begin by assuming that we have a fixed-capacity array, but in Section 7.2.1 describe a more advanced technique that effectively allows an array-based list to have unbounded capacity. Such an unbounded list is known as an array list in Java (or a vector in C++ and in the earliest versions of Java).
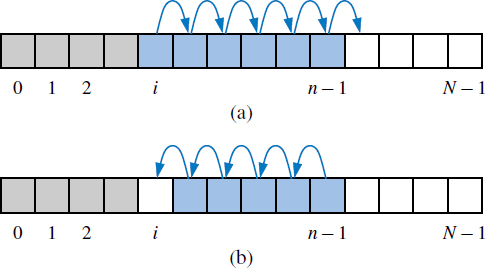
With a representation based on an array A, the get(i) and set(i, e) methods are easy to implement by accessing A[i] (assuming i is a legitimate index). Methods add(i, e) and remove(i) are more time consuming, as they require shifting elements up or down to maintain our rule of always storing an element whose list index is i at index i of the array. (See Figure 7.1.) Our initial implementation of the ArrayList class follows in Code Fragments 7.2 and 7.3.
Figure 7.1: Array-based implementation of an array list that is storing n elements: (a) shifting up for an insertion at index i; (b) shifting down for a removal at index i.
Code Fragment 7.2: An implementation of a simple ArrayList class with bounded capacity. (Continues in Code Fragment 7.3.)
Code Fragment 7.3: An implementation of a simple ArrayList class with bounded capacity. (Continued from Code Fragment 7.2.)
The Performance of a Simple Array-Based Implementation
Table 7.1 shows the worst-case running times of the methods of an array list with n elements realized by means of an array. Methods isEmpty, size, get and set clearly run in O(1) time, but the insertion and removal methods can take much longer than this. In particular, add(i, e) runs in time O(n). Indeed, the worst case for this operation occurs when i is 0, since all the existing n elements have to be shifted forward. A similar argument applies to method remove(i), which runs in O(n) time, because we have to shift backward n − 1 elements in the worst case, when i is 0. In fact, assuming that each possible index is equally likely to be passed as an argument to these operations, their average running time is O(n), for we will have to shift n/2 elements on average.
| Method | Running Time |
| size() | O(1) |
| isEmpty() | O(1) |
| get(i) | O(1) |
| set(i, e) | O(1) |
| add(i, e) | O(n) |
| remove(i) | O(n) |
Table 7.1: Performance of an array list with n elements realized by a fixed-capacity array.
Looking more closely at add(i, e) and remove(i), we note that they each run in time O(n − i + 1), for only those elements at index i and higher have to be shifted up or down. Thus, inserting or removing an item at the end of an array list, using the methods add(n, e) and remove(n − 1) respectively, takes O(1) time each. Moreover, this observation has an interesting consequence for the adaptation of the array list ADT to the deque ADT from Section 6.3.1. If we do the “obvious” thing and store elements of a deque so that the first element is at index 0 and the last element at index n − 1, then methods addLast and removeLast of the deque each run in O(1) time. However, methods addFirst and removeFirst of the deque each run in O(n) time.
Actually, with a little effort, we can produce an array-based implementation of the array list ADT that achieves O(1) time for insertions and removals at index 0, as well as insertions and removals at the end of the array list. Achieving this requires that we give up on our rule that an element at index i is stored in the array at index i, however, as we would have to use a circular array approach like the one we used in Section 6.2 to implement a queue. We leave the details of this implementation as Exercise C-7.25.
7.2.1 Dynamic Arrays
The ArrayList implementation in Code Fragments 7.2 and 7.3 (as well as those for a stack, queue, and deque from Chapter 6) has a serious limitation; it requires that a fixed maximum capacity be declared, throwing an exception if attempting to add an element once full. This is a major weakness, because if a user is unsure of the maximum size that will be reached for a collection, there is risk that either too large of an array will be requested, causing an inefficient waste of memory, or that too small of an array will be requested, causing a fatal error when exhausting that capacity.
Java's ArrayList class provides a more robust abstraction, allowing a user to add elements to the list, with no apparent limit on the overall capacity. To provide this abstraction, Java relies on an algorithmic sleight of hand that is known as a dynamic array.
In reality, elements of an ArrayList are stored in a traditional array, and the precise size of that traditional array must be internally declared in order for the system to properly allocate a consecutive piece of memory for its storage. For example, Figure 7.2 displays an array with 12 cells that might be stored in memory locations 2146 through 2157 on a computer system.
Figure 7.2: An array of 12 cells, allocated in memory locations 2146 through 2157.
Because the system may allocate neighboring memory locations to store other data, the capacity of an array cannot be increased by expanding into subsequent cells.
The first key to providing the semantics of an unbounded array is that an array list instance maintains an internal array that often has greater capacity than the current length of the list. For example, while a user may have created a list with five elements, the system may have reserved an underlying array capable of storing eight object references (rather than only five). This extra capacity makes it easy to add a new element to the end of the list by using the next available cell of the array.
If a user continues to add elements to a list, all reserved capacity in the underlying array will eventually be exhausted. In that case, the class requests a new, larger array from the system, and copies all references from the smaller array into the beginning of the new array. At that point in time, the old array is no longer needed, so it can be reclaimed by the system. Intuitively, this strategy is much like that of the hermit crab, which moves into a larger shell when it outgrows its previous one.
7.2.2 Implementing a Dynamic Array
We now demonstrate how our original version of the ArrayList, from Code Fragments 7.2 and 7.3, can be transformed to a dynamic-array implementation, having unbounded capacity. We rely on the same internal representation, with a traditional array A, that is initialized either to a default capacity or to one specified as a parameter to the constructor.
The key is to provide means to “grow” the array A, when more space is needed. Of course, we cannot actually grow that array, as its capacity is fixed. Instead, when a call to add a new element risks overflowing the current array, we perform the following additional steps:
- Allocate a new array B with larger capacity.
- Set B[k] = A[k], for k = 0,..., n − 1, where n denotes current number of items.
- Set A = B, that is, we henceforth use the new array to support the list.
- Insert the new element in the new array.
An illustration of this process is shown in Figure 7.3.
Figure 7.3: An illustration of “growing” a dynamic array: (a) create new array B; (b) store elements of A in B; (c) reassign reference A to the new array. Not shown is the future garbage collection of the old array, or the insertion of a new element.
Code Fragment 7.4 provides a concrete implementation of a resize method, which should be included as a protected method within the original ArrayList class. The instance variable data corresponds to array A in the above discussion, and local variable temp corresponds to array B.
Code Fragment 7.4: An implementation of the ArrayList.resize method.
The remaining issue to consider is how large of a new array to create. A commonly used rule is for the new array to have twice the capacity of the existing array that has been filled. In Section 7.2.3, we will provide a mathematical analysis to justify such a choice.
To complete the revision to our original ArrayList implementation, we redesign the add method so that it calls the new resize utility when detecting that the current array is filled (rather than throwing an exception). The revised version appears in Code Fragment 7.5.
Code Fragment 7.5: A revision to the ArrayList.add method, originally from Code Fragment 7.3, which calls the resize method of Code Fragment 7.4 when more capacity is needed.
Finally, we note that our original implementation of the ArrayList class includes two constructors: a default constructor that uses an initial capacity of 16, and a parameterized constructor that allows the caller to specify a capacity value. With the use of dynamic arrays, that capacity is no longer a fixed limit. Still, greater efficiency is achieved when a user selects an initial capacity that matches the actual size of a data set, as this can avoid time spent on intermediate array reallocations and potential space that is wasted by having too large of an array.
7.2.3 Amortized Analysis of Dynamic Arrays
In this section, we will perform a detailed analysis of the running time of operations on dynamic arrays. As a shorthand notation, let us refer to the insertion of an element to be the last element in an array list as a push operation.
The strategy of replacing an array with a new, larger array might at first seem slow, because a single push operation may require Ω(n) time to perform, where n is the current number of elements in the array. (Recall, from Section 4.3.1, that big-Omega notation, describes an asymptotic lower bound on the running time of an algorithm.) However, by doubling the capacity during an array replacement, our new array allows us to add n further elements before the array must be replaced again. In this way, there are many simple push operations for each expensive one (see Figure 7.4). This fact allows us to show that a series of push operations on an initially empty dynamic array is efficient in terms of its total running time.
Figure 7.4: Running times of a series of push operations on a dynamic array.
Using an algorithmic design pattern called amortization, we show that performing a sequence of push operations on a dynamic array is actually quite efficient. To perform an amortized analysis, we use an accounting technique where we view the computer as a coin-operated appliance that requires the payment of one cyber-dollar for a constant amount of computing time. When an operation is executed, we should have enough cyber-dollars available in our current “bank account” to pay for that operation's running time. Thus, the total amount of cyber-dollars spent for any computation will be proportional to the total time spent on that computation. The beauty of using this analysis method is that we can overcharge some operations in order to save up cyber-dollars to pay for others.
Proposition 7.2: Let L be an initially empty array list with capacity one, implemented by means of a dynamic array that doubles in size when full. The total time to perform a series of n push operations in L is O(n).
Justification: Let us assume that one cyber-dollar is enough to pay for the execution of each push operation in L, excluding the time spent for growing the array. Also, let us assume that growing the array from size k to size 2k requires k cyber-dollars for the time spent initializing the new array. We shall charge each push operation three cyber-dollars. Thus, we overcharge each push operation that does not cause an overflow by two cyber-dollars. Think of the two cyber-dollars profited in an insertion that does not grow the array as being “stored” with the cell in which the element was inserted. An overflow occurs when the array L has 2i elements, for some integer i ≥ 0, and the size of the array used by the array representing L is 2i. Thus, doubling the size of the array will require 2i cyber-dollars. Fortunately, these cyber-dollars can be found stored in cells 2i−1 through 2i − 1. (See Figure 7.5.)
Figure 7.5: Illustration of a series of push operations on a dynamic array: (a) an 8-cell array is full, with two cyber-dollars “stored” at cells 4 through 7; (b) a push operation causes an overflow and a doubling of capacity. Copying the eight old elements to the new array is paid for by the cyber-dollars already stored in the table. Inserting the new element is paid for by one of the cyber-dollars charged to the current push operation, and the two cyber-dollars profited are stored at cell 8.
Note that the previous overflow occurred when the number of elements became larger than 2i−1 for the first time, and thus the cyber-dollars stored in cells 2i−1 through 2i − 1 have not yet been spent. Therefore, we have a valid amortization scheme in which each operation is charged three cyber-dollars and all the computing time is paid for. That is, we can pay for the execution of n push operations using 3n cyber-dollars. In other words, the amortized running time of each push operation is O(1); hence, the total running time of n push operations is O(n).
Geometric Increase in Capacity
Although the proof of Proposition 7.2 relies on the array being doubled each time it is expanded, the O(1) amortized bound per operation can be proven for any geometrically increasing progression of array sizes. (See Section 2.2.3 for discussion of geometric progressions.) When choosing the geometric base, there exists a tradeoff between runtime efficiency and memory usage. If the last insertion causes a resize event, with a base of 2 (i.e., doubling the array), the array essentially ends up twice as large as it needs to be. If we instead increase the array by only 25% of its current size (i.e., a geometric base of 1.25), we do not risk wasting as much memory in the end, but there will be more intermediate resize events along the way. Still it is possible to prove an O(1) amortized bound, using a constant factor greater than the 3 cyber-dollars per operation used in the proof of Proposition 7.2 (see Exercise R-7.7). The key to the performance is that the amount of additional space is proportional to the current size of the array.
Beware of Arithmetic Progression
To avoid reserving too much space at once, it might be tempting to implement a dynamic array with a strategy in which a constant number of additional cells are reserved each time an array is resized. Unfortunately, the overall performance of such a strategy is significantly worse. At an extreme, an increase of only one cell causes each push operation to resize the array, leading to a familiar 1 + 2 + 3 + ... + n summation and Ω(n2) overall cost. Using increases of 2 or 3 at a time is slightly better, as portrayed in Figure 7.4, but the overall cost remains quadratic.
Figure 7.6: Running times of a series of push operations on a dynamic array using arithmetic progression of sizes. Part (a) assumes an increase of 2 in the size of the array, while part (b) assumes an increase of 3.
Using a fixed increment for each resize, and thus an arithmetic progression of intermediate array sizes, results in an overall time that is quadratic in the number of operations, as shown in the following proposition. In essence, even an increase in 10,000 cells per resize will become insignificant for large data sets.
Proposition 7.3: Performing a series of n push operations on an initially empty dynamic array using a fixed increment with each resize takes Ω(n2) time.
Justification: Let c > 0 represent the fixed increment in capacity that is used for each resize event. During the series of n push operations, time will have been spent initializing arrays of size c, 2c, 3c, ..., mc for ![]() , and therefore, the overall time is proportional to c + 2c + 3c + ... + mc. By Proposition 4.3, this sum is
, and therefore, the overall time is proportional to c + 2c + 3c + ... + mc. By Proposition 4.3, this sum is

Therefore, performing the n push operations takes Ω(n2) time.
Memory Usage and Shrinking an Array
Another consequence of the rule of a geometric increase in capacity when adding to a dynamic array is that the final array size is guaranteed to be proportional to the overall number of elements. That is, the data structure uses O(n) memory. This is a very desirable property for a data structure.
If a container, such as an array list, provides operations that cause the removal of one or more elements, greater care must be taken to ensure that a dynamic array guarantees O(n) memory usage. The risk is that repeated insertions may cause the underlying array to grow arbitrarily large, and that there will no longer be a proportional relationship between the actual number of elements and the array capacity after many elements are removed.
A robust implementation of such a data structure will shrink the underlying array, on occasion, while maintaining the O(1) amortized bound on individual operations. However, care must be taken to ensure that the structure cannot rapidly oscillate between growing and shrinking the underlying array, in which case the amortized bound would not be achieved. In Exercise C-7.29, we explore a strategy in which the array capacity is halved whenever the number of actual element falls below one-fourth of that capacity, thereby guaranteeing that the array capacity is at most four times the number of elements; we explore the amortized analysis of such a strategy in Exercises C-7.30 and C-7.31.
7.2.4 Java's StringBuilder class
Near the beginning of Chapter 4, we described an experiment in which we compared two algorithms for composing a long string (Code Fragment 4.2). The first of those relied on repeated concatenation using the String class, and the second relied on use of Java's StringBuilder class. We observed the StringBuilder was significantly faster, with empirical evidence that suggested a quadratic running time for the algorithm with repeated concatenations, and a linear running time for the algorithm with the StringBuilder. We are now able to explain the theoretical under-pinning for those observations.
The StringBuilder class represents a mutable string by storing characters in a dynamic array. With analysis similar to Proposition 7.2, it guarantees that a series of append operations resulting in a string of length n execute in a combined time of O(n). (Insertions at positions other than the end of a string builder do not carry this guarantee, just as they do not for an ArrayList.)
In contrast, the repeated use of string concatenation requires quadratic time. We originally analyzed that algorithm on page 172 of Chapter 4. In effect, that approach is akin to a dynamic array with an arithmetic progression of size one, repeatedly copying all characters from one array to a new array with size one greater than before.
7.3 Positional Lists
When working with array-based sequences, integer indices provide an excellent means for describing the location of an element, or the location at which an insertion or deletion should take place. However, numeric indices are not a good choice for describing positions within a linked list because, knowing only an element's index, the only way to reach it is to traverse the list incrementally from its beginning or end, counting elements along the way.
Furthermore, indices are not a good abstraction for describing a more local view of a position in a sequence, because the index of an entry changes over time due to insertions or deletions that happen earlier in the sequence. For example, it may not be convenient to describe the location of a person waiting in line based on the index, as that requires knowledge of precisely how far away that person is from the front of the line. We prefer an abstraction, as characterized in Figure 7.7, in which there is some other means for describing a position.
Figure 7.7: We wish to be able to identify the position of an element in a sequence without the use of an integer index. The label “me” represents some abstraction that identifies the position.
Our goal is to design an abstract data type that provides a user a way to refer to elements anywhere in a sequence, and to perform arbitrary insertions and deletions. This would allow us to efficiently describe actions such as a person deciding to leave the line before reaching the front, or allowing a friend to “cut” into line right behind him or her.
As another example, a text document can be viewed as a long sequence of characters. A word processor uses the abstraction of a cursor to describe a position within the document without explicit use of an integer index, allowing operations such as “delete the character at the cursor” or “insert a new character just after the cursor.” Furthermore, we may be able to refer to an inherent position within a document, such as the beginning of a particular chapter, without relying on a character index (or even a chapter number) that may change as the document evolves.
For these reasons, we temporarily forego the index-based methods of Java's formal List interface, and instead develop our own abstract data type that we denote as a positional list. Although a positional list is an abstraction, and need not rely on a linked list for its implementation, we certainly have a linked list in mind as we design the ADT, ensuring that it takes best advantage of particular capabilities of a linked list, such as O(1)-time insertions and deletions at arbitrary positions (something that is not possible with an array-based sequence).
We face an immediate challenge in designing the ADT; to achieve constant time insertions and deletions at arbitrary locations, we effectively need a reference to the node at which an element is stored. It is therefore very tempting to develop an ADT in which a node reference serves as the mechanism for describing a position. In fact, our DoublyLinkedList class of Section 3.4.1 has methods addBetween and remove that accept node references as parameters; however, we intentionally declared those methods as private.
Unfortunately, the public use of nodes in the ADT would violate the object-oriented design principles of abstraction and encapsulation, which were introduced in Chapter 2. There are several reasons to prefer that we encapsulate the nodes of a linked list, for both our sake and for the benefit of users of our abstraction:
- It will be simpler for users of our data structure if they are not bothered with unnecessary details of our implementation, such as low-level manipulation of nodes, or our reliance on the use of sentinel nodes. Notice that to use the addBetween method of our DoublyLinkedList class to add a node at the beginning of a sequence, the header sentinel must be sent as a parameter.
- We can provide a more robust data structure if we do not permit users to directly access or manipulate the nodes. We can then ensure that users do not invalidate the consistency of a list by mismanaging the linking of nodes. A more subtle problem arises if a user were allowed to call the addBetween or remove method of our DoublyLinkedList class, sending a node that does not belong to the given list as a parameter. (Go back and look at that code and see why it causes a problem!)
- By better encapsulating the internal details of our implementation, we have greater flexibility to redesign the data structure and improve its performance. In fact, with a well-designed abstraction, we can provide a notion of a nonnumeric position, even if using an array-based sequence. (See Exercise C-7.43.)
Therefore, in defining the positional list ADT, we also introduce the concept of a position, which formalizes the intuitive notion of the “location” of an element relative to others in the list. (When we do use a linked list for the implementation, we will later see how we can privately use node references as natural manifestations of positions.)
7.3.1 Positions
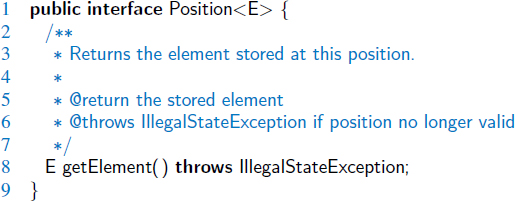
To provide a general abstraction for the location of an element within a structure, we define a simple position abstract data type. A position supports the following single method:
| getElement(): | Returns the element stored at this position. |
A position acts as a marker or token within a broader positional list. A position p, which is associated with some element e in a list L, does not change, even if the index of e changes in L due to insertions or deletions elsewhere in the list. Nor does position p change if we replace the element e stored at p with another element. The only way in which a position becomes invalid is if that position (and its element) are explicitly removed from the list.
Having a formal definition of a position type allows positions to serve as parameters to some methods and return values from other methods of the positional list ADT, which we next describe.
7.3.2 The Positional List Abstract Data Type
We now view a positional list as a collection of positions, each of which stores an element. The accessor methods provided by the positional list ADT include the following, for a list L:
| first(): | Returns the position of the first element of L (or null if empty). |
| last(): | Returns the position of the last element of L (or null if empty). |
| before(p): | Returns the position of L immediately before position p (or null if p is the first position). |
| after(p): | Returns the position of L immediately after position p (or null if p is the last position). |
| isEmpty(): | Returns true if list L does not contain any elements. |
| size(): | Returns the number of elements in list L. |
An error occurs if a position p, sent as a parameter to a method, is not a valid position for the list.
Note well that the first() and last() methods of the positional list ADT return the associated positions, not the elements. (This is in contrast to the corresponding first and last methods of the deque ADT.) The first element of a positional list can be determined by subsequently invoking the getElement method on that position, as first().getElement. The advantage of receiving a position as a return value is that we can subsequently use that position to traverse the list.
As a demonstration of a typical traversal of a positional list, Code Fragment 7.6 traverses a list, named guests, that stores string elements, and prints each element while traversing from the beginning of the list to the end.
Code Fragment 7.6: A traversal of a positional list.
This code relies on the convention that the null reference is returned when the after method is called upon the last position. (That return value is clearly distinguishable from any legitimate position.) The positional list ADT similarly indicates that the null value is returned when the before method is invoked at the front of the list, or when first or last methods are called upon an empty list. Therefore, the above code fragment works correctly even if the guests list is empty.
Updated Methods of a Positional List
The positional list ADT also includes the following update methods:
| addFirst(e): | Inserts a new element e at the front of the list, returning the position of the new element. |
| addLast(e): | Inserts a new element e at the back of the list, returning the position of the new element. |
| addBefore(p, e): | Inserts a new element e in the list, just before position p, returning the position of the new element. |
| addAfter(p, e): | Inserts a new element e in the list, just after position p, returning the position of the new element. |
| set(p, e): | Replaces the element at position p with element e, returning the element formerly at position p. |
| remove(p): | Removes and returns the element at position p in the list, invalidating the position. |
There may at first seem to be redundancy in the above repertoire of operations for the positional list ADT, since we can perform operation addFirst(e) with addBefore(first(), e), and operation addLast(e) with addAfter(last(), e). But these substitutions can only be done for a nonempty list.
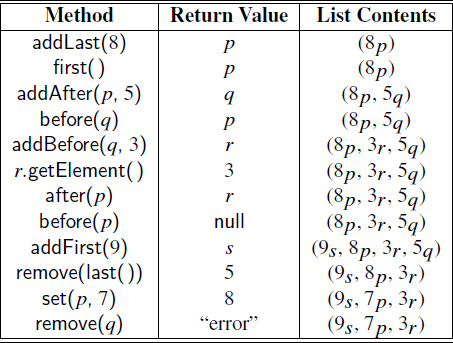
Example 7.4: The following table shows a series of operations on an initially empty positional list storing integers. To identify position instances, we use variables such as p and q. For ease of exposition, when displaying the list contents, we use subscript notation to denote the position storing an element.
Java Interface Definitions
We are now ready to formalize the position ADT and positional list ADT. A Java Position interface, representing the position ADT, is given in Code Fragment 7.7. Following that, Code Fragment 7.8 presents a Java definition for our PositionalList interface. If the getElement() method is called on a Position instance that has previously been removed from its list, an IllegalStateException is thrown. If an invalid Position instance is sent as a parameter to a method of a PositionalList, an IllegalArgumentException is thrown. (Both of those exception types are defined in the standard Java hierarchy.)
Code Fragment 7.7: The Position interface.
Code Fragment 7.8: The PositionalList interface.
7.3.3 Doubly Linked List Implementation
Not surprisingly, our preferred implementation of the PositionalList interface relies on a doubly linked list. Although we implemented a DoublyLinkedList class in Chapter 3, that class does not adhere to the PositionalList interface.
In this section, we develop a concrete implementation of the PositionalList interface using a doubly linked list. The low-level details of our new linked-list representation, such as the use of header and trailer sentinels, will be identical to our earlier version; we refer the reader to Section 3.4 for a discussion of the doubly linked list operations. What differs in this section is our management of the positional abstraction.
The obvious way to identify locations within a linked list are node references. Therefore, we declare the nested Node class of our linked list so as to implement the Position interface, supporting the required getElement method. So the nodes are the positions. Yet, the Node class is declared as private, to maintain proper encapsulation. All of the public methods of the positional list rely on the Position type, so although we know we are sending and receiving nodes, these are only known to be positions from the outside; as a result, users of our class cannot call any method other than getElement().
In Code Fragments 7.9–7.12, we define a LinkedPositionalList class, which implements the positional list ADT. We provide the following guide to that code:
- Code Fragment 7.9 contains the definition of the nested Node<E> class, which implements the Position<E> interface. Following that are the declaration of the instance variables of the outer LinkedPositionalList class and its constructor.
- Code Fragment 7.10 begins with two important utility methods that help us robustly cast between the Position and Node types. The validate(p) method is called anytime the user sends a Position instance as a parameter. It throws an exception if it determines that the position is invalid, and otherwise returns that instance, implicitly cast as a Node, so that methods of the Node class can subsequently be called. The private position(node) method is used when about to return a Position to the user. Its primary purpose is to make sure that we do not expose either sentinel node to a caller, returning a null reference in such a case. We rely on both of these private utility methods in the public accessor methods that follow.
- Code Fragment 7.11 provides most of the public update methods, relying on a private addBetween method to unify the implementations of the various insertion operations.
- Code Fragment 7.12 provides the public remove method. Note that it sets all fields of the removed node back to null—a condition we can later detect to recognize a defunct position.
Code Fragment 7.9: An implementation of the LinkedPositionalList class. (Continues in Code Fragments 7.10–7.12.)
Code Fragment 7.10: An implementation of the LinkedPositionalList class. (Continued from Code Fragment 7.9; continues in Code Fragments 7.11 and 7.12.)
Code Fragment 7.11: An implementation of the LinkedPositionalList class. (Continued from Code Fragments 7.9 and 7.10; continues in Code Fragment 7.12.)
Code Fragment 7.12: An implementation of the LinkedPositionalList class. (Continued from Code Fragments 7.9–7.11.)
The Performance of a Linked Positional List
The positional list ADT is ideally suited for implementation with a doubly linked list, as all operations run in worst-case constant time, as shown in Table 7.2. This is in stark contrast to the ArrayList structure (analyzed in Table 7.1), which requires linear time for insertions or deletions at arbitrary positions, due to the need for a loop to shift other elements.
Of course, our positional list does not support the index-based methods of the official List interface of Section 7.1. It is possible to add support for those methods by traversing the list while counting nodes (see Exercise C-7.38), but that requires time proportional to the sublist that is traversed.
| Method | Running Time |
| size() | O(1) |
| isEmpty() | O(1) |
| first(), last() | O(1) |
| before(p), after(p) | O(1) |
| addFirst(e), addLast(e) | O(1) |
| addBefore(p, e), addAfter(p, e) | O(1) |
| set(p, e) | O(1) |
| remove(p) | O(1) |
Table 7.2: Performance of a positional list with n elements realized by a doubly linked list. The space usage is O(n).
Implementing a Positional List with an Array
We can implement a positional list L using an array A for storage, but some care is necessary in designing objects that will serve as positions. At first glance, it would seem that a position p need only store the index i at which its associated element is stored within the array. We can then implement method getElement(p) simply by returning A[i]. The problem with this approach is that the index of an element e changes when other insertions or deletions occur before it. If we have already returned a position p associated with element e that stores an outdated index i to a user, the wrong array cell would be accessed when the position was used. (Remember that positions in a positional list should always be defined relative to their neighboring positions, not their indices.)
Hence, if we are going to implement a positional list with an array, we need a different approach. We recommend the following representation. Instead of storing the elements of L directly in array A, we store a new kind of position object in each cell of A. A position p stores the element e as well as the current index i of that element within the list. Such a data structure is illustrated in Figure 7.8.
Figure 7.8: An array-based representation of a positional list.
With this representation, we can determine the index currently associated with a position, and we can determine the position currently associated with a specific index. We can therefore implement an accessor, such as before(p), by finding the index of the given position and using the array to find the neighboring position.
When an element is inserted or deleted somewhere in the list, we can loop through the array to update the index variable stored in all later positions in the list that are shifted during the update.
Efficiency Trade-Offs with an Array-Based Sequence
In this array implementation of a sequence, the addFirst, addBefore, addAfter, and remove methods take O(n) time, because we have to shift position objects to make room for the new position or to fill in the hole created by the removal of the old position (just as in the insert and remove methods based on index). All the other position-based methods take O(1) time.
7.4 Iterators
An iterator is a software design pattern that abstracts the process of scanning through a sequence of elements, one element at a time. The underlying elements might be stored in a container class, streaming through a network, or generated by a series of computations.
In order to unify the treatment and syntax for iterating objects in a way that is independent from a specific organization, Java defines the java.util.Iterator interface with the following two methods:
| hasNext(): | Returns true if there is at least one additional element in the sequence, and false otherwise. |
| next(): | Returns the next element in the sequence. |
The interface uses Java's generic framework, with the next() method returning a parameterized element type. For example, the Scanner class (described in Section 1.6) formally implements the Iterator<String> interface, with its next() method returning a String instance.
If the next() method of an iterator is called when no further elements are available, a NoSuchElementException is thrown. Of course, the hasNext() method can be used to detect that condition before calling next().
The combination of these two methods allows a general loop construct for processing elements of the iterator. For example, if we let variable, iter, denote an instance of the Iterator<String> type, then we can write the following:
while (iter.hasNext()) {
String value = iter.next();
System.out .println(value);
}
The java.util.Iterator interface contains a third method, which is optionally supported by some iterators:
| remove(): | Removes from the collection the element returned by the most recent call to next(). Throws an IllegalStateException if next has not yet been called, or if remove was already called since the most recent call to next. |
This method can be used to filter a collection of elements, for example to discard all negative numbers from a data set.
For the sake of simplicity, we will not implement the remove method for most data structures in this book, but we will give two tangible examples later in this section. If removal is not supported, an UnsupportedOperationException is conventionally thrown.
7.4.1 The Iterable Interface and Java's For-Each Loop
A single iterator instance supports only one pass through a collection; calls to next can be made until all elements have been reported, but there is no way to “reset” the iterator back to the beginning of the sequence.
However, a data structure that wishes to allow repeated iterations can support a method that returns a new iterator, each time it is called. To provide greater standardization, Java defines another parameterized interface, named Iterable, that includes the following single method:
| iterator(): | Returns an iterator of the elements in the collection. |
An instance of a typical collection class in Java, such as an ArrayList, is iterable (but not itself an iterator); it produces an iterator for its collection as the return value of the iterator() method. Each call to iterator() returns a new iterator instance, thereby allowing multiple (even simultaneous) traversals of a collection.
Java's Iterable class also plays a fundamental role in support of the “for-each” loop syntax (described in Section 1.5.2). The loop syntax,
for (ElementType variable : collection) { loopBody // may refer to "variable" }
is supported for any instance, collection, of an iterable class. ElementType must be the type of object returned by its iterator, and variable will take on element values within the loopBody. Essentially, this syntax is shorthand for the following:
Iterator<ElementType> iter = collection.iterator(); while (iter.hasNext()) { ElementType variable = iter.next(); loopBody // may refer to "variable" }
We note that the iterator's remove method cannot be invoked when using the for-each loop syntax. Instead, we must explicitly use an iterator. As an example, the following loop can be used to remove all negative numbers from an ArrayList of floating-point values.
ArrayList<Double> data; // populate with random numbers (not shown) Iterator<Double> walk = data.iterator(); while (walk.hasNext()) if (walk.next() < 0.0) walk.remove();
7.4.2 Implementing Iterators
There are two general styles for implementing iterators that differ in terms of what work is done when the iterator instance is first created, and what work is done each time the iterator is advanced with a call to next().
A snapshot iterator maintains its own private copy of the sequence of elements, which is constructed at the time the iterator object is created. It effectively records a “snapshot” of the sequence of elements at the time the iterator is created, and is therefore unaffected by any subsequent changes to the primary collection that may occur. Implementing snapshot iterators tends to be very easy, as it requires a simple traversal of the primary structure. The downside of this style of iterator is that it requires O(n) time and O(n) auxiliary space, upon construction, to copy and store a collection of n elements.
A lazy iterator is one that does not make an upfront copy, instead performing a piecewise traversal of the primary structure only when the next() method is called to request another element. The advantage of this style of iterator is that it can typically be implemented so the iterator requires only O(1) space and O(1) construction time. One downside (or feature) of a lazy iterator is that its behavior is affected if the primary structure is modified (by means other than by the iterator's own remove method) before the iteration completes. Many of the iterators in Java's libraries implement a “fail-fast” behavior that immediately invalidates such an iterator if its underlying collection is modified unexpectedly.
We will demonstrate how to implement iterators for both the ArrayList and LinkedPositionalList classes as examples. We implement lazy iterators for both, including support for the remove operation (but without any fail-fast guarantee).
Iterations with the ArrayList class
We begin by discussing iteration for the ArrayList<E> class. We will have it implement the Iterable<E> interface. (In fact, that requirement is already part of Java's List interface.) Therefore, we must add an iterator() method to that class definition, which returns an instance of an object that implements the Iterator<E> interface. For this purpose, we define a new class, ArrayIterator, as a nonstatic nested class of ArrayList (i.e., an inner class, as described in Section 2.6). The advantage of having the iterator as an inner class is that it can access private fields (such as the array A) that are members of the containing list.
Our implementation is given in Code Fragment 7.13. The iterator() method of ArrayList returns a new instance of the inner ArrayIterator class. Each iterator maintains a field j that represents the index of the next element to be returned. It is initialized to 0, and when j reaches the size of the list, there are no more elements to return. In order to support element removal through the iterator, we also maintain a boolean variable that denotes whether a call to remove is currently permissible.
Code Fragment 7.13: Code providing support for ArrayList iterators. (This should be nested within the ArrayList class definition of Code Fragments 7.2 and 7.3.)
Iterations with the LinkedPositionalList class
In support the concept of iteration with the LinkedPositionalList class, a first question is whether to support iteration of the elements of the list or the positions of the list. If we allow a user to iterate through all positions of the list, those positions could be used to access the underlying elements, so support for position iteration is more general. However, it is more standard for a container class to support iteration of the core elements, by default, so that the for-each loop syntax could be used to write code such as the following,
for (String guest : waitlist)
assuming that variable waitlist has type LinkedPositionalList<String>.
For maximum convenience, we will support both forms of iteration. We will have the standard iterator() method return an iterator of the elements of the list, so that our list class formally implements the Iterable interface for the declared element type.
For those wishing to iterate through the positions of a list, we will provide a new method, positions(). At first glance, it would seem a natural choice for such a method to return an Iterator. However, we prefer for the return type of that method to be an instance that is Iterable (and hence, has its own iterator() method that returns an iterator of positions). Our reason for the extra layer of complexity is that we wish for users of our class to be able to use a for-each loop with a simple syntax such as the following:
for (Position<String> p : waitlist.positions())
For this syntax to be legal, the return type of positions() must be Iterable.
Code Fragment 7.14 presents our new support for the iteration of positions and elements of a LinkedPositionalList. We define three new inner classes. The first of these is PositionIterator, providing the core functionality of our list iterations. Whereas the array list iterator maintained the index of the next element to be returned as a field, this class maintains the position of the next element to be returned (as well as the position of the most recently returned element, to support removal).
To support our goal of the positions() method returning an Iterable object, we define a trivial PositionIterable inner class, which simply constructs and returns a new PositionIterator object each time its iterator() method is called. The positions() method of the top-level class returns a new PositionIterable instance. Our framework relies heavily on these being inner classes, not static nested classes.
Finally, we wish to have the top-level iterator() method return an iterator of elements (not positions). Rather than reinvent the wheel, we trivially adapt the PositionIterator class to define a new ElementIterator class, which lazily manages a position iterator instance, while returning the element stored at each position when next() is called.
Code Fragment 7.14: Support for providing iterations of positions and elements of a LinkedPositionalList. (This should be nested within the LinkedPositionalList class definition of Code Fragments 7.9–7.12.)
7.5 The Java Collections Framework
Java provides many data structure interfaces and classes, which together form the Java Collections Framework. This framework, which is part of the java.util package, includes versions of several of the data structures discussed in this book, some of which we have already discussed and others of which we will discuss later in this book. The root interface in the Java collections framework is named Collection. This is a general interface for any data structure, such as a list, that represents a collection of elements. The Collection interface includes many methods, including some we have already seen (e.g., size(), isEmpty(), iterator()). It is a superinterface for other interfaces in the Java Collections Framework that can hold elements, including the java.util interfaces Deque, List, and Queue, and other subinterfaces discussed later in this book, including Set (Section 10.5.1) and Map (Section 10.1).
The Java Collections Framework also includes concrete classes implementing various interfaces with a combination of properties and underlying representations. We summarize but a few of those classes in Table 7.3. For each, we denote which of the Queue, Deque, or List interfaces are implemented (possibly several). We also discuss several behavioral properties. Some classes enforce, or allow, a fixed capacity limit. Robust classes provide support for concurrency, allowing multiple processes to share use of a data structure in a thread-safe manner. If the structure is designated as blocking, a call to retrieve an element from an empty collection waits until some other process inserts an element. Similarly, a call to insert into a full blocking structure must wait until room becomes available.
Table 7.3: Several classes in the Java Collections Framework.
7.5.1 List Iterators in Java
The java.util.LinkedList class does not expose a position concept to users in its API, as we do in our positional list ADT. Instead, the preferred way to access and update a LinkedList object in Java, without using indices, is to use a ListIterator that is returned by the list's listIterator() method. Such an iterator provides forward and backward traversal methods as well as local update methods. It views its current position as being before the first element, between two elements, or after the last element. That is, it uses a list cursor, much like a screen cursor is viewed as being located between two characters on a screen. Specifically, the java.util.ListIterator interface includes the following methods:
| add(e): | Adds the element e at the current position of the iterator. |
| hasNext(): | Returns true if there is an element after the current position of the iterator. |
| hasPrevious(): | Returns true if there is an element before the current position of the iterator. |
| previous(): | Returns the element e before the current position and sets the current position to be before e. |
| next(): | Returns the element e after the current position and sets the current position to be after e. |
| nextIndex(): | Returns the index of the next element. |
| previousIndex(): | Returns the index of the previous element. |
| remove(): | Removes the element returned by the most recent next or previous operation. |
| set(e): | Replaces the element returned by the most recent call to the next or previous operation with e. |
It is risky to use multiple iterators over the same list while modifying its contents. If insertions, deletions, or replacements are required at multiple “places” in a list, it is safer to use positions to specify these locations. But the java.util.LinkedList class does not expose its position objects to the user. So, to avoid the risks of modifying a list that has created multiple iterators, the iterators have a “fail-fast” feature that invalidates such an iterator if its underlying collection is modified unexpectedly. For example, if a java.util.LinkedList object L has returned five different iterators and one of them modifies L, a ConcurrentModificationException is thrown if any of the other four is subsequently used. That is, Java allows many list iterators to be traversing a linked list L at the same time, but if one of them modifies L (using an add, set, or remove method), then all the other iterators for L become invalid. Likewise, if L is modified by one of its own update methods, then all existing iterators for L immediately become invalid.
7.5.2 Comparison to Our Positional List ADT
Java provides functionality similar to our array list and positional lists ADT in the java.util.List interface, which is implemented with an array in java.util.ArrayList and with a linked list in java.util.LinkedList.
Moreover, Java uses iterators to achieve a functionality similar to what our positional list ADT derives from positions. Table 7.4 shows corresponding methods between our (array and positional) list ADTs and the java.util interfaces List and ListIterator interfaces, with notes about their implementations in the java.util classes ArrayList and LinkedList.
Table 7.4: Correspondences between methods in our positional list ADT and the java.util interfaces List and ListIterator. We use A and L as abbreviations for java.util.ArrayList and java.util.LinkedList (or their running times).
7.5.3 List-Based Algorithms in the Java Collections Framework
In addition to the classes that are provided in the Java Collections Framework, there are a number of simple algorithms that it provides as well. These algorithms are implemented as static methods in the java.util.Collections class (not to be confused with the java.util.Collection interface) and they include the following methods:
| copy(Ldest, Lsrc): | Copies all elements of the Lsrc list into corresponding indices of the Ldest list. |
| disjoint(C, D): | Returns a boolean value indicating whether the collections C and D are disjoint. |
| fill(L, e): | Replaces each element of the list L with element e. |
| frequency(C, e): | Returns the number of elements in the collection C that are equal to e. |
| max(C): | Returns the maximum element in the collection C, based on the natural ordering of its elements. |
| min(C): | Returns the minimum element in the collection C, based on the natural ordering of its elements. |
| replaceAll(L, e, f): | Replaces each element in L that is equal to e with element f. |
| reverse(L): | Reverses the ordering of elements in the list L. |
| rotate(L, d): | Rotates the elements in the list L by the distance d (which can be negative), in a circular fashion. |
| shuffle(L): | Pseudorandomly permutes the ordering of the elements in the list L. |
| sort(L): | Sorts the list L, using the natural ordering of its elements. |
| swap(L, i, j): | Swap the elements at indices i and j of list L. |
Converting Lists into Arrays
Lists are a beautiful concept and they can be applied in a number of different contexts, but there are some instances where it would be useful if we could treat a list like an array. Fortunately, the java.util.Collection interface includes the following helpful methods for generating an array that has the same elements as the given collection:
| toArray(): | Returns an array of elements of type Object containing all the elements in this collection. |
| toArray(A): | Returns an array of elements of the same element type as A containing all the elements in this collection. |
If the collection is a list, then the returned array will have its elements stored in the same order as that of the original list. Thus, if we have a useful array-based method that we want to use on a list or other type of collection, then we can do so by simply using that collection's toArray() method to produce an array representation of that collection.
Converting Arrays into Lists
In a similar vein, it is often useful to be able to convert an array into an equivalent list. Fortunately, the java.util.Arrays class includes the following method:
| asList(A): | Returns a list representation of the array A, with the same element type as the elements of A. |
The list returned by this method uses the array A as its internal representation for the list. So this list is guaranteed to be an array-based list and any changes made to it will automatically be reflected in A. Because of these types of side effects, use of the asList method should always be done with caution, so as to avoid unintended consequences. But, used with care, this method can often save us a lot of work. For instance, the following code fragment could be used to randomly shuffle an array of Integer objects, arr:
Integer[ ] arr = {1, 2, 3, 4, 5, 6, 7, 8}; // allowed by autoboxing
List<Integer> listArr = Arrays.asList(arr);
Collections.shuffle(listArr); // this has side effect of shuffling arr
It is worth noting that the array A sent to the asList method should be a reference type (hence, our use of Integer rather than int in the above example). This is because the List interface is generic, and requires that the element type be an object.
7.6 Sorting a Positional List
In Section 3.1.2, we introduced the insertion-sort algorithm in the context of an array-based sequence. In this section, we develop an implementation that operates on a PositionalList, relying on the same high-level algorithm in which each element is placed relative to a growing collection of previously sorted elements.
We maintain a variable named marker that represents the rightmost position of the currently sorted portion of a list. During each pass, we consider the position just past the marker as the pivot and consider where the pivot's element belongs relative to the sorted portion; we use another variable, named walk, to move leftward from the marker, as long as there remains a preceding element with value larger than the pivot's. A typical configuration of these variables is diagrammed in Figure 7.9. A Java implementation of this strategy is given in Code 7.15.
Figure 7.9: Overview of one step of our insertion-sort algorithm. The shaded elements, those up to and including marker, have already been sorted. In this step, the pivot's element should be relocated immediately before the walk position.
Code Fragment 7.15: Java code for performing insertion-sort on a positional list.
7.7 Case Study: Maintaining Access Frequencies
The positional list ADT is useful in a number of settings. For example, a program that simulates a game of cards could model each person's hand as a positional list (Exercise P-7.60). Since most people keep cards of the same suit together, inserting and removing cards from a person's hand could be implemented using the methods of the positional list ADT, with the positions being determined by a natural order of the suits. Likewise, a simple text editor embeds the notion of positional insertion and deletion, since such editors typically perform all updates relative to a cursor, which represents the current position in the list of characters of text being edited.
In this section, we will consider maintaining a collection of elements while keeping track of the number of times each element is accessed. Keeping such access counts allows us to know which elements are among the most popular. Examples of such scenarios include a Web browser that keeps track of a user's most accessed pages, or a music collection that maintains a list of the most frequently played songs for a user. We will model this with a new favorites list ADT that supports the size and isEmpty methods as well as the following:
| access(e): | Accesses the element e, adding it to the favorites list if it is not already present, and increments its access count. |
| remove(e): | Removes element e from the favorites list, if present. |
| getFavorites(k): | Returns an iterable collection of the k most accessed elements. |
7.7.1 Using a Sorted List
Our first approach for managing a list of favorites is to store elements in a linked list, keeping them in nonincreasing order of access counts. We access or remove an element by searching the list from the most frequently accessed to the least frequently accessed. Reporting the k most accessed elements is easy, as they are the first k entries of the list.
To maintain the invariant that elements are stored in nonincreasing order of access counts, we must consider how a single access operation may affect the order. The accessed element's count increases by one, and so it may become larger than one or more of its preceding neighbors in the list, thereby violating the invariant.
Fortunately, we can reestablish the sorted invariant using a technique similar to a single pass of the insertion-sort algorithm, introduced in the previous section. We can perform a backward traversal of the list, starting at the position of the element whose access count has increased, until we locate a valid position after which the element can be relocated.
Using the Composition Pattern
We wish to implement a favorites list by making use of a PositionalList for storage. If elements of the positional list were simply elements of the favorites list, we would be challenged to maintain access counts and to keep the proper count with the associated element as the contents of the list are reordered. We use a general object-oriented design pattern, the composition pattern, in which we define a single object that is composed of two or more other objects. (See, for example, Section 2.5.2.)
Specifically, we define a nonpublic nested class, Item, that stores the element and its access count as a single instance. We then maintain our favorites list as a PositionalList of item instances, so that the access count for a user's element is embedded alongside it in our representation. (An Item is never exposed to a user of a FavoritesList.)
Code Fragment 7.16: Class FavoritesList. (Continues in Code Fragment 7.17.)
Code Fragment 7.17: Class FavoritesList. (Continued from Code Fragment 7.16.)
7.7.2 Using a List with the Move-to-Front Heuristic
The previous implementation of a favorites list performs the access(e) method in time proportional to the index of e in the favorites list. That is, if e is the kth most popular element in the favorites list, then accessing it takes O(k) time. In many real-life access sequences (e.g., Web pages visited by a user), once an element is accessed it is more likely to be accessed again in the near future. Such scenarios are said to possess locality of reference.
A heuristic, or rule of thumb, that attempts to take advantage of the locality of reference that is present in an access sequence is the move-to-front heuristic. To apply this heuristic, each time we access an element we move it all the way to the front of the list. Our hope, of course, is that this element will be accessed again in the near future. Consider, for example, a scenario in which we have n elements and the following series of n2 accesses:
- element 1 is accessed n times.
- element 2 is accessed n times.
- ...
- element n is accessed n times.
If we store the elements sorted by their access counts, inserting each element the first time it is accessed, then
- each access to element 1 runs in O(1) time.
- each access to element 2 runs in O(2) time.
- ...
- each access to element n runs in O(n) time.
Thus, the total time for performing the series of accesses is proportional to
![]()
which is O(n3).
On the other hand, if we use the move-to-front heuristic, inserting each element the first time it is accessed, then
- each subsequent access to element 1 takes O(1) time.
- each subsequent access to element 2 takes O(1) time.
- ...
- each subsequent access to element n runs in O(1) time.
So the running time for performing all the accesses in this case is O(n2). Thus, the move-to-front implementation has faster access times for this scenario. Still, the move-to-front approach is just a heuristic, for there are access sequences where using the move-to-front approach is slower than simply keeping the favorites list ordered by access counts.
The Trade-Offs with the Move-to-Front Heuristic
If we no longer maintain the elements of the favorites list ordered by their access counts, when we are asked to find the k most accessed elements, we need to search for them. We will implement the getFavorites(k) method as follows:
- We copy all entries of our favorites list into another list, named temp.
- We scan the temp list k times. In each scan, we find the entry with the largest access count, remove this entry from temp, and add it to the results.
This implementation of method getFavorites(k) takes O(kn) time. Thus, when k is a constant, method getFavorites(k) runs in O(n) time. This occurs, for example, when we want to get the “top ten” list. However, if k is proportional to n, then the method getFavorites(k) runs in O(n2) time. This occurs, for example, when we want a “top 25%” list.
In Chapter 9 we will introduce a data structure that will allow us to implement getFavorites in O(n + klogn) time (see Exercise P-9.51), and more advanced techniques could be used to perform getFavorites in O(n + klog k) time.
We could easily achieve O(nlogn) time if we use a standard sorting algorithm to reorder the temporary list before reporting the top k (see Chapter 12); this approach would be preferred to the original in the case that k is Ω(log n). (Recall the big-Omega notation introduced in Section 4.3.1 to give an asymptotic lower bound on the running time of an algorithm.) There is a specialized sorting algorithm (see Section 12.3.2) that can take advantage of the fact that access counts are integers in order to achieve O(n) time for getFavorites, for any value of k.
Implementing the Move-to-Front Heuristic in Java
We give an implementation of a favorites list using the move-to-front heuristic in Code Fragment 7.18. The new FavoritesListMTF class inherits most of its functionality from the original FavoritesList as a base class.
By our original design, the access method of the original class relies on a protected utility named moveUp to enact the potential shifting of an element forward in the list, after its access count had been incremented. Therefore, we implement the move-to-front heuristic by simply overriding the moveUp method so that each accessed element is moved directly to the front of the list (if not already there). This action is easily implemented by means of the positional list ADT.
The more complex portion of our FavoritesListMTF class is the new definition for the getFavorites method. We rely on the first of the approaches outlined above, inserting copies of the items into a temporary list and then repeatedly finding, reporting, and removing an element that has the largest access count of those remaining.
Code Fragment 7.18: Class FavoritesListMTF implementing the move-to-front heuristic. This class extends FavoritesList (Code Fragments 7.16 and 7.17) and overrides methods moveUp and getFavorites.
7.8 Exercises
Reinforcement
| R-7.1 | Draw a representation, akin to Example 7.1, of an initially empty list L after performing the following sequence of operations: add(0, 4), add(0, 3), add(0, 2), add(2, 1), add(1, 5), add(1, 6), add(3, 7), add(0, 8). |
| R-7.2 | Give an implementation of the stack ADT using an array list for storage. |
| R-7.3 | Give an implementation of the deque ADT using an array list for storage. |
| R-7.4 | Give a justification of the running times shown in Table 7.1 for the methods of an array list implemented with a (nonexpanding) array. |
| R-7.5 | The java.util.ArrayList includes a method, trimToSize(), that replaces the underlying array with one whose capacity precisely equals the number of elements currently in the list. Implement such a method for our dynamic version of the ArrayList class from Section 7.2. |
| R-7.6 | Redo the justification of Proposition 7.2 assuming that the the cost of growing the array from size k to size 2k is 3k cyber-dollars. How much should each push operation be charged to make the amortization work? |
| R-7.7 | Consider an implementation of the array list ADT using a dynamic array, but instead of copying the elements into an array of double the size (that is, from N to 2N) when its capacity is reached, we copy the elements into an array with |
| R-7.8 | Suppose we are maintaining a collection C of elements such that, each time we add a new element to the collection, we copy the contents of C into a new array list of just the right size. What is the running time of adding n elements to an initially empty collection C in this case? |
| R-7.9 | The add method for a dynamic array, as described in Code Fragment 7.5, has the following inefficiency. In the case when a resize occurs, the resize operation takes time to copy all the elements from the old array to a new array, and then the subsequent loop in the body of add shifts some of them to make room for a new element. Give an improved implementation of the add method, so that, in the case of a resize, the elements are copied into their final place in the new array (that is, no shifting is done). |
| R-7.10 | Reimplement the ArrayStack class, from Section 6.1.2, using dynamic arrays to support unlimited capacity. |
| R-7.11 | Describe an implementation of the positional list methods addLast and addBefore realized by using only methods in the set {isEmpty, first, last, before, after, addAfter, addFirst}. |
| R-7.12 | Suppose we want to extend the PositionalList abstract data type with a method, indexOf(p), that returns the current index of the element stored at position p. Show how to implement this method using only other methods of the Positional-List interface (not details of our LinkedPositionalList implementation). |
| R-7.13 | Suppose we want to extend the PositionalList abstract data type with a method, findPosition(e), that returns the first position containing an element equal to e (or null if no such position exists). Show how to implement this method using only existing methods of the PositionalList interface (not details of our LinkedPositionalList implementation). |
| R-7.14 | The LinkedPositionalList implementation of Code Fragments 7.9–7.12 does not do any error checking to test if a given position p is actually a member of the relevant list. Give a detailed explanation of the effect of a call L.addAfter(p, e) on a list L, yet with a position p that belongs to some other list M. |
| R-7.15 | To better model a FIFO queue in which entries may be deleted before reaching the front, design a LinkedPositionalQueue class that supports the complete queue ADT, yet with enqueue returning a position instance and support for a new method, remove(p), that removes the element associated with position p from the queue. You may use the adapter design pattern (Section 6.1.3), using a LinkedPositionalList as your storage. |
| R-7.16 | Describe how to implement a method, alternateIterator(), for a positional list that returns an iterator that reports only those elements having even index in the list. |
| R-7.17 | Redesign the Progression class, from Section 2.2.3, so that it formally implements the Iterator<long> interface. |
| R-7.18 | The java.util.Collection interface includes a method, contains(o), that returns true if the collection contains any object that equals Object o. Implement such a method in the ArrayList class of Section 7.2. |
| R-7.19 | The java.util.Collection interface includes a method, clear(), that removes all elements from a collection. Implement such a method in the ArrayList class of Section 7.2. |
| R-7.20 | Demonstrate how to use the java.util.Colletions.reverse method to reverse an array of objects. |
| R-7.21 | Given the set of element {a, b, c, d, e, f} stored in a list, show the final state of the list, assuming we use the move-to-front heuristic and access the elements according to the following sequence: (a, b, c, d, e, f, a, c, f, b, d, e). |
| R-7.22 | Suppose that we have made kn total accesses to the elements in a list L of n elements, for some integer k ≥ 1. What are the minimum and maximum number of elements that have been accessed fewer than k times? |
| R-7.23 | Let L be a list of n items maintained according to the move-to-front heuristic. Describe a series of O(n) accesses that will reverse L. |
| R-7.24 | Implement a resetCounts() method for the FavoritesList class that resets all elements' access counts to zero (while leaving the order of the list unchanged). |
Creativity
| C-7.25 | Give an array-based list implementation, with fixed capacity, treating the array circularly so that it achieves O(1) time for insertions and removals at index 0, as well as insertions and removals at the end of the array list. Your implementation should also provide for a constant-time get method. |
| C-7.26 | Complete the previous exercise, except using a dynamic array to provide unbounded capacity. |
| C-7.27 | Modify our ArrayList implementation to support the Cloneable interface, as described in Section 3.6. |
| C-7.28 | In Section 7.5.3, we demonstrated how the Collections.shuffle method can be adapted to shuffle a reference-type array. Give a direct implementation of a shuffle method for an array of int values. You may use the method, nextInt(n) of the Random class, which returns a random number between 0 and n − 1, inclusive. Your method should guarantee that every possible ordering is equally likely. What is the running time of your method? |
| C-7.29 | Revise the array list implementation given in Section 7.2.1 so that when the actual number of elements, n, in the array goes below N/4, where N is the array capacity, the array shrinks to half its size. |
| C-7.30 | Prove that when using a dynamic array that grows and shrinks as in the previous exercise, the following series of 2n operations takes O(n) time: n insertions at the end of an initially empty list, followed by n deletions, each from the end of the list. |
| C-7.31 | Give a formal proof that any sequence of n push or pop operations (that is, insertions or deletions at the end) on an initially empty dynamic array takes O(n) time, if using the strategy described in Exercise C-7.29. |
| C-7.32 | Consider a variant of Exercise C-7.29, in which an array of capacity N is resized to capacity precisely that of the number of elements, any time the number of elements in the array goes strictly below N/4. Give a formal proof that any sequence of n push or pop operations on an initially empty dynamic array takes O(n) time. |
| C-7.33 | Consider a variant of Exercise C-7.29, in which an array of capacity N, is resized to capacity precisely that of the number of elements, any time the number of elements in the array goes strictly below N/2. Show that there exists a sequence of n push and pop operations that requires Ω(n2) time to execute. |
| C-7.34 | Describe how to implement the queue ADT using two stacks as instance variables, such that all queue operations execute in amortized O(1) time. Give a formal proof of the amortized bound. |
| C-7.35 | Reimplement the ArrayQueue class, from Section 6.2.2, using dynamic arrays to support unlimited capacity. Be especially careful about the treatment of a circular array when resizing. |
| C-7.36 | Suppose we want to extend the PositionalList interface to include a method, positionAtIndex(i), that returns the position of the element having index i (or throws an IndexOutOfBoundsException, if warranted). Show how to implement this method, using only existing methods of the PositionalList interface, by traversing the appropriate number of steps from the front of the list. |
| C-7.37 | Repeat the previous problem, but use knowledge of the size of the list to traverse from the end of the list that is closest to the desired index. |
| C-7.38 | Explain how any implementation of the PositionalList ADT can be made to support all methods of the List ADT, described in Section 7.1, assuming an implementation is given for the positionAtIndex(i) method, proposed in Exercise C-7.36. |
| C-7.39 | Suppose we want to extend the PositionalList abstract data type with a method, moveToFront(p), that moves the element at position p to the front of a list (if not already there), while keeping the relative order of the remaining elements unchanged. Show how to implement this method using only existing methods of the PositionalList interface (not details of our LinkedPositionalList implementation). |
| C-7.40 | Redo the previous problem, but providing an implementation within the class LinkedPositionalList that does not create or destroy any nodes. |
| C-7.41 | Modify our LinkedPositionalList implementation to support the Cloneable interface, as described in Section 3.6. |
| C-7.42 | Describe a nonrecursive method for reversing a positional list represented with a doubly linked list using a single pass through the list. |
| C-7.43 | Page 281 describes an array-based representation for implementing the positional list ADT. Give a pseudocode description of the addBefore method for that representation. |
| C-7.44 | Describe a method for performing a card shuffle of a list of 2n elements, by converting it into two lists. A card shuffle is a permutation where a list L is cut into two lists, L1 and L2, where L1 is the first half of L and L2 is the second half of L, and then these two lists are merged into one by taking the first element in L1, then the first element in L2, followed by the second element in L1, the second element in L2, and so on. |
| C-7.45 | How might the LinkedPositionalList class be redesigned to detect the error described in Exercise R-7.14. |
| C-7.46 | Modify the LinkedPositionalList class to support a method swap(p, q) that causes the underlying nodes referenced by positions p and q to be exchanged for each other. Relink the existing nodes; do not create any new nodes. |
| C-7.47 | An array is sparse if most of its entries are null. A list L can be used to implement such an array, A, efficiently. In particular, for each nonnull cell A[i], we can store a pair (i, e) in L, where e is the element stored at A[i]. This approach allows us to represent A using O(m) storage, where m is the number of nonnull entries in A. Describe and analyze efficient ways of performing the methods of the array list ADT on such a representation. |
| C-7.48 | Design a circular positional list ADT that abstracts a circularly linked list in the same way that the positional list ADT abstracts a doubly linked list. |
| C-7.49 | Provide an implementation of the listiterator() method, in the context of the class LinkedPositionalList, that returns an object that supports the java.util.ListIterator interface described in Section 7.5.1. |
| C-7.50 | Describe a scheme for creating list iterators that fail fast, that is, they all become invalid as soon as the underlying list changes. |
| C-7.51 | There is a simple algorithm, called bubble-sort, for sorting a list L of n comparable elements. This algorithm scans the list n − 1 times, where, in each scan, the algorithm compares the current element with the next one and swaps them if they are out of order. Give a pseudocode description of bubble-sort that is as efficient as possible assuming L is implemented with a doubly linked list. What is the running time of this algorithm? |
| C-7.52 | Redo Exercise C-7.51 assuming L is implemented with an array list. |
| C-7.53 | Describe an efficient method for maintaining a favorites list L, with the move-to-front heuristic, such that elements that have not been accessed in the most recent n accesses are automatically purged from the list. |
| C-7.54 | Suppose we have an n-element list L maintained according to the move-to-front heuristic. Describe a sequence of n2 accesses that is guaranteed to take Ω(n3) time to perform on L. |
| C-7.55 | A useful operation in databases is the natural join. If we view a database as a list of ordered pairs of objects, then the natural join of databases A and B is the list of all ordered triples (x, y, z) such that the pair (x, y) is in A and the pair (y, z) is in B. Describe and analyze an efficient algorithm for computing the natural join of a list A of n pairs and a list B of m pairs. |
| C-7.56 | When Bob wants to send Alice a message M on the Internet, he breaks M into n data packets, numbers the packets consecutively, and injects them into the network. When the packets arrive at Alice's computer, they may be out of order, so Alice must assemble the sequence of n packets in order before she can be sure she has the entire message. Describe an efficient scheme for Alice to do this. What is the running time of this algorithm? |
| C-7.57 | Implement the FavoritesList class using an array list. |
Projects
| P-7.58 | Develop an experiment, using techniques similar to those in Section 4.1, to test the efficiency of n successive calls to the add method of an ArrayList, for various n, under each of the following three scenarios:
Analyze your empirical results. |
| P-7.59 | Reimplement the LinkedPositionalList class so that an invalid position is reported in a scenario such as the one described in Exercise R-7.14. |
| P-7.60 | Implement a CardHand class that supports a person arranging a group of cards in his or her hand. The simulator should represent the sequence of cards using a single positional list ADT so that cards of the same suit are kept together. Implement this strategy by means of four “fingers” into the hand, one for each of the suits of hearts, clubs, spades, and diamonds, so that adding a new card to the person's hand or playing a correct card from the hand can be done in constant time. The class should support the following methods:
|
| P-7.61 | Write a simple text editor, which stores and displays a string of characters using the positional list ADT, together with a cursor object that highlights a position in the string. The editor must support the following operations:
|
Chapter Notes
The treatment of data structures as collections (and other principles of object-oriented design) can be found in object-oriented design books by Booch [16], Budd [19], and Liskov and Guttag [67]. Lists and iterators are pervasive concepts in the Java Collections Framework. Our positional list ADT is derived from the “position” abstraction introduced by Aho, Hopcroft, and Ullman [6], and the list ADT of Wood [96]. Implementations of lists via arrays and linked lists are discussed by Knuth [60].