Chapter
6
Stacks, Queues, and Deques

Contents
6.1.1 The Stack Abstract Data Type
6.1.2 A Simple Array-Based Stack Implementation
6.1.3 Implementing a Stack with a Singly Linked List
6.1.4 Reversing an Array Using a Stack
6.1.5 Matching Parentheses and HTML Tags
6.2.1 The Queue Abstract Data Type
6.2.2 Array-Based Queue Implementation
6.2.3 Implementing a Queue with a Singly Linked List
6.3.1 The Deque Abstract Data Type
6.1 Stacks
A stack is a collection of objects that are inserted and removed according to the last-in, first-out (LIFO) principle. A user may insert objects into a stack at any time, but may only access or remove the most recently inserted object that remains (at the so-called “top” of the stack). The name “stack” is derived from the metaphor of a stack of plates in a spring-loaded, cafeteria plate dispenser. In this case, the fundamental operations involve the “pushing” and “popping” of plates on the stack. When we need a new plate from the dispenser, we “pop” the top plate off the stack, and when we add a plate, we “push” it down on the stack to become the new top plate. Perhaps an even more amusing example is a PEZ® candy dispenser, which stores mint candies in a spring-loaded container that “pops” out the topmost candy in the stack when the top of the dispenser is lifted (see Figure 6.1).
Figure 6.1: A schematic drawing of a PEZ® dispenser; a physical implementation of the stack ADT. (PEZ® is a registered trademark of PEZ Candy, Inc.)
Stacks are a fundamental data structure. They are used in many applications, including the following.
Example 6.1: Internet Web browsers store the addresses of recently visited sites on a stack. Each time a user visits a new site, that site's address is “pushed” onto the stack of addresses. The browser then allows the user to “pop” back to previously visited sites using the “back” button.
Example 6.2: Text editors usually provide an “undo” mechanism that cancels recent editing operations and reverts to former states of a document. This undo operation can be accomplished by keeping text changes in a stack.
6.1.1 The Stack Abstract Data Type
Stacks are the simplest of all data structures, yet they are also among the most important, as they are used in a host of different applications, and as a tool for many more sophisticated data structures and algorithms. Formally, a stack is an abstract data type (ADT) that supports the following two update methods:
| push(e): | Adds element e to the top of the stack. |
| pop(): | Removes and returns the top element from the stack (or null if the stack is empty). |
Additionally, a stack supports the following accessor methods for convenience:
| top(): | Returns the top element of the stack, without removing it (or null if the stack is empty). |
| size(): | Returns the number of elements in the stack. |
| isEmpty(): | Returns a boolean indicating whether the stack is empty. |
By convention, we assume that elements added to the stack can have arbitrary type and that a newly created stack is empty.
Example 6.3: The following table shows a series of stack operations and their effects on an initially empty stack S of integers.

A Stack Interface in Java
In order to formalize our abstraction of a stack, we define what is known as its application programming interface (API) in the form of a Java interface, which describes the names of the methods that the ADT supports and how they are to be declared and used. This interface is defined in Code Fragment 6.1.
We rely on Java's generics framework (described in Section 2.5.2), allowing the elements stored in the stack to belong to any object type <E>. For example, a variable representing a stack of integers could be declared with type Stack<Integer>. The formal type parameter is used as the parameter type for the push method, and the return type for both pop and top.
Recall, from the discussion of Java interfaces in Section 2.3.1, that the interface serves as a type definition but that it cannot be directly instantiated. For the ADT to be of any use, we must provide one or more concrete classes that implement the methods of the interface associated with that ADT. In the following subsections, we will give two such implementations of the Stack interface: one that uses an array for storage and another that uses a linked list.
The java.util.Stack Class
Because of the importance of the stack ADT, Java has included, since its original version, a concrete class named java.util.Stack that implements the LIFO semantics of a stack. However, Java's Stack class remains only for historic reasons, and its interface is not consistent with most other data structures in the Java library. In fact, the current documentation for the Stack class recommends that it not be used, as LIFO functionality (and more) is provided by a more general data structure known as a double-ended queue (which we describe in Section 6.3).
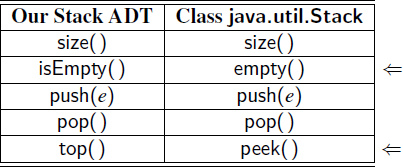
For the sake of comparison, Table 6.1 provides a side-by-side comparison of the interface for our stack ADT and the java.util.Stack class. In addition to some differences in method names, we note that methods pop and peek of the java.util.Stack class throw a custom EmptyStackException if called when the stack is empty (whereas null is returned in our abstraction).
Table 6.1: Methods of our stack ADT and corresponding methods of the class java.util.Stack, with differences highlighted in the right margin.
Code Fragment 6.1: Interface Stack documented with comments in Javadoc style (Section 1.9.4). Note also the use of the generic parameterized type, E, which allows a stack to contain elements of any specified (reference) type.
6.1.2 A Simple Array-Based Stack Implementation
As our first implementation of the stack ADT, we store elements in an array, named data, with capacity N for some fixed N. We oriented the stack so that the bottom element of the stack is always stored in cell data[0], and the top element of the stack in cell data[t] for index t that is equal to one less than the current size of the stack. (See Figure 6.2.)
Figure 6.2: Representing a stack with an array; the top element is in cell data[t].
Recalling that arrays start at index 0 in Java, when the stack holds elements from data[0] to data[t] inclusive, it has size t + 1. By convention, when the stack is empty it will have t equal to −1 (and thus has size t + 1, which is 0). A complete Java implementation based on this strategy is given in Code Fragment 6.2 (with Javadoc comments omitted due to space considerations).
Code Fragment 6.2: Array-based implementation of the Stack interface.
A Drawback of This Array-Based Stack Implementation
The array implementation of a stack is simple and efficient. Nevertheless, this implementation has one negative aspect—it relies on a fixed-capacity array, which limits the ultimate size of the stack.
For convenience, we allow the user of a stack to specify the capacity as a parameter to the constructor (and offer a default constructor that uses capacity of 1,000). In cases where a user has a good estimate on the number of items needing to go in the stack, the array-based implementation is hard to beat. However, if the estimate is wrong, there can be grave consequences. If the application needs much less space than the reserved capacity, memory is wasted. Worse yet, if an attempt is made to push an item onto a stack that has already reached its maximum capacity, the implementation of Code Fragment 6.2 throws an IllegalStateException, refusing to store the new element. Thus, even with its simplicity and efficiency, the array-based stack implementation is not necessarily ideal.
Fortunately, we will later demonstrate two approaches for implementing a stack without such a size limitation and with space always proportional to the actual number of elements stored in the stack. One approach, given in the next subsection uses a singly linked list for storage; in Section 7.2.1, we will provide a more advanced array-based approach that overcomes the limit of a fixed capacity.
Analyzing the Array-Based Stack Implementation
The correctness of the methods in the array-based implementation follows from our definition of index t. Note well that when pushing an element, t is incremented before placing the new element, so that it uses the first available cell.
Table 6.2 shows the running times for methods of this array-based stack implementation. Each method executes a constant number of statements involving arithmetic operations, comparisons, and assignments, or calls to size and isEmpty, which both run in constant time. Thus, in this implementation of the stack ADT, each method runs in constant time, that is, they each run in O(1) time.
| Method | Running Time |
| size | O(1) |
| isEmpty | O(1) |
| top | O(1) |
| push | O(1) |
| pop | O(1) |
Table 6.2: Performance of a stack realized by an array. The space usage is O(N), where N is the size of the array, determined at the time the stack is instantiated, and independent from the number n ≤ N of elements that are actually in the stack.
Garbage Collection in Java
We wish to draw attention to one interesting aspect involving the implementation of the pop method in Code Fragment 6.2. We set a local variable, answer, to reference the element that is being popped, and then we intentionally reset data[t] to null at line 22, before decrementing t. The assignment to null was not technically required, as our stack would still operate correctly without it.
Our reason for returning the cell to a null reference is to assist Java's garbage collection mechanism, which searches memory for objects that are no longer actively referenced and reclaims their space for future use. (For more details, see Section 15.1.3.) If we continued to store a reference to the popped element in our array, the stack class would ignore it (eventually overwriting the reference if more elements get added to the stack). But, if there were no other active references to the element in the user's application, that spurious reference in the stack's array would stop Java's garbage collector from reclaiming the element.
Sample Usage
We conclude this section by providing a demonstration of code that creates and uses an instance of the ArrayStack class. In this example, we declare the parameterized type of the stack as the Integer wrapper class. This causes the signature of the push method to accept an Integer instance as a parameter, and for the return type of both top and pop to be an Integer. Of course, with Java's autoboxing and unboxing (see Section 1.3), a primitive int can be sent as a parameter to push.
Code Fragment 6.3: Sample usage of our ArrayStack class.
6.1.3 Implementing a Stack with a Singly Linked List
In this section, we demonstrate how the Stack interface can be easily implemented using a singly linked list for storage. Unlike our array-based implementation, the linked-list approach has memory usage that is always proportional to the number of actual elements currently in the stack, and without an arbitrary capacity limit.
In designing such an implementation, we need to decide if the top of the stack is at the front or back of the list. There is clearly a best choice here, however, since we can insert and delete elements in constant time only at the front. With the top of the stack stored at the front of the list, all methods execute in constant time.
The Adapter Pattern
The adapter design pattern applies to any context where we effectively want to modify an existing class so that its methods match those of a related, but different, class or interface. One general way to apply the adapter pattern is to define a new class in such a way that it contains an instance of the existing class as a hidden field, and then to implement each method of the new class using methods of this hidden instance variable. By applying the adapter pattern in this way, we have created a new class that performs some of the same functions as an existing class, but repackaged in a more convenient way.
In the context of the stack ADT, we can adapt our SinglyLinkedList class of Section 3.2.1 to define a new LinkedStack class, shown in Code Fragment 6.4. This class declares a SinglyLinkedList named list as a private field, and uses the following correspondences:
| Stack Method | Singly Linked List Method |
| size() | list.size() |
| isEmpty() | list.isEmpty() |
| push(e) | list.addFirst(e) |
| pop() | list.removeFirst() |
| top() | list.first() |
Code Fragment 6.4: Implementation of a Stack using a SinglyLinkedList as storage.
6.1.4 Reversing an Array Using a Stack
As a consequence of the LIFO protocol, a stack can be used as a general toll to reverse a data sequence. For example, if the values 1, 2, and 3 are pushed onto a stack in that order, they will be popped from the stack in the order 3, 2, and then 1.
We demonstrate this concept by revisiting the problem of reversing the elements of an array. (We provided a recursive algorithm for this task in Section 5.3.1.) We create an empty stack for auxiliary storage, push all of the array elements onto the stack, and then pop those elements off of the stack while overwriting the cells of the array from beginning to end. In Code Fragment 6.5, we give a Java implementation of this algorithm. We show an example use of this method in Code Fragment 6.6.
Code Fragment 6.5: A generic method that reverses the elements in an array with objects of type E, using a stack declared with the interface Stack<E> as its type.
1 /** Tester routine for reversing arrays */ 2 public static void main(String args[ ]) { 3 Integer[ ] a = {4, 8, 15, 16, 23, 42}; // autoboxing allows this 4 String[ ] s = {"Jack", "Kate", "Hurley", "Jin", "Michael"}; 5 System.out.println("a = " + Arrays.toString(a)); 6 System.out.println("s = " + Arrays.toString(s)); 7 System.out.println("Reversing..."); 8 reverse(a); 9 reverse(s); 10 System.out.println("a = " + Arrays.toString(a)); 11 System.out.println("s = " + Arrays.toString(s)); 12 }
The output from this method is the following:
Code Fragment 6.6: A test of the reverse method using two arrays.
6.1.5 Matching Parentheses and HTML Tags
In this subsection, we explore two related applications of stacks, both of which involve testing for pairs of matching delimiters. In our first application, we consider arithmetic expressions that may contain various pairs of grouping symbols, such as
- Parentheses: “(” and “)”
- Braces: “{” and “}”
- Brackets: “[” and “]”
Each opening symbol must match its corresponding closing symbol. For example, a left bracket, “[,” must match a corresponding right bracket, “],” as in the following expression
[(5 + x) − (y + z)].
The following examples further illustrate this concept:
- Correct: ()(()){([()])}
- Correct: ((()(()){([()])}))
- Incorrect: )(()){([()])}
- Incorrect: ({[ ])}
- Incorrect: (
We leave the precise definition of a matching group of symbols to Exercise R-6.6.
An Algorithm for Matching Delimiters
An important task when processing arithmetic expressions is to make sure their delimiting symbols match up correctly. We can use a stack to perform this task with a single left-to-right scan of the original string.
Each time we encounter an opening symbol, we push that symbol onto the stack, and each time we encounter a closing symbol, we pop a symbol from the stack (assuming it is not empty) and check that these two symbols form a valid pair. If we reach the end of the expression and the stack is empty, then the original expression was properly matched. Otherwise, there must be an opening delimiter on the stack without a matching symbol. If the length of the original expression is n, the algorithm will make at most n calls to push and n calls to pop. Code Fragment 6.7 presents a Java implementation of such an algorithm. It specifically checks for delimiter pairs (), { }, and [ ], but could easily be changed to accommodate further symbols. Specifically, we define two fixed strings, "({[" and ")}]", that are intentionally coordinated to reflect the symbol pairs. When examining a character of the expression string, we call the indexOf method of the String class on these special strings to determine if the character matches a delimiter and, if so, which one. Method indexOf returns the the index at which a given character is first found in a string (or −1 if the character is not found).
Code Fragment 6.7: Method for matching delimiters in an arithmetic expression.
Matching Tags in a Markup Language
Another application of matching delimiters is in the validation of markup languages such as HTML or XML. HTML is the standard format for hyperlinked documents on the Internet and XML is an extensible markup language used for a variety of structured data sets. We show a sample HTML document in Figure 6.3.
Figure 6.3: Illustrating (a) an HTML document and (b) its rendering.
In an HTML document, portions of text are delimited by HTML tags. A simple opening HTML tag has the form “<name>” and the corresponding closing tag has the form “</name>”. For example, we see the <body> tag on the first line of Figure 6.3a, and the matching </body> tag at the close of that document. Other commonly used HTML tags that are used in this example include:
- <body>: document body
- <h1>: section header
- <center>: center justify
- <p>: paragraph
- <ol>: numbered (ordered) list
- <li>: list item
Ideally, an HTML document should have matching tags, although most browsers tolerate a certain number of mismatching tags. In Code Fragment 6.8, we give a Java method that matches tags in a string representing an HTML document.
We make a left-to-right pass through the raw string, using index j to track our progress. The indexOf method of the String class, which optionally accepts a starting index as a second parameter, locates the '<' and '>' characters that define the tags. Method substring, also of the String class, returns the substring starting at a given index and optionally ending right before another given index. Opening tags are pushed onto the stack, and matched against closing tags as they are popped from the stack, just as we did when matching delimiters in Code Fragment 6.7.
Code Fragment 6.8: Method for testing if an HTML document has matching tags.
6.2 Queues
Another fundamental data structure is the queue. It is a close “cousin” of the stack, but a queue is a collection of objects that are inserted and removed according to the first-in, first-out (FIFO) principle. That is, elements can be inserted at any time, but only the element that has been in the queue the longest can be next removed.
We usually say that elements enter a queue at the back and are removed from the front. A metaphor for this terminology is a line of people waiting to get on an amusement park ride. People waiting for such a ride enter at the back of the line and get on the ride from the front of the line. There are many other applications of queues (see Figure 6.4). Stores, theaters, reservation centers, and other similar services typically process customer requests according to the FIFO principle. A queue would therefore be a logical choice for a data structure to handle calls to a customer service center, or a wait-list at a restaurant. FIFO queues are also used by many computing devices, such as a networked printer, or a Web server responding to requests.
Figure 6.4: Real-world examples of a first-in, first-out queue. (a) People waiting in line to purchase tickets; (b) phone calls being routed to a customer service center.
6.2.1 The Queue Abstract Data Type
Formally, the queue abstract data type defines a collection that keeps objects in a sequence, where element access and deletion are restricted to the first element in the queue, and element insertion is restricted to the back of the sequence. This restriction enforces the rule that items are inserted and deleted in a queue according to the first-in, first-out (FIFO) principle. The queue abstract data type (ADT) supports the following two update methods:
| enqueue(e): | Adds element e to the back of queue. |
| dequeue(): | Removes and returns the first element from the queue (or null if the queue is empty). |
The queue ADT also includes the following accessor methods (with first being analogous to the stack's top method):
| first(): | Returns the first element of the queue, without removing it (or null if the queue is empty). |
| size(): | Returns the number of elements in the queue. |
| isEmpty(): | Returns a boolean indicating whether the queue is empty. |
By convention, we assume that elements added to the queue can have arbitrary type and that a newly created queue is empty. We formalize the queue ADT with the Java interface shown in Code Fragment 6.9.
Code Fragment 6.9: A Queue interface defining the queue ADT, with a standard FIFO protocol for insertions and removals.
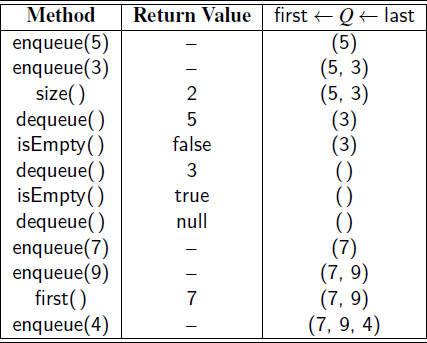
Example 6.4: The following table shows a series of queue operations and their effects on an initially empty queue Q of integers.
The java.util.Queue Interface in Java
Java provides a type of queue interface, java.util.Queue, which has functionality similar to the traditional queue ADT, given above, but the documentation for the java.util.Queue interface does not insist that it support only the FIFO principle. When supporting the FIFO principle, the methods of the java.util.Queue interface have the equivalences with the queue ADT shown in Table 6.3.
The java.util.Queue interface supports two styles for most operations, which vary in the way that they treat exceptional cases. When a queue is empty, the remove() and element() methods throw a NoSuchElementException, while the corresponding methods poll() and peek() return null. For implementations with a bounded capacity, the add method will throw an IllegalStateException when full, while the offer method ignores the new element and returns false to signal that the element was not accepted.
Table 6.3: Methods of the queue ADT and corresponding methods of the interface java.util.Queue, when supporting the FIFO principle.
6.2.2 Array-Based Queue Implementation
In Section 6.1.2, we implemented the LIFO semantics of the Stack ADT using an array (albeit, with a fixed capacity), such that every operation executes in constant time. In this section, we will consider how to use an array to efficiently support the FIFO semantics of the Queue ADT.
Let's assume that as elements are inserted into a queue, we store them in an array such that the first element is at index 0, the second element at index 1, and so on. (See Figure 6.5.)
Figure 6.5: Using an array to store elements of a queue, such that the first element inserted, “A”, is at cell 0, the second element inserted, “B”, at cell 1, and so on.
With such a convention, the question is how we should implement the dequeue operation. The element to be removed is stored at index 0 of the array. One strategy is to execute a loop to shift all other elements of the queue one cell to the left, so that the front of the queue is again aligned with cell 0 of the array. Unfortunately, the use of such a loop would result in an O(n) running time for the dequeue method.
We can improve on the above strategy by avoiding the loop entirely. We will replace a dequeued element in the array with a null reference, and maintain an explicit variable f to represent the index of the element that is currently at the front of the queue. Such an algorithm for dequeue would run in O(1) time. After several dequeue operations, this approach might lead to the configuration portrayed in Figure 6.6.
Figure 6.6: Allowing the front of the queue to drift away from index 0. In this representation, index f denotes the location of the front of the queue.
However, there remains a challenge with the revised approach. With an array of capacity N, we should be able to store up to N elements before reaching any exceptional case. If we repeatedly let the front of the queue drift rightward over time, the back of the queue would reach the end of the underlying array even when there are fewer than N elements currently in the queue. We must decide how to store additional elements in such a configuration.
Using an Array Circularly
In developing a robust queue implementation, we allow both the front and back of the queue to drift rightward, with the contents of the queue “wrapping around” the end of an array, as necessary. Assuming that the array has fixed length N, new elements are enqueued toward the “end” of the current queue, progressing from the front to index N − 1 and continuing at index 0, then 1. Figure 6.7 illustrates such a queue with first element F and last element R.
Figure 6.7: Modeling a queue with a circular array that wraps around the end.
Implementing such a circular view is relatively easy with the modulo operator, denoted with the symbol % in Java. Recall that the modulo operator is computed by taking the remainder after an integral division. For example, 14 divided by 3 has a quotient of 4 with remainder 2, that is, ![]() . So in Java, 14 / 3 evaluates to the quotient 4, while 14 % 3 evaluates to the remainder 2.
. So in Java, 14 / 3 evaluates to the quotient 4, while 14 % 3 evaluates to the remainder 2.
The modulo operator is ideal for treating an array circularly. When we dequeue an element and want to “advance” the front index, we use the arithmetic f = (f + 1) % N. As a concrete example, if we have an array of length 10, and a front index 7, we can advance the front by formally computing (7+1) % 10, which is simply 8, as 8 divided by 10 is 0 with a remainder of 8. Similarly, advancing index 8 results in index 9. But when we advance from index 9 (the last one in the array), we compute (9+1) % 10, which evaluates to index 0 (as 10 divided by 10 has a remainder of zero).
A Java Queue Implementation
A complete implementation of a queue ADT using an array in circular fashion is presented in Code Fragment 6.10. Internally, the queue class maintains the following three instance variables:
| data: | a reference to the underlying array. |
| f: | an integer that represents the index, within array data, of the first element of the queue (assuming the queue is not empty). |
| sz: | an integer representing the current number of elements stored in the queue (not to be confused with the length of the array). |
We allow the user to specify the capacity of the queue as an optional parameter to the constructor.
The implementations of methods size and isEmpty are trivial, given the sz field, and the implementation of first is simple, given index f. A discussion of update methods enqueue and dequeue follows the presentation of the code.
Code Fragment 6.10: Array-based implementation of a queue.
Adding and Removing Elements
The goal of the enqueue method is to add a new element to the back of the queue. We need to determine the proper index at which to place the new element. Although we do not explicitly maintain an instance variable for the back of the queue, we compute the index of the next opening based on the formula:
avail = (f + sz) % data.length;
Note that we are using the size of the queue as it exists prior to the addition of the new element. As a sanity check, for a queue with capacity 10, current size 3, and first element at index 5, its three elements are stored at indices 5, 6, and 7, and the next element should be added at index 8, computed as (5+3) % 10. As a case with wraparound, if the queue has capacity 10, current size 3, and first element at index 8, its three elements are stored at indices 8, 9, and 0, and the next element should be added at index 1, computed as (8+3) % 10.
When the dequeue method is called, the current value of f designates the index of the value that is to be removed and returned. We keep a local reference to the element that will be returned, before setting its cell of the array back to null, to aid the garbage collector. Then the index f is updated to reflect the removal of the first element, and the presumed promotion of the second element to become the new first. In most cases, we simply want to increment the index by one, but because of the possibility of a wraparound configuration, we rely on modular arithmetic, computing f = (f+1) % data.length, as originally described on page 242.
Analyzing the Efficiency of an Array-Based Queue
Table 6.4 shows the running times of methods in a realization of a queue by an array. As with our array-based stack implementation, each of the queue methods in the array realization executes a constant number of statements involving arithmetic operations, comparisons, and assignments. Thus, each method in this implementation runs in O(1) time.
| Method | Running Time |
| size | O(1) |
| isEmpty | O (1) |
| first | O (1) |
| enqueue | O(1) |
| dequeue | O(1) |
Table 6.4: Performance of a queue realized by an array. The space usage is O(N), where N is the size of the array, determined at the time the queue is created, and independent from the number n < N of elements that are actually in the queue.
6.2.3 Implementing a Queue with a Singly Linked List
As we did for the stack ADT, we can easily adapt a singly linked list to implement the queue ADT while supporting worst-case O(1)-time for all operations, and without any artificial limit on the capacity. The natural orientation for a queue is to align the front of the queue with the front of the list, and the back of the queue with the tail of the list, because the only update operation that singly linked lists support at the back end is an insertion. Our Java implementation of a LinkedQueue class is given in Code 6.11.
Code Fragment 6.11: Implementation of a Queue using a SinglyLinkedList.
Analyzing the Efficiency of a Linked Queue
Although we had not yet introduced asymptotic analysis when we presented our SinglyLinkedList implementation in Chapter 3, it is clear upon reexamination that each method of that class runs in O(1) worst-case time. Therefore, each method of our LinkedQueue adaptation also runs in O(1) worst-case time.
We also avoid the need to specify a maximum size for the queue, as was done in the array-based queue implementation. However, this benefit comes with some expense. Because each node stores a next reference, in addition to the element reference, a linked list uses more space per element than a properly sized array of references.
Also, although all methods execute in constant time for both implementations, it seems clear that the operations involving linked lists have a large number of primitive operations per call. For example, adding an element to an array-based queue consists primarily of calculating an index with modular arithmetic, storing the element in the array cell, and incrementing the size counter. For a linked list, an insertion includes the instantiation and initialization of a new node, relinking an existing node to the new node, and incrementing the size counter. In practice, this makes the linked-list method more expensive than the array-based method.
6.2.4 A Circular Queue
In Section 3.3, we implemented a circularly linked list class that supports all behaviors of a singly linked list, and an additional rotate() method that efficiently moves the first element to the end of the list. We can generalize the Queue interface to define a new CircularQueue interface with such a behavior, as shown in Code Fragment 6.12.
Code Fragment 6.12: A Java interface, CircularQueue, that extends the Queue ADT with a new rotate() method.
This interface can easily be implemented by adapting the CircularlyLinkedList class of Section 3.3 to produce a new LinkedCircularQueue class. This class has an advantage over the traditional LinkedQueue, because a call to Q.rotate() is implemented more efficiently than the combination of calls, Q.enqueue(Q.dequeue()), because no nodes are created, destroyed, or relinked by the implementation of a rotate operation on a circularly linked list.
A circular queue is an excellent abstraction for applications in which elements are cyclically arranged, such as for multiplayer, turn-based games, or round-robin scheduling of computing processes. In the remainder of this section, we provide a demonstration of the use of a circular queue.
The Josephus Problem
In the children's game “hot potato,” a group of n children sit in a circle passing an object, called the “potato,” around the circle. The potato begins with a starting child in the circle, and the children continue passing the potato until a leader rings a bell, at which point the child holding the potato must leave the game after handing the potato to the next child in the circle. After the selected child leaves, the other children close up the circle. This process is then continued until there is only one child remaining, who is declared the winner. If the leader always uses the strategy of ringing the bell so that every kth person is removed from the circle, for some fixed value k, then determining the winner for a given list of children is known as the Josephus problem (named after an ancient story with far more severe consequences than in the children's game).
Solving the Josephus Problem Using a Queue
We can solve the Josephus problem for a collection of n elements using a circular queue, by associating the potato with the element at the front of the queue and storing elements in the queue according to their order around the circle. Thus, passing the potato is equivalent to rotating the first element to the back of the queue. After this process has been performed k − 1 times, we remove the front element by dequeuing it from the queue and discarding it. We show a complete Java program for solving the Josephus problem using this approach in Code Fragment 6.13, which describes a solution that runs in O(nk) time. (We can solve this problem faster using techniques beyond the scope of this book.)
Code Fragment 6.13: A complete Java program for solving the Josephus problem using a circular queue.
6.3 Double-Ended Queues
We next consider a queue-like data structure that supports insertion and deletion at both the front and the back of the queue. Such a structure is called a double-ended queue, or deque, which is usually pronounced “deck” to avoid confusion with the dequeue method of the regular queue ADT, which is pronounced like the abbreviation “D.Q.”
The deque abstract data type is more general than both the stack and the queue ADTs. The extra generality can be useful in some applications. For example, we described a restaurant using a queue to maintain a waitlist. Occasionally, the first person might be removed from the queue only to find that a table was not available; typically, the restaurant will reinsert the person at the first position in the queue. It may also be that a customer at the end of the queue may grow impatient and leave the restaurant. (We will need an even more general data structure if we want to model customers leaving the queue from other positions.)
6.3.1 The Deque Abstract Data Type
The deque abstract data type is richer than both the stack and the queue ADTs. To provide a symmetrical abstraction, the deque ADT is defined to support the following update methods:
| addFirst(e): | Insert a new element e at the front of the deque. |
| addLast(e): | Insert a new element e at the back of the deque. |
| removeFirst(): | Remove and return the first element of the deque (or null if the deque is empty). |
| removeLast(): | Remove and return the last element of the deque (or null if the deque is empty). |
Additionally, the deque ADT will include the following accessors:
| first(): | Returns the first element of the deque, without removing it (or null if the deque is empty). |
| last(): | Returns the last element of the deque, without removing it (or null if the deque is empty). |
| size(): | Returns the number of elements in the deque. |
| isEmpty(): | Returns a boolean indicating whether the deque is empty. |
We formalize the deque ADT with the Java interface shown in Code Fragment 6.14.
Code Fragment 6.14: A Java interface, Deque, describing the double-ended queue ADT. Note the use of the generic parameterized type, E, allowing a deque to contain elements of any specified class.
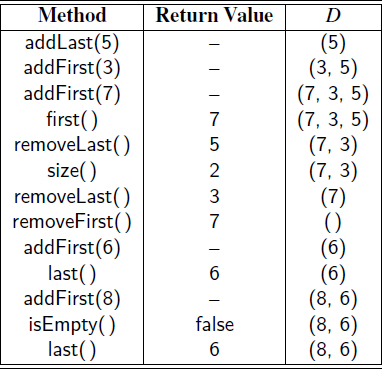
Example 6.5: The following table shows a series of operations and their effects on an initially empty deque D of integers.
6.3.2 Implementing a Deque
We can implement the deque ADT efficiently using either an array or a linked list for storing elements.
Implementing a Deque with a Circular Array
If using an array, we recommend a representation similar to the ArrayQueue class, treating the array in circular fashion and storing the index of the first element and the current size of the deque as fields; the index of the last element can be calculated, as needed, using modular arithmetic.
One extra concern is avoiding use of negative values with the modulo operator. When removing the first element, the front index is advanced in circular fashion, with the assignment f = (f+1) % N. But when an element is inserted at the front, the first index must effectively be decremented in circular fashion and it is a mistake to assign f = (f−1) % N. The problem is that when f is 0, the goal should be to “decrement” it to the other end of the array, and thus to index N−1. However, a calculation such as −1 % 10 in Java results in the value −1. A standard way to decrement an index circularly is instead to assign f = (f−1+N) % N. Adding the additional term of N before the modulus is calculated assures that the result is a positive value. We leave details of this approach to Exercise P-6.40.
Implementing a Deque with a Doubly Linked List
Because the deque requires insertion and removal at both ends, a doubly linked list is most appropriate for implementing all operations efficiently. In fact, the DoublyLinkedList class from Section 3.4.1 already implements the entire Deque interface; we simply need to add the declaration “implements Deque<E>” to that class definition in order to use it as a deque.
Performance of the Deque Operations
Table 6.5 shows the running times of methods for a deque implemented with a doubly linked list. Note that every method runs in O(1) time.
| Method | Running Time |
| size, isEmpty | O(1) |
| first, last | O(1) |
| addFirst, addLast | O(1) |
| removeFirst, removeLast | O(1) |
Table 6.5: Performance of a deque realized by either a circular array or a doubly linked list. The space usage for the array-based implementation is O(N), where N is the size of the array, while the space usage of the doubly linked list is O(n) where n < N is the actual number of elements in the deque.
6.3.3 Deques in the Java Collections Framework
The Java Collections Framework includes its own definition of a deque, as the java.util.Deque interface, as well as several implementations of the interface including one based on use of a circular array (java.util.ArrayDeque) and one based on use of a doubly linked list (java.util.LinkedList). So, if we need to use a deque and would rather not implement one from scratch, we can simply use one of those built-in classes.
As is the case with the java.util.Queue class (see page 240), the java.util.Deque provides duplicative methods that use different techniques to signal exceptional cases. A summary of those methods is given in Table 6.6.
Table 6.6: Methods of our deque ADT and the corresponding methods of the java.util.Deque interface.
When attempting to access or remove the first or last element of an empty deque, the methods in the middle column of Table 6.6—that is, getFirst(), getLast(), removeFirst(), and removeLast()—throw a NoSuchElementException. The methods in the rightmost column—that is, peekFirst(), peekLast(), pollFirst(), and pollLast()—simply return the null reference when a deque is empty. In similar manner, when attempting to add an element to an end of a deque with a capacity limit, the addFirst and addLast methods throw an exception, while the offerFirst and offerLast methods return false.
The methods that handle bad situations more gracefully (i.e., without throwing exceptions) are useful in applications, known as producer-consumer scenarios, in which it is common for one component of software to look for an element that may have been placed in a queue by another program, or in which it is common to try to insert an item into a fixed-sized buffer that might be full. However, having methods return null when empty are not appropriate for applications in which null might serve as an actual element of a queue.
6.4 Exercises
Reinforcement
| R-6.1 | Suppose an initially empty stack S has performed a total of 25 push operations, 12 top operations, and 10 pop operations, 3 of which returned null to indicate an empty stack. What is the current size of S? |
| R-6.2 | Had the stack of the previous problem been an instance of the ArrayStack class, from Code Fragment 6.2, what would be the final value of the instance variable t? |
| R-6.3 | What values are returned during the following series of stack operations, if executed upon an initially empty stack? push(5), push(3), pop(), push(2), push(8), pop(), pop(), push(9), push(1), pop(), push(7), push(6), pop(), pop(), push(4), pop(), pop(). |
| R-6.4 | Implement a method with signature transfer(S, T) that transfers all elements from stack S onto stack T, so that the element that starts at the top of S is the first to be inserted onto T, and the element at the bottom of S ends up at the top of T. |
| R-6.5 | Give a recursive method for removing all the elements from a stack. |
| R-6.6 | Give a precise and complete definition of the concept of matching for grouping symbols in an arithmetic expression. Your definition may be recursive. |
| R-6.7 | Suppose an initially empty queue Q has performed a total of 32 enqueue operations, 10 first operations, and 15 dequeue operations, 5 of which returned null to indicate an empty queue. What is the current size of Q? |
| R-6.8 | Had the queue of the previous problem been an instance of the ArrayQueue class, from Code Fragment 6.10, with capacity 30 never exceeded, what would be the final value of the instance variable f? |
| R-6.9 | What values are returned during the following sequence of queue operations, if executed on an initially empty queue? enqueue(5), enqueue(3), dequeue(), enqueue(2), enqueue(8), dequeue(), dequeue(), enqueue(9), enqueue(1), dequeue(), enqueue(7), enqueue(6), dequeue(), dequeue(), enqueue(4), dequeue(), dequeue(). |
| R-6.10 | Give a simple adapter that implements the stack ADT while using an instance of a deque for storage. |
| R-6.11 | Give a simple adapter that implements the queue ADT while using an instance of a deque for storage. |
| R-6.12 | What values are returned during the following sequence of deque ADT operations, on an initially empty deque? addFirst(3), addLast(8), addLast(9), addFirst(1), last(), isEmpty(), addFirst(2), removeLast(), addLast(7), first(), last(), addLast(4), size(), removeFirst(), removeFirst(). |
| R-6.13 | Suppose you have a deque D containing the numbers (1,2,3,4,5,6,7,8), in this order. Suppose further that you have an initially empty queue Q. Give a code fragment that uses only D and Q (and no other variables) and results in D storing the elements in the order (1,2,3,5,4,6,7,8). |
| R-6.14 | Repeat the previous problem using the deque D and an initially empty stack S. |
| R-6.15 | Augment the ArrayQueue implementation with a new rotate() method having semantics identical to the combination, enqueue(dequeue()). But, your implementation should be more efficient than making two separate calls (for example, because there is no need to modify the size). |
Creativity
| C-6.16 | Suppose Alice has picked three distinct integers and placed them into a stack S in random order. Write a short, straightline piece of pseudocode (with no loops or recursion) that uses only one comparison and only one variable x, yet that results in variable x storing the largest of Alice's three integers with probability 2/3. Argue why your method is correct. |
| C-6.17 | Show how to use the transfer method, described in Exercise R-6.4, and two temporary stacks, to replace the contents of a given stack S with those same elements, but in reversed order. |
| C-6.18 | In Code Fragment 6.8 we assume that opening tags in HTML have form <name>, as with <li>. More generally, HTML allows optional attributes to be expressed as part of an opening tag. The general form used for expressing an attribute is <name attribute1="value1" attribute2="value2">; for example, a table can be given a border and additional padding by using an opening tag of <table border="3" cellpadding="5">. Modify Code Fragment 6.8 so that it can properly match tags, even when an opening tag may include one or more such attributes. |
| C-6.19 | Postfix notation is an unambiguous way of writing an arithmetic expression without parentheses. It is defined so that if “(exp1) op (exp2)” is a normal fully parenthesized expression whose operation is op, the postfix version of this is “pexp1 pexp2 op”, where pexp1 is the postfix version of exp1 and pexp2 is the postfix version of exp2. The postfix version of a single number or variable is just that number or variable. So, for example, the postfix version of “((5+2) * (8 − 3))/4” is “5 2 + 8 3 − * 4 /”. Describe a nonrecursive way of evaluating an expression in postfix notation. |
| C-6.20 | Suppose you have three nonempty stacks R, S, and T. Describe a sequence of operations that results in S storing all elements originally in T below all of S's original elements, with both sets of those elements in their original order. The final configuration for R should be the same as its original configuration. For example, if R = (1,2,3), S = (4,5), and T = (6,7,8,9), when ordered from bottom to top, then the final configuration should have R = (1,2,3) and S = (6,7,8,9,4,5). |
| C-6.21 | Describe a nonrecursive algorithm for enumerating all permutations of the numbers {1,2,...,n} using an explicit stack. |
| C-6.22 | Alice has three array-based stacks, A, B, and C, such that A has capacity 100, B has capacity 5, and C has capacity 3. Initially, A is full, and B and C are empty. Unfortunately, the person who programmed the class for these stacks made the push and pop methods private. The only method Alice can use is a static method, dump(S,T), which transfers (by iteratively applying the private pop and push methods) elements from stack S to stack T until either S becomes empty or T becomes full. So, for example, starting from our initial configuration and performing dump(A,C) results in A now holding 97 elements and C holding 3. Describe a sequence of dump operations that starts from the initial configuration and results in B holding 4 elements at the end. |
| C-6.23 | Show how to use a stack S and a queue Q to generate all possible subsets of an n-element set T nonrecursively. |
| C-6.24 | Suppose you have a stack S containing n elements and a queue Q that is initially empty. Describe how you can use Q to scan S to see if it contains a certain element x, with the additional constraint that your algorithm must return the elements back to S in their original order. You may only use S, Q, and a constant number of other primitive variables. |
| C-6.25 | Describe how to implement the stack ADT using a single queue as an instance variable, and only constant additional local memory within the method bodies. What is the running time of the push(), pop(), and top() methods for your design? |
| C-6.26 | When implementing the ArrayQueue class, we initialized f =0 (at line 5 of Code Fragment 6.10). What would happen had we initialized that field to some other positive value? What if we had initialized it to −1? |
| C-6.27 | Implement the clone() method for the ArrayStack class. (See Section 3.6 for a discussion of cloning data structures.) |
| C-6.28 | Implement the clone() method for the ArrayQueue class. (See Section 3.6 for a discussion of cloning data structures.) |
| C-6.29 | Implement a method with signature concatenate(LinkedQueue<E> Q2) for the LinkedQueue<E> class that takes all elements of Q2 and appends them to the end of the original queue. The operation should run in O(1) time and should result in Q2 being an empty queue. |
| C-6.30 | Give a pseudocode description for an array-based implementation of the double-ended queue ADT. What is the running time for each operation? |
| C-6.31 | Describe how to implement the deque ADT using two stacks as the only instance variables. What are the running times of the methods? |
| C-6.32 | Suppose you have two nonempty stacks S and T and a deque D. Describe how to use D so that S stores all the elements of T below all of its original elements, with both sets of elements still in their original order. |
| C-6.33 | Alice has two circular queues, C and D, which can store integers. Bob gives Alice 50 odd integers and 50 even integers and insists that she stores all 100 integers in C and D. They then play a game where Bob picks C or D at random and then applies the rotate() method to the chosen queue a random number of times. If the last number to be rotated at the end of this game is odd, Bob wins. Otherwise, Alice wins. How can Alice allocate integers to queues to optimize her chances of winning? What is her chance of winning? |
| C-6.34 | Suppose Bob has four cows that he wants to take across a bridge, but only one yoke, which can hold up to two cows, side by side, tied to the yoke. The yoke is too heavy for him to carry across the bridge, but he can tie (and untie) cows to it in no time at all. Of his four cows, Mazie can cross the bridge in 2 minutes, Daisy can cross it in 4 minutes, Crazy can cross it in 10 minutes, and Lazy can cross it in 20 minutes. Of course, when two cows are tied to the yoke, they must go at the speed of the slower cow. Describe how Bob can get all his cows across the bridge in 34 minutes. |
Projects
| P-6.35 | Implement a program that can input an expression in postfix notation (see Exercise C-6.19) and output its value. |
| P-6.36 | When a share of common stock of some company is sold, the capital gain (or, sometimes, loss) is the difference between the share's selling price and the price originally paid to buy it. This rule is easy to understand for a single share, but if we sell multiple shares of stock bought over a long period of time, then we must identify the shares actually being sold. A standard accounting principle for identifying which shares of a stock were sold in such a case is to use a FIFO protocol—the shares sold are the ones that have been held the longest (indeed, this is the default method built into several personal finance software packages). For example, suppose we buy 100 shares at $20 each on day 1, 20 shares at $24 on day 2, 200 shares at $36 on day 3, and then sell 150 shares on day 4 at $30 each. Then applying the FIFO protocol means that of the 150 shares sold, 100 were bought on day 1, 20 were bought on day 2, and 30 were bought on day 3. The capital gain in this case would therefore be 100 · 10+20 · 6+30 · (−6), or $940. Write a program that takes as input a sequence of transactions of the form “buy x share(s) at $y each” or “sell x share(s) at $y each,” assuming that the transactions occur on consecutive days and the values x and y are integers. Given this input sequence, the output should be the total capital gain (or loss) for the entire sequence, using the FIFO protocol to identify shares. |
| P-6.37 | Design an ADT for a two-color, double-stack ADT that consists of two stacks—one “red” and one “blue”—and has as its operations color-coded versions of the regular stack ADT operations. For example, this ADT should support both a redPush operation and a bluePush operation. Give an efficient implementation of this ADT using a single array whose capacity is set at some value N that is assumed to always be larger than the sizes of the red and blue stacks combined. |
| P-6.38 | The introduction of Section 6.1 notes that stacks are often used to provide “undo” support in applications like a Web browser or text editor. While support for undo can be implemented with an unbounded stack, many applications provide only limited support for such an undo history, with a fixed-capacity stack. When push is invoked with the stack at full capacity, rather than throwing an exception, a more typical semantic is to accept the pushed element at the top while “leaking” the oldest element from the bottom of the stack to make room. Give an implementation of such a LeakyStack abstraction, using a circular array. |
| P-6.39 | Repeat the previous problem using a singly linked list for storage, and a maximum capacity specified as a parameter to the constructor. |
| P-6.40 | Give a complete implementation of the Deque ADT using a fixed-capacity array, so that each of the update methods runs in O(1) time. |
Chapter Notes
We were introduced to the approach of defining data structures first in terms of their ADTs and then in terms of concrete implementations by the classic books by Aho, Hopcroft, and Ullman [5, 6]. Exercises C-6.22, C-6.33, and C-6.34 are similar to interview questions said to be from a well-known software company. For further study of abstract data types, see Liskov and Guttag [67] and Demurjian [28].