3.8. Autocalibration

As shown by Theorem 5, for a completely uncalibrated image sequence, the reconstruction is only determined up to a projective transformation. While it is true that the full calibration is often not available, some knowledge of the camera intrinsics is usually available. This knowledge can be used to recover the structure and motion up to a similarity transformation. This type of approach is called autocalibration or self-calibration in the literature. A first class of algorithms assumes constant, but unknown, intrinsic camera parameters [16, 21, 44, 28, 65]. Another class of algorithms assumes some intrinsic camera parameters to be known, while others can vary [47, 29]. Specific algorithms have also been proposed for restricted camera motion, such as pure rotation [20, 11], or restricted scene structure, such as planar scenes [66].

The absolute conic and its image

The central concept for autocalibration is the absolute conic. As stated in Proposition 3, the absolute conic allows us to identify the similarity structure in a projective space. In other words, if, given a projective reconstruction, we could locate the conic corresponding to the absolute conic in the real world, this would be equivalent to recovering the structure of the observed scene up to a similarity. In this case, a transformation that transforms the absolute conic to its canonical representation in Euclidean space-that is, Ω' = diag(l, 1, 1, 0)-would yield a reconstruction similar to the original (i.e., identical up to orientation, position, and scale).

As was seen in Proposition 6, the image of the absolute conic is directly related to the intrinsic camera parameters, and this independently of the choice of projective basis:

Equation 3.38

Therefore, constraints on the intrinsics can be used to constrain the location of the conic corresponding to the absolute conic. Most autocalibration algorithms are based on (3.38).

Critical motion sequences

Autocalibration is not always guaranteed to yield a unique solution. Depending on the available constraints on the intrinsics and on the camera motion, the remaining ambiguity on the reconstruction might be larger than a similarity. This problem was identified as the problem of critical motion sequences. The first complete analysis of the problem for constant intrinsic camera parameters was made by Sturm [61]. Analysis for some other cases can be found in [62, 43, 32]. It was also shown that in some cases, the ambiguity notwithstanding, correct novel views could be generated [45].

Linear autocalibration

In this section, we present a simple linear algorithm for autocalibration of cameras. The approach, published in [49], is related to the initial approach published in [46], but avoids most of the problems due to critical motion sequences by incorporating more a priori knowledge. As input, it requires a projective representation of the camera projection matrices.

As discussed in Section 3.4.3, for most cameras it is reasonable to assume that the pixels are close to square and that the principal point is close to the center of the image. The focal length (measured in pixel units) is typically of the same order of magnitude as the image size. It is therefore a good idea to perform the following normalization:

Equation 3.39

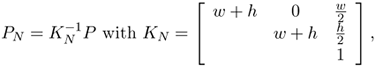
where w and h are the width and height respectively of the image. After normalization, the focal length should be of the order of unity and the principal point should be close to the origin. The above normalization would scale a focal length of a 60mm lens to 1, and thus focal lengths in the range of 20mm to 180mm would end up in the range [1/3, 3], and the principal point should now be close to the origin. The aspect ratio is typically around 1, and the skew can be assumed 0 for all practical purposes. Making this a priori knowledge more explicit and estimating reasonable standard deviations yields ƒ ≈ rƒ ≈ 1 ± 3, u ≈ v ≈ 0 ± 0.1, r ≈ 1 ± 0.1, and s = 0, which approximately translates to the following expectations for ω':

Equation 3.40

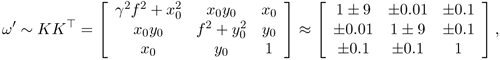
and . These constraints can also be used to constrain the left-hand side of (3.38). The uncertainty can be accounted for by weighting the equations, yielding the following set of constraints:

Equation 3.41

with P_i the i-th row of P and v a scale factor that can be set to 1. If for the solution P₃ Ω' P₃ ^T varies widely for the different views, we might want to iterate with , with the result of the previous iteration. Since Ω' is a symmetric 4 × 4 matrix, it is linearly parametrized by 10 coefficients. An estimate of the dual absolute quadric Ω' can be obtained by solving the above set of equations for all views through homogeneous linear least-squares. The rank-3 constraint can be imposed by forcing the smallest singular value to zero. The upgrading transformation T can be obtained from diag (1, 1, 1, 0) = TΩ'T^T by decomposition of Ω'.

Autocalibration refinement

This result can be further refined through bundle adjustment (see Section 3.7.2). In this case, the constraints on the intrinsics should be enforced during the minimization process. Constraints on the intrinsics can be enforced either exactly through parametrization or approximately by adding a residual for the deviation from the expected value in the global minimization process.