Recall from Chapter 4 that a proposition is a statement that’s unequivocally either true or false. Given some specified set of propositions, we can combine propositions from that set in a variety of ways to form further propositions, using the connectives NOT, AND, OR, IF...THEN...(or IMPLIES), and IF AND ONLY IF (or BI-IMPLIES, or IS EQUIVALENT TO, or simply IFF). For example, here are some of the many propositions that can be formed from the set of propositions (a) Jupiter is a star, (b) Mars has two moons, and (c) Venus is between Earth and Mercury:

Clearly, the connectives can be regarded as logical operators: they take propositions as their input and return another proposition as their output. (I’ve used parentheses in the examples to make the scope of the connectives clear. In practice, we adopt certain precedence rules that allow us to omit many of the parentheses that might otherwise be needed. Of course, it’s never wrong to include them, even when they’re logically unnecessary.)

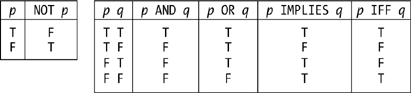
A proposition that involves no connectives at all is called a simple proposition; a proposition that isn’t simple is called compound . The truth value of a compound proposition can be determined from the truth values of the constituent simple propositions in accordance with the familiar truth tables:

For space reasons I’ve abbreviated TRUE and FALSE to just T and F, respectively. By way of example, consider the following compound proposition:

This proposition is of the form IF p THEN q (or p IMPLIES q). Both constituent simple propositions evaluate to TRUE; the truth table for IMPLIES therefore shows us that the overall proposition evaluates to TRUE also. However, a point arises here that sometimes causes confusion. In the real world, the fact that Venus is between Earth and Mercury obviously has nothing to do with whether Mars has two moons. In logic, however, we simply define IF p THEN q to be true if q is true, regardless of whether p is true; in fact, if p is false, we define IF p THEN q to be true, regardless of the truth value of q. Thus, for example, IF (Jupiter is a star) THEN (Earth has two moons) is true! You can interpret this state of affairs as saying, in effect, that if you’ll believe a falsehood (p), then you’ll believe anything (q).

It follows from the foregoing that the proposition p IMPLIES q (or IF p THEN q) is logically equivalent to the proposition (NOT p) or q—it evaluates to FALSE if and only if p evaluates to TRUE and q to FALSE. This equivalence illustrates the point that the connectives NOT, AND, OR, IMPLIES, and IFF aren’t all primitive. In fact, all possible logical connectives involving either one or two propositions can be expressed in terms of suitable combinations of NOT and either AND or OR. (Exercise: Check this claim.) Perhaps even more remarkably, all such connectives can in fact be expressed in terms of just one primitive. Can you find it?

Consider the following statements:

These statements aren’t propositions, because they aren’t unequivocally either true or false. And the reason they aren’t is that they involve parameters (also known as placeholders or free variables). For example, the statement "x is a star” involves the parameter x, and we obviously can’t say whether it’s true or false unless we’re told what that x stands for (at which point we’re no longer dealing with the given statement anyway but a different one instead—see the next paragraph).

Now, we can substitute arguments for the parameters and thereby obtain propositions from the statements. For example, if we substitute the argument The Sun for the parameter x in "x is a star,” we obtain “The Sun is a star.” And this statement is indeed a proposition because it’s unequivocally either true or false (in fact, of course, it’s true). But the original statement as such (”x is a star”) is, to say it again, not itself a proposition. Rather, it’s a predicate , which—as you’ll recall from Chapter 4—is a truth-valued function; that is, it’s a function that, when invoked, returns a truth value. Like all functions, a predicate has a set of parameters; when it’s invoked, arguments are substituted for the parameters; substituting arguments for the parameters effectively converts the predicate into a proposition; and we say the arguments satisfy the predicate if and only if that proposition is true. For example, the argument The Sun satisfies the predicate "x is a star,” whereas the argument The Moon does not.

As an aside, I remind you from Chapter 4 that logicians speak not of invoking a predicate but rather of instantiating it. In fact, for reasons that need not concern us here, their concept of instantiation is slightly more general than that of the familiar notion of function invocation. However, I’ll stay with the terminology of invocation in this appendix.

I also remind you from Chapter 4 that a proposition can be regarded as a degenerate predicate. To be precise, it’s a predicate for which the corresponding set of parameters is empty (and the function thus always returns the same result, either TRUE or FALSE, every time it’s invoked). In other words, all propositions are predicates, but most predicates aren’t propositions.

Now consider the example "x has n moons.” Obviously, this predicate involves two parameters, x and n. Substituting the arguments Mars for x and 2 for n yields a true proposition; substituting the arguments Earth for x and 2 for n yields a false one.

Predicates can conveniently be classified according to the cardinality of their set of parameters. That is, we often speak of an n-place predicate, meaning a predicate with exactly n parameters; for example, "x is between y and z" is a 3-place predicate, while "x has n moons” is a 2-place predicate. A proposition is a 0-place predicate.

Given a set of predicates, we can combine predicates from that set in a variety of ways to form further predicates, using the logical connectives already discussed—NOT, AND, OR, and so forth (in other words, those connectives are logical operators that operate on predicates in general, not just on the special predicates that happen to be propositions). A predicate that involves no connectives is called simple ; a predicate that isn’t simple is called compound . Here’s a trivial example of a compound predicate:

This predicate is also dyadic— not because it involves two simple predicates, but because it involves two parameters, x and y.

I showed in the previous section that one way to get a proposition from a predicate is to invoke it with an appropriate set of arguments. But there’s another way, too, and that’s by means of quantification. Let p(x) be a monadic predicate (I show the single parameter x explicitly, for clarity). Then:

The expression:

   EXISTS x ( p ( x ) )

is a proposition, and it means: “There exists at least one possible argument value a corresponding to the parameter x such that p(a) evaluates to TRUE” (in other words, the argument value a satisfies predicate p). For example, if p is the predicate "x is a logician,” then:

    EXISTS x ( x is a logician )

is a proposition—one that evaluates to TRUE, as it happens (for example, take a to be Bertrand Russell).

The expression:

    FORALL 
            x ( p ( x ) )

is a proposition, and it means: “All possible argument values a corresponding to the parameter x are such that p(a) evaluates to TRUE” (in other words, all such argument values a satisfy predicate p). For example, if again p is the predicate "x is a logician,” then:

    FORALL x ( x is a logician )

is a proposition—one that evaluates to FALSE, as it happens (for example, take a to be George W. Bush).

Observe that it’s sufficient to produce a single example to show the truth of the EXISTS proposition and a single counterexample to show the falsity of the FORALL proposition. Observe too in both cases that the parameter must be constrained to “range over” some set of permissible values (the set of all people, in the example). I’ll come back to this point later, in the section "Database Constraints.”

The term used in logic for the expressions EXISTS x and FORALL x in the foregoing discussion is quantifiers (the term derives from the verb to quantify, which simply means to express as a quantity— that is, to say how much of something there is or how many somethings there are). Quantifiers of the form EXISTS...are said to be existential ; quantifiers of the form FORALL...are said to be universal . (And in logic texts, EXISTS is usually represented by a backward E and FORALL by an upside-down A. I use the keywords EXISTS and FORALL for typographical reasons—not to mention readability.)

By way of another example, let q be the dyadic predicate "x is taller than y.” If we “quantify existentially over x,” we obtain:

    EXISTS x ( x is taller than y )

Now, this statement is not a proposition, because it isn’t unequivocally either true or false; in fact, it’s a monadic predicate—it has a single parameter, y. Suppose we invoke this predicate with argument Steve. We obtain:

    EXISTS x ( x is taller than Steve )

This statement is a proposition (and if there exists at least one person—Arnold, say—who’s taller than Steve, then it evaluates to TRUE, of course). But another way to obtain a proposition from the original predicate q is to quantify over both of the parameters x and y. For example:

    EXISTS x ( EXISTS y ( x is taller than y ) )

This statement is indeed a proposition; it evaluates to FALSE only if nobody is taller than anybody else and to TRUE otherwise (think about it!).

There are several lessons to be learned from this example:

I said earlier that another term for what I’ve been calling parameters is free variables. Quantifying over a free variable converts it into a bound variable . For example, consider again the 2-place predicate q from the previous section:

            x is taller than y
         

The parameters x and y here are free variables. If we now “quantify existentially” over x, we obtain:

    EXISTS x ( x is taller than y )

Here, y is still free, but x is now bound. And in the “fully quantified” form:

    EXISTS x EXISTS y ( x is taller than y )

x and y are both bound, and there are no free variables at all (the predicate has degenerated to a proposition).

Now, we already know that free variables correspond to parameters, in conventional programming terms. Bound variables, by contrast, don’t have an exact counterpart in conventional programming terms at all; instead, they serve as a kind of dummy— they serve only to link the predicate inside the parentheses to the quantifier outside. For example, consider the simple predicate (actually a proposition):

    EXISTS x ( x > 3 )

This proposition merely asserts that there exists some integer greater than three. (I’m assuming that x here is constrained to “range over” the set of integers. Again, this is a point I’ll come back to in the section "Database Constraints.”) Note, therefore, that the meaning of the proposition would remain totally unchanged if the two x’s were both replaced by some other variable y. In other words, the proposition:

    EXISTS y ( y > 3 )

is semantically identical to the one just shown.

Now consider the predicate:

    EXISTS x ( x > 3 ) AND x < 0

Here there are three x’s, but they don’t all denote the same thing. The first two are bound and can be replaced by, say, y without changing the overall meaning; but the third is free and cannot be replaced with impunity. Thus, of the following two predicates, the first is equivalent to the one just shown and the second is not:

    EXISTS y ( y > 3 ) AND x < 0
    EXISTS y ( y > 3 ) AND y < 0

To close this section, I remark that we can now (re)define a proposition to be a predicate in which all of the variables are bound.

This section discusses a number of miscellaneous issues regarding quantification.

    EXISTS x ( x is taller than Steve )

    NOT ( FORALL x ( NOT ( x is taller than Steve ) ) )

    EXISTS x ( p ( x ) )

    NOT ( FORALL x ( NOT ( p ( x ) ) )

    FORALL x ( p ( x ) )

    NOT ( EXISTS x ( NOT ( p ( x ) ) )

               s WHERE FORALL p EXISTS sp ( s.SNO = sp.SNO AND sp.PNO = p.PNO )

    SELECT s.*
    FROM   S AS s
    WHERE  NOT EXISTS
         ( SELECT p.*
           FROM   P AS p
           WHERE  NOT EXISTS
                ( SELECT sp.*
                  FROM   SP AS sp
                  WHERE  s.SNO = sp.SNO
                  AND    sp.PNO = p.PNO ) )

    EXISTS x ( p ( x ) )

NOT ( FORALL x ( NOT ( p ( x ) ) )

               s WHERE FORALL p
          ( IF p.COLOR = 'Purple'
            THEN EXISTS sp ( s.SNO = sp.SNO AND sp.PNO = p.PNO ) )

    EXISTS x ( p ( x ) )

    FALSE OR p ( x1 ) OR p ( x2 ) OR ... OR p ( xn )

    FALSE OR ( Mercury has a moon ) OR ( Venus has a moon )
          OR ( Earth has a moon )   OR ( Mars has a moon )

    FORALL x ( p ( x ) )

    TRUE AND p ( x1 ) AND p ( x2 ) AND ... AND p ( xn )

    TRUE AND ( Mercury has a moon ) AND ( Venus has a moon )
         AND ( Earth has a moon )   AND ( Mars has a moon )

    there exist at least three x's such that

    a majority of x's are such that

    an odd number of x's are such that

    UNIQUE x ( x is taller than Arnold )

    UNIQUE x ( x has social security number y )

    FORALL y UNIQUE x ( x has social security number y )

    FORALL x UNIQUE y ( x has social security number y )

Now let me show how the ideas I’ve been discussing can be used in the formulation of database constraints, using examples from Chapter 6. Please note that the formulations shown aren’t the only ones possible, in general.

Now, I’m sure you can see that many constraints are going to involve a proposition of the general form just illustrated:

    FORALL t ( IF t 
            ∊ 
            R THEN p )

(where p is some predicate). We can simplify such propositions slightly by defining the following as a shorthand:

    FORALL t 
            ∊ 
            R ( p )

The bound variable t here is said to range over (the current value of) relvar R, and the expression FORALL t ∊ R is said to be a range-coupled quantifier. Using this shorthand, constraint C1 becomes:

    CONSTRAINT C1
       FORALL s 
            ∊ S ( s.STATUS ≥ 0 AND s.STATUS ≤ 100 ) ;

In the same kind of way, it’s helpful to define the expression:

    EXISTS t 
            ∊ 
            R ( p )

to be shorthand for the following:

    EXISTS t ( ( t 
            ∊ 
            R ) AND ( p ) )

In fact, we can (and I will) simplify matters still further, by allowing the ranges for bound variables to be defined external to the expressions that use those bound variables. For example:

            s RANGES OVER { S }

Now I can reduce constraint C1 to just:^[*]

    CONSTRAINT C1
       FORALL s ( s.STATUS ≥ 0 AND s.STATUS ≤ 100 ) ;

For the remainder of this section (and the next), I’ll assume the following range definitions are in effect:

            s RANGES OVER { S }
    x RANGES OVER { S }
    y RANGES OVER { S }
    p RANGES OVER { P }
    sp RANGES OVER { SP }

I’ll also introduce additional bound variables as and when necessary.

I’ll show a few more examples (not based on examples in Chapter 6) in order to illustrate some additional points.

In this section I’ll show how the calculus notation can be used to formulate queries, using examples from Chapter 5. Again, please note that the formulations shown aren’t the only ones possible, in general.

I’ll finish up this appendix with a few remarks on certain equivalences that might have already occurred to you. First, recall the IS_EMPTY operator, which I introduced in Chapter 5 and made much use of in Chapter 6. Well, if the system supports that operator, there’s no logical need for it to support the quantifiers, thanks to the following equivalences:

    EXISTS x ( p)  ≡  NOT ( IS_EMPTY ( x WHERE p ) )

and:

    FORALL x ( p )  ≡  IS_EMPTY ( x WHERE NOT ( p) )

In fact, the SQL support for quantifiers, such as it is, is based on exactly the foregoing equivalences. To be specific, SQL supports an EXISTS operator— not really a quantifier as such, because it doesn’t involve any bound variables—that’s defined as follows: the operator invocation EXISTS(tx), where tx is a table expression, returns TRUE if and only if the table t denoted by the expression tx is nonempty.^[*] By contrast, SQL doesn’t support a FORALL operator, because (a) we don’t need both EXISTS and FORALL, and (b) more to the point, syntax of the form FORALL(tx) where tx is a table expression really makes no sense. For example, what could an expression like FORALL (SELECT * FROM S) possibly mean?

In a similar fashion, we don’t absolutely need the quantifiers anyway if the system supports the aggregate operator COUNT. This is because of the following equivalences:

    EXISTS x ( p )  ≡  COUNT ( x WHERE p ) > 0

and:

    FORALL x ( p )  ≡  COUNT ( x WHERE p ) = COUNT ( x )

Now, I’m certainly not a fan of the idea of replacing quantified expressions by expressions involving COUNT invocations—though sometimes we have to, if we’re in a pure algebraic framework—but it would be wrong of me not to mention the possibility.

In the introduction to this appendix, I said it was my position that database professionals should have at least a nodding acquaintance with the basic concepts of relational calculus (or predicate logic—it comes to the same thing). I’d like to conclude by trying to justify that position.

My basic point is simply that a knowledge of logic helps you think precisely (and in our field, the importance of thinking precisely is surely paramount). In particular, it forces you to appreciate the significance of proper quantification. Natural language is so often imprecise; however, careful consideration of what quantification is needed allows you to pin down the meaning of what can otherwise be very imprecise natural-language statements. By way of example, you might like to meditate on exactly what Abraham Lincoln meant—or might have meant, or thought he might have meant, or might have thought he meant—when he famously said: “You can fool some of the people all of the time, and all of the people some of the time, but you can not fool all of the people all of the time.”

Of course, I’m well aware there are many people who disagree with me here; that is, there are many people who feel ordinary mortals shouldn’t have to grapple with a subject as abstruse as logic seems to be. In effect, they claim that logic is just too difficult for most people to deal with. Now, that claim might be true in general (logic is a big subject), but you don’t need to understand the whole of logic for the purpose at hand; in fact, I doubt whether you need much more than what I’ve covered in this appendix. And the benefits are so huge! I made essentially the same point in a 2004 article—“The Logic of Business Rules,” www.dbdebunk.com (June 2004), on which much of the present appendix is based—and I’d like to quote the concluding remarks from that article here:

As you can see, these remarks are set in the context of business rules specifically, but I think they’re of wider applicability.