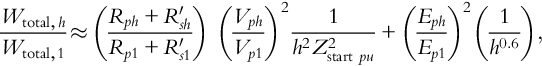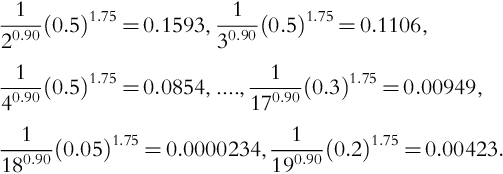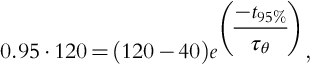Lifetime Reduction of Transformers and Induction Machines
Abstract
Investigates aging and lifetime reduction of transformers and induction machines due to elevated temperatures caused by harmonics. The additional temperature rise caused by harmonics is defined by a weighted-harmonic factor function which has not yet been published in a textbook. The Arrhenius reaction rate equation is relied on to estimate the reduction in lifetime of motors and transformers due to harmonic voltage magnitudes. Harmonic limits within single- and three-phase power systems are proposed and rigid harmonic spectra are not recommended. The probabilistic and time-varying nature of harmonics and their incurred cost are reviewed. Various operating regimes of electric machines are investigated from a lifetime reduction point of view. Heat flow relations due to radiation and convection are given with their associated thermal equivalent circuits. 11 application examples with solutions and 11 application-oriented problems are included.
The total installed power capacity within the Eastern, Western, and Texan power pools of the United States is 900 GW with about 70 GW of spinning reserve. Approximately 60% of the 900 GW is consumed by induction motors and 100% passes through transformers. Similar percentages exist in most countries around the world. For this reason transformers and induction motors are important components of the electric power system.
The lifetime of any device is limited by the aging of the insulation material due to temperature: the higher the activation energy of any material, the faster the aging proceeds. Iron and copper/aluminum have low activation energies and for this reason their aging is negligible. Insulation material – either of the organic or inorganic type – is most susceptible to aging caused by temperature. If a device is properly designed then the rated temperature results in the rated lifetime. Temperature rises above rated temperature result in a decrease of lifetime below its rated value. There are a few mechanisms by which the rated lifetime can be reduced:
1. Temperature rises above the rated temperature can come about due to overload and voltage or current harmonics.
2. Lifetime can be also decreased by intermittent operation. It is well known that generators of pumped storage plants must be rewound every 15 years as compared to 40 years for generators which operate at a constant temperature.
3. Vibration within a machine due to load variations (e.g., piston compressor) can destroy the mechanical properties of conductor insulation.
4. Faults – such as short-circuits – can impact the lifetime due to excessive mechanical forces acting on the winding and their insulation.
In this chapter we are concerned with aging due to elevated temperatures caused by harmonics. The presence of current and voltage harmonics in today’s power systems causes additional losses in electromagnetic components and appliances, creating substantial elevated temperature rises and decreasing lifetime of machines and transformers. Therefore, estimating additional losses, temperature rises, and aging of power system components and loads has become an important issue for utilities and end users alike.
Three different phases are involved in the estimation (or determination) of the lifetime of magnetic devices:
1. modeling and computation of the additional losses due to voltage or current harmonics,
2. determination of the ensuing temperature rises, and
3. estimation of the percentage decrease of lifetime as compared with rated lifetime [1].
The literature is rich in documents and papers that report the effect of poor power quality on losses and temperature rises of power system components and loads; however, a matter that still remains to be examined in more detail is the issue of device aging under nonsinusoidal operating conditions. Earlier papers were mostly concerned about magnetic device losses under sinusoidal operating conditions [2–13]. However, more recent research has expanded the scope to magnetic device derating under nonsinusoidal operation [14–17]. Only a few papers have addressed the subjects of device aging and economics issues caused by poor power quality [18–23].
In the first sections of this chapter the decrease of lifetime of power system components and loads such as universal motors, single- and three-phase transformers, and induction motors are estimated based on their terminal voltage harmonics. After a brief review of temperature relations, the concept of weighted harmonic factors is introduced. This is a quantity that relates the device terminal voltage harmonic amplitudes to its temperature rise. Additional temperature rises and losses due to harmonics are discussed, and thereafter the weighted harmonic factors are employed to determine the decrease of lifetime of electrical appliances. Toward the end of this chapter the time-varying nature of harmonics is addressed with respect to their measurement, summation, and propagation. The probabilistic evaluation of the economical damage – that is, cost – due to harmonic losses in industrial energy systems is explored next, and the increase of temperature in a device as a function of time as well as intermittent operation of devices conclude this chapter.
6.1 Rationale for relying on the worst-case conditions
Field measurements show that the harmonic voltages and currents of a distribution feeder are time-varying. This is due to:
1. the changes in the loads, and
2. the varying system’s configuration.
This means that steady-state harmonic spectra do not exist. However, loads such as variable-speed drives for air-conditioning, rolling mills, and arc furnaces operate during their daily operating cycle for at least a few hours at rated operation. It is for this operating condition that system components (e.g., transformers, capacitors) and loads must be designed. Most electromagnetic devices such as transformers and rotating machines have thermal time constants of 1 to 3 hours – depending on their sizes and cooling mechanisms. When these components continually operate at rated power, they are exposed to steady-state current and voltage spectra resulting at an ambient temperature of Tamb = 40 °C in the maximum temperature rise Trisemax, and the resulting temperature Tmax = Tamb + Trisemax must be less or equal to the rated temperature Trat. The worst case is therefore when the power system components operate at rated load with their associated current or voltage spectra where individual harmonic amplitudes are maximum. It is not sufficient to limit the total harmonic distortion of either voltage (THDv) or current (THDi) because these parameters can be the same for different spectra – resulting in different additional temperature rises, insulation stresses, and mechanical vibrations. In Sections 6.2 to 6.10 worst-case conditions will be assumed.
6.2 Elevated temperature rise due to voltage harmonics
Most electric appliances use electric motors and/or transformers. In all these cases the power system’s sinusoidal voltage causes ohmic and iron-core losses resulting in a temperature rise, which approaches the rated temperature rise (Triserat) at continuous operation:
Trat=Tamb+Triserat,
where Tamb = 40 °C is the ambient temperature. The lifetime of a magnetic device is greatly dependent on this temperature rise and the lifetime will be reduced if this rated temperature rise is exceeded over any length of time [1].
The presence of voltage harmonics in the power system’s voltage causes harmonic currents in induction motors and transformers of electrical appliances, resulting in an elevated temperature rise (Triserat + ΔTh) such that the device temperature is
T=Tamb+Triserat+▵Th,
where ΔTh is the additional temperature rise due to voltage (integer, sub-, inter-) harmonics. Through a series of studies this additional temperature rise of various electric machines and transformers was calculated and measured as a function of the harmonic amplitude Vh and the phase shifts of the voltage harmonics φh with respect to the fundamental [18,19].
The insulating material of electrical apparatus, as used in electrical appliances, is of either organic or inorganic origin. The deterioration of the insulation caused by the elevated temperature rise is manifested by a reduction of the mechanical strength and/or a change of the dielectric behavior of the insulation material. This thermal degradation is best represented by the reaction rate equation of Arrhenius. Plots which will be drawn based on this equation are called Arrhenius plots [24,25]. The slopes of these plots are proportional to the activation energy E of the insulation material under consideration. Knowing the rated lifetime of insulation materials at rated temperature (Trat =Tamb + Triserat), and the elevated temperature rise (ΔTh) due to given amplitudes Vh and phase shifts φh of voltage harmonics, one will be able to estimate from the Arrhenius plot the reduction of the lifetime of an electrical appliance due to ΔTh.
Definition: The activation energy E is the energy transmitted in the form of heat to the chemical reaction of decomposition.
6.3 Weighted-harmonic factors
The harmonic voltage content (order h, amplitude Vh, and phase shift φh) of power system voltages varies with the type and size of harmonic generators and loads as well as with the topology of the system, and it will hardly be the same for any two networks. Since voltage harmonics result in additional losses and temperature rises (ΔTh) in electrical appliances, it would be desirable to derive one single criterion which limits – for a maximum allowable additional temperature rise – the individual amplitudes and phase shifts of the occurring harmonic voltages including their relative weight with respect to each other in contributing to the elevated temperature rise ΔTh.
Also, this criterion should be simple enough so that the additional losses, temperature rises ΔTh, and the reduction of lifetime of electrical appliances can easily be predicted as a function of the harmonic content of their terminal voltages. As most electrical appliances use transformers and motors as input devices, in this section weighted harmonic factors will be derived for single-phase and three-phase transformers and induction machines.
The ambient temperature is at the most Tamb = 40 °C. The rated temperature rise depends on the class of insulation material used. Triserat = 80 °C is a commonly permitted value so that
Trat=Tamb+Triserat=40°C+80°C=120°C.
In transformers, iron-core sheets and copper (aluminum) conductors are insulated by paper, plastic material, or varnish.
The Swedish scientist Svante Arrhenius originated the so-called Arrhenius rule: a differential equation describing the speed of degradation or deterioration of any (organic, inorganic) material. This deterioration is not oxidation due to elevated temperatures.
The idea of a weighted harmonic factor for different magnetic devices [20] is based on the fact that the additional temperature rise ΔTh is different for transformers, universal machines, and induction machines, although the harmonic content (Vh, φh) of the terminal voltages is the same.
6.3.1 Weighted-Harmonic Factor for Single-Phase Transformers
Figure 6.1 illustrates the equivalent circuit of a single-phase transformer for the fundamental (h = 1) and harmonic voltages of hth order.

The ohmic losses of the hth harmonic expressed in terms of the fundamental ohmic losses are
Wohmic,hWohmic,1=(VphVp1)2(Rph+R′shRp1+R′s1)(RATIO),
where
RATIO=(Rp1+R′s1+R′load,1)2+ω2(Lp1+L′s1+L′load,1)2(Rph+R′sh+R′load,h)2+(hω)2(Lph+L′sh+L′load,h)2.
In most residential power transformers the influence of the skin effect can be neglected. However, the skin effect of an ohmic load cannot be ignored, because R′load,h,R′load,l≫Rph,Rp1,R′sh,R′s1.![]() Therefore, one obtains
Therefore, one obtains
Wohmic,hWohmic,1≈(VphVp1)2(R′load,1)2+ω2(Lp1+L′s1+L′load,1)2(R′load,h)2+(hω)2(Lph+L′sh+L′load,h)2.
Due to Lph≈Lp1,L′sh≈L′s1,L′load,h≈L′load,1,![]() and the fact that the load resistance Rload, h′ increases less than linearly with frequency [18], the following simplified expression is considered:
and the fact that the load resistance Rload, h′ increases less than linearly with frequency [18], the following simplified expression is considered:
Wohmic,hWohmic,1≈1hn(VphVp1)2,
where 0 < n < 2 depends on the resistance and inductance values of the equivalent circuit of a load.
The iron-core losses of a single-phase transformer due to a voltage harmonic of order h are expressed in terms of the corresponding losses caused by the fundamental as
Wiron,hWiron,1=(Bmax,hBmax,1)2{σ(fh100)2k2m+ɛ(fh100)}{σ(f100)2+ɛ(f100)},
where Bmax,1 and Bmax,h define fundamental and harmonic maximum flux densities, respectively, and σ and ɛ are [26] coefficients related to eddy-current and hysteresis losses, respectively. The term km takes the reaction of the eddy currents within the laminations and between the laminations on the original field into account [18]. With (h Bmax,h) ∝ Eph and Bmax,1 ∝ Ep1, the relation becomes
Wiron,hWiron,1=(EphhEp1)2(Rfe,1Rfe,h),
where Rfe,1 and Rfe,h are the iron-core loss resistances for the fundamental (h = 1) and harmonic of order h, respectively.
The total losses for a harmonic of order h are then determined from the sum of Eqs. 6-6 and 6-8:
Wtotal,hWtotal,1≈1hn(VphVp1)2+1h2(EphEp1)2(Rfe,1Rfe,h).
According to [27], the core-loss resistance ratio is Rfe,h/Rfe,1 = h0.6 and because of the leakage reactance being proportional to h, one obtains the inequality (Eph/Ep1) < Vph/Vp1) or
(EphEp1)2=(VphVp1)m,
where the exponent m is less than 2. Therefore, for single-phase transformers Eq. 6-9 becomes
Wtotal,hWtotal,1≈1hn(VphVp1)2+1h2.6(VphVp1)m.
Depending on the relative sizes of the ohmic and iron-core losses at full load, Eq. 6-11 can be rewritten for all occurring harmonics and is called the weighted harmonic factor [20]:
Wtotal,hΣWtotal,1=K1∞∑h=21(h)k(VphVp1)ℓ,
where Wtotal,hΣ and Wtotal,1 are the total harmonic losses and the total fundamental losses, respectively. Also 0 ≤ k ≤ 2.0 and 0 ≤ ℓ ≤ 2.0. Average values for k and ℓ are obtained from measurements as discussed in a later section.
6.3.2 Measured Temperature Increases of Transformers
Measured temperature rises in transformers and induction machines as they occur in a residential/commercial power system – together with calculated loss increases due to voltage harmonics – represent a base for the estimation of the lifetime reduction due to voltage harmonics. It is thereby assumed that for small additional temperature rises – as compared with the rated temperature rise – the additional losses are proportional to the additional temperature rise.
6.3.2.1 Single-Phase Transformers
A single-phase 150 VA transformer was tested [18,19] and Fig. 6.2a,b shows the measured temperature rises in percent of the rated temperature rises at full load for moderate (e.g., Tamb = 23 °C) and high (e.g., Tamb = 40 °C) ambient temperatures.

Note that if the third harmonic voltage v3(t) superposed with the fundamental voltage v1(t) produces a peak-to-peak voltage {v1(t) + v3(t)} that is maximum, then the peak-to-peak flux density in the core {B1(t) + B3(t)} is minimum. That is, the total harmonic losses are smaller than those when the peak-to-peak voltage is minimum, resulting in a maximum peak-to-peak value of the flux density. This “alternating” behavior of the harmonic losses and associated temperatures is discussed in detail in [27,28].
6.3.2.2 Three-Phase Transformers
Three 150 VA single-phase transformers were assembled to Δ/Y-grounded and Y-grounded/Y-grounded configurations and they were subjected to the same harmonic voltage conditions as the single-phase transformer of the preceding section. The temperatures of the transformer windings were measured at the same location as for the single-phase transformer. The tests were limited to balanced operation. However, no phase-lock loop was available and no stable relation between fundamental and harmonic voltage systems could be maintained. Therefore, the temperature data of Fig. 6.3a,b represent average values and the alternating behavior could not be observed, although it also exists in three-phase transformers.

6.3.3 Weighted-Harmonic Factor for Three-Phase Induction Machines
The per-phase equivalent circuits of a three-phase induction motor are shown for the fundamental (h = 1) and a (integer, sub-, inter-) harmonic of hth order in Fig. 6.4. In Fig. 6.4 the fundamental slip is
s1=ns1−nmns1,
and the harmonic slip is
sh=nsh−nmnsh.

The ohmic losses caused by either the fundamental or a harmonic of order h are proportional to the square of the respective currents. Therefore, one can write for the ohmic losses caused by voltage harmonics:
Wohmic,hWohmic,1=(Rph+R′sh(Rp1+R′s1))(VphVp1)2(Zp1Zph)2,
where
Zp1=√(Rp1+R′s1/s1)2+(ω1Lp1+ω1L′s1)2
and
Zph=√(Rph+R′sh/sh)2+(hω1Lph+hω1L′sh)2.
For all time harmonics (h = 2, 3, 4, …) an induction machine operating at rated speed can be considered being at standstill because s1< <sh. With Rph, Rʹsh/sh < < hω1Lph ≈ hω1Lp1, hω1Lʹsh ≈ hω1Lʹs1, the per-unit starting impedance
Zstartpu=√(ω1Lp1+ω1L′s1)2√(Rp1+R′s1/s1)2+(ω1Lp1+ω1L′s1)2,
and the slip sh={h∓(1–s1)}/h≈(h∓1)/h,![]() Eq. 6-14 can be rewritten as
Eq. 6-14 can be rewritten as
Wohmic,hWohmic,1=(Rph+R′sh(Rp1+R′s1))(VphVp1)21h2Z2startpu
The additional iron-core losses due to a voltage harmonic of order h referred to the iron-core losses at the fundamental frequency are (see Fig. 6.4)
Wiron,hWiron,1=(VphVp1)2(Zfe,1Zfe,h)2Rfe,hRfe,1=(EphEp1)2Rfe,1Rfe,h,
where
Zfe,1=(jω1Lm1+Rfe,1)(Rp1+jω1Lp1)jω1Lm1+Rfe,1,
Zfe,h=(jhω1Lmh+Rfe,h)(Rph+jhω1Lph)jhω1Lmh+Rfe,h,
where Lmh ≈ Lm1, Lph ≈ Lp1. From [31] follows Rfe,hRfe,1≈h0.6,![]() and therefore the iron-core losses are
and therefore the iron-core losses are
Wiron,hWiron,1≈(EphEp1)2(1h0.6).
Summing Eqs. 6-16 and 6-18, the total losses for a harmonic of order h of a three-phase induction machine become
Wtotal,hWtotal,1≈(Rph+R′shRp1+R′s1)(VphVp1)21h2Z2startpu+(EphEp1)2(1h0.6),
or for all occurring harmonics, one can show that the total harmonic losses Wtotal,hΣ relate to the total fundamental losses, as defined by the weighted harmonic factor [32]:
Wtotal,hΣWtotal,1=K2∞∑h=21(h)k(VphVp1)ℓ,
where 0 ≤ k ≤ 2 and 0 ≤ ℓ ≤ 2.
Note that the relations for single-phase transformers (Eq. 6-12) and that for a three-phase induction motor (Eq. 6-20) are identical in structure, though the exponents k and ℓ may assume different values for single-phase transformers and three-phase induction motors. These exponents will be identified in the next section and it will be shown that the same structure of the weighted harmonic factor will also be valid for three-phase transformers and single-phase induction machines as well as universal machines.
Depending on the values of k and ℓ one obtains different loss or temperature dependencies as a function of the frequency. Unfortunately, these dependencies can vary within wide ranges from constant to hyperbolic functions. This is so because the iron-core losses depend on the electric steel (e.g., conductivity, lamination thickness, permeability) used and the winding configurations in primary or stator and secondary or rotor. These can exhibit different conductivities (e.g., Cu, Al) or skin and proximity effects. In order to study these dependencies various k and ℓ combinations will be assumed, as is depicted in Figs. 6.5 to 6.7:



• k = 0 and ℓ = 1 results in a linear frequency-independent characteristic (Fig. 6.5).
• k = 1 and ℓ = 1 results in an inverse frequency-dependent characteristic (Fig. 6.6).
• k = 2 and ℓ = 2 results in a quadratic inverse frequency-dependent characteristic (Fig. 6.7).
In real transformers and induction machines combinations of these characteristics will be possible.
6.3.4 Calculated Harmonic Losses and Measured Temperature Increases of Induction Machines
6.3.4.1 Single-Phase Induction Motors
Calculated additional losses due to voltage harmonics for the machine of Eq. 6-21 are shown for the stator in Fig. 6.8a and for the rotor in Fig. 6.8b. Measured additional temperature rises of the stator end winding and that of the squirrel-cage rotor winding at full load as a function of the harmonic voltage amplitude, phase shift, and frequency for the same single-phase induction motor are depicted in Fig. 6.9a and 6.9b, respectively. Note that the maximum additional temperature rises are obtained when the peak-to-peak value of the terminal voltage is a maximum as a function of the superposed harmonic voltage with the fundamental voltage.
P=2hp,Vt=115/208V,It=24/12A,f=60Hz,η=0.73,nrat=1725rpm.


Figure 6.8a,b shows that the additional harmonic losses due to subharmonic voltages and interharmonics below the fundamental become very large, even at low percentages and, therefore, the subharmonic voltages must be limited to less than 0.5% of the fundamental. Note that at the slip frequency which corresponds to a slip of s = 0 the total stator losses reach a minimum (see Fig. 6.8a) because the total rotor losses are about zero (see Fig. 6.8b).
6.3.4.2 Three-Phase Induction Motors
Figure 6.4a,b illustrates the equivalent circuit of three-phase induction machines for the fundamental and time harmonics of order h (integer, sub-, and interharmonics). The total harmonic losses were calculated [18,19] for a three-phase induction machine with the following nameplate data and equivalent circuit parameters:
P=800W,p=4poles,nrat=1738rpm,f=60Hz,VL−L=220/380V,▵/Yconnected,Iph=2.35A,Rs1=7.0Ω,Xs1=8.0Ω,Xm1=110.0Ω,R′r1=4.65Ω,X′r1=7.3Ω.
Figure 6.10a shows the total harmonic stator losses referred to the total rated stator losses and Fig. 6.10b depicts the total harmonic rotor losses referred to the total rated rotor losses. In Fig. 6.10a there is a local maximum around 360 Hz; this maximum stems from the iron-core losses and its location depends on the lamination thickness of the iron-core sheets. The losses rapidly increase for subharmonics and interharmonics with decreasing frequency. The total harmonic rotor losses of Fig. 6.10b are larger for backward-rotating harmonic voltage systems (full lines) and smaller for forward-rotating harmonic systems (dashed lines). As for the stator, the rotor losses due to subharmonics and interharmonics below 60 Hz increase greatly with decreasing frequency. Note that at the slip frequency which corresponds to a slip of s = 0 the total stator losses reach a minimum (see Fig. 6.10a) because the total rotor losses are about zero (see Fig. 6.10b).

For the three-phase induction motor with the following nameplate data:
P=2hp,q1=3;No=LPF,f=60Hz,nrat=1725rpm,VL−L=200V,Iph=7.1A,time:continuous.
the additional temperature rise of the stator end winding for forward- and backward-rotating harmonic voltage systems superimposed with a forward voltage system of fundamental frequency of 60 Hz is shown in Fig. 6.11a. Note that for subharmonic and interharmonics below 60 Hz the stator temperature increases rapidly. The corresponding temperature rises of the squirrel-cage winding of the rotor are depicted in Fig. 6.11b and 6.11c for forward- and backward-rotating harmonic voltage systems, respectively. The temperature rise due to the backward-rotating harmonic voltage system is slightly larger than that of the forward-rotating system, if the rotor temperature rise is considered. Again, the temperature rises due to sub- and interharmonics below 60 Hz are rapidly increasing with decreasing frequency.



Figures 6.10 and 6.11 illustrate that the additional temperature rises due to subharmonic and interharmonics below 60 Hz voltages become very large, even at low percentages; therefore, the subharmonic and interharmonics below 60 Hz voltage components must be limited to less than 0.5% of the fundamental voltage. The sensitivity of large three-phase induction machines with respect to additional temperature rises has also been calculated in [34], and it is recommended to limit the subharmonic voltages to 0.1%.
6.4 Exponents of weighted-harmonic factors
In references [18,19], the functional dependencies of the additional losses and the additional temperature rises due to harmonics of the terminal voltage are calculated for linear circuits and measured for actual machines, respectively. Thereby it is assumed that the additional temperature rise is proportional to the additional losses. Inspecting these loss and temperature functions, one notes that they can be approximated by hyperbolas for h ≥ 1.0, as shown in Fig. 6.12.

For h < 1 corresponding to the slip frequency where the stator field is in synchronism with the mechanical rotor no voltage Ẽ will be induced in the rotor and the rotor currents are zero; that is, the rotor loss is zero and the total motor loss is at a minimum, as is indicated in Fig. 6.12. At very low inter- or subharmonic frequencies, say, 3 Hz, the magnetizing reactance is very small and the 3 Hz current becomes very large, resulting in large total losses and harmonic torques as discussed in Chapter 3.
Determination of Factor k
Knowing
▵Th=K1∞∑h=21(h)k(VphVp1)ℓ,
one can determine the exponent k from two given (measured) points (h1, ΔTh1) and (h2, ΔTh2) of Fig. 6.12. Therefore, one can write
k=log{▵Th2▵Th1((Vph1/Vp1)ℓ(Vph2/Vp1)ℓ)}log(h1h2).
From evaluation of measured points one finds the following [33]:
| 0.6 ≤ k ≤ 1.2 | ||
| 0.5 ≤ k ≤ 1.2 | ||
| 0.7 ≤ k ≤ 1.2 | ||
| 0.8 ≤ k ≤ 1.2 |

The average values of k = kavg for each category are also shown.
Determination of Factor ℓ
For the determination of the exponent ℓ of the weighted-harmonic factors, the functional dependencies of the additional losses and measured temperature rises on the harmonic frequencies and amplitude of references [18,19] can be used. These calculated and measured functions can be approximated by a family of hyperbolas, as shown in Fig. 6.13.

One can determine the values of the exponent ℓ from any given two points (Vph1, ΔTh1) and (Vph2, ΔTh2) of Fig. 6.13 for any given two harmonic frequencies of order h1 and h2:
ℓ=log{▵Th2▵Th1(h1h2)k}log(Vph1Vph2).
From evaluation of measured points one finds the following [33]:
| 1.50 ≤ ℓ ≤ 2.0 | ||
| 1.0 ≤ ℓ ≤ 1.80 | ||
| 1.2 ≤ ℓ ≤ 2.0 | ||
| 1.5 ≤ ℓ ≤ 2.5 |

The average values ℓ = ℓavg for each category are also shown.
6.5 Additional losses or temperature rises versus weighted-harmonic factors
The additional losses and temperature rises due to harmonics of the terminal voltage of transformers, induction machines, and universal machines are calculated and measured in references [18,19]. Provided these additional losses due to such time harmonics are small as compared with the rated losses (Wtotal,hΣ < < Wtotal,1), a proportionality between the additional losses and the additional temperature rises can be assumed because the cooling conditions are not significantly altered. Calculations and measurements show that the previously mentioned electromagnetic devices are sensitive to voltage harmonics in the frequency range 0 ≤ fh ≤ 1500 Hz. Harmonics of low order generate the largest additional loss. The correspondence of a given value of the weighted-harmonic factor (to an additional loss and temperature rise) leads to the additional temperature rise (or loss) versus the harmonic-factor function [20] as shown in Fig. 6.14.

With assumed values for the average exponents kavg and ℓavg as they apply to transformers, induction and universal machines, one can compute for given percentages of the harmonic voltages the weighted-harmonic factor and associate with it the additional losses or temperature rises.
6.5.1 Application Example 6.1: Temperature Rise of a Single-Phase Transformer due to Single Harmonic Voltage
Determine the temperature rise ΔTh of a single-phase transformer provided V3 = 0.10 pu = 10%, Tamb = 40 °C, and Trated = 100 °C. Assume kavg = 0.90 and ℓavg = 1.75.
Solution to Application Example 6.1
The rated temperature rise is ΔTrated = Trated – Tamb = Trise rat = 60 °C. For the harmonic with order h = 3 and amplitude V3 = 0.10 pu ≡ 10%, one obtains (through linear extrapolation) the weighted-harmonic factor by replacing Vph/Vp1![]() by 10:
by 10:
∑h=31(3)0.9(10)1.75=20.98,
resulting with Fig. 6.14 in the additional temperature increase due to the 3rd harmonic (average) ΔTh = 3 = 3.3% or ΔTh = 3 = 1.98 °C.
6.5.2 Application Example 6.2: Temperature Rise of a Single-Phase Induction Motor due to Single Harmonic Voltage
Determine the temperature rise ΔTh of a single-phase induction motor provided V3 = 0.10 pu ≡ 10%, Tamb = 40 °C, and Trated = 100 °C. Assume kavg = 0.85 and ℓavg = 1.40.
Solution to Application Example 6.2
The rated temperature rise is ΔTrated = Trated – Tamb = Trise rat = 60 °C. For the harmonic with order h = 3 and amplitude V3 = 0.10 pu ≡ 10% one obtains the weighted-harmonic factor by replacing Vph/Vp1![]() by 10 as follows ∑h=31(3)0.85(10)1.40=9.88,
by 10 as follows ∑h=31(3)0.85(10)1.40=9.88,![]() resulting with Fig. 6.14 in the additional temperature increase due to the 3rd harmonic (average) ΔTh = 3 = 11% or ΔTh = 3 = 6.6 °C.
resulting with Fig. 6.14 in the additional temperature increase due to the 3rd harmonic (average) ΔTh = 3 = 11% or ΔTh = 3 = 6.6 °C.
Transformers, induction machines, and universal machines have different loss or temperature sensitivities with respect to voltage harmonics and, therefore, the additional temperature rises are different for all five types of devices. The additional temperature rise (loss) versus weighted-harmonic factor function indicates that the most sensitive components are single-phase induction machines, whereas the least sensitive devices are transformers with resistive load and universal machines. This is so because for any harmonic terminal voltage, a single-phase machine (and to some degree an unbalanced three-phase induction machine) develops forward-and backward-rotating harmonic fields and responds like being under short-circuit conditions due to the large slip sh of the harmonic field with respect to the rotating rotor. In transformers the resistive and inductive loads can never have zero impedance due to the nature of the frequency dependency of such loads.
6.6 Arrhenius plots
A series of studies have investigated the behavior of various electric machines and transformers as they occur in a residential distribution system and are exposed to harmonics of the terminal voltage [18,19]. The influence of such harmonics expresses itself, among others (e.g., mechanical vibration), in an elevated (additional) temperature rise of the machine windings and iron cores. The question arises how the lifetime of the machines will be affected by such additional temperature rises.
Thermal Aging
The insulating material of an electric apparatus as used in electrical appliances is of organic or inorganic origin. Due to the heating of these materials, caused by the loss within the machine, a deterioration of the insulating materials will occur. This deterioration is manifested either by:
• lowering of the mechanical strength, and/or
• changing of the dielectric behavior of the insulating material.
It may be mentioned that not only the heat itself, but also small motions due to expansion and contraction of the wire and iron laminations, are causing deteriorations by mechanical friction. In addition, time harmonics induce small core vibrations that may aggravate the mechanical stresses. The mechanical failure of the insulation is a result of the decrease of the tensile strength or flexibility of the insulation material. The thermal lifetime of electric machines and transformers is highly dependent on the mode of utilization; there is no doubt that machines with frequently variable load are more prone to aging from a mechanical failure point of view.
All further investigations consider machines or transformers operating at constant rated load, where the chemical changes of the insulating materials are responsible only for thermal aging.
6.7 Reaction rate equation
For many years it has been recognized that thermal degradation of organic or inorganic materials can be best represented by the reaction rate equation [24, 25]
dRdt=Ae(−E/KT).
In this equation, dR/dt is the reduction in property R with respect to time, A is a constant of integration, K is the gas constant or, depending on the units, the Boltzmann constant, T is the absolute temperature in kelvin, and E is the activation energy of the aging reaction (large E leads to fast aging, small E leads to slow aging).
Equation 6-27 expresses the rule of chemical reactions which was derived by Svante Arrhenius in 1880. The form of the original Arrhenius formula can be obtained from the differential equation by integration as follows:
dR=Ae−(E/KT)dt,∫dR=A∫e−(E/KT)dt,Rt=Ae−(E/KT),ℓn(R/t)=ℓn(Ae−(E/KT)),ℓn(R)−ℓn(t)=ℓn(A)−E/KT,
or
ℓn(t)=(EK)1T+B.
The plot ℓn(t) versus 1/T is a straight line with the slope E/K, if for the lifetime t a logarithmic scale is employed, as shown in Fig. 6.15.

Equation 6-28 expresses that the logarithm of the degradation (decreased life) time t is proportional to the activation energy E: this energy is transmitted in the form of heat to the chemical reaction or decomposition. Different kinds of materials need a different amount of heat energy to arrive at the same degree of deterioration. To obtain these data in the case of insulating materials, extensive experimental research has been done [24]. In this reference, one can find not only a list of the activation energies, but the frequency distribution of the activation energies of various materials. Properties monitored for these materials include flexural strength, impact strength, and dielectric strength. In Fig. 4 of [24], one notes the number of materials for each increment of 0.1 eV activation energy (see Fig. 6.16). The peak of this distribution curve occurs at about E = 1.15 eV.

The practical use of the Arrhenius plot and the consequences of the data of Fig. 4 of [24] will be discussed in the next section.
6.8 Decrease of lifetime due to an additional temperature rise
The slope of the Arrhenius plot based on
ℓnt=(EK)1T+B
is the most important quantity (proportional to the activation energy E) for our investigation; this is the only quantity that determines the aging of the insulation material. Therefore, we have to use the slope of the Arrhenius plot as a measure of aging.
If one knows from experiments two (different) points of the plot belonging to temperatures T1 and T2 and lifetimes t1 and t2, respectively, that is, (T1, t1) and (T2, t2), then one can obtain for a given insulation material
ℓnt1−ℓnt2=(EK)(1T1−1T2).
It must be noted that if the activation energy E is measured in electron volts one has to use for K the Boltzmann constant: K = 1.38 · 10−23 J/kelvin; in case the activation energy is given in kilocalories per mole the constant K will be the gas constant K = R = 19.84 · 10−4 kcal/mol. Note that 1 eV = 1.602 · 10−19 J or 1 J = 0.624 · 1019 eV.
Suppose one knows the rated lifetime t2 of an apparatus and its rated (constant) temperature T2 at which it is operating. The question arises to what extent the lifetime decreases provided the elevated temperature becomes T1 = T2 + ΔT where ΔT = ΔTh. To answer this question one has to substitute in Eq. 6-30 T1 by T2 + ΔT:
ℓnt1−ℓnt2=(EK)(1T2+▵T−1T2).
After some manipulations, the new decreased lifetime is
t1=t2e−(EK)▵TT2(T2+▵T),
where t2 is the rated lifetime, T2 is the rated temperature in kelvin, and ΔT is the (additional) temperature rise in degrees Celsius. Several examples will illustrate the use of the above relation as applied to the calculation of the decrease of the lifetime due to the additional temperature rise caused by the additional harmonic losses. In all following examples it is assumed that the rated lifetime of the apparatus is t2 = 40 years, and the steady-state rated temperature of the hottest spot is T2 = 100 °C ≡ 273 + 100 = 373 kelvin.
6.8.1 Application Example 6.3: Aging of a Single-Phase Induction Motor with E = 0.74 eV Due to a Single Harmonic Voltage
Determine for an activation energy of E = 0.74 eV the slope E/K and for the additional temperature rise ΔTh = 3 = 6.6 °C (see Application Example 6.2 with Tamb = 40°, T2 = Trat = 100 °C) the reduced lifetime of a single-phase induction motor.
Solution to Application Example 6.3
The slope (E/K) is E/K = 8.58·103 kelvin. Thus one obtains from t1=40e−8.58⋅103▵Th/373(373+▵Th)![]() , with ΔTh = 3 = 6.6 °C, a reduced lifetime of t1|▵Th=3=6.6°C=26.81years
, with ΔTh = 3 = 6.6 °C, a reduced lifetime of t1|▵Th=3=6.6°C=26.81years![]() .
.
6.8.2 Application Example 6.4: Aging of a Single-Phase Induction Motor with E = 0.51 eV Due to a Single Harmonic Voltage
Determine for an activation energy of E = 0.51 eV the slope E/K and for the additional temperature rise ΔTh = 3 = 6.6 °C (see Application Example 6.2 with Tamb = 40°, T2 = Trat = 100 °C) the reduced lifetime of a single-phase induction motor.
Solution to Application Example 6.4
The slope (E/K) is E/K = 5.91·103 kelvin. Thus one obtains from t1=40e−5.91⋅103▵Th/373(373+▵Th),![]() with ΔTh = 6.6 °C, a reduced lifetime of t1|▵Th=3=6.6°C=30.37years
with ΔTh = 6.6 °C, a reduced lifetime of t1|▵Th=3=6.6°C=30.37years![]() .
.
From Application Examples 6.3 and 6.4 one concludes that lower values of the activation energy E result in lower decreases in lifetime.
6.9 Reduction of lifetime of components with activation energy E = 1.1 eV due to harmonics of the terminal voltage within residential or commercial utility systems
Figure 6.14 shows the additional temperature rises (or losses) in percent of the rated temperature rises (or losses) as a function of the weighted-harmonic factor. These functions are obtained from calculations and measurements [18,19]. Note that the ambient temperature has been eliminated. For the evaluation of the reduction of the lifetime one must base all calculations on an activation energy of about E = 1.1 eV because of Fig. 6.16, which confirms that the majority of (insulation) materials have such a distinct activation energy.
According to Fig. 6.14, a weighted harmonic-voltage factor of hmax∑h=21hk(VphVp1)ℓ=5.8 corresponds to additional temperature rises (referred to the rated temperature rises) on the average of 6.2% for single-phase induction machines, 3.2% for three-phase induction machines, and 0.85% for transformers and universal machines. These percentage values confirm that single-phase machines are very sensitive to harmonic voltages due to their forward- and backward-rotating fields and their short-circuited rotor, three-phase induction machines are sensitive to voltage harmonics due to their short-circuited rotor, transformers are not very sensitive to voltage harmonics because of their resistive load, and universal machines are not sensitive as well because the commutator transforms a voltage source to a current source where the current magnitudes are limited. A weighted-harmonic voltage factor of 5.8 results for the rated temperature T2 = 85 °C at Tamb60Hz ≈ Tambh = 23 °C in temperature increases of 3.84 °C for single-phase induction machines, 1.98 °C for three-phase induction machines, and 0.53 °C for transformers and universal machines. With these additional temperature increases one obtains at an activation energy of E = 1.1 eV – with E/K = 12,769 kelvin – the decreased lifetime (using Eq. 6-32) of 31.5% for single-phase induction machines, 18% for three-phase induction machines, and 5% for transformers and universal machines.
corresponds to additional temperature rises (referred to the rated temperature rises) on the average of 6.2% for single-phase induction machines, 3.2% for three-phase induction machines, and 0.85% for transformers and universal machines. These percentage values confirm that single-phase machines are very sensitive to harmonic voltages due to their forward- and backward-rotating fields and their short-circuited rotor, three-phase induction machines are sensitive to voltage harmonics due to their short-circuited rotor, transformers are not very sensitive to voltage harmonics because of their resistive load, and universal machines are not sensitive as well because the commutator transforms a voltage source to a current source where the current magnitudes are limited. A weighted-harmonic voltage factor of 5.8 results for the rated temperature T2 = 85 °C at Tamb60Hz ≈ Tambh = 23 °C in temperature increases of 3.84 °C for single-phase induction machines, 1.98 °C for three-phase induction machines, and 0.53 °C for transformers and universal machines. With these additional temperature increases one obtains at an activation energy of E = 1.1 eV – with E/K = 12,769 kelvin – the decreased lifetime (using Eq. 6-32) of 31.5% for single-phase induction machines, 18% for three-phase induction machines, and 5% for transformers and universal machines.
Conclusion
It is believed that the weighted-harmonic voltage factor for single-phase and three-phase induction motors in the neighborhood of 5.8 represents a compromise which on the one hand promotes the installation of solid-state circuits by choosing generous permissible harmonic voltage levels, and on the other hand avoids severe detrimental reactions on the majority of the residential or commercial power system components including loads. Harmonic spectra of the residential or commercial power system voltage that satisfy for single-phase and three-phase induction motors
hmax∑h=21hk(VphVp1)ℓ≈5.8
result in acceptable temperature rises as far as induction motors, transformers, and universal machines are concerned. Thus it is recommended not to rigidly fix the harmonic voltages but rather the additional temperature rises they generate.
6.10 Possible limits for harmonic voltages
In order to illustrate the use of Eqs. 6-33 and 6-32, the harmonic voltage spectra for a single-phase and for a three-phase feeder (see Table 6.1) are proposed [33].
Table 6.1
Possible Voltage Spectra of Single-Phase and Three-Phase Feeders
| h | (VhV60Hz)1Φ(%) | (VhV60Hz)3Φ(%) |
| 1 | 100 | 100 |
| 2 | 0.5 | 0.5 |
| 3 | 4.0 | 2.0a |
| 4 | 0.3 | 0.5 |
| 5 | 3.0 | 5.0 |
| 6 | 0.2 | 0.2 |
| 7 | 2.0 | 3.5 |
| 8 | 0.2 | 0.2 |
| 9 | 1.0 | 0.3 |
| 10 | 0.1 | 0.1 |
| 11 | 1.5 | 1.5 |
| 12 | 0.1 | 0.1 |
| 13 | 1.5 | 1.0 |
| 14 | 0.1 | 0.05 |
| 15 | 0.5 | 0.1 |
| 16 | 0.05 | 0.05 |
| 17 | 1.0 | 0.5 |
| 18 | 0.05 | 0.01 |
| 19 | 1.0 | 0.5 |
| All higher harmonics < 0.5% |
a Under certain conditions (e.g., DC bias of transformers as discussed in Chapter 2, and the harmonic generation of synchronous generators as outlined in Chapter 4) triplen harmonics are not of the zero-sequence type and can therefore exist in a three-phase system.
With average values of kavg = 0.85 and ℓavg = 1.4 for single-phase induction motors, kavg = 0.95 and ℓavg = 1.6 for three-phase induction motors, kavg = 0.90 and ℓavg = 1.75 for single-phase and three-phase transformers, and kavg = 1.0 and ℓavg = 2.0 for universal machines, one obtains for the single-phase spectrum of Table 6.1 the weighted harmonic-voltage factor for single-phase induction motors hmax∑h=21hk(VphVp1)ℓ≈5.7 . For the three-phase spectrum of Table 6.1 one obtains for three-phase induction motors hmax∑h=21hk(VphVp1)ℓ≈5.7
. For the three-phase spectrum of Table 6.1 one obtains for three-phase induction motors hmax∑h=21hk(VphVp1)ℓ≈5.7 . For single-phase transformers hmax∑h=21hk(VphVp1)ℓ≈7.37
. For single-phase transformers hmax∑h=21hk(VphVp1)ℓ≈7.37 . For three-phase transformers hmax∑h=21hk(VphVp1)ℓ≈7.4
. For three-phase transformers hmax∑h=21hk(VphVp1)ℓ≈7.4 . For universal motors hmax∑h=21hk(VphVp1)ℓ≈8.5
. For universal motors hmax∑h=21hk(VphVp1)ℓ≈8.5 . Any other set of voltage harmonics is feasible if Eq. 6-33 is about satisfied. Based on Fig. 6.14 (with T2 = 85 °C, Tamb = 23 °C, E = 1.1 eV, and rated lifetime of t2 = 40 years), those harmonic factors result in the additional temperature rises and lifetime reductions of Table 6.2.
. Any other set of voltage harmonics is feasible if Eq. 6-33 is about satisfied. Based on Fig. 6.14 (with T2 = 85 °C, Tamb = 23 °C, E = 1.1 eV, and rated lifetime of t2 = 40 years), those harmonic factors result in the additional temperature rises and lifetime reductions of Table 6.2.
Table 6.2
Additional Temperature Rise and Associated Lifetime Reduction of Induction Motors, Transformers, and Universal Motors Due to the Harmonic Spectra of Table 6.1
| Single-phase induction motors | Three-phase induction motors | Single-phase transformers | Three-phase transformers | Universal motors | |
| ΔTh (%) | 6.2 | 3.2 | 1.2 | 1.2 | 1.3 |
| ΔTh (°C) | 3.84 | 1.98 | 0.74 | 0.74 | 0.81 |
| Lifetime reduction (%) | 31.5 | 17.8 | 7.1 | 7.1 | 7.7 |

6.10.1 Application Example 6.5: Estimation of Lifetime Reduction for Given Single-Phase and Three-Phase Voltage Spectra with High Harmonic Penetration with Activation Energy E = 1.1 eV
Estimate the lifetime reductions of induction machines, transformers, and universal machines for the single- and three-phase voltage spectra of Table E6.5.1 and their associated lifetime reduction for an activation energy of E = 1.1 eV. The ambient temperature is Tamb = 23 °C, the rated temperature is T2 = 85 °C, and the rated lifetime of t2 = 40 years can be assumed.
Solution to Application Example 6.5
Calculation of weighted harmonic factor for single-phase spectrum of Table E6.5.1 based on the values for kavg = 0.85 and ℓavg = 1.4 for single-phase induction motors:
120.85(2.5)1.4=2.000,130.85(5.71)1.4=4.506,140.85(1.6)1.4=0.594,…,1170.85(0.23)1.4=0.0115,1180.85(0.22)1.4=0.0103,1190.85(1.03)1.4=0.0853.
Summing all contributions results in the weighted harmonic-voltage factor for single-phase induction motors hmax∑h=21hk(VphVp1)ℓ≈8.5 .
.
Calculation of weighted harmonic factor for three-phase spectrum of Table E6.5.1 using the values for kavg = 0.95 and ℓavg = 1.6 for three-phase induction motors:
120.95(0.5)1.6=0.1707,130.95(1.0)1.6=0.3522,140.95(0.5)1.6=0.0884,…,1170.95(1.5)1.6=0.1297,1180.95(0.01)1.6=0.00004,1190.95(1.0)1.6=0.0609.
Summing all contributions results in the weighted harmonic-voltage factor for three-phase induction motors hmax∑h=21hk(VphVp1)ℓ≈8.6 .
.
Calculation of weighted harmonic factor for single-phase spectrum of Table E6.5.1 based on the values for kavg = 0.90 and ℓavg = 1.75 for single-phase transformers:
120.9(2.5)1.75=2.664,130.9(5.71)1.75=7.847,140.9(1.6)1.75=0.6536,…,1170.9(0.23)1.75=0.00597,1180.9(0.22)1.75=0.00524,1190.9(1.03)1.75=0.744.
Summing all contributions results in the weighted harmonic-voltage factor for single-phase transformers hmax∑h=21hk(VphVp1)ℓ≈12.3.
Calculation of weighted harmonic factor for three-phase spectrum of Table E6.5.1 based on the values for kavg = 0.90 and ℓavg = 1.75 for three-phase transformers:
120.9(0.5)1.75=0.1593,130.9(1)1.75=0.37203,140.9(0.5)1.75=0.0854,…,1170.9(1.5)1.75=0.15876,1180.9(0.01)1.75=0.0000234,1190.9(1)1.75=0.07065.
Summing all above contributions results in the weighted harmonic-voltage factor for three-phase transformers hmax∑h=21hk(VphVp1)ℓ≈11.8.
Calculation of weighted harmonic factor for single-phase spectrum of Table E6.5.1 based on the values for kavg = 1.0 and ℓavg = 2.0 for universal motors:
12(2.5)2=3.125,13(5.71)2=10.868,14(1.6)2=0.640,....,117(0.23)2=0.00311,118(0.22)2=0.0027,119(1.03)2=0.0558.
Summing all contributions results in the weighted harmonic-voltage factor for universal motors hmax∑h=21hk(VphVp1)ℓ≈15.6.
Based on Fig. 6.14, T2 = 85 °C, Tamb = 23 °C, E = 1.1 eV, and rated lifetime of t2 = 40 years the above harmonic factors result in the additional temperature rises and lifetime reductions of Table E6.5.2.
Table E6.5.2
Additional Temperature Rise and Associated Lifetime Reduction of Induction Motors, Transformers, and Universal Motors Due to the Harmonic Spectra of Table E6.5.1
| Single-phase induction motors | Three-phase induction motors | Single-phase transformers | Three-phase transformers | Universal motors | |
| ΔTh (%) | 9.2 | 4.5 | 1.9 | 1.8 | 2.4 |
| ΔTh (°C) | 5.7 | 2.8 | 1.2 | 1.1 | 1.5 |
| Lifetime reduction (%) | 43 | 24 | 11 | 10 | 14 |

6.10.2 Application Example 6.6: Estimation of Lifetime Reduction for Given Single-Phase and Three-Phase Voltage Spectra with Moderate Harmonic Penetration with Activation Energy E = 1.1 eV
Estimate the lifetime reductions for induction machines, transformers, and universal machines for the single- and three-phase voltage spectra of Table E6.6.1 and their associated lifetime reduction for an activation energy of E = 1.1 eV. The ambient temperature is Tamb = 23 °C, the rated temperature is T2 = 85 °C, and the rated lifetime of t2 = 40 years can be assumed.
Solution to Application Example 6.6
Calculation of weighted harmonic factor for single-phase spectrum of Table E6.6.1 based on the values for kavg = 0.85 and ℓavg = 1.4 for single-phase induction motors:
120.85(0.5)1.4=0.2103,130.85(3)1.4=1.8297,140.85(0.3)1.4=0.05703,....,1170.85(0.5)1.4=0.0341,1180.85(0.05)1.4=0.0013,1190.85(0.4)1.4=0.0227.
Summing all contributions results in the weighted harmonic-voltage factor for single-phase induction motors hmax∑h=21hk(VphVp1)ℓ≈3.4 .
.
Calculation of weighted harmonic factor for three-phase spectrum of Table E6.6.1 using the values for kavg = 0.95 and ℓavg = 1.6 for three-phase induction motors:
120.95(0.5)1.6=0.1707,130.95(0.5)1.6=0.1162,140.95(0.5)1.6=0.0884,....,1170.95(0.3)1.6=0.00986,1180.95(0.01)1.6=0.00004,1190.95(0.2)1.6=0.00464.
Summing all contributions results in the weighted harmonic-voltage factor for three-phase induction motors hmax∑h=21hk(VphVp1)ℓ≈2.6.
Calculation of weighted harmonic factor for single-phase spectrum of Table E6.6.1 based on the values for kavg = 0.90 and ℓavg = 1.75 for single-phase transformers:
120.90(0.5)1.75=0.1593,130.90(0.3)1.75=2.544,140.90(0.3)1.75=0.0349,....,1170.90(0.5)1.75=0.0232,1180.90(0.05)1.75=0.000392,1190.90(0.4)1.75=0.01421.
Summing all contributions results in the weighted harmonic-voltage factor for single-phase transformers hmax∑h=21hk(VphVp1)ℓ≈4.1.
Calculation of weighted harmonic factor for three-phase spectrum of Table E6.6.1 based on the values for kavg = 0.90 and ℓavg = 1.75 for three-phase transformers:
120.90(0.5)1.75=0.1593,130.90(0.5)1.75=0.1106,140.90(0.5)1.75=0.0854,....,1170.90(0.3)1.75=0.00949,1180.90(0.05)1.75=0.0000234,1190.90(0.2)1.75=0.00423.
Summing all contributions results in the weighted harmonic-voltage factor for three-phase transformers hmax∑h=21hk(VphVp1)ℓ≈3.1.
Calculation of weighted harmonic factor for single-phase spectrum of Table E6.6.1 based on the values for kavg = 1.0 and ℓavg = 2.0 for universal motors:
12(0.5)2=0.125,13(3)2=3.0,14(0.3)2=0.0225,…,117(0.5)2=0.0147,118(0.05)2=0.000139,119(0.4)2=0.00842.
Summing all contributions results in the weighted harmonic-voltage factor for universal motors:
hmax∑h=21hk(VphVp1)ℓ≈4.4.
Based on Fig. 6.14 the above harmonic factors, T2 = 85 °C, Tamb = 23 °C, E = 1.1 eV, and rated lifetime of t2 = 40 years result in the additional temperature rises and lifetime reductions of Table E6.6.2.
Table E6.6.2
Additional Temperature Rise and Associated Lifetime Reduction of Induction Motors, Transformers, and Universal Motors Due to the Harmonic Spectra of Table E.6.6.1
| Single-phase induction motors | Three-phase induction motors | Single-phase transformers | Three-phase transformers | Universal motors | |
| ΔTh (%) | 3.7 | 1.3 | 0.6 | 0.4 | 0.7 |
| ΔTh (°C) | 2.3 | 0.81 | 0.37 | 0.25 | 0.43 |
| Lifetime reduction (%) | 20 | 7.7 | 3.6 | 2.5 | 4.2 |

6.11 Probabilistic and time-varying nature of harmonics
As mentioned in Section 6.1, the harmonic current or voltage spectra within a distribution feeder are continually changing as a function of changes in the load and the system’s condition. The rationale given for using the worst-case conditions, where loads are operating for at least a few hours at rated operation generating the “rated current/voltage spectra,” is the basis for the IEEE [35] and IEC [36] harmonic guidelines and standards, respectively. Nevertheless it will be worthwhile to study the time-varying nature [37,38] of harmonic spectra. In these publications continually changing current (THDi) and voltage (THDv) total harmonic distortions are plotted as a function of time. They indeed change widely from 2.5% to about 9% for THDi, and from 1% to about 5% for the THDv for one site, and for another site the changes are similar in magnitude. As mentioned in prior sections, the THDs are neither a good measure for temperature rises nor for vibrations; instead harmonic components should be used in any further studies. The measured THD data are characterized by statistical measures (e.g., minimum, maximum, average or mean values, standard deviation, probability distribution), histograms or probability density functions (pdf), probability distribution functions (PX(x)), statistical description of sub-time intervals, and combined deterministic or statistical description [41–45]. These publications address the harmonic summation and propagation by explaining the sum of random harmonic phasors via the representation of harmonic phasors, marginal pdf of x–y components, pdf of sum of projections of independent phasors, and pdf of magnitude of sum of random phasors. These papers apply the methods described to a 14-bus transmission system and provide general guidelines with respect to their applicability. The probabilistic evaluation of the economic cost due to harmonic losses in industrial energy systems is presented in the next section.
6.12 The cost of harmonics
The cost of harmonics can originate either in
• the complicated solid-state components necessary to maintain the current or voltage harmonics at a low level, for example, switched-mode power supplies operating at unity-power factor [39], or in
• the use of simple peak-rectifiers resulting in high harmonic amplitudes [40].
Both costs are not negligibly small and must be considered in the future. The first approach appears to be favored by the IEC [36] for low-, medium-, and high-voltage power systems, whereas the latter appears to be favored by IEEE [35] for single-phase systems only.
In references [41–45] the cost of the latter approach is discussed by defining the economic damage (cost) due to harmonic losses D = Dw + Da, where Dw is the operating cost and Da is the aging cost. This economic damage is a probabilistic quantity because the harmonic voltage or current spectra change in a random manner. The expected value of these costs is defined as E(D) = E(Dw) + E(Da), where E(Dw) is the present-worth expected value of the operating costs due to harmonic losses and E(Da) is the present-worth expected value of the aging costs due to harmonic losses. Numerical results for a 20 kV, 150 MVA industrial feeder illustrate that the economic damage for induction motors is significant and within a lifetime of 35 years amounts to about the purchase cost ($7,625) of an induction motor.
6.13 Temperature as a function of time
Rotating machines, transformers, and inductors must be designed so that their rated temperatures will not be exceeded. For rotating machines the maximum torques are not a design criterion as long as the machines continue to operate. The maximum permissible temperature (hot spot) must not be exceeded, otherwise the lifetime will be reduced. Note that any machine works most efficiently and cost-effectively if the permissible (maximum) rated temperature will be reached but not exceeded at any time. At steady-state machines must be able to operate at rated torque. For a short time machines can be operated above rated torque. This leads to the concept of intermittent operation discussed in a later section.
A motor can be replaced by a radiating sphere as illustrated in Fig. 6.17. During a small time increment dt one can assume that the temperature of the sphere increases by the incremental temperature dθ. For this reason the change in stored heat (increase) dQC during the time dt is
dQC=C⋅dθ,
where θ is the temperature rise and C is the heat-absorption capacity. Note that Eq. 6-34 is independent of time.

Due to thermal radiation a part of the stored heat will be emitted to the surrounding environment. The change of the stored heat (reduction) dQA is time dependent:
dQA=A⋅θ⋅dt,
where A is the heat-radiation capacity.
The sum of Eqs. 6-34 and 6-35 yields the ordinary differential equation
dQ=dQC+dQA=C⋅dθ+A⋅θ⋅dt=Ploss⋅dt,
where Ploss · dt is the (loss) energy absorbed by the machine during the incremental time dt. Dividing Eq. 6-36 by dt and A, one obtains the first-order ordinary differential equation
PlossA=CA⋅dθdt+θ=τθ⋅dθdt+θ,
where τθ = (C/A) is the thermal time constant. The solution of this first-order differential equation is
θ=PlossA+k⋅e(−t/τθ).
For t = 0 and θ = θo (initial temperature rise) and for t = ∞ with θ = θf = Ploss/A (final temperature rise) one obtains for the temperature as a function of time
θ=θf−(θf−θo)⋅e(−t/τθ).
Figure 6.18 illustrates the solution of Eq. 6-39 including its time constant. The temperature transient during a load cycle is schematically depicted in Fig. 6.19 with θf = Ploss/A.


6.13.1 Application Example 6.7: Temperature Increase of Rotating Machine with a Step Load
An enclosed fan-cooled induction motor has a thermal time constant of τθ = 3 h and a steady-state rated temperature of θf = 120 °C at an ambient temperature of θamb = 40 °C. The motor has at time t = 0- a temperature of θ = θamb, and the motor is fully loaded at t = 0+. Calculate the time t95% when the fully loaded motor reaches 95% of its final temperature θf = 120 °C.
Solution to Application Example 6.7
With Eq. 6-39 one obtains
0.95⋅θf=θf−(θf−θamb)e(−t95%τθ),
0.95⋅120=(120−40)e(−t95%τθ),
or t95%=2.59⋅τθ=7.77h.![]()
6.14 Various operating modes of rotating machines
Depending on their applications, rotating machines can be subjected to various operating modes such as steady-state, short-term, steady-state with short-term, intermittent, and steady-state with intermittent operating modes.
6.14.1 Steady-State Operation
Steady-state temperature is reached when the operating time of the machine toper is large as compared with the time constant τθ of the machine. That is,
toper≥(3−4)⋅τθ.
According to experience the thermal time constant for openly ventilated machines is
τθ≈1h
and for enclosed but ventilated machines
τθ≈(3−4)h.
During steady-state operation the rated output power must be delivered by the machine.
6.14.2 Short-Term Operation
For short-term operation one assumes that the machine cools down to the ambient temperature and its temperature rise (initial temperature rise) is θo = 0. Fig. 6.20 illustrates the transient temperature of this operating mode.

The absence of any ventilation during standstill (time tstandstill) requires that the time constant during standstill be longer than that during operation (time toper), that is, τstandstul > τoper. For short-term operation the times toper and tstandstill must relate to the time constants as follows:
toper<(3−4)τoper,
tstandstill<(3−4)τstandstill.
The transient temperature is for short-term operation (see Fig. 6.20):
θshort-term=θrated=θshort-term_final[1−e(−toperτoper)].
The final short-term temperature is obtained from Eq. 6-45:
θshort-term_final=θrated/[1−e(−toperτoper)],
with
θshort–term_final∝Ploss_short-term
and
θrated∝Ploss_rated.
It follows for the losses during short-term operation:
Ploss_short-term=Ploss_rated/[1−e(−,toperτoper)].
For machines whose losses consist of iron-core and copper losses (e.g., induction machines) the total losses at rated operation are
Ploss_rated=p·Prated+q·Prated.
The first term of Eq. 6-50 pertains to the iron-core and the second term to the copper losses. The losses during short-term operation are
Ploss_short-term=p⋅Prated+q⋅Prated(Ploss_short-termPrated)2.
Introducing Eqs. 6-50 and 6-51 into Eq. 6-49 yields the ratio
Ploss_short-termPrated=√[1+pq]{1/[1−e(toperτoper)]}−pq,
where the ratio p/q is available from the manufacturer of the machine.
6.14.3 Steady State with Short-Term Operation
In this case the short-term load is superposed with the steady-state load (see Fig. 6.21). The operating time toper and the pause time tpause relate to the time constant as follows:
toper<(3−4)⋅τθ,
tpause>(3−4)⋅τθ,
and the ratio between the required power during steady-state with short-term load to the rated power is
Psteady-state+short-timePrated=√{1/[1−e(toperτθ)]}.

In Eq. 6-55 the iron-core losses are neglected (p = 0).
6.14.4 Intermittent Operation
The mode of intermittent operation occurs most frequently. One can differentiate between two cases:
• irregular load steps (see Fig. 6.22), and

• regular load steps.
The case with irregular load steps is discussed in Application Example 6.8.
The case with regular load steps can be approximated as follows based on Fig. 6.23:
PintermittentPrated=√(1+pq)(1+tpausetoper⋅τθτstandstill)−pq.

6.14.5 Steady State with Intermittent Operation
Steady state with superimposed periodic intermittent operation (see Fig. 6.24) does not occur frequently. The ratio between the power required for this case and the rated power is
Psteady-state+periodicintermittentPrated=√(1+tpausetoper)
for toper < (3–4) τθ and tpause < (3–4) τθ. In summary one can state that for the motor sizing the maximum temperature (and not the torque) is important.

Intermittent operation occurs in drives such as used in hybrid cars, wind-power plants, air-conditioning and refrigeration systems, and others. For this reason a detailed analysis of steady state with superposed intermittent operation will be presented in Application Example 6.8.
6.14.6 Application Example 6.8: Steady State with Superimposed Periodic Intermittent Operation with Irregular Load Steps
A three-phase, squirrel-cage induction motor is fed by a voltage-source inverter. The induction motor is operated at variable frequency and constant (rated) flux (that is, |˜E|/f=constant![]() ) and has the following nameplate data: VL-L = 460 V, f = 60 Hz, p = 4 poles, nm_rat = 1720 rpm, Pout_rat = 29.594 kW or 39.67 hp. The stator winding is Y-connected, and the parameters per phase are Rs = 0.5 Ω, Rʹr = 0.2 Ω, Xs = Xʹr = 1 Ω, Xm = 30 Ω at f = 60 Hz, and Rfe → ∞. The axial moment of inertia of the motor is Jm = 0.234 kgm2, the viscous damping coefficient B can be assumed to be zero, and the inertia of the load referred to the motor shaft is Jload = 4.766 kgm2. The steady-state/intermittent load cycle is shown in Fig. E6.8.1.
) and has the following nameplate data: VL-L = 460 V, f = 60 Hz, p = 4 poles, nm_rat = 1720 rpm, Pout_rat = 29.594 kW or 39.67 hp. The stator winding is Y-connected, and the parameters per phase are Rs = 0.5 Ω, Rʹr = 0.2 Ω, Xs = Xʹr = 1 Ω, Xm = 30 Ω at f = 60 Hz, and Rfe → ∞. The axial moment of inertia of the motor is Jm = 0.234 kgm2, the viscous damping coefficient B can be assumed to be zero, and the inertia of the load referred to the motor shaft is Jload = 4.766 kgm2. The steady-state/intermittent load cycle is shown in Fig. E6.8.1.

The induction motor is operated at 60 Hz (natural torque-speed characteristic).
a) Determine the rated synchronous speed, rated synchronous angular velocity, rated angular velocity, rated slip, rated stator current |˜Is|![]() , rated rotor current |Ĩr′|, and rated induced voltage |Ẽ|.
, rated rotor current |Ĩr′|, and rated induced voltage |Ẽ|.
b) Calculate the maximum torque Tmax at sm and the fictitious maximum torque Tmax_fict at s = 1.
c) Derive from the equation of motion the slip s(t) as a function of the initial slip s(0), the load torque TL(t), the maximum fictitious torque Tmax_fict, the time constant τm, and the time t.
d) Apply the solution for s(t) to the different regions of Fig. E6.8.1 and plot s(t) from t = 0 to the maximum time t = 5 s of the load-cycle time period of Tperiod = 5 s.
e) Calculate the torque T(t) and plot it from t = 0 to t = 5 s.
f) Based on the slip function compute pointwise the stator current |Ĩs(t)| and plot |Ĩs(t)| from t = 0 to t = 5 s.
g) Plot |Ĩs(t)|2 as a function of time from t = 0 to t = 5 s.
h) Determine the rms value of the motor (stator) current is(t) for the entire load cycle as specified in Fig. E6.8.1; that is, determine
Is_rms=√1Tt+T∫t|˜Is(t)|2dt.
i) Is this induction motor over- or underdesigned? If it is underdesigned, what is the reduction of lifetime?