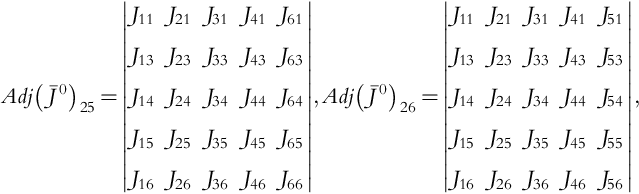Solution to Application Example 7.11
Calculation of the inverse of ![]() , that is.
, that is. ![]() .
.
where Adj ![]() is the adjoint of matrix
is the adjoint of matrix ![]() and det
and det![]() = |
= |![]() | is the determinant of
| is the determinant of ![]() .
.
The adjoint of ![]() is obtained by first taking the transpose of
is obtained by first taking the transpose of ![]() , that is,
, that is, ![]() , and then replacing each element in the transpose with its cofactor:
, and then replacing each element in the transpose with its cofactor:
The transpose of ![]() is
is
where
As an example, the calculation of the first entry of the adjonint Adj![]() will be outlined:
will be outlined:
The determinant is
The ![]() entry is now
entry is now![]() .
.
7.3.9 Application Example 7.12: Inversion of a 3 × 3 Matrix
In order to demonstrate the entire procedure for the computation of the inverse of a matrix the following 3 × 3 matrix will be used
Solution to Application Example 7.12
Transpose of Ā is
The cofactors of Āt are
The determinant det![]() is
is
The inverse of Ā is now
7.3.10 Application Example 7.13: Computation of the Correction Voltage Vector
For the system of Fig. E7.8.1, compute the correction voltage vector![]() , updating the mismatch power vector, and check the convergence of the load flow algorithm (using a convergence tolerance of 0.0001).
, updating the mismatch power vector, and check the convergence of the load flow algorithm (using a convergence tolerance of 0.0001).
Solution to Application Example 7.13
Based on the results of Application Examples 7.9 to 7.11, the correction voltage vector ![]() can be computed from
can be computed from
The updated mismatch power vector is
Since the components of ![]() are larger than the specified convergence tolerance (e.g., 0.0001), the Newton–Raphson solution has not converged. However, it will converge in two iterations:
are larger than the specified convergence tolerance (e.g., 0.0001), the Newton–Raphson solution has not converged. However, it will converge in two iterations:
Fundamental power flow iteration summary (Fig. E7.8.1):
| Absolute real power mismatch | Absolute reactive power mismatch | |||||
| Iteration | Average (%) | Worst (%) | Worst bus | Average (%) | Worst (%) | Worst bus |
| 0 | 11.67 | 25 | 4 | 6.67 | 10.00 | 4 |
| 1 | 0.05 | 0.12 | 4 | 0.03 | 0.06 | 4 |
| 2 | 0.00 | 0.00 | 4 | 0.00 | 0.00 | 4 |

Fundamental power flow output solution (Fig. E7.8.1), where δ angles are rounded (approximate) values:
| Bus voltage | Bus generation (G) and load (L) powers | Line powera | |||||||
| From bus | |V| (%) | δ (°) | PG (%) | QG (%) | PL (%) | QL (%) | To bus | Pline (%) | Qline (%) |
| 1 | 100.0 | 0.00 | 35.09 | 20.15 | 0.00 | 0.00 | 2 | 13.35 | 10.69 |
| 4 | 21.73 | 9.47 | |||||||
| 2 | 99.76 | –0.02 | 0.00 | 0.00 | 10.00 | 10.00 | 1 | –13.32 | –10.66 |
| 3 | 3.32 | 0.66 | |||||||
| 3 | 99.64 | –0.16 | 0.00 | 0.00 | 0.00 | 0.00 | 2 | –3.32 | –0.65 |
| 4 | 3.32 | 0.65 | |||||||
| 4 | 99.59 | –0.20 | 0.00 | 0.00 | 25.00 | 10.00 | 3 | –3.32 | –0.65 |
| 1 | –21.68 | –9.35 | |||||||

a Active and reactive powers in the line between “from bus” and “to bus.”
7.4 Newton-based harmonic power flow
Classifications of solution approaches for the harmonic power (load) flow problem are summarized at the end of this chapter. In this section, the Newton-based harmonic power flow [5,6] is selected, analyzed, and thoroughly illustrated. There are two main reasons for this selection:
• The Newton-based harmonic power flow is relatively easy to understand and to implement since it is an extension of the conventional fundamental Newton–Raphson formulation; it is based on similar terminologies and equations. It is capable of including any type of nonlinear load assuming its v–i characteristic is available in the frequency (or time) domain.
• It was the first proposed approach for power system modeling with nonlinear loads and harmonic couplings [5,6].
Among the limitations of the Newton-based harmonic power flow in its present form is the assumption of balanced network and load conditions.
7.4.1 Harmonic Bus Admittance Matrix and Power Definitions
For nonsinusoidal operating conditions power system matrices will be defined at harmonic frequencies. These matrices include the harmonic bus admittance matrix ![]() the harmonic bus impedance matrix
the harmonic bus impedance matrix ![]() =
= ![]() , and the harmonic Jacobian
, and the harmonic Jacobian ![]() matrix.
matrix.
The harmonic bus admittance matrix ![]() is identical to the fundamental bus admittance matrix
is identical to the fundamental bus admittance matrix ![]() with the difference that line admittances are evaluated at the hth harmonic frequency fh = h · f1:
with the difference that line admittances are evaluated at the hth harmonic frequency fh = h · f1:
where ωh = 2πhf1 = h · 377 rad/s.
Power Definitions at Harmonic Frequencies
Consider a voltage v(t) and a current i(t) expressed in terms of their rms harmonic components
Then
• the active (real, average) power is given by
• the reactive power is given by
• and the apparent (voltampere) power is
In case of sinusoidal v(t) and i(t) (h = 1 only), we have
For nonsinusoidal cases that relation does not hold and must be replaced by
where D is called the distortion power. Other definitions have also been proposed for harmonic powers, which are not discussed here.
Classification of Time Harmonics
Time harmonics can be classified into three types (Table 7.2):
Table 7.2
Classification of Time Harmonics
| Positive (+) sequence | Negative (–) sequence | Zero (0) sequence |
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 10 | 11 | 12 |
| 13 | 14 | 15 |
| 16 | 17 | 18 |
| 19 | 20 | 21 |
• positively rotating harmonics (+),
• negatively rotating harmonics (–), and
• zero-sequence harmonics (0).
Triplen (multiples of three) harmonics (3h, for h = 1, 2, 3, …) in a balanced three-phase system are predominantly of the zero-sequence type. With a few exceptions (discussed in preceding chapters), zero-sequence currents cannot flow from the network into a delta or an ungrounded wye-connected device (e.g., transformer), and therefore triplen harmonics are excluded from this analysis.
7.4.2 Modeling of Nonlinear and Linear Loads at Harmonic Frequencies
Before proceeding with the reformulation of the Newton–Raphson load flow to include harmonic frequencies, it is necessary to properly model linear and nonlinear loads at fundamental and harmonic frequencies.
Harmonic Modeling of Nonlinear Loads
The (v–i) relationship of nonlinear loads (such as line-commutated converters) will be modeled as coupled harmonic current sources. The injected harmonic currents of a nonlinear load (Iinjected(h)) at bus m will be a function of its fundamental and harmonic voltages:
where αm and βm are the nonlinear load control parameters and L is the maximum harmonic order considered L = hmax. The currents of Eq. 7-91 are referred to the nonlinear bus m to which the nonlinear load is connected. The nonlinearity of ![]() is due to strong couplings between harmonic currents and voltages dictated by the nonlinear load. In some cases (e.g., decoupled harmonic power flow formulation), it is convenient to ignore harmonic couplings
is due to strong couplings between harmonic currents and voltages dictated by the nonlinear load. In some cases (e.g., decoupled harmonic power flow formulation), it is convenient to ignore harmonic couplings ![]() and simplify the problem.
and simplify the problem.
As an example, for a full-wave bridge rectifier connected to bus m (shown in Fig. 7.13), αm is the firing angle of semiconductor-controlled rectifiers (SCRs), and βm is either the commutating impedance (inductance) or the DC voltage (E). Note that the equivalent circuit models a three-phase full-wave rectifier/inverter with a general load, where Lcom is the commutating inductance, that is, the leakage inductance of the transformer, and

• for a passive load, only resistance R and filter inductance F are considered,
• for a DC motor drive, only R and E are considered (E > 0) when motoring, and
• for inverter operation with a DC generator, only R and E are considered (E < 0).
Modeling Linear Loads at Harmonic Frequencies
For the formulation of harmonic power flow, equivalent circuits of linear loads are required. At the fundamental frequency, linear loads are modeled as conventional PQ and PV buses. However, shunt admittances are used to model them at harmonic frequencies [7,8]. The admittance of a linear load connected to bus k at the hth harmonic is
where j represents the operator ![]() .
.
Capacitor banks are modeled as a fixed shunt reactance. Transformers are approximated by linear leakage inductances, and their nonlinearities and losses due to eddy currents, hysteresis, and saturation are neglected.
7.4.3 The Harmonic Power Flow Algorithm (Assembly of Equations)
Power system components, loads, and generators that produce time harmonics in an otherwise harmonic-free network are termed nonlinear. Other buses such as the standard PQ and PV buses with no converter or other nonlinear devices connected are termed linear. Consider
• Bus 1 to be the conventional swing (slack) bus with specified values for voltage magnitude |![]() | and phase angle δ1.
| and phase angle δ1.
• Buses 2 through (m – 1) to be the conventional linear PQ (or PV) buses. As with the conventional power flow problem, active Pi(1) and reactive Qi(1) powers are assumed to be known at these linear buses.
• Buses m through n to be nonlinear buses. At these buses, the fundamental real power Pi(1) and the total apparent power Si,total (or the total reactive power Qi,total) are specified.
Network voltages and currents are represented by Fourier series components, and the bus voltage vector ![]() of the fundamental power flow (Eq. 7-42) is redefined as
of the fundamental power flow (Eq. 7-42) is redefined as
where (superscripts and subscripts denote harmonic orders and bus numbers, respectively)
Harmonic bus voltage magnitudes, phase angles, and the nonlinear device parameters (αm, βm) are unknowns; therefore the conventional formulation (forcing the fundamental mismatch powers to zero) is not sufficient to solve the harmonic power flow problem. Three additional relations are used:
• Kirchhoff’s current law for the fundamental frequency (fundamental current balance) at nonlinear buses.
• Kirchhoff’s current law for each harmonic (harmonic current balance) at all buses.
• Conservation of apparent voltamperes (apparent power or voltampere balance) at nonlinear buses.
Note that Kirchhoff’s current law for the fundamental frequency is not applied to linear buses since active and reactive power (mismatch power) balance has already been applied at these buses.
Current Balance for Fundamental Frequency
The current balance is written for fundamental frequency (h = 1) at the nonlinear buses as indicated in Fig. 7.14, where the nonlinear currents gr,m(1), gi,m(1) are referred to bus m. Therefore one obtains for the nonlinear buses (from bus m to bus n) for the fundamental current balance:
where Ir,m(1) and Ii,m(1) are the fundamental real and reactive line currents at the mth nonlinear bus, respectively, and gr,m(1) and gi,m(1) are the fundamental real and reactive injected load currents at the same bus. Note that the line and injected load currents are positive if they leave the bus.

 at a nonlinear bus.
at a nonlinear bus.Current Balance at Harmonic Frequencies
For all (linear and nonlinear) buses one can write
The line currents Ir,m(h) and Ii,m(h) will be computed in the next section.
Apparent Power or Voltampere Balance
The third type of relation is the apparent power (voltampere) balance at each nonlinear bus j:
where j = m, …, n and
are the total (fundamental plus harmonics) real and reactive load powers at nonlinear buses. Dm to Dn can be computed from gr,m, gi,m, …, gr,n, gi,n; therefore, distortion powers are not independent variables. Equation 7-98 is used to update (between iterations) the nonlinear-device injected powers P and Q at the nonlinear buses.
The number of unknowns for the n buses are as follows (K = number of harmonics considered not including fundamental, e.g., for h = 1, 5, 7, 11 we get K = 3):

The number of available equations are as follows:

There remain 2(n – m + 1) equations to be defined. These can be the total real and reactive mismatch powers at the n – (m – 1) nonlinear buses:
where j = m, …, n and Pjt and Qjt are the total (fundamental and harmonics) nonlinear load real and reactive powers at bus j, respectively. ![]() and
and ![]() (for h = 1, 5, 7, …, L) are the total real and reactive line powers, respectively. Note that the formulas for Fr,j(h) and Fi,j(h) are identical to those for Fr,j and Fi,j of the fundamental power flow problem with the difference that
(for h = 1, 5, 7, …, L) are the total real and reactive line powers, respectively. Note that the formulas for Fr,j(h) and Fi,j(h) are identical to those for Fr,j and Fi,j of the fundamental power flow problem with the difference that ![]() and the hth harmonic voltages must be used. The application of the newly defined mismatch powers at the nonlinear buses results in 2(n – m + 1) additional equations, and the number of equations is identical to the number of unknowns.
and the hth harmonic voltages must be used. The application of the newly defined mismatch powers at the nonlinear buses results in 2(n – m + 1) additional equations, and the number of equations is identical to the number of unknowns.
7.4.4 Formulation of Newton–Raphson Approach for Harmonic Power Flow
The mismatch vector (consisting of mismatch power and mismatch currents) for harmonic power flow is defined as
where Δ![]() is the mismatch power vector (Eq. 7-56) and (ΔĪ(5), …, ΔĪ(L), ΔĪ(1)) is the mismatch current vector for the harmonics including the fundamental.
is the mismatch power vector (Eq. 7-56) and (ΔĪ(5), …, ΔĪ(L), ΔĪ(1)) is the mismatch current vector for the harmonics including the fundamental.
In Eq. 7-101,
where ![]() applies to linear buses, and ΔPmnonlinear, ΔQmnonlinear, …, ΔPnnonlinear, ΔQnnonlinear applies to nonlinear buses. Pj(1) and Qj(1) are the real and reactive fundamental load powers for the linear bus j (as defined by the fundamental load flow analysis), respectively; Fr,j(1) and Fi,j(1) are the (line) fundamental real and reactive powers at the linear bus j (see fundamental load flow analysis), respectively.
applies to linear buses, and ΔPmnonlinear, ΔQmnonlinear, …, ΔPnnonlinear, ΔQnnonlinear applies to nonlinear buses. Pj(1) and Qj(1) are the real and reactive fundamental load powers for the linear bus j (as defined by the fundamental load flow analysis), respectively; Fr,j(1) and Fi,j(1) are the (line) fundamental real and reactive powers at the linear bus j (see fundamental load flow analysis), respectively.
The fundamental current mismatch is defined for nonlinear buses where all currents (e.g., line currents and nonlinear load currents) are referred to the swing bus:
and the harmonic current mismatch is defined for linear and nonlinear buses including swing bus:
where the nonlinear load current components Gr,m(h) and Gi,m(h) are given (referred to swing bus) and the line current components Ir,m(h) and Ii,m(h) will be generated in the next section. The Newton–Raphson method is implemented by forcing the appropriate mismatches, Δ![]() , to zero using the Jacobian matrix
, to zero using the Jacobian matrix ![]() and obtaining appropriate correction terms
and obtaining appropriate correction terms ![]() , where ξ represents the iteration number:
, where ξ represents the iteration number:
The Jacobian ![]() is a 2(nK + n – 1) + 2(n – m + 1) by 2(nK + n – 1) + 2(n – m + 1) matrix, where n is the total number of buses, (m – 1) is the number of linear buses including the swing bus, and K is the number of harmonics considered, excluding the fundamental (h = 1):
is a 2(nK + n – 1) + 2(n – m + 1) by 2(nK + n – 1) + 2(n – m + 1) matrix, where n is the total number of buses, (m – 1) is the number of linear buses including the swing bus, and K is the number of harmonics considered, excluding the fundamental (h = 1):
Solving the equation for the correction vector yields
where all elements in this matrix equation are subvectors and submatrices partitioned from Δ![]() and ΔŪ(ζ).
and ΔŪ(ζ).
The subvectors are
• ![]() = mismatch power vector at all buses except the swing bus,
= mismatch power vector at all buses except the swing bus,
• ΔĪ(1) = fundamental mismatch current vector at nonlinear buses, and
• ΔĪ(h) = hth harmonic mismatch current vector at all buses.
The submatrices are
• ![]() = Jacobian 2(n – 1) square matrix corresponding to Jacobian of fundamental power flow written for all buses except the swing bus, and
= Jacobian 2(n – 1) square matrix corresponding to Jacobian of fundamental power flow written for all buses except the swing bus, and
• ![]() = Jacobian of harmonic h ≠ 1 with dimensions 2(n – 1) × 2n, whereby there are zero entries for (m – 1) linear buses:
= Jacobian of harmonic h ≠ 1 with dimensions 2(n – 1) × 2n, whereby there are zero entries for (m – 1) linear buses:
where ![]() denotes a 2(m – 2) by 2n array of zeros and
denotes a 2(m – 2) by 2n array of zeros and ![]() is a 2(n – 1) by 2n matrix.
is a 2(n – 1) by 2n matrix.
The partial derivatives are found using the harmonic admittance matrix ![]() and the harmonic voltages:
and the harmonic voltages:
or
• ![]() is an array of partial derivatives of the hth harmonic (linear) line currents with respect to the hth harmonic bus voltages,
is an array of partial derivatives of the hth harmonic (linear) line currents with respect to the hth harmonic bus voltages,
• ![]() is an array of partial derivatives of the hth (nonlinear) harmonic load currents with respect to the hth harmonic bus voltages, and
is an array of partial derivatives of the hth (nonlinear) harmonic load currents with respect to the hth harmonic bus voltages, and
• ![]() is an array of partial derivatives of the hth harmonic nonlinear load currents with respect to the jth harmonic bus voltages:
is an array of partial derivatives of the hth harmonic nonlinear load currents with respect to the jth harmonic bus voltages:
where the partial derivatives of Gr,m(h) and Gi,m(h) are referred to the swing bus. Note that ![]() is a 2n square matrix; however, for h = 1 only the last 2(n – m + 1) rows exist because the fundamental current balance is not applied to linear buses.
is a 2n square matrix; however, for h = 1 only the last 2(n – m + 1) rows exist because the fundamental current balance is not applied to linear buses. ![]() is a 2(n – m + 1) × 2n matrix and for j = 1 the first two columns do not exist because
is a 2(n – m + 1) × 2n matrix and for j = 1 the first two columns do not exist because ![]() and δ1(1) are known, that is,
and δ1(1) are known, that is, ![]() is a 2n × 2(n – 1) matrix.
is a 2n × 2(n – 1) matrix.
![]() is an array of partial derivatives of real and imaginary nonlinear load currents with respect to the firing angle α and the commutation impedance β:
is an array of partial derivatives of real and imaginary nonlinear load currents with respect to the firing angle α and the commutation impedance β: