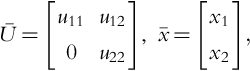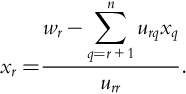Power System Modeling under Nonsinusoidal Operating Conditions
Abstract
Presents power system modelling under non-sinusoidal operating conditions. It includes review of power system matrices, triangular factorization, and forward- and backward- substitutions. Thereafter, the Newton-Raphson fundamental load flow algorithm, power-system matrices at harmonic frequencies, and the Newton-Raphson harmonic power flow formulation are presented. Subsequently, a survey and classification of harmonic power flow approaches are given. 19 application examples with solutions are presented, and 8 application-oriented problems are included.
The calculation of power system harmonic voltages and currents and analyzing power quality problems can be classified into frequency- and time-domain methods. Frequency-domain techniques are widely used for harmonic problem formulation. They are a reformulation of the fundamental load flow problem in the presence of nonlinear loads and/or distorted utility voltages. This complicated, nonlinear, and harmonically coupled problem has been solved in several ways in order to reach a compromise between simplicity and reliability of the formulation. Time-domain techniques can accurately model system nonlinearities and are mostly used for power quality problems such as transient and stability issues under nonsinusoidal operating conditions. They require more computation time than frequency-domain approaches but can accurately model nonlinearities (e.g., saturation and hysteresis), transients, and stability associated with transformers, nonlinear loads, and synchronous generators. Some techniques are based on a combination of frequency- and time-domain methods. In the frequency domain, the power system is linearly modeled while nonlinear simulation of components and loads can be accurately performed in the time domain. Hybrid time- and frequency-domain techniques result in moderate computational speed and accuracy.
This chapter starts with a review of power system matrices and the fundamental Newton–Raphson load flow algorithm. In Section 7.4, the Newton–Raphson harmonic power flow formulation is presented and explained in detail. In the last part of this chapter, a survey and classification of harmonic power flow approaches are addressed. All phasors are in per unit (pu) and all phase angles are assumed to be in radians.
7.1 Overview of a modern power system
The power system of today is a complicated interconnected network consisting of the following major sections as is illustrated in Fig. 7.1:

• transmission and subtransmission,
• distribution, and
• linear and nonlinear loads.
Generation
The three-phase AC synchronous generator or alternator is one of the fundamental components of a power system consisting of two synchronously rotating fields: one field is produced by the rotor driven at synchronous speed and excited by DC current. The DC current in the rotor winding is provided by an excitation system with or without slip rings. The second field is set up through the stator windings by the three-phase armature currents.
An important element of power systems are AC generators with rotating rectifiers, known as brushless excitation systems [1]. The excitation system controls the generator voltage and indirectly controls the reactive power flow within the power system together with synchronous condensers and capacitor banks. The slip ring free rotor enables the generation of high power – from 50 MVA up to 1600 MVA – at high voltages, typically in the 30–40 kV range. Hydrogen and water cooling permit the high power density of synchronous generators, which are mostly of the 2 and 4-pole types. Hydrogenerators are of the synchronous and of the induction machine types and can have up to 40 poles [2]. The source of mechanical power for AC generators may be water turbines, steam turbines (where the steam is either generated by coal, natural gas, oil, or nuclear fuel), and gas turbines for peak-power generation. Coal or natural gas fired plants have an efficiency of about 30% [3], whereas combined-cycle plants (gas turbine in series with a steam turbine) can reach efficiencies of about 60% [4]. Today’s deregulated power system also relies on distributed renewable energy resources such as solar, fuel cells, and turbines driven by wind, tides, water, and biomass generated gas. In a typical power station several generators are connected to a common point called a bus and operated in parallel to provide the total required power.
Transformers
Another key component of a power system is the transformer. Its role is to transform power with very high efficiency (e.g., 98%) from one level of voltage to another. Using a step-up transformer of turns ratio a will reduce the secondary current by a ratio of 1/a. This will reduce the real power loss I2R and the reactive power I2X of the transmission line, which makes the transmission of power over long distances feasible.
Due to insulation requirements and other practical design problems, terminal voltages of generators are limited to relatively low values, typically in the 30–40 kV range. Consequently, step-up transformers are used for transmission of power. At the receiving end of a transmission line, step-down transformers are employed to reduce the voltage to suitable levels for distribution or direct utilization. The power may go through several transformers between generator and the end user.
Transmission and Subtransmission
Overhead transmission lines permit the transfer of energy from generating units to the distribution system that serves the end users. Transmission lines also interconnect neighboring utilities to permit economic dispatch of power within regions during normal operating conditions, as well as transfer of power between regions during emergencies. Transmission-line voltage levels above 60 kV are standardized at 69 kV, 115 kV, 138 kV, 161 kV, 230 kV, 345 kV, 500 kV, and 745 kV. Transmission voltages above 230 kV are referred to as extrahigh voltage (EHV). High-voltage transmission lines are terminated at substations.
There are three types of substations: high-voltage substations, receiving substations, and primary substations. At the primary substations, the voltage is stepped down through a transformer to a value suitable for end users. For example, large industrial customers may be served directly from the transmission system.
The segment of the transmission system that connects high-voltage substations through step-down transformers to distribution substations is called the subtransmission network. There is no clear delineation between transmission and subtransmission voltage levels. Typically, the subtransmission voltage levels range from 69 kV to 138 kV. Some large industrial customers may be served from the subtransmission system. Capacitor and reactor banks are usually installed in subtransmission substations for maintaining or controlling the transmission line voltage. It is well known that for distribution voltages higher than 15 kV ferroresonance may occur if cables instead of overhead lines are used. To avoid this problem, gas-insulated underground cables are relied on to deliver in cities the power at high voltages.
Distribution
The distribution system (in the range of 4 kV to 34.5 kV) connects distribution substations to end users. Some small industrial consumers may be served directly by primary feeders. The secondary distribution network reduces the voltage for utilization by commercial and residential consumers. Either overhead transmission lines or cables are employed to deliver power to consumers. Typical secondary distribution systems operate at levels of 240/120 V (single-phase, three-wire), 208Y/120 V (three phase, four wire), and 480Y/277 V (three-phase, four-wire). The power for residential loads in the United States are derived from transformers that reduce the primary feeder voltage to 240/120 V using a single-phase, three-wire line. Distribution systems are made up of both overhead and underground lines. The growth of underground distribution has been extremely rapid, especially in new residential areas.
Linear and Nonlinear Loads
Power systems serve linear and nonlinear loads. Loads are divided into three key categories within a power system: industrial, commercial, and residential. Industrial loads are functions of both voltage and frequency. Induction motors form a high proportion (e.g., 60%) of these loads. Commercial and residential loads consist largely of lighting, heating, and cooling (e.g., induction motors). These loads are largely independent of frequency and consume reactive power with a total power factor of larger than TPF = 80%.
The nonlinear (v–i) characteristics of nonlinear loads generate both current and voltage harmonics and call for nonsinusoidal analysis and modeling of power systems. A typical power system consists of a few large industrial nonlinear loads (e.g., large rectifier bridges, large variable-speed drives); however, the number of small nonlinear loads (such as power electronic rectifiers, high-efficiency lighting, and small variable-speed drives) is rapidly increasing. This requires attention to such nonlinear loads during the design, planning, and operation of distribution systems.
7.2 Power system matrices
Frequency- and time-domain techniques employ vectors and matrices for mathematical modeling of power systems and for defining input and output variables. This section deals with the bus admittance and the Jacobian matrices, which are essential components of all power flow formulations.
7.2.1 Bus Admittance Matrix
Table 7.1 presents a review of circuit-component definitions and laws. Ohm’s and Kirchhoff’s laws can be used for matrix formulations that are useful for load flow analyses. This approach yields two matrices:
Table 7.1
Review of Circuit Definitions and Laws
| Circuit-component definitions | Circuit laws | ||
| Resistance Conductance | R G = 1/R | Ohm’s law | V = IZ V = I/Y |
| Inductance Reactance (inductive) | L jωL | Kirchhoff’s voltage-loop law (KVL) | ΣV = 0, leads to loop matrix |
| Capacitance Reactance (capacitive) | C 1/jωC = –j/ωC | Kirchhoff’s current-node law (KCL) | ΣI = 0, leads to bus matrix |
| Impedance | Z = R + jωL (e.g., inductor) | ||
| Z = R – j/ωC (e.g., capacitor) | |||
| Admittance | Y = 1/Z | ||
| Susceptance | B = 1/X |

• Kirchhoff’s current law (KCL) generates bus matrices, which result from the fact that the sum of currents entering a bus is zero.
• Kirchhoff’s voltage law (KVL) results in loop matrices, which describe voltages in a circuit loop.
The bus matrix written in terms of admittance originates directly from the KCL applied to each circuit bus other than the reference (ground) bus.
7.2.1.1 Application Example 7.1: A Simple Power System Configuration
Draw the single-phase representation of a simple power system with bus 1 (called the swing bus) connected to buses 2 and 4 (through a transmission line), bus 2 connected to bus 3, and bus 3 connected to the reference ground (bus 0).
Solution to Application Example 7.1
The single-phase representation of the power system is shown in Fig. E7.1.1.

Let j be an arbitrary circuit bus other than the reference bus (which is denoted as bus 0), as shown in Fig. 7.2. Then
n∑i=1˜Iji=˜Ij,
where ˜Iji≡line![]() line current, which leaves bus j and enters bus i via a line and ˜Ij≡current
line current, which leaves bus j and enters bus i via a line and ˜Ij≡current![]() current injected at bus j from an external source or bus injection current. The tilde (~) above Ĩji and Ĩj denotes a complex line current and a complex bus injection current, respectively.
current injected at bus j from an external source or bus injection current. The tilde (~) above Ĩji and Ĩj denotes a complex line current and a complex bus injection current, respectively.

Application of Ohm’s law (Fig. 7.3) leads to
˜Iji=˜yji(˜Vj−˜Vi),
where ỹji is the complex line admittance of a line from bus j to bus i.

Certain elements of n∑i=1˜Iji=˜Ij![]() are zero:
are zero:
• The current Ĩjj is zero since no line joins bus j with bus j and this is reflected in ˜Ijj=˜yjj(˜Vj−˜Vj)![]() because it gives zero for Ĩjj due to (˜Vj−˜Vj)=0;
because it gives zero for Ĩjj due to (˜Vj−˜Vj)=0;![]() and
and
• Ĩji will be zero if no line exists between j and i, the “line impedance” is infinite, and the “line admittance” ỹji is zero. One can write now (introducing Eq. 7-2 into Eq. 7-1)
n∑i=1˜yji(˜Vj−˜Vi)=˜Ij.
Note that ˜Vj![]() and ˜Vi
and ˜Vi![]() are bus voltages with respect to bus 0, the reference (ground) bus. Equation 7-3 is written for i = 1, 2, …, n and the coefficient of voltage ˜Vj
are bus voltages with respect to bus 0, the reference (ground) bus. Equation 7-3 is written for i = 1, 2, …, n and the coefficient of voltage ˜Vj![]() in the Kirchhoff equation at bus j is n∑i=1˜yji
in the Kirchhoff equation at bus j is n∑i=1˜yji![]() whereas the coefficient of ˜Vi(i≠j)
whereas the coefficient of ˜Vi(i≠j)![]() in the jth equation is (−˜yji).
in the jth equation is (−˜yji).![]()
All equations now read (n × n equation system) as follows,
for j = 1:
˜I1=(n∑i=1i≠1˜y1i)˜V1+(−˜y12)˜V2+…+(−˜y1n)˜Vn,
for j = 2:
˜I2=(−˜y21)˜V1+(n∑i=1i≠2˜y2i)˜V2+…+(−˜y2n)˜Vn,
for j = n:
˜In=(−˜yn1)˜V1+(−˜yn2)˜V2+…+(n∑i=1i≠n˜yni)˜Vn.
Observe the pattern of the coefficients of the bus voltages on the right-hand side of the equation system. This pattern will be generalized as the rule for the formation of a matrix of coefficients of ˜Vj![]() . The above n equations can be written in matrix form
. The above n equations can be written in matrix form
ˉIbus=ˉYbusˉVbus,
where Ībus is the bus injection vector representing the n phasor injection currents, ˉYbus![]() is the bus admittance matrix (it is an n × n matrix of coefficients formed as indicated above), and ˉVbus
is the bus admittance matrix (it is an n × n matrix of coefficients formed as indicated above), and ˉVbus![]() is the bus voltage vector of n phasor voltages referenced to bus 0:
is the bus voltage vector of n phasor voltages referenced to bus 0:
˜Vn=˜Φn−˜Φ0=˜Φn,
where ˜Φn![]() and ˜Φ0
and ˜Φ0![]() are the potentials at bus n and bus 0, respectively, and ˜Φ0
are the potentials at bus n and bus 0, respectively, and ˜Φ0![]() = 0.
= 0.
If ˉYbus![]() is a nonsingular matrix then its inverse (ˉYbus)−1
is a nonsingular matrix then its inverse (ˉYbus)−1![]() can be found and there exists a solution to the matrix equation. If ˉYbus
can be found and there exists a solution to the matrix equation. If ˉYbus![]() is singular then (ˉYbus)−1
is singular then (ˉYbus)−1![]() cannot be found and there exists no solution to the matrix equation.
cannot be found and there exists no solution to the matrix equation.
ˉIbus=ˉYbusˉVbus.↑↑↑n×1n×nn×1︸↑↑n×1rowcolumn
Note that the injection currents find a return path through bus 0 (ground). Also note that the Kirchhoff current law is not applied to bus 0 in these equations; however, the total current entering bus 0 is the negative sum of the currents Ĩ1, Ĩ2, … Ĩn. Therefore, the Kirchhoff current law at bus 0 is
−∑ni=1˜Ij=−[(−˜y21−˜y31−…−˜yn1+n∑i=1i≠1˜y1i)˜V1+(−˜y12−˜y32−…−˜yn2+n∑i=1i≠2˜y2i)˜V2+…],
which can be readily simplified as
˜I0=−˜y01˜V1−˜y02˜V2−…−˜y0n˜Vn,
where ỹ0k is the primitive admittance joining buses 0 and k.
Because the relation in Eq. 7-9 is a linear combination of the previous n equations, it cannot be used to obtain additional information beyond that given in the n × n equation system. Inspection of the coefficients of the ˜V![]() terms in the n × n equation system reveals a rule for the formation of ˉYbus
terms in the n × n equation system reveals a rule for the formation of ˉYbus![]() . The following rules are used to “build” the bus admittance matrix referenced to bus 0.
. The following rules are used to “build” the bus admittance matrix referenced to bus 0.
The Admittance Matrix Building Algorithm
• yjj: the diagonal entries of ˉYbus![]() are formed by summing the admittances of lines terminating at bus j. Note there is no tilde on yjj.
are formed by summing the admittances of lines terminating at bus j. Note there is no tilde on yjj.
• yij: the off-diagonal entries are the negatives of the admittances of lines between buses i and j. If there is no line between i and j, this term is zero. Note there is no tilde on yij.
Usually, bus 0 is the ground bus, but other buses may be chosen as the reference (for specialized applications). Since bus 0 is commonly chosen as the reference, the notation
ˉYbus=ˉY(0)bus
is employed to denote the bus admittance matrix referenced to ground. If some other bus is used as the reference, for example bus k, the following notation is used:
ˉY(k)bus.
7.2.1.2 Application Example 7.2: Construction of Bus Admittance Matrix
Construct the bus admittance matrix for the simple 4 bus power system of Fig. E7.2.1.

Solution to Application Example 7.2
The ˉYbus![]() admittance matrix is for Figure E7.2.1
admittance matrix is for Figure E7.2.1
[ˉYbus]=[y11y12y13y14y21y22y23y24y31y32y33y34y41y42y43y44]
where the entries yij of Eq. E7.2-1 are as a function of the admittances ỹij for i = 1…4 and j = 1…4:
y11= ỹ12+ ỹ14, y12=-ỹ12, y13= 0, y14=-ỹ14,
y21=-ỹ12, y22= ỹ12+ ỹ23, y23=-ỹ23, y24= 0,
y31= 0, y32=-ỹ23, y33= ỹ23+ ỹ30, y34= 0,
y41=-ỹ14, y42= 0, y43= 0, y44= ỹ14, and
−4∑j=1˜Ij=−(˜I1+˜I2+˜I3+˜I4)=˜I0.
Inspection of the ˉYbus![]() building algorithm reveals several properties of the bus matrix:
building algorithm reveals several properties of the bus matrix:
• ˉYbus![]() is complex and symmetric;
is complex and symmetric;
• ˉYbus![]() is sparse since each bus is connected to only a few nearby buses, and this causes many yji = 0 entries; and
is sparse since each bus is connected to only a few nearby buses, and this causes many yji = 0 entries; and
• Provided that there is a net nonzero admittance tie to the reference bus (e.g., ground), ˉYbus![]() is nonsingular and may be inverted to find ˉVbus
is nonsingular and may be inverted to find ˉVbus![]() from
from
ˉIbus=ˉYbusˉVbus,
or
ˉVbus=(ˉYbus)−1ˉIbus.
If there are no ties to the reference bus, ˉYbus![]() is singular and cannot be inverted because no solution to the n × n equation system exists.
is singular and cannot be inverted because no solution to the n × n equation system exists.
7.2.1.3 Application Example 7.3: Building of Nonsingular Bus Admittance Matrix
Construct the bus abmittance matrix for the 3 bus power system of Fig. E7.3.1.

Solution to Application Example 7.3
Note: Off-diagonal entries = sum of negatives of the line admittances
y21=y12=–(1+j)1/Ω,y31=y13=–(1+j)1/Ω,y32=y23=–(1+j)1/Ω,Main−diagonalentryforbus1:y11=(2+2j)1/Ω,Maindiagonalentryforbus2:y22=(2+2j)1/Ω,Main−diagonalentryforbus3:y33=(3+3j)1/Ω,
Therefore,
ˉYbus=[y11y12y13y21y22y23y31y32y33]=[(2+2j)−(1+j)−(1+j)−(1+j)(2+2j)−(1+j)−(1+j)−(1+j)(3+3j)].
ˉYbus![]() is complex and symmetric, but not sparse.
is complex and symmetric, but not sparse.
7.2.1.4 Application Example 7.4: Building of Singular Bus Admittance Matrix
Construct the bus abmittance matrix for the simple 4 bus power system of Fig. E7.4.1.

Solution to Application Example 7.4
ˉIbus=ˉYbusˉVbus=[(2+2j)−(1+j)−(1+j)−(1+j)(2+2j)−(1+j)−(1+j)−(1+j)(2+2j)][˜V1˜V2˜V3],
˜I1=(2+2j)˜V1−(1+j)˜V2−(1+j)˜V3
˜I2=−(1+j)˜V1+(2+2j)˜V2−(1+j)˜V3
˜I3=−(1+j)˜V1−(1+j)˜V2+(2+2j)˜V3
(˜I1+˜I2)=(1+j)˜V1+(1+j)˜V2−(2+2j)˜V3
or
(˜I1+˜I2)︸I3=−(1+j)˜V1−(1+j)˜V2+(2+2j)˜V3
Note that Eq. E7.4-2 + Eq. E7.4-3 = Eq. E7.4-5, which is the same as Eq. E7.4-4. That is, these equations are dependent. One concludes that the matrix is singular and no solution exists for Eqs. E7.4-2 to E7.4-4.
7.2.2 Triangular Factorization
In the United States there exist three power grids: the Eastern, Western, and Texan power systems. Because of stability problems these grids are linked with small (100 MW range) DC tie lines. Nevertheless if even one of the grids is analyzed, the number of buses will be very large: a few thousand buses or more, depending on the detail of modeling. Fortunately, not all buses are mutually linked through a transmission line and for this reason the resulting bus admittance matrix is very sparse, that is, only about 1% of the entire matrix entries are nonzero. However, because of the large dimensions (few thousands) a direct solution (e.g., Gaussian elimination) of the equation system is not feasible and one uses the Newton–Raphson method together with the Jacobian matrix to arrive at the solution via iterations.
To reduce computer memory requirements, sparsity programming is used: it is a digital programming technique whereby sparse matrices are stored in compact forms. The usual basis of sparsity programming techniques is the storage of only nonzero entries. Two broad classes of sparsity programming techniques are
• the entry-row-column storage method, and
• the chained-data-structure method.
Applications of sparsity programming methods are primarily in ˉYbus![]() methods. In this chapter the Jacobian will be used; this matrix is as sparse as the ˉYbus
methods. In this chapter the Jacobian will be used; this matrix is as sparse as the ˉYbus![]() matrix and lends itself to sparsity programming.
matrix and lends itself to sparsity programming.
In power engineering, as well as in many other branches of engineering, it is necessary to solve a simultaneous set of algebraic linear equations. The general form is the solution of
ˉA⋅ˉx=ˉb
Given are the n by n matrix Ā and the n-dimensional vector ˉb![]() . Such is the case in the solution of
. Such is the case in the solution of
ˉIbus=ˉYbusˉVbus
or
ˉVbus=[ˉYbus]−1ˉIbus
for ˉVbus![]() where the injection currents and the admittance matrix are given. Using the notation of ˉA⋅ˉx=ˉb
where the injection currents and the admittance matrix are given. Using the notation of ˉA⋅ˉx=ˉb![]() , let Ā be factored into two matrices called triangular factorization:
, let Ā be factored into two matrices called triangular factorization:
ˉA=ˉL⋅ˉU
where ˉL![]() is lower left triangular (e.g., lrc is zero for c > r) and Ū is upper right triangular (e.g., urc is zero for r > c). Then
is lower left triangular (e.g., lrc is zero for c > r) and Ū is upper right triangular (e.g., urc is zero for r > c). Then
ˉA⋅ˉx=[ˉL⋅ˉU]ˉx=ˉb
Let (ˉU⋅ˉx)![]() be a new variable ˉw
be a new variable ˉw![]() , which is an n-dimensional vector; then
, which is an n-dimensional vector; then
ˉw=ˉU⋅ˉx
ˉL⋅ˉw=ˉb
where
ˉw=[w1w2⋮wn],ˉb=[b1b2⋮bn],
ˉL=[l1100.l21l22..l31l32l33.....],ˉU=[u11u12u13.0u22u23.00u33.....].
Note that ˉx![]() and ˉb
and ˉb![]() correspond to the ˉVbus
correspond to the ˉVbus![]() vector and the current vector Ībus, respectively.
vector and the current vector Ībus, respectively.
7.2.2.1 Application Example 7.5: Matrix Multiplication
Given
ˉU=[u11u120u22],ˉL=[l110l21l22].
Find entries of the matrix ˉL![]() · Ū.
· Ū.
Solution to Application Example 7.5
ˉL⋅ˉU=[l110l21l22]⋅[u11u120u22]=[(l11u11)(l11u12)(l21u11)(l21u12+l22u22)]
7.2.2.2 Application Example 7.6: Triangular Factorization
Given
ˉU=[u11u120u22],ˉx=[x1x2],
show that ˉw![]() = Ū · ˉx
= Ū · ˉx![]() is a column (n = 2) vector.
is a column (n = 2) vector.
Solution to Application Example 7.6
ˉw=ˉU⋅ˉx=[u11u120u22]︸2×2[x1x2]︸2×1↑↑↑↑rowcolumnrowcolumn
ˉw=[u11x1+u12x2u22x2].
Therefore, ˉw![]() is a 2 × 1 matrix or a column vector.
is a 2 × 1 matrix or a column vector.
Forward Substitution
ˉL![]() · ˉw
· ˉw![]() = ˉb
= ˉb![]() is readily solved for ˉw
is readily solved for ˉw![]() since the form of the equation is rather special:
since the form of the equation is rather special:
ˉL=[l11000.l21l2200.l31l32l330......][w1w2⋮wn]=[b1b2⋮bn].
The top row of the matrix equation is solved readily for w1 since the only nonzero entry on the left-hand side is l11w1 and therefore
l11w1=b1,
or
w1=b1l11.
From row 2 one finds
l21w1+l22w2=b2,
or
w2=b2−l21w1l22.
This process of forward substitution continues until all components of ˉw![]() are computed.
are computed.
Having found vector ˉw![]() , the relation ˉw
, the relation ˉw![]() = Ū · ˉx
= Ū · ˉx![]() is used to find ˉx
is used to find ˉx![]() :
:
[w1w2⋮wn]=[u11u12u13.0u22u23.00u33.....][x1x2⋮xn].
Backward Substitution
The bottom row is readily solved (n = 3) for x3:
w3=u33x3,
or
x3=w3u33.
The second row from the bottom yields
w2=u22x2+u23x3
or
x2=w2−u23x3u22.
Rule: The value of xn is backward substituted into the (n – 1)st row of the above matrix equation to find xn-1 from
wn−1=un−1n−1xn−1+un−1nxn.
This process of back substitution is employed to find all other components of ˉx![]() .
.
Note: By the process of
(i) triangular factorization of Ā,
(ii) forward, and
(iii) backward substitution,
the solution of Ā · ˉx![]() = ˉb
= ˉb![]() is found without inverting Ā ! At first glance, it may appear remarkable that the inversion of Ā may be avoided, but there is some information that lies uncalculated in the use of triangular factorization compared to a solution using inversion. If Ā · ˉx
is found without inverting Ā ! At first glance, it may appear remarkable that the inversion of Ā may be avoided, but there is some information that lies uncalculated in the use of triangular factorization compared to a solution using inversion. If Ā · ˉx![]() = ˉb
= ˉb![]() is to be solved for many different values of ˉb
is to be solved for many different values of ˉb![]() , inversion is readily used since a given vector ˉb
, inversion is readily used since a given vector ˉb![]() premultiplied by ˉA−1
premultiplied by ˉA−1![]() gives the required result ˉx
gives the required result ˉx![]() = ˉA−1
= ˉA−1![]() · ˉb
· ˉb![]() . In such an application ˉA−1
. In such an application ˉA−1![]() is calculated only once.
is calculated only once.
If triangular factorization is used, the forward/backward substitution process would have to be repeated for each different ˉb![]() vector. In power engineering applications, however, it is usually necessary to solve Ā · ˉx
vector. In power engineering applications, however, it is usually necessary to solve Ā · ˉx![]() = ˉb
= ˉb![]() only once: the inverse of Ā is not really desired – only ˉx
only once: the inverse of Ā is not really desired – only ˉx![]() is sought. The triangular factorization method is favored for most applications.
is sought. The triangular factorization method is favored for most applications.
The success of the triangular factorization method depends on
• the speed of the factorization of Ā into ˉL![]() and Ū, and
and Ū, and
• the sparsity of ˉL![]() and Ū.
and Ū.
A sparse Ā is of considerable interest because if the triangular matrices were sparse, the memory advantages of sparsity programming may be added to the speed advantages of triangular factorization.
Formation of the Table of Factors
Let ˉL![]() have unit (main) diagonal entries
have unit (main) diagonal entries
ˉL=[100.l2110.l31l321.....],ˉU=[u11u12u13.0u22u23.00u33.....]
and let Ū be stored superimposed onto ˉL![]() (omitting the writing of the unit entries of ˉL
(omitting the writing of the unit entries of ˉL![]() ):
):
[u11u12u13.l21u22u23.l31l32u33.....].
This superimposed array is called the table of factors. The upper right triangle of the table is Ū; the lower left triangle is ˉL![]() with the unit diagonal entries deleted.
with the unit diagonal entries deleted.
7.2.3 Jacobian Matrix
The proposal to use for a partial derivative “∂![]() ” instead of “d” stems from Carl Gustav Jacob Jacobi, 1804–1851, a German mathematician. At about the same time as Jacobi, the Russian mathematician Michail Vasilevich Ostrogradski (1801–1862) also introduced the Jacobian of n functions y1, y2, …, yn and n unknowns x1, x2, …, xn as follows:
” instead of “d” stems from Carl Gustav Jacob Jacobi, 1804–1851, a German mathematician. At about the same time as Jacobi, the Russian mathematician Michail Vasilevich Ostrogradski (1801–1862) also introduced the Jacobian of n functions y1, y2, …, yn and n unknowns x1, x2, …, xn as follows:
ˉJ=[∂y1∂x1∂y1∂x2…∂y1∂xn∂y2∂x1∂y2∂x2…∂y2∂xn⋮⋮⋮⋮∂yn∂x1∂yn∂x2…∂yn∂xn].
It is possible to factorize arbitrary nonsingular matrices ˉJ![]() into ˉL
into ˉL![]() and Ū without the need for new computer storage areas: in other words, ˉJ
and Ū without the need for new computer storage areas: in other words, ˉJ![]() is destroyed and replaced by the table of factors. The table of factors is approximately as sparse as ˉJ
is destroyed and replaced by the table of factors. The table of factors is approximately as sparse as ˉJ![]() and, therefore, the table of factors does not require additional storage.
and, therefore, the table of factors does not require additional storage.
Techniques that result in the destruction of the original data and the replacement of those data by the solution are known as in situ methods. Matrix ˉJ![]() is factored into ˉL
is factored into ˉL![]() and Ū in situ and ˉJ
and Ū in situ and ˉJ![]() is destroyed and replaced by the table of factors.
is destroyed and replaced by the table of factors.
The formulas required for the calculation of the table of factors are readily found, noting that
ˉL⋅ˉU=ˉJ(=ˉA)
Write ˉL![]() and Ū, and find the entries of ˉL
and Ū, and find the entries of ˉL![]() and Ū, that is, the table of factors:
and Ū, that is, the table of factors:
[1000.l21100.l31l3210......][u11u12u13.0u22u23.00u23.....]=ˉJ=[J11J12J13.J21J22J23.J31J32J33.....].
7.2.3.1 Application Example 7.7: Jacobian Matrices
Given
[10l211][u11u120u22]=[J11J12J21J22].
Find u11, u12, u22, and l21.
Solution to Application Example 7.7
J11=u11oru11=J11J12=u12oru12=J12J21=l21u11orl21=J21/u11J22=l21u12+u22oru22=J22−l21u12
In general,
u11=J11u12=J12⋮⋮u1c=J1c⋮⋮u1n=J1n
Since the first row of the table of factors is row 1 of Ū, the first row of the table of factors is simply row 1 of ˉJ![]() .
.
In row 2 of ˉJ![]() :
:
l21u11=J21l21u12+u22=J22l21u13+u23=J23.......
These equations yield l21, u22, u23, u24, …
l21=J21/u11u22=J22−l21u12u23=J23−l21u13.......
Thus in the expansion of row 2 of ˉJ![]() , one l and (n – 1) u’s are formed. The generalization for the expansion of row r of ˉJ
, one l and (n – 1) u’s are formed. The generalization for the expansion of row r of ˉJ![]() is straightforward:
is straightforward:
lrc=Jrc−c−1∑q=1lrquqcucc,forc=1,2,…,(r−1)
urc=Jrc−r−1∑q=1lrquqc,forc=r,r+1,…,n.
The rules for the formation of the table of factors in situ are as follows:
1) Row 1 of ˉJ![]() is not modified.
is not modified.
2) Row 2 of ˉJ![]() is modified to yield one l and (n – 1) u’s. These entries are found using the above two equations for lrc and urc. For these equations, when the summation upper index is zero, there are no terms in the sum (e.g., ignore the summation term). When the upper and lower indices of summation are the same, there is a single term in the sum.
is modified to yield one l and (n – 1) u’s. These entries are found using the above two equations for lrc and urc. For these equations, when the summation upper index is zero, there are no terms in the sum (e.g., ignore the summation term). When the upper and lower indices of summation are the same, there is a single term in the sum.
3) Rule 2 is repeated for each row and ˉJ![]() is replaced by the table of factors. In row r, there will be (r – 1) l-terms calculated and (n – r + 1) u-terms. The above equations for lrc and urc are used.
is replaced by the table of factors. In row r, there will be (r – 1) l-terms calculated and (n – r + 1) u-terms. The above equations for lrc and urc are used.
Forward and Backward Substitutions
The solution of a simultaneous set of algebraic linear equations by triangular factorization involves two main steps:
• formation of the table of factors, and
• forward/backward substitutions.
Having found the table of factors as indicated previously, the following relations are used to complete the solution:
ˉL⋅ˉw=ˉbˉU⋅ˉx=ˉw.
Vector ˉb![]() is destroyed in this process and converted in situ to vector ˉw
is destroyed in this process and converted in situ to vector ˉw![]() . Since l11 is unity, w1 is simply b1 as can be seen from the matrix solution
. Since l11 is unity, w1 is simply b1 as can be seen from the matrix solution
[l11000.l21l2200.l31l32l330......][w1w2⋮wn]=[b1b2⋮bn].
Subsequent rows of ˉw![]() are found using
are found using
wr↑created=br↑destroyed−forr=1,2,3,4,5,6,....,nr−1∑q=1lrqwq.
As this equation is used, w1 replaces b1, w2 replaces b2, and so on.
Having found w1 a similar process is used to find ˉx![]() :
:
[u11u12u13.0u22u23.00u33.....][x1x2⋮xn]=[w1w2⋮wn].
By inspection,
unnxn=wn
or
xn=wnunn.
Again, in situ technique is used and xn replaces wn.
In row n – 1:
un−1n−1xn−1+un−1nxn=wn−1
or
xn−1=wn−1−un−1nxnun−1n−1.
Element xn–1 replaces wn–1. The process continues for rows n – 2, n – 3, …, 1. In row r
xr=wr−n∑q=r+1urqxqurr.
This completes the solution.
7.3 Fundamental power flow
The electric power flow problem is the most studied and documented problem in power engineering. It is the calculation of line loading given the generation and demand levels of P, Q, and S measured in kW, kVAr, kVA, respectively. The transmission network is (nearly) linear, and one might expect the power flow to be a linear problem. However, because power p = (v · i) is a product of voltage v and current i, the problem formulation is nonlinear even for a linear transmission network. Additional nonlinearities arise from the specification and use of complex voltages and currents. Also, there are transmission component nonlinearities that may be considered, such as tap changing transformers, in which the tap is adjusted to hold a given bus voltage at a fixed magnitude.
The power flow formulation does not consider time variations of loads, generation, or network configuration. The sinusoidal steady state is assumed and, as a result, equations are algebraic in form rather than differential.
Prior to 1940 there were a limited number of interconnected power systems and the servicing of the load was elementary since the systems were primarily radial circuits (Fig. 7.4). In more recent years, the numerous advantages of interconnection were recognized, and modern power systems are characterized by a high degree of interconnection (Fig. 7.5), for example, within the three U.S. power grids (Western, Eastern, and Texan power systems). Many loop circuits with many load/generation buses and high levels of power exchange between neighboring companies exist. The latter point relates closely to interconnection advantages.


With no addition of generation capacity, it is possible to increase the generation available through interconnection. For example, in the case of an outage of a generating unit, power may be purchased from a neighboring company. The cost savings realized from lower installed capacity usually far outweigh the cost of the transmission circuits required to access neighboring companies. The analysis of large interconnected power systems generally involves the simultaneous solution of many (thousands) nonlinear algebraic equations using the Newton–Raphson approach. Like most engineering problems, the power flow problem has a set of given data and a set of quantities that must be calculated.
In this section, each complex unknown will be counted as two real unknowns, and each complex equation will be considered as two real equations. The objective of fundamental power flow is to calculate line loading for given generation and load levels (P, Q, and S).
7.3.1 Fundamental Bus Admittance Matrix
As discussed and formulated in the previous section, for an n bus system (not including the ground bus, which is the reference bus), the fundamental bus admittance matrix is an n × n matrix:
ˉYbus=[y11y12…y1ny21y22…y2n⋮⋮⋮⋮yn1yn2…ynn],
where f1 = 60 Hz and ω1 = 2πf1 = 377 rad/s.
The entries of ˉYbus![]() are found as follows:
are found as follows:
ykk = sum of line admittances connected to bus k (k = 1, 2, …, n).
Off-diagonal entries:
ykj = –(line admittance connected between buses k and j).
Since ykj = yjk, the matrix ˉYbus![]() is symmetric.
is symmetric.
7.3.2 Newton–Raphson Power Flow Formulation
The power (load) flow problem consists of calculations of power flows (real, reactive) and voltages (magnitude, phase) of a network for specified (demand and generation powers) terminal or bus conditions. All voltages and currents are assumed to have fundamental (h = 1, f1 = 60 Hz) frequency components. A single-phase representation is considered to be adequate because power systems are approximately balanced within all three phases. Associated with each bus (e.g., bus j) are four quantities:
• reactive power Q,
• root-mean-squared (rms) voltage value |˜V|![]() , and
, and
• phase angle of voltage δ.
Three types of buses are represented and two of the four quantities are specified at each bus:
• Swing bus. It is necessary to select one reference bus (called the swing or slack bus) providing the transmission losses because these are unknown until the final solution is available. The voltage amplitude and its phase angle are given at the swing bus (usually 1.0 per unit (pu) and zero radians, respectively), and all other bus voltage angles are measured with respect to the phase angle of this reference bus. The remaining buses are either PV or PQ buses.
• Voltage controlled (PV) buses. The real power P and the voltage magnitude (amplitude) |˜V|![]() are specified for PV buses. These are usually the generation buses at which the injected real power is specified and held fixed by turbine settings (e.g., steam entry valve). A voltage regulator holds |˜V|
are specified for PV buses. These are usually the generation buses at which the injected real power is specified and held fixed by turbine settings (e.g., steam entry valve). A voltage regulator holds |˜V|![]() fixed at PV buses by automatically varying the generator field excitation.
fixed at PV buses by automatically varying the generator field excitation.
• Load (PQ) buses. These are mostly system loads at which real and reactive powers (P and Q, respectively) are specified.
The following notations will be used:
• For a given bus (e.g., the jth bus):
• Qj = reactive power
• |˜Vj|![]() = rms value of voltage, and
= rms value of voltage, and
• δj = angle of voltage.
• For the swing or slack bus (j = 1):
• δ1 = 0 radians, and
• It will cover all transmission line losses of the system (“slack”).
• For a PV bus (e.g., the jth bus):
• Pj is given by turbine setting, and
• |˜Vj|![]() is given by generator excitation.
is given by generator excitation.
• For a PQ bus (e.g., the jth bus):
• Pj and Qj are given by the load demand,
• because power values are given (p = v · i) one obtains an algebraic, nonlinear system of equations.
Fundamental Bus Voltage Vector
For power system modeling at rated frequency, the bus voltage vector is defined as (note: the bar above the x means vector, and t means transpose):
ˉx=[δ2,|˜V2|,δ3,|˜V3|,…δn,|˜Vn|]t
where δj is the phase shift of voltage at bus j with respect to the swing bus voltage phase angle and |˜Vj|![]() is the voltage rms magnitude at bus j. Note that if bus 1 is the swing bus, |˜V1|
is the voltage rms magnitude at bus j. Note that if bus 1 is the swing bus, |˜V1|![]() and δ1 are known (usually 1.0 per unit and zero radians).
and δ1 are known (usually 1.0 per unit and zero radians).
Although power system components are assumed to be linear in the conventional power flow formulation, the problem is a nonlinear one because power p is the product of voltage v and current i. The load flow problem requires the solution of algebraic but nonlinear equations, which are solved using the Newton–Raphson method as will be discussed next.
i) Linear approximation, one-dimensional analysis (Fig. 7.6):
F(x1)=(x1−x0)dF(x0)dx,
where h = (x1 – x0), or
F(x1)=hdF(x0)dx,
[dF(x0)dx]−1F(x1)=(x1−x0),
x1=x0+[dF(x0)dx]−1F(x1),
or
x1↑updatedguessafterfirstiteration=x0↑firstguess+F(x1)[dF(x0)dx].

ii) Taylor series for one variable (Fig. 7.7):
F(x)=F(x0)+(x−x0)1!F′(x0)+(x−x0)22!F″(x0)+…+(x−x0)nn!F(n)(x0)+…,
or
F(x0+h)=F(x0)+h1!F′(x0)+h22!F″(x0)+…+hnn!F(n)(x0)+…,
F(x0+h)≈F(x0)+h1!F′(x0)
F(x1)≈F(x0)+(x1−x0)F′(x0)
forF(x1)=0x1=x0−F(x0)F′(x0).

iii) Taylor series for two variables (replace “d” by “∂![]() ”, Fig. 7.6):
”, Fig. 7.6):
F(x0+h,y0+k)=F(x0,y0)+{∂F(x0,y0)∂xh+∂F(x0,y0)∂yk}+12{∂2F(x0,y0)∂x2h2+2∂2F(x0,y0)∂x∂yhk+∂2F(x0,y0)∂y2k2}+16{…}+…+1h!{…}+Rn,
where Rn is the remainder.
Equation 7-50 can be written in matrix form neglecting higher order terms:
F(x0+h,y0+k)=F(x0,y0)+[∂F(x0,y0)∂x∂F(x0,y0)∂y][kk],
where
h=(x1−x0)andk=(y1−y0)
or, for F(x1, y1) = 0,
[x1y1]=[x0y0]−F(x0,y0)[∂F(x0,y0)∂x∂F(x0,y0)∂y],
or
[x1y1]=[x0y0]−[∂F(x0,y0)∂x∂F(x0,y0)∂y]−1F(x0,y0).
Therefore,
[x1y1]=[x0y0]−(ˉJ)−1F(x0,y0),
where the two-dimensional Jacobian ˉJ![]() is
is
ˉJ=[∂F(x0,y0)∂x∂F(x0,y0)∂y].
Residuals of an Equation System
Given the equation system:
x1−2x2−4x3=03x1+x2+7x3=0.7x1−x2+x3=0
The approximate (guessed) solutions are x10, x20, x30. Introducing approximate solutions in the equation system:
x10–2x20–4x30=residual1
3x10+x20+7x30=residual2
7x10–x20+x30=residual3
If 3∑i=1|residuali|=0 , then solution of the equation system has been obtained.
, then solution of the equation system has been obtained.
Fundamental Mismatch Power
The power flow algorithm is based on the Newton–Raphson approach forcing the mismatch powers (at system buses) to zero. The mismatch powers (real and reactive powers) correspond to the residuals of the equation system as discussed above. Specifically the term “mismatch power” at bus i refers to the summation of the complex powers leaving via lines connected to bus i and the specified complex load (demand) power at this bus. Note that the bus itself cannot produce or dissipate power and therefore the mismatch power for a given bus must be zero. Therefore, the mismatch power vector is
ΔˉW=[P2+Fr,2,Q2+Fi,2,…Pn+Fr,n,Qn+Fi,n]t,
where Pj and Qj are the real and reactive load powers at bus j, respectively, and Fr,j and Fi,j are the real and reactive line powers computed later in this section. Figure 7.8 illustrates the definition of power at a given bus. Note the following:
• P2 > 0 demand (load) of real power,
• P2 < 0 generation of real power,
• Q2 > 0 demand (inductive load) of reactive power, and
• Q2 < 0 generation (capacitive load) of reactive power.

For an n-bus system consisting of the swing bus and PQ buses (inclusion of PV buses is considered later), the mismatch power vector has 2(n – 1) rows corresponding to buses 2 through n (bus 1 is assumed to be the swing bus). Clearly ΔˉW![]() is a function of ˉx
is a function of ˉx![]() , the bus voltage vector (Eq. 7-42).
, the bus voltage vector (Eq. 7-42).
The Fundamental Newton–Raphson Power Flow Algorithm
The power flow problem simplifies to finding ˉx![]() such that
such that
ΔˉW(ˉx)=0.
Let ˉxs![]() be the bus solution vector and expand Eq. 7-57 in a Taylor series about ˉx
be the bus solution vector and expand Eq. 7-57 in a Taylor series about ˉx![]() = ˉxs
= ˉxs![]() where ˉxs
where ˉxs![]() is the (guessed) solution (see Eqs. 7-46 and 7-52):
is the (guessed) solution (see Eqs. 7-46 and 7-52):
ΔˉW(ˉx)=ΔˉW(ˉxs)+ˉJ(ˉx−ˉxs),
or
ˉJ−1ΔˉW(ˉx)=ˉJ−1ΔˉW(ˉxs)+(ˉx−ˉxs),
where ˉJ![]() is the Jacobian.
is the Jacobian.
With ΔˉW(ˉx)![]() = 0 because ˉx
= 0 because ˉx![]() is the (converged) solution vector,
is the (converged) solution vector,
ˉx=ˉxs−ˉJ−1ΔˉW(ˉxs).
Due to the linearization (neglect of higher order terms), the solution ˉxs![]() of Eq. 7-60 is an approximation which only can be improved by iterations. Therefore,
of Eq. 7-60 is an approximation which only can be improved by iterations. Therefore,
ˉxξ+1=ˉxξ−ˉJ−1ΔˉW(ˉxξ)
or with
Δˉxξ=ˉJ−1ΔˉW(ˉxξ)
ˉxξ+1=ˉxξ−Δˉxξ
where superscript ξ indicates the iteration number and ˉJ![]() is a 2(n – 1) × 2(n – 1) matrix consisting of partial derivatives of mismatch powers with respect to the bus voltages. Note that all quantities are complex (thus the 2 in front of (n – 1)) and the swing bus voltage (magnitude and phase angle) is known (therefore n – 1). If ΔˉW(ˉxs)
is a 2(n – 1) × 2(n – 1) matrix consisting of partial derivatives of mismatch powers with respect to the bus voltages. Note that all quantities are complex (thus the 2 in front of (n – 1)) and the swing bus voltage (magnitude and phase angle) is known (therefore n – 1). If ΔˉW(ˉxs)![]() = 0 then
= 0 then
ˉx=ˉxs−ˉJ−1ΔˉW(ˉxs)=ˉxs.
The evaluation of Eq. 7-61 (the solution) is done by computer using triangular factorization and forward/backward substitution. This works for a few thousands of buses quite well. In case of hand calculations, where there are just a few buses, we use matrix inversion.