Angles
A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
—Euclid, The Elements, Definition 8
Geometric entities are of two kinds: those of a strictly qualitative nature, such as a point, a line, and a plane, and those that can be assigned a numerical value, a measure. To this last group belong a line segment, whose measure is its length; a planar region, associated with its area; and a rotation, measured by its angle.
There is a certain ambiguity in the concept of angle, for it describes both the qualitative idea of “separation” between two intersecting lines, and the numerical value of this separation—the measure of the angle. (Note that this is not so with the analogous “separation” between two points, where the phrases line segment and length make the distinction clear.) Fortunately we need not worry about this ambiguity, for trigonometry is concerned only with the quantitative aspects of line segments and angles.1
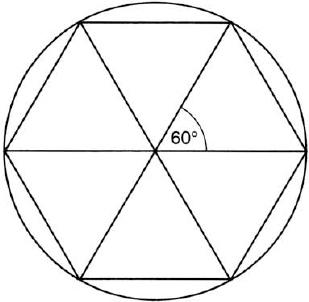
The common unit of angular measure, the degree, is believed to have originated with the Babylonians. It is generally assumed that their division of a circle into 360 parts was based on the closeness of this number to the length of the year, 365 days. Another reason may have been the fact that a circle divides naturally into six equal parts, each subtending a chord equal to the radius (fig. 4). There is, however, no conclusive evidence to support these hypotheses, and the exact origin of the 360-degree system may remain forever unknown.2 In any case, the system fitted well with the Babylonian sexagesimal (base 60) numeration system, which was later adopted by the Greeks and used by Ptolemy in his table of chords (see chapter 2).
As a numeration system, the sexagesimal system is now obsolete, but the division of a circle into 360 parts has survived—not only in angular measure but also in the division of an hour into 60 minutes and a minute into 60 seconds. This practice is so deeply rooted in our daily life that not even the ascendancy of the metric system was able to dispel it, and Florian Cajori’s statement in A History of Mathematics (1893) is still true today: “No decimal division of angles is at the present time threatened with adoption, not even in France [where the metric system originated].”3 Nevertheless, many hand-held calculators have a GRAD option in which a right angle equals 100 “gradians,” and fractional parts of a gradian are reckoned decimally.
FIG. 4. Regular hexagon inscribed in a circle.
The word degree originated with the Greeks. According to the historian of mathematics David Eugene Smith, they used the word μOιρα (moira), which the Arabs translated into daraja (akin to the Hebrew dar’ggah, a step on a ladder or scale); this in turn became the Latin de gradus, from which came the word degree. The Greeks called the sixtieth part of a degree the “first part,” the sixtieth part of that the “second part,” and so on. In Latin the former was called pars minuta prima (“first small part”) and the latter pars minuta secunda (“second small part”), from which came our minute and second.4
In more recent times the radian or circular measure has been universally adopted as the natural unit of angular measure. One radian is the angle, measured at the center of a circle, that subtends an arc length of one radius along the circumference (fig. 5). Since a complete circle encompasses 2π(≈ 6.28) radii along the circumference, and each of these radii corresponds to a central angle of 1 radian, we have 360° = 2π radians; hence 1 radian = 360°/2π ≈ 57.29°. The oft-heard statement that a radian is a more convenient unit than a degree because it is larger, and thus allows us to express angles by smaller numbers, is simply not true.5 The sole reason for using radians is that it simplifies many formulas. For example, a circular arc of angular width θ (where θ is in radians) subtends an arc length given by s = rθ; but if θ is in degrees, the corresponding formula is s = πrθ/180. Similarly, the area of a circular sector of angular width θ is A = r2θ/2 for θ in radians and A = πr2μ/360 for θ in degrees.6 The use of radians rids these formulas of the “unwanted” factor π/180.
FIG. 5. Radian angular measure.
Even more important, the fact that a small angle and its sine are nearly equal numerically—the smaller the angle, the better the approximation—holds true only if the angle is measured in radians. For example, using a calculator we find that the sine of one degree (sin 1°) is 0.0174524; but if the 1° is converted to radians, we have 1° = 2π/360π ≈ 0.0174533, so the angle and its sine agree to within one hundred thousandth. For an angle of 0.5° (again expressed in radians) the agreement is within one millionth, and so on. It is this fact, expressed as limθ→0(sin θ)/θ 1, that makes the radian measure so important in calculus.
The word radian is of modern vintage; it was coined in 1871 by James Thomson, brother of the famous physicist Lord Kelvin (William Thomson); it first appeared in print in examination questions set by him at Queen’s College in Belfast in 1873.7 Earlier suggestions were “rad” and “radial.”
No one knows where the convention of measuring angles in a counterclockwise sense came from. It may have originated with our familiar coordinate system: a 90° counterclockwise turn takes us from the positive x-axis to the positive y-axis, but the same turn clockwise will take us from the positive x-axis to the negative y-axis. This choice, of course, is entirely arbitrary: had the x-axis been pointing to the left, or the y-axis down, the natural choice would have been reversed. Even the word “clockwise” is ambiguous: some years ago I saw an advertisement for a “counterclockwise clock” that runs backward but tells the time perfectly correctly (fig. 6). Intrigued, I ordered one and hung it in our kitchen, where it never fails to baffle our guests, who are convinced that some kind of trick is being played on them!
FIG. 6. Counterclockwise clock.
NOTES AND SOURCES
1. However, the definiton of “angle” as a concept has always been problematic; see Euclid, The Elements, translated with introduction and commentary by Sir Thomas Heath (Annapolis, Md.: St. John’s College Press, 1947), vol. 1, pp. 176-181.
2. On this subject, see David Eugene Smith, History of Mathematics (1925; rpt. New York: Dover, 1953), vol. 2, pp. 229-232, and Florian Cajori, A History of Mathematics (1893, 2d ed,; New York: Macmitlan, 1919), pp. 5-6. Some scholars credit the 360-degree system to the Egyptians; see, for example, Elisabeth Achels, Of Time and the Calendar (New York: Hermitage House, 1955), p. 40.
3. Cajori, History of Mathematics, p. 484.
4. Smith, History of Mathematics, vol. 2, p. 232.
5. For example, in Morris Kline, Mathematics: A Cultural Approach (Reading, Mass.: Addison-Wesley, 1962), p. 500, we find the statement: “The advantage of radians over degrees is simply that it is a more convenient unit. Since an angle of 90° is of the same size as an angle of 1.57 radians, we have to deal only with 1.57 instead of 90 units.” It is surprising indeed to find this statement by an eminent mathematician such as Kline.
6. These formulas can easily be proved from proportional considerations: the circumference of a circle is to 2π radians as the arc length s is to θ; that is, 2πr/2π = s/θ, from which we get s = rθ. A similar argument leads to the formula A = r2θ/2.
7. Cajori, History of Mathematics, p. 484.