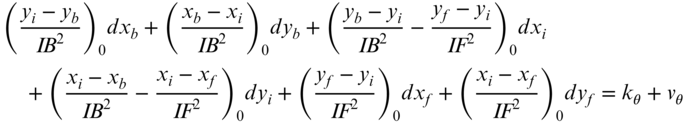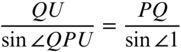Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

CHAPTER 15
ADJUSTMENT OF HORIZONTAL SURVEYS: TRIANGULATION

15.1 INTRODUCTION

Prior to the development of electronic distance measuring equipment and the global navigation satellite systems, triangulation was the preferred method for extending horizontal control over long distances. The positions of widely spaced stations were computed from observed angles and a minimal number of observed distances called baselines. This method was used extensively by the National Geodetic Survey in extending much of the national network. Triangulation is still used by many surveyors in establishing horizontal control, although surveys that combine trilateration (distance observations) with triangulation (angle observations) are more common. In this chapter, methods are described for adjusting triangulation networks using least squares method.

A least squares triangulation adjustment can use condition equations or observation equations written either in terms of azimuths or angles. In this chapter the observation equation method is presented. The procedure involves a parametric adjustment where the parameters are coordinates in a plane rectangular system such as state plane coordinates. In the examples, the specific types of triangulations known as intersections, resections, and quadrilaterals will be adjusted.

15.2 AZIMUTH OBSERVATION EQUATION

The azimuth equation in parametric form is

$images$ (15.1)

where $images$ , x_i and y_i are the coordinates of the occupied station I; x_j and y_j are the coordinates of the sighted station J; and C is a constant that depends on the quadrant in which point J lies as shown in Figure 15.1. From Figure 15.1, Table 15.1 can be constructed that relates the algebraic sign of the computed angle α in Equation (15.1) to the value of C and the value of the azimuth.

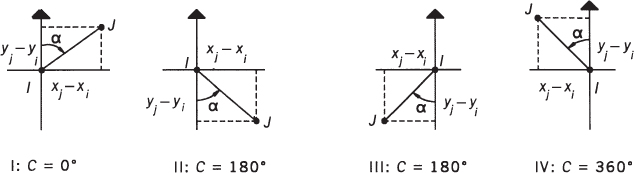
Illustration of Relationship between the azimuth and the computed angle, α. — **FIGURE 15.1** Relationship between the azimuth and the computed angle, α.

TABLE 15.1 Relationship between the Quadrant, C, and Azimuth

Quadrant	*Sign (x_j* − x_i)**	*Sign (y_j* − y_i )**	Sign α	C	Azimuth
I	+	+	+	0	α
II	+	−	−	180°	α + 180°
III	−	−	+	180°	α + 180°
IV	−	+	−	360°	α + 360°

15.2.1 Linearization of the Azimuth Observation Equation

Referring to Equation (15.1), the observation equation for an observed azimuth of line IJ is

$images$ (15.2)

where $images$ is the observed azimuth from station I to station $images$ , $images$ the residual in the observed azimuth, x_i and y_i the most probable values for the coordinates of station I, x_j, and y_j the most probable values for the coordinates of station J, and C a constant with a value based on Table 15.1. Equation (15.2) is a nonlinear function involving variables x_i, y_i, x_j, and y_j, which can be rewritten as

$images$ (15.3)

where

$images$

As discussed in Section 11.10, nonlinear equations such as (15.3) can be linearized and solved using a first‐order Taylor series approximation. The linearized form of Equation (15.3) is

$images$ (15.4)

where $images$ , $images$ , $images$ , and $images$ are the partial derivatives of F with respect to x_i, y_i, x_j, and y_j that are evaluated at the initial approximations and dx_i, dy_i, dx_j, and dy_j the corrections applied to the initial approximations after each iteration such that

$images$ (15.5)

To determine the partial derivatives of Equation (15.4) requires the prototype equation for the derivative of tan⁻¹(u) with respect to x, which is

$images$ (15.6)

Using Equation (15.6), the procedure for determining the $images$ is demonstrated as follows.

$images$ (15.7)

By employing similar procedures, the remaining partial derivatives are

$images$ (15.8)

where $images$ .

If Equations (15.7) and (15.8) are substituted into Equation (15.4) and the results then substituted into Equation (15.3), the following prototype azimuth equation is obtained.

$images$ (15.9)

Both

$images$

are evaluated using the approximate coordinate values of the unknown parameters.

15.3 ANGLE OBSERVATION EQUATION

Figure 15.2 illustrates the geometry for an angle observation. In Figure 15.2, B is the backsight station, I the instrument station, and F the foresight station. As shown in the figure, an angle observation equation can be written as the difference between two azimuth observations, and thus for clockwise angles:

$images$ (15.10)

Illustration of Relationship between an angle and two azimuths. — **FIGURE 15.2** Relationship between an angle and two azimuths.

where θ_bif is the observed clockwise angle, $images$ the residual in the observed angle, x_b and y_b the most probable values for the coordinates of the backsight station B, x_i and y_i the most probable values for the coordinates of the instrument station I, x_f and y_f the most probable values for the coordinates of the foresighted station F, and D a constant that depends on the quadrants in which the backsight and foresight occur. This term can be computed as the difference between the C terms from Equation (15.1) as applied to the backsight and foresight azimuths; that is,

$images$

Equation (15.10) is a nonlinear function of x_b, y_b, x_i, y_i, x_f, and y_f that can be rewritten as

$images$ (15.11)

where

$images$

Equation (15.11) expressed as a linearized, first‐order Taylor series expansion is

$images$ (15.12)

where $images$ , $images$ , $images$ , $images$ , $images$ , and $images$ are the partial derivatives of F with respect to x_b, y_b, x_i, y_i, x_f, and y_f, respectively.

Evaluating partial derivatives of the function F and substituting into Equation (15.12), then substituting into Equation (15.11), results in the following equation.

$images$ (15.13)

where

$images$

are evaluated at the approximate values for the unknown coordinates. Formulating the linearized angle observation equation can be thought of as the difference in two linearized azimuth equations. Using Equation (15.9) as a guide, the difference between the foresight and backsight azimuth is

$images$ (15.14)

Rearranging and regrouping Equation (a) yields Equation (15.13). This is left as an exercise for the reader.

In formulating the angle observation equation, remember that I is always assigned to the instrument station, B the backsight, and F the foresight station. This station designation must be strictly followed in employing prototype Equation (15.13) as will be demonstrated in the numerical examples that follow, and reproduced in the spreadsheet file Chapter 15.xls. As each is discussed, the reader may wish to refer to this file to see how the problem is implemented in a spreadsheet. Additionally, the file C15.xmcd demonstrates these examples in the higher‐level programming language of Mathcad. These files can be found on the companion website for this book.

15.4 ADJUSTMENT OF INTERSECTIONS

When an unknown station is visible from two or more existing control stations, the angle intersection method is one of the simplest and sometimes most practical ways for determining the horizontal position of a station. For a unique computation, the method requires the observation of at least two horizontal angles from two control points. For example, angles θ₁ and θ₂ observed from control stations R and S in Figure 15.3 will enable a unique computation for the position of station U. If additional control is available, the computations for the unknown station's position can be strengthened by observing redundant angles such as angles θ₃ and θ₄ in Figure 15.3 and applying the method of least squares. In that case, for each of the four independent angles, a linearized observation equation is written in terms of the two unknown coordinates x_u and y_u.

Illustration of Intersection example. — **FIGURE 15.3** Intersection example.

EXAMPLE 15.1

Using the method of least squares, compute the most probable coordinates of station U in Figure 15.3. The following equally weighted horizontal angles were observed from control stations R, S, and T:

$images$

The coordinates for the control stations R, S, and T are:

$images$

SOLUTION

Step 1: Determine initial approximations for the coordinates of station U.
1. Using the coordinates of stations R and S, the distance RS is computed as
  $images$
2. From the coordinates of stations R and S, the azimuth of the line between R and S is determined using Equation (15.2). Then the initial azimuth of line RU is computed by subtracting θ₁ from the azimuth of line RS.
  $images$
3. Using the law of sines with triangle RUS, an initial length for RU₀ can be calculated as
  $images$
4. Using the azimuth and distance for RU₀ computed in steps 1(b) and 1(c), initial coordinates for station U are computed as
  $images$
5. Using the appropriate coordinates, the initial distances for SU and TU are calculated as
  $images$
Step 2: Formulate the linearized equations. As in the trilateration adjustment, control station coordinates are held fixed during the adjustment by assigning zeros to their dx and dy values. Thus, these terms drop out of prototype Equation (15.13). In forming the observation equations, b, i, and f are assigned to the backsight, instrument, and foresight stations, respectively, for each angle. For example, with angle θ₁, B, I, and F are replaced by U, R, and S, respectively. By combining the station substitutions shown in Table 15.2 with prototype Equation (15.13), the following observation equations are written for the four observed angles.
$images$

TABLE 15.2 Substitutions

Angle	B	I	F
θ₁	U	R	S
θ₂	R	S	U
θ₃	U	S	T
θ₄	S	T	U

Substituting the appropriate values into Equations (15.14) and multiplying the left side of the equations by ρ to achieve unit consistency,¹ the following J and K matrices are formed.

$images$

Notice that the initial coordinates for $images$ and $images$ were calculated using θ₁ and θ₂, and thus their K‐matrix values are zero for the first iteration. These values will change in subsequent iterations.

Step 3: Matrix solution. The least squares solution is found by applying Equation (11.37).
$images$
Step 4: Add the corrections to the initial coordinates for station U.
$images$ (15.15)
Step 5: Repeat Steps 2 through 4 until negligible corrections occur. The next iteration produced negligible corrections, and thus Equations (15.15) produced the final adjusted coordinates for station U.
Step 6: Compute post‐adjustment statistics. The residuals for the angles are
$images$

The reference standard deviation for the adjustment is computed using Equation (12.14) as

$images$

The estimated errors for the adjusted coordinates of station U, given by Equation (13.24), are

$images$

The estimated error in the position of station U is given by

$images$

15.5 ADJUSTMENT OF RESECTIONS

Resection is a method used for determining the unknown horizontal position of an occupied station by observing a minimum of two horizontal angles to a minimum of three stations whose horizontal coordinates are known. If more than three stations are available, redundant observations are obtained and the position of the unknown occupied station can be computed using the least squares method. Like intersection, resection is suitable for locating an occasional station and is especially well adapted over inaccessible terrain. This method is commonly used for orienting total station instruments in locations favorable for staking projects by radiation using coordinates.

Consider the resection position computation for the occupied station U of Figure 15.4 having observed the three horizontal angles shown between stations P, Q, R, and S whose positions are known. To determine the position of station U, two angles could be observed. The third angle provides a check and allows a least squares solution for computing the coordinates of station U.

Illustration of Resection example. — **FIGURE 15.4** Resection example.

Using prototype Equation (15.13), a linearized observation equation can be written for each angle. In this problem, the vertex station is occupied and is the only unknown station. Thus, all coefficients in the Jacobian matrix follow the form used for the coefficients of dx_i and dy_i in prototype Equation (15.13). The method of least squares yields corrections, dx_u and dy_u, which gives the most probable coordinate values for station U.

15.5.1 Computing Initial Approximations in the Resection Problem

In Figure 15.4, only two angles are necessary to determine the coordinates of station U. Using stations P, Q, R, and U, a procedure to find the station U's approximate coordinate values is

Step 1: Let
$images$ (15.16)
Step 2: Using the sine law with triangle PQU,
$images$ (a)

and with triangle URQ,

$images$ (b)
Step 3: Solving Equations (a) and (b) for QU and setting the resulting equations equal to each other yields
$images$ (c)
Step 4: From Equation (c), let H be defined as
$images$ (15.17)
Step 5: From Equation (15.16),
$images$ (d)
Step 6: Solving Equation (15.17) for the sin ∠QPU, and substituting Equation (d) into the result yields
$images$ (e)
Step 7: From trigonometry:
$images$

Applying this relationship to Equation (e),

$images$ (f)

(g) $images$

Step 8: Dividing Equation (g) by cos ∠URQ and rearranging yields
$images$ (h)
Step 9: Solving Equation (h) for ∠URQ gives
$images$ (15.18)
Step 10: From Figure 15.4,
$images$ (15.19)
Step 11: Again applying the sine law yields
$images$ (15.20)
Step 12: Finally, the initial coordinates for station U are
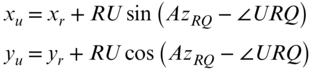$images$ (15.21)

EXAMPLE 15.2

The following data are obtained for Figure 15.4. Control stations P, Q, R, and S have the following (x, y) coordinates: P (1303.599, 1458.615), Q (1636.436, 1310.468), R (1503.395, 888.362), and S (1506.262, 785.061). The observed values for angles 1, 2, and 3 with standard deviations are

Backsight	Occupied	Foresight	Angle	S (″)
P	U	Q	30°29′33″	±5
Q	U	R	38°30′31″	±6
R	U	S	10°29′57″	±6

What are the most probable coordinates of station U?

SOLUTION

Using the procedures described in Section 15.4.1, the initial approximations for the coordinates of station U are:

From Equation (15.10),
$images$
Substituting the appropriate angular values into Equation (15.16), yields
$images$
Substituting the appropriate station coordinates into Equation (14.1) yields
$images$
Substituting the appropriate values into Equation (15.17) yields H as
$images$
Substituting previously determined G and H into Equation (15.18), ∠URQ is computed as
$images$
Substituting the value of ∠URQ into Equation (15.19), ∠RQU is determined to be
$images$
From Equation (15.20), RU is
$images$
Using Equation (15.1), the azimuth of RQ is
$images$
From Figure 15.4, Az_RU is computed as
$images$
Using Equation (15.21), the coordinates for station U are
$images$

For this problem, using prototype Equation (15.13), the J and K matrices are

$images$

Also, the weight matrix W is a diagonal matrix composed of the inverses of the variances for the observed angles, or

$images$

Using the data given for the problem, together with the computed initial approximations, numerical values for the matrices were calculated and the adjustment performed using program ADJUST. A file named Adjust file for Example 15‐2.dat is on the companion website. The following results were obtained after two iterations. The reader is encouraged to adjust these example problems using both the MATRIX and ADJUST programs supplied.

ITERATION 1 
J MATRIX                K MATRIX   X MATRIX 
======================= ========= ========= 
 184.993596   54.807717 -0.203359 -0.031107 
 214.320813  128.785353 -0.159052  0.065296 
  59.963802  -45.336838 -6.792817  
ITERATION 2 
J MATRIX                K MATRIX  X MATRIX 
======================= ========= ========= 
 185.018081   54.771738  1.974063  0.000008 
 214.329904  128.728773 -1.899346  0.000004 
 59.943758   -45.340316 -1.967421  
INVERSE MATRIX 
======================= 
 0.00116318 -0.00200050 
-0.00200050  0.00500943  
***************** 
Adjusted stations 
***************** 
Station X              Y          Sx          Sy 
================================================= 
  U    999.999     1,000.025    0.0206    0.0427  
*************************** 
Adjusted Angle Observations 
*************************** 
    Station  Station     Station 
Backsighted Occupied Foresighted      Angle     V        S (″) 
=============================================================== 
     P         U         Q         30°29′31″   -2.0″      2.3 
     Q         U         R         38°30′33″    1.9″      3.1 
     R         U         S         10°29′59″    2.0″      3.0  
********************** 
Adjustment Statistics 
********************** 
Redundancies = 1 
Reference Variance = 0.3636 
Reference So = ±0.60

15.6 ADJUSTMENT OF TRIANGULATED QUADRILATERALS

The quadrilateral is the basic figure for triangulation. Procedures like those used for adjusting intersections and resections are also used to adjust this figure. In fact, the parametric adjustment using the observation equation method can be applied to any triangulated geometric figure, regardless of its shape.

The procedure for adjusting a quadrilateral consists in first using a minimum number of the observed angles to solve triangles and computing initial values for the coordinates. Corrections to these initial coordinates are then calculated by applying the method of least squares. The procedure is iterated until the solution converges. This yields the most probable coordinate values. A statistical analysis of the results is then made. The following example illustrates the procedure.

EXAMPLE 15.3

The following observations are supplied for Figure 15.5. Adjust this figure by the method of least squares. Assume equal weights for the angles. The observed angles (assume equal weights) are as follows:

$images$

FIGURE 15.5 Quadrilateral example.

The fixed coordinates are

$images$

SOLUTION

The coordinates of station B and C are to be computed in this adjustment. The Jacobian matrix has the form shown in Table 15.3. The subscripts b, i, and f of the dx's and dy's in Table 15.3 indicate whether stations B and C are the backsight, instrument, or foresight station in Equation (15.13). Of course, in developing the coefficient matrix, the appropriate station coordinate substitutions must be made to obtain each coefficient.

TABLE 15.3 Structure of the Coefficient or J Matrix in Example 15.3

	Unknowns
Angle	*dx_b*	*dy_b*	*dx_c*	*dy_c*
1	dx(b)	dy(b)	dx(f)	dy(f)
2	0	0	dx(b)	dy(b)
3	dx(i)	dy(i)	dx(b)	dy(b)
4	dx(i)	dy(i)	0	0
5	0	0	dx(i)	dy(i)
6	dx(f)	dy(f)	dx(i)	dy(i)
7	dx(f)	dy(f)	0	0
8	dy(b)	dy(b)	dx(f)	dy(f)

The reader is encouraged to review this example in the spreadsheet file Chapter 15.xls. In this spreadsheet the cells are named, which allows the coefficients to be entered in an understandable manner. Additionally, the matrices are setup in a manner that allows them to be copied directly into MATRIX. In MATRIX, the unweighted least squares adjustment option in the numerical operations menu is used to quickly obtain solution. The resulting X matrix is copied into the spreadsheet where it is placed in the appropriate cells to update the coordinates for stations B and C. Figure 15.4 shows the portion of the spreadsheet where the final coordinates are updated. Notice how the initial coordinate values are summed to the cell labeled as Final. Once the coordinates are updated, the J and K matrices are updated immediately. This process is repeated until the final solution is confirmed in the second iteration. Following the solution convergence, the $images$ , Sxx, Sll, and reference variance matrices are copied into the spreadsheet. These matrices are used to compute the post‐adjustment statistics shown in Figures 15.6 and 15.7.

FIGURE 15.6 Portion of the spreadsheet for Example 15.3.

FIGURE 15.7 Portion of the spreadsheet for Example 15.3.

The following self‐explanatory computer listing is from ADJUST. It was created using the file Adjust file for Example 15‐3.dat, which is on the companion website. As shown, a single iteration was satisfactory to achieve convergence, since the second iteration produced negligible corrections. Residuals, adjusted coordinates, their estimated errors, and adjusted angles are tabulated at the end of the listing.

******************************************* 
Initial approximations for unknown stations 
******************************************* 
Station           X           Y 
=================================== 
         B    2,403.600  16,275.400 
         C    9,649.800  24,803.500  
Control Stations 
∼∼∼∼∼∼∼∼∼∼∼∼∼∼∼∼∼ 
Station           X          Y 
=================================== 
         A    9,270.330  8,448.900 
         D   15,610.580  8,568.750  
******************* 
Angle Observations 
******************* 
     Station  Station     Station 
 Backsighted Occupied Foresighted                Angle 
======================================================= 
           B        A           C            42°35′29.0″ 
           C        A           D            87°35′10.6″ 
           C        B           D            79°54′42.1″ 
           D        B           A            18°28′22.4″ 
           D        C           A            21°29′23.9″ 
           A        C           B            39°01′35.4″ 
           A        D           B            31°20′45.8″ 
           B        D           C            39°34′27.9″  
Iteration 1,
J Matrix                                         K MATRIX   X MATRIX 
-----------------------------------------------  ---------  -------------- 
  14.891521   -13.065362   12.605250   -0.292475  -1.811949  1  -0.011149 
   0.000000     0.000000  -12.605250    0.292475  -5.801621  2   0.049461 
  20.844399    -0.283839  -14.045867   11.934565   3.508571  3   0.061882 
   8.092990     1.414636    0.000000    0.000000   1.396963  4   0.036935 
   0.000000     0.000000    1.409396   -4.403165  -1.833544 
  14.045867    11.934565    1.440617  -11.642090   5.806415 
   6.798531    11.650726    0.000000    0.000000  -5.983393 
   6.798531   -11.650726   11.195854    4.110690   1.818557  
Iteration 2,
J Matrix                                         K MATRIX   X MATRIX 
-----------------------------------------------  ---------  -------------- 
  14.891488   -13.065272   12.605219   -0.292521  -2.100998  1   0.000000 
   0.000000     0.000000  -12.605219    0.292521  -5.032381  2  -0.000000 
  20.844296    -0.283922  -14.045752   11.934605   4.183396  3   0.000000 
   8.092944     1.414588    0.000000    0.000000   1.417225  4  -0.000001 
   0.000000     0.000000    1.409357   -4.403162  -1.758129 
  14.045752    11.934605    1.440533  -11.642083   5.400377 
   6.798544    11.650683    0.000000    0.000000  -6.483846 
   6.798544   -11.650683   11.195862    4.110641   1.474357  
INVERSE MATRIX 
-------------- 
 0.00700  -0.00497  0.00160  -0.01082 
-0.00497   0.00762  0.00148   0.01138 
 0.00160   0.00148  0.00378   0.00073 
-0.01082   0.01138  0.00073   0.02365  
****************** 
Adjusted stations 
****************** 
Station          X           Y           Sx       Sy 
======================================================= 
        B    2,403.589   16,275.449    0.4690   0.4895 
        C    9,649.862   24,803.537    0.3447   0.8622  
*************************** 
Adjusted Angle Observations 
*************************** 
    Station  Station     Station 
Backsighted Occupied Foresighted       Angle    V           S 
============================================================ 
          B        A           C    42°35′31.1″   2.10″ 3.65 
          C        A           D    87°35′15.6″   5.03″ 4.33 
          C        B           D    79°54′37.9″  -4.18″ 4.29 
          D        B           A    18°28′21.0″  -1.42″ 3.36 
          D        C           A    21°29′25.7″   1.76″ 3.79 
          A        C           B    39°01′30.0″  -5.40″ 4.37 
          A        D           B    31°20′52.3″   6.48″ 4.24 
          B        D           C    39°34′26.4″  -1.47″ 3.54  
                   ******************************************** 
                                      Adjustment Statistics 
                   ********************************************  
                                          Iterations = 2 
                                         Redundancies = 4 
                                Reference Variance = 31.42936404 
                                       Reference So = ±5.6062 
                                           Convergence!

PROBLEMS

Note: Partial answers to problems marked with an asterisk can be found in Appendix H.

*15.1 Given the following observations and control station coordinates to accompany figure, what are the most probable coordinates for station E using an unweighted least squares adjustment?

Control Stations
Station	X (ft)	Y (ft)
A	10,000.00	10,000.00
B	11,498.58	10,065.32
C	12,432.17	11,346.19
D	11,490.57	12,468.51

Angle Observations
Backsight (b)	Occupied (i)	Foresight (f)	Angle	S (″)
E	A	B	90°59′57″	±3.3
A	B	E	40°26′02″	±3.7
E	B	C	88°08′55″	±3.9
B	C	E	52°45′02″	±3.7
E	C	D	51°09′55″	±3.8
C	D	E	93°13′14″	±4.0

Illustration of a stretched square. — **FIGURE P15.1**

15.2 Repeat Problem 15.1 using a weighted least squares adjustment with weights of 1/S² for each angle. What are the:
1. (a) Most probable coordinates for station E and their standard deviations?
2. (b) Reference standard deviation of unit weight?
3. (c) Adjusted angles, their residuals, and standard deviations?
15.3 Given the following observations and control station coordinates to accompany Figure 15.3, what are the:
1. (a) Most probable coordinates for station E and their standard deviations?
2. (b) Reference standard deviation of unit weight?
3. (c) Adjusted angles, their residuals, and standard deviations?
Control Stations

Station Easting (m) Northing (m)

R 6,735.656 6,061.097

S 6,894.607 5,517.132

T 6,693.269 4,920.183

Angle Observations

Backsight (b) Occupied (i) Foresight (f) Angle S (″)

U R S 49°07′42″ ±4.6

R S U 103°13′02″ ±4.9

U S T 111°42′34″ ±4.6

S T U 41°26′28″ ±4.3
*15.4 Given the following observed angles and control coordinates for the resection problem of Figure 15.4.

$images$

Assuming equally weighted angles, what are the most probable coordinates for station U?

Control Stations

Station X (ft) Y (ft)

P 9000.00 9000.00

Q 9000.00 7500.00

R 9000.00 2500.00

S 9000.00 1200.00
15.5 If the estimated standard deviations for the angles in Problem 15.4 are S₁ = ±4.5″, S₂ = ±4.3″, and S₃ = ±3.6″, what are the:
1. (a) Most probable coordinates for station U and their standard deviations?
2. *(b) Reference standard deviation of unit weight?
3. (c) Adjusted angles, their residuals, and standard deviations?
15.6 Repeat Problem 15.5 using the following data.

Control Stations

Station X (ft) Y (ft)

P 8,593.99 8,170.60

Q 8,812.99 7,566.58

R 9,145.02 7,170.97

S 9,014.33 6,711.78

Angle Observations

Backsight (b) Occupied (i) Foresight (f) Angle S (″)

P U Q 22°52′35″ ±5.4

Q U R 20°49′45″ ±5.0

R U S 18°54′10″ ±6.2
15.7 Using approximate (x, y) coordinates for station E of (24,514.027, 23,409.472), and given the following control coordinates and observed angles for an intersection problem:

Control Stations

Station X (m) Y (m)

A 643.154 8,213.066

B 1,093.916 37,422.484

C 37,515.536 37,061.874

D 39,408.739 7,491.846

Angle Observations

Backsight Occupied Foresight Angle S (″)

E A D 33°32′48″ ±3.5

E B A 59°59′24″ ±3.5

E C B 46°57′58″ ±3.5

E D C 39°26′00″ ±3.5

What are the:
1. (a) Most probable coordinates for station E and their standard deviations?
2. (b) Reference standard deviation of unit weight?
3. (c) Adjusted angles, their residuals, and standard deviations?

Control Stations
R	6,735.656	6,061.097
S	6,894.607	5,517.132
T	6,693.269	4,920.183

Angle Observations
U	R	S	49°07′42″	±4.6
R	S	U	103°13′02″	±4.9
U	S	T	111°42′34″	±4.6
S	T	U	41°26′28″	±4.3

Control Stations
P	9000.00	9000.00
Q	9000.00	7500.00
R	9000.00	2500.00
S	9000.00	1200.00

Control Stations
P	8,593.99	8,170.60
Q	8,812.99	7,566.58
R	9,145.02	7,170.97
S	9,014.33	6,711.78

Angle Observations
P	U	Q	22°52′35″	±5.4
Q	U	R	20°49′45″	±5.0
R	U	S	18°54′10″	±6.2

Control Stations
A	643.154	8,213.066
B	1,093.916	37,422.484
C	37,515.536	37,061.874
D	39,408.739	7,491.846

Angle Observations
E	A	D	33°32′48″	±3.5
E	B	A	59°59′24″	±3.5
E	C	B	46°57′58″	±3.5
E	D	C	39°26′00″	±3.5

15.8 The following control station coordinates, observed angles and standard deviations apply to the quadrilateral in Figure 15.5.

Control Stations			Initial Approximations
Station	X (ft)	Y (ft)	Station	X (ft)	Y (ft)
A	1536.43	210.86	B	176.67	2801.09
D	3798.06	205.98	C	2355.54	2826.52

Angle Observations
Backsight	Occupied	Foresight	Angle	S (″)
B	A	C	45°24′8″	±3.7
C	A	D	72°44′00″	±3.7
C	B	D	36°17′38″	±3.7
D	B	A	26°40′40″	±3.6
D	C	A	46°13′13″	±3.7
A	C	B	71°56′40″	±3.7
A	D	B	35°30′04″	±3.7
B	D	C	25°32′33″	±3.6

Do a weighted adjustment using the standard deviations to calculate weights. What are the

*(a) Most probable coordinates for stations B and C and their standard deviations?
(b) Reference standard deviation of unit weight?
(c) Adjusted angles, their residuals, and standard deviations?

15.9 For the accompanying figure and the following observations, perform a weighted least squares adjustment.

(a) Station coordinates and standard deviations.
(b) Angles, their residuals, and standard deviations.

Control Stations			Initial Approximations
Station	X (m)	Y (m)	Station	X (m)	Y (m)
A	600.544	966.236	C	3969.023	4112.018
B	1061.624	4043.173	D	3860.927	955.098

Angle Observations
Backsight	Occupied	Foresight	Angle	S (″)
B	A	C	38°26′08″	±2.2
C	A	D	43°14′15″	±2.1
C	B	D	49°09′52″	±2.2
D	B	A	50°42′47″	±2.2
D	C	A	44°59′51″	±2.2
A	C	B	41°41′08″	±2.2
B	D	C	44°09′07″	±2.2
A	D	B	47°36′44″	±2.2

Illustration of a geometrical figure. — **FIGURE P15.9**

15.10 Do Problem 15.9 using the additional horizon closure angles listed below.

Backsight Occupied Foresight Angle S (″)

D A B 278°19′38″ ±2.2

A B C 260°07′18″ ±2.2

B C D 273°19′38″ ±2.2

C D A 268°14′03″ ±2.2
1. (a) Station coordinates and standard deviations.
2. (b) Angles, their residuals, and standard deviations.
3. (c) Compare and discuss any differences or similarities between these results and those obtained in Problem 15.9.

Backsight	Occupied	Foresight	Angle	S (″)
D	A	B	278°19′38″	±2.2
A	B	C	260°07′18″	±2.2
B	C	D	273°19′38″	±2.2
C	D	A	268°14′03″	±2.2

15.11 The following observations were obtained for a triangulation chain shown in the accompanying figure.

Control Stations			Initial Approximations
Station	X (m)	Y (m)	Station	X (m)	Y (m)
A	1718.871	632.095	C	1668.571	1310.429
B	2191.570	715.709	D	2139.109	1296.242
G	1590.370	2560.743	E	1617.479	1649.217
H	2076.006	2597.745	F	2028.688	1934.566

Angle Observations
B	I	F	Angle	S (″)	B	I	F	Angle	S (″)
C	A	D	36°33′50″	±4.1	D	E	C	47°20′12″	±7.0
D	A	B	47°38′41″	±5.1	F	E	D	68°50′37″	±5.4
A	B	C	58°42′10″	±5.2	D	F	C	39°48′02″	±4.4
C	B	D	36°09′45″	±4.5	C	F	E	25°15′23″	±5.1
D	C	B	46°56′47″	±5.2	H	E	F	29°26′35″	±4.7
B	C	A	37°05′14″	±4.1	G	E	H	27°30′09″	±3.1
B	D	A	37°29′19″	±4.5	E	F	G	89°45′54″	±5.1
A	D	C	59°24′16″	±5.2	G	F	H	39°04′24″	±4.2
E	C	F	38°33′24″	±6.8	H	G	F	59°21′56″	±5.2
F	C	D	61°44′32″	±5.4	F	G	E	33°17′14″	±3.6
C	D	E	32°21′36″	±5.5	F	H	E	21°43′05″	±3.8
E	D	F	46°05′58″	±4.7	E	H	G	59°50′37″	±4.8

Use ADJUST to perform a weighted least squares adjustment. Tabulate the final adjusted

(a) Station coordinates and their standard deviations.
(b) Angles, their residuals, and standard deviations.

Illustration of a triangulation chain. — **FIGURE P15.11**

15.12 Add the following horizon closure angles to the data in Problem 15.11 and use the program ADJUST to perform the adjustment.

B	I	F	Angle	S (″)
B	A	C	275°47′22″	±5.6
A	C	E	175°40′06″	±7.3
C	E	G	186°52′52″	±6.9
E	G	H	267°20′44″	±5.2
G	H	F	278°26′18″	±5.6
H	F	D	166°06′12″	±5.0
F	D	B	184°39′06″	±5.3
D	B	A	265°07′57″	±6.0

(a) Station coordinates and their standard deviations.
(b) Angles, their residuals, and standard deviations.
(c) Compare and discuss any differences or similarities between these results and those obtained in Problem 15.11.

15.13 Using the control coordinates from Problem 14.3 and the following angle observations, compute the least squares solution and tabulate the final adjusted

(a) Station coordinates and their standard deviations.
(b) Angles, their residuals, and standard deviations.

Angle Observations
Backsight	Occupied	Foresight	Angle	S (″)
B	A	C	60°00′34″	±3.3
C	A	D	59°59′23″	±2.9
C	B	D	43°04′22″	±2.8
C	B	A	79°07′27″	±3.4
D	C	A	58°17′31″	±2.9
A	C	B	40°51′51″	±3.0
A	D	B	23°56′43″	±2.7
B	D	C	37°46′19″	±2.7

15.14 The following observations were obtained for a triangulation chain.

Control Stations			Initial Approximations
Station	X (ft)	Y (ft)	Station	X (ft)	Y (ft)
A	3,190.04	8,433.74	B	3,711.26	10,408.62
D	3,671.87	14,314.29	C	3,981.71	12,055.36
H	7,475.32	8,437.20	E	5,491.00	9,032.76
K	7,590.44	14,142.31	F	5,509.17	11,145.10
			G	5,519.02	13,102.09
			I	7,213.18	10,377.56
			J	7,311.66	12,317.91

Angle Observations
B	I	F	Angle	S (″)	B	I	F	Angle	S (″)
B	A	E	60°37′23″	±1.7	J	F	I	57°17′59″	±1.8
E	B	A	67°04′41″	±1.7	I	F	E	66°14′38″	±1.8
F	B	E	59°58′55″	±1.7	E	F	B	67°13′52″	±1.8
C	B	F	58°23′48″	±1.9	A	E	B	52°17′56″	±1.6
F	C	B	68°32′07″	±2.0	B	E	F	52°47′11″	±1.7
G	C	F	65°02′32″	±1.9	F	E	I	51°31′17″	±1.7
D	C	G	63°33′32″	±1.8	I	E	H	51°41′29″	±1.7
G	D	C	48°54′53″	±1.7	H	E	A	148°42′06″	±1.7
D	G	K	120°03′38″	±1.7	E	H	I	65°35′58″	±1.8
K	G	J	50°17′30″	±1.7	H	I	E	59°42′34″	±1.8
J	G	F	66°39′44″	±1.8	E	I	F	62°14′01″	±1.8
F	G	C	55°27′39″	±1.8	F	I	J	68°39′25″	±1.9
C	G	D	67°31′30″	±1.8	I	J	F	54°02′38″	±1.8
B	F	C	53°04′04″	±1.9	F	J	G	56°40′36″	±1.8
C	F	G	59°29′48″	±1.9	G	J	K	75°03′42″	±1.9
G	F	J	56°39′38″	±1.8	J	K	G	54°38′50″	±1.8

Use ADJUST to perform a weighted least squares adjustment. Tabulate the final adjusted

(a) Station coordinates and their standard deviations.
(b) Angles, their residuals, and standard deviations.

15.15 Add the following horizon closure angles to the data in Problem 15.14 and use the program ADJUST to perform the adjustment.

B	I	F	Angle	S (″)	B	I	F	Angle	S (″)
E	A	B	299°22′38″	±1.7	G	K	J	305°21′11″	±1.8
A	B	C	174°32′30″	±2.0	K	J	I	174°13′19″	±1.9
B	C	D	162°51′49″	±1.9	J	I	H	169°24′02″	±1.9
C	D	G	311°05′06″	±1.7	I	H	E	294°24′00″	±1.8

(a) Station coordinates and their standard deviations.
(b) Angles, their residuals, and standard deviations.
(c) Compare the results of the adjustment with that of Problem 15.14.

Use the ADJUST software to do the following problems.

15.16 Problems 15.2.
15.17 Problems 15.4.
15.18 Problem 15.5.
15.19 Problems 15.6.
15.20 Problems 15.8.
15.21 Show that Equation (a) can be rearranged and regrouped to match Equation (15.13).

PROGRAMMING PROBLEMS

15.22 Write a computational program that computes the coefficients for prototype Equations (15.9) and (15.13), and their k values given the coordinates of the appropriate stations. Use this program to determine the matrix values necessary to do Problem 15.6.
15.23 Prepare a computational program that reads a file of station coordinates, observed angles, and their standard deviations and then
1. (a) Writes the data to a file in a formatted fashion.
2. (b) Computes the J, K, and W matrices.
3. (c) Writes the matrices to a file that is compatible with the MATRIX program.
4. (d) Test this program with Problem 15.6.
15.24 Write a computational program that reads a file containing the J, K, and W matrices and then
1. (a) Writes these matrices in a formatted fashion.
2. (b) Performs one iteration of either a weighted or unweighted least squares adjustment of Problem 15.6.
3. (c) Writes the matrices used to compute the solution and the corrections to the station coordinates in a formatted fashion.
15.25 Write a computational program that reads a file of station coordinates, observed angles, and their standard deviations and then
1. (a) Writes the data to a file in a formatted fashion.
2. (b) Computes the J, K, and W matrices.
3. (c) Performs either a relative or equal‐weight least squares adjustment of Problem 15.6.
4. (d) Writes the matrices used to compute the solution, and tabulates the final adjusted station coordinates and their estimated errors, and the adjusted angles together with their residuals and their estimated errors.
15.26 Prepare a computational program that solves the resection problem. Use this program to compute the initial approximations for Problem 15.3.

NOTE

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for CHAPTER 15: ADJUSTMENT OF HORIZONTAL SURVEYS: TRIANGULATION

Create new playlist

Sign In

Sign Up

15.1 INTRODUCTION

15.2 AZIMUTH OBSERVATION EQUATION

15.2.1 Linearization of the Azimuth Observation Equation

15.3 ANGLE OBSERVATION EQUATION

15.4 ADJUSTMENT OF INTERSECTIONS

15.5 ADJUSTMENT OF RESECTIONS

15.5.1 Computing Initial Approximations in the Resection Problem

15.6 ADJUSTMENT OF TRIANGULATED QUADRILATERALS

PROBLEMS

PROGRAMMING PROBLEMS

NOTE

Table of Contents for
CHAPTER 15: ADJUSTMENT OF HORIZONTAL SURVEYS: TRIANGULATION