B.1 INTRODUCTION

As stated in Appendix A, an advantage offered by matrix algebra is its adaptability to computer usage. Using matrix algebra, large systems of simultaneous linear equations can be programmed for general computer solution using only a few systematic steps. For example, the simplicities of programming matrix additions and multiplications were presented in Section A.9. To solve a system of equations using matrix methods, it is first necessary to define and compute the inverse matrix.

B.2 INVERSE MATRIX

If a square matrix is nonsingular (its determinant is not zero), it possesses an inverse matrix. When a system of simultaneous linear equations consisting of n equations and involving n unknowns is expressed as AX = B, the coefficient matrix (A) is a square matrix of dimensions n × n. Consider this system of linear equations

(B.1)

The inverse of matrix A, symbolized as A⁻¹, is defined as

(B.2)

where I is the identity matrix. Premultiplying both sides of matrix Equation (B.1) by A⁻¹ gives

Reducing yields

(B.3)

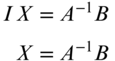
Thus, the inverse is used to find the matrix of unknowns, X. The following points should be emphasized regarding matrix inversions:

1. Square matrices have inverses, with the exception noted below.
2. When the determinant of a matrix is zero, the matrix is said to be singular and its inverse cannot be found.
3. The inversion of even a small matrix is a tedious and time-consuming operation when done by hand. However, when done by a computer, the inverse can be found quickly and easily.

B.3 THE INVERSE OF A 2 × 2 MATRIX

Several general methods are available to find a matrix inverse. Two shall be considered herein. However, before proceeding with general cases consider the specific case of finding the inverse for a 2 × 2 matrix using simple elementary matrix operations. Let any 2 × 2 matrix be symbolized as A. Also, let

By applying Equation (B.2) and recalling the definition of an identity matrix I as given in Section A.4, it is possible to calculate w, x, y, and z in terms of a, b, c, and d of A⁻¹. Substituting in the appropriate values gives

By matrix multiplication

(a)

(b)

(c)

(d)

The determinant of A is symbolized as and equal to ad − bc.

Thus, for any 2 × 2 matrix composed of the elements 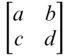, its inverse is simply

B.4 INVERSES BY ADJOINTS

The inverse of A can be found using the method of adjoints with the following equation:

(B.4)

The adjoint of A is obtained by first replacing each matrix element by its signed minor or cofactor, and then transposing the resultant matrix. The cofactor of element a_ij equals (−1)^i+j times the numerical value of the determinant for the remaining elements after row i and column j have been removed from the matrix. This procedure is illustrated in Figure B.1 where the cofactor of a₁₂ is

Using this procedure, the inverse of the following A matrix is found:

For this A matrix, the cofactors are calculated as follows:

Following the procedure above, the matrix of cofactors is

Transposing this cofactor matrix produces the following adjoint of A:

The determinant of A is the sum of the products of the elements in the first row of the original matrix times their respective cofactors. Since the cofactors were already obtained in the previous step, this simplifies to

The inverse of A is now calculated as

Again, a check on the arithmetical work is obtained by using the definition of an inverse:

B.5 INVERSES BY ELEMENTARY ROW TRANSFORMATIONS

A system of equations can be modified using the following three steps without changing its solution:

1. The multiplication of every element in any row by a nonzero scalar. This is simply scaling the equation. Thus, if the original equation is 2x = 4 and this equation is scaled by three the resultant equation 6x = 12 still as the same solution of x = 2.
2. The addition (or subtraction) of the elements in any row to the elements of any other row.
3. Combinations of 1 and 2.

If elementary row transformations are successively performed on A such that A is transformed into I, and if throughout the procedure the same row transformations are also done to the same rows of the identity matrix I, the I matrix will be transformed into A⁻¹. This procedure is illustrated using the same matrix used to demonstrate the method of adjoints.

Initially, the original matrix and the identity matrix are listed side by side:

With the following three-row transformations performed on A and I, they are transformed into matrices A₁ and I₁, respectively:

1. Multiply row 1 of matrices A and I by 1/a₁₁ or 1/4. Place the results in row 1 of A₁ and I₁, respectively. This converts a₁₁ of matrix A₁ to 1, as shown below.
   
2. Multiply row 1 of matrices A₁ and I₁ by a₂₁ or 3. Subtract the resulting row from row 2 of matrices A and I and place the difference in row 2 of A₁ and I₁, respectively. This converts a₂₁ of A₁ to zero.
3. Multiply row 1 of matrices A₁ and I₁ by a₃₁ or 2. Subtract the resulting row from row 3 of matrices A and I and place the difference in row 3 of A₁ and I₁, respectively. This changes a₃₁ of A₁ to zero.

After doing these operations, the transformed matrices A₁ and I₁ are

Notice that the first column of A₁ is equivalent to the first column of a 3 × 3 identity matrix as a result of these three-row transformations. For matrices having more than three rows, this same general procedure would be followed for each row to convert the first element in each row of A₁ to zero, with the exception of the first row of A.

Next, the following three elementary row transformations are done on matrices A₁ and I₁ to transform them into matrices A₂ and I₂:

1. Multiply row 2 of A₁ and I₁ by 1/a₂₂ or 4/7 and place the results in row 2 of A₂ and I₂. This converts a₂₂ to 1, as shown below.
   
2. Multiply row 2 of A₂ and I₂ by a₁₂ or 3/4. Subtract the resulting row from row 1 of A₁ and I₁ and place the difference in row 1 of A₂ and I₂, respectively.
3. Multiply row 2 of A₂ and I₂ by a₃₂, which is 3/2. Subtract the resulting row from row 3 of A₁ and I₁ and place the difference in row 3 of A₂ and I₂, respectively.

After doing these operations, the transformed matrices A₂ and I₂ are:

Notice that after this second series of steps is completed, the second column of A₂ conforms to column two of a 3 × 3 identity matrix. Again, for matrices having more than three rows, this same general procedure would be followed for each row, to convert the second element in each row (except the second row) of A₂ to zero.

Finally, the following three-row transformations are applied to matrices A₂ and I₂ to transform them into matrices A₃ and I₃.

1. Multiply row 3 of A₂ and I₂ by 1/a₃₃ or 7/24 and place the results in row 3 of A₃ and I₃, respectively. This converts a₃₃ to 1, as shown below.
   
2. Multiply row 3 of A₂ and I₂ by a₁₃ or 5/7. Subtract the results from row 1 of A₂ and I₂ and place the difference in row 1 of A₃ and I₃, respectively.
3. Multiply row 3 of A₂ and I₂ by a₂₃ or −2/7. Subtract the results from row 2 of A₂ and I₂ and place the difference in row 2 of A₃ and I₃.

Following these operations, the transformed matrices A₃ and I₃ are:

Notice that through these nine elementary row transformations, the original A matrix is transformed into the identity matrix and the original identity matrix is transformed into A⁻¹, which can be verified by multiplying it by the A matrix. Also note that A⁻¹ obtained by this method agrees exactly with the inverse obtained by the method of adjoints. This is because any nonsingular matrix has a unique inverse.

It should be obvious that the quantity of work involved in inverting matrices greatly increases with the matrix size, since the number of necessary row transformations is equal to the square of the number of rows or columns. Because of this, it is not considered practical to invert large matrices by hand. This work is more conveniently done with a computer. Since the procedure of elementary row transformations is systematic, it is easily programmed.

REM INVERT A MATRIX
FOR k = 1 TO n
   FOR j = 1 TO n
     IF j<>k THEN A(k,j) = A(k,j)/A(k,k)
   NEXT j
   A(k,k) = 1/A(k,k)
   FOR i = 1 TO n
     IF  i<>k THEN 
       FOR j=1 TO n
         IF j<>k THEN A(i,j) = A(i,j) - A(i,k)*A(k,j)
       NEXT j
       A(i,k) = -A(i,k)*A(k,k)
     END IF
  NEXT i: NEXT k

      Do 560 k = 1,N
       Do 520 j = 1,N
         If (j.NE.k) Then
             A(k,j) = A(k,j)/A(k,k)
520   Continue
      A(K,K) = 1.0/A(K,K)
      Do 560 i = 1,N
        If (i.EQ.k) Then GOTO 560
          Do 550 j = 1,N
            If (j.NE.k) Then 
              A(i,j) = A(i,j) - A(i,k)*A(k,j)
550   Continue
      A(i,k) = -A(i,k) * A(k,k)
560   Continue

for (k=0; k<n; k++) {
  for (j=0; j<n; j++)
    if (j!=k) A[k][j] = A[k][j]/A[k][k];
  A[k][k] = 1.0/A[k][k];
  for (i=0; i<n; i++)
    if (i!=k) {
      for (j=0; j<n; j++)
        if (j!=k) A[i][j] = A[i][j] - A[i][k]*A[k][j];
      A[i][k] = -A[i][k]*A[k][k];
     } //if i<>k
 } //for k

For k := 1 to N do Begin
  For j := 1 to N do
     If (j<>k) then A[k,j] := A[k,j]/A[k,k];
  A[k,k] := 1.0/A[k,k];
  For i := 1 to N do
    If (i<>k) then Begin
      For j := 1 to N do
        If (j<>k) then A[i,j] := A[i,j] - A[i,k]*A[k,j];
      A[i,k] := -A[i,k]*A[k,k];
    End; { If i<>k }
End; { for k }

Table B.1 shows algorithms, written in BASIC, C, FORTRAN, and Pascal programming languages, for calculating the inverse of any n × n nonsingular matrix A. Students should review the code in their preferred language to gain familiarity with the computer procedures.

B.6 EXAMPLE PROBLEM

PROBLEMS

1. B.1 Explain when a 2 × 2 matrix has no inverse.
2. B.2 Find the inverse of A using the method of adjoints
   
3. B.3 Find the inverse of A in Problem B.2 using elementary row transformations.
4. B.4 Solve the following system of linear equations using matrix methods.
   
5. B.5 Solve the following system of linear equations using matrix methods.
   
6. B.6 Compute the inverses of the following matrices.
   
7. B.7 Compute the inverses of the following matrices.
   
8. B.8 Compute the inverses of the following matrices.
   
9. B.9 Solve the following matrix system.
   

   Use the MATRIX software to do each problem.

10. B.10 Problem B.4.
11. B.11 Problem B.5.
12. B.12 Problem B.6.
13. B.13 Problem B.7.
14. B.14 Problem B.8.
15. B.15 Problem B.9.

PROGRAMMING PROBLEMS

1. B.16 Select one of the coded matrix inverse routines from Table B.1, enter the code into a computer and use it to solve Problem B.7. (Hint: Place the code in Table B.1 in a separate subroutine/function/procedure to be called from the main program.)
2. B.17 Add a block of code to the inverse routine in the language of your choice that will inform the user when a matrix is singular.
3. B.18 Write a program that reads and writes a file with a nonsingular matrix; finds its inverse, and writes the results. Use this program to solve Problem B.7. (Hint: Place the reading, writing, and inversing code in separate subroutines/functions/procedures to be called from the main program. Provide a way to identify each matrix in the output file.)
4. B.19 Write a program that reads and writes a file containing a system of equations written in matrix form, solves the system using matrix operations, and writes the solution. Use this program to solve Problem B.9. (Hint: Place the reading, writing, and inversing code in separate subroutines/functions/procedures to be called from the main program. Provide a way to identify each matrix in the output file.)