In the preceding section, we discussed the case when we have uniform priors. As we saw, in the case of uniform priors, the estimator is not very different from the maximum likelihood estimator. Therefore, in this section, we will move on to discuss the case when we have a non-uniform prior. We will show an example over our coin tossing example, using our prior to be a Beta distribution.

A Beta distribution is defined in the following way:

Here, and are the parameters, and the constant, , is a normalizing constant, which is defined as follows:

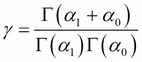
Here, the gamma function, , is defined as follows:

For now, before we start our observations, let's consider that the hyper parameters, and , correspond to the imaginary number of tails and heads. To make our statement more concrete, let's consider the example of a single coin toss and assume that our distribution, . Now, let's try to compute the marginal probability:

So, this conclusion shows that our statement about the hyper parameters is correct. Now, extending this computation for the case when we saw M[1] heads and M[0] tails, we get the following equation:

This equation shows that if the prior distribution is a Beta distribution, the posterior distribution also turns out to be a Beta distribution. Now, using these properties, we can easily compute the probability over the next toss:

Here, , and this posterior represents that we have already seen heads and tails.

Again, let's take our simple example of the network, , and our training data, . We also have unknown parameters, and . We can think of a dependency network over the parameters and data, as shown in Fig 5.2.

This dependency structure gives us a lot of information about datasets and our parameters. We can easily see from the network that different data instances are independent of each other if the parameters are given. So, and are d-separated from and when and are given.

Also, when all the and values are observed, the parameters, and , are d-separated. We can very easily prove this statement, as any path between and is in the following form:

When and are observed, influence cannot flow between and . So, if these two parameters are independent a priori then they will also be independent a posteriori. This d-separation condition leads us to the following result:

This condition is similar to what we saw in the case of the maximum likelihood estimation. This will allow us to break up the estimation problem into smaller and simpler problems, as shown in the following figure:

Fig 5.2: Network structure of data samples and parameters of the network

Now, using the preceding results, let's formalize our problem and see how the results help us solve it. So, we are provided with a network structure, G, whose parameters are . We need to assign a prior distribution over the network parameters, . We define the posterior distribution over these parameters as follows:

Here, the term, , is our prior distribution, is the likelihood function, is our posterior distribution, and P(D) is the normalizing constant.

As we had discussed earlier, we can split our likelihood function as follows:

Also, let's consider that our parameters are independent:

Combining these two equations, we get the following equation:

In the preceding equation, we can see that each of the product terms is for a local parameter value. With this result, let's now try to find the probability of a new data instance given our previous observations:

As we saw earlier, all the data instances are independent. If the parameter is given, we get the following equation:

We can also decompose the posterior probability as follows:

Now, using this equation, we can solve the prediction problem for each of the variables separately.

Now, let's see some examples of the network's learning parameters using this Bayesian approach on the late-for-school model:

In [1]: import numpy as np
In [2]: import pandas as pd
In [3]: from pgmpy.models import BayesianModel
In [4]: from pgmpy.estimators import BayesianEstimator

# Generating some random data
In [5]: raw_data = np.random.randint(low=0, high=2, 

                                     size=(1000, 6))
In [6]: print(raw_data)
Out[6]:
array([[1, 0, 1, 1, 1, 0],
       [1, 0, 1, 1, 1, 1],
       [0, 1, 0, 0, 1, 1],
       ..., 
       [1, 1, 1, 0, 1, 0],
       [0, 0, 1, 1, 0, 1],
       [1, 1, 0, 0, 1, 1]])
In [7]: data = pd.DataFrame(raw_data, columns=['A', 'R', 'J',
                                               'G', 'L', 'Q'])

# Creating the network structures
In [8]: student_model = BayesianModel([('A', 'J'), ('R', 'J'),
                                       ('J', 'Q'), ('J', 'L'), 

                                       ('G', 'L')])
In [9]: student_model.fit(data, estimator=BayesianEstimator)
In [10]: student_model.get_cpds()
Out[10]:
[<TabularCPD representing P(A: 2) at 0x7f92892304fa>,
 <TabularCPD representing P(R: 2) at 0x7f9286c9323b>,
 <TabularCPD representing P(G: 2) at 0x7f9436c9833b>,
 <TabularCPD representing P(J: 2 | A: 2, R: 2) at 0x7f9286s23a34>,
 <TabularCPD representing P(L: 2 | J: 2, G: 2) at
                                            
0x7f9286a932b30>,
 <TabularCPD representing P(Q: 2 | J: 2) at 0x7f9286d12904>]

In [11]: print(student_model.get_cpds('D'))
Out[11]:
╒═════╤═════╕

╘═════╧═════╛
╒═════╤═════╕
│ D_0 │ 0.44│
├─────┼─────┤
│ D_1 │ 0.56│
╘═════╧═════╛

Therefore, to learn the data using the Bayesian approach, we just need to pass the estimator type BayesianEstimator.