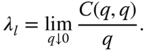Chapter 4
Multivariate Data Analysis
Multivariate data analysis studies simultaneously several time series, but the time series properties are ignored, and thus the analysis can be called cross-sectional.
The copula is an important concept of multivariate data analysis. Copula models are a convenient way to separate multivariate analysis to the purely univariate and to the purely multivariate components. We compose a multivariate distribution into the part that describes the dependence and into the parts that describe the marginal distributions. The marginal distributions can be estimated efficiently using nonparametric methods, but it can be useful to apply parametric models to estimate dependence, for a high-dimensional distribution. Combining nonparametric estimators of marginals and a parametric estimator of the copula leads to a semiparametric estimator of the distribution.
Multivariate data can be described using such statistics as linear correlation, Spearman's rank correlation, and Kendall's rank correlation. Linear correlation is used in the Markowitz portfolio selection. Rank correlations are more natural concepts to describe dependence, because they are determined by the copula, whereas linear correlation is affected by marginal distributions. Coefficients of tail dependence can capture whether the dependence of asset returns is larger during the periods of high volatility.
Multivariate graphical tools include scatter plots, which can be combined with multidimensional scaling and other dimension reduction methods.
Section 4.1 studies measures of dependence. Section 4.2 considers multivariate graphical tools. Section 4.3 defines multivariate parametric distributions such as multivariate normal, multivariate Student, and elliptical distributions. Section 4.4 defines copulas and models for copulas.
4.1 Measures of Dependence
Random vectors 
are said to be independent if
for all measurable 
. This is equivalent to
for all measurable 
, so knowledge of 
does not affect the probability evaluations of 
. The complete dependence between random vectors 
and 
occurs when there is a bijection 
so that
holds almost everywhere. When the random vectors are not independent and not completely dependent we may try to quantify the dependency between two random vectors. We may say that two random vectors have the same dependency when they have the same copula, and the copula is defined in Section 4.4.
Correlation coefficients are defined between two real valued random variables. We define three correlation coefficients: linear correlation 
, Spearman's rank correlation 
, and Kendall's rank correlation 
. All of these correlation coefficients satisfy
where 
and 
are real valued random variables. Furthermore, if 
and 
are independent, then 
for any of the correlation coefficients. Converse does not hold, so that correlation zero does not imply independence.
Complete dependence was defined by (4.1). Both for the Spearman's rank correlation and for the Kendall's rank correlation we have that
where 
or 
. In the case of real valued random variables the complete dependency can be divided into comonotonicity and countermonotonicity. Real-valued random variables 
and 
are said to be comonotonic if there is a strictly increasing function 
so that 
almost everywhere. Real-valued random variables 
and 
are said to be countermonotonic if there is a strictly decreasing function 
so that 
almost everywhere. Both for the Spearman's rank correlation and for the Kendall's rank correlation we have that 
if and only if 
and 
are comonotonic, and 
if and only if 
and 
are countermonotonic, where 
or 
.
The linear correlation coefficient 
does not satisfy (4.2). However, we have that
If 
, then 
. If 
, then 
.
4.1.1 Correlation Coefficients
We define linear correlation 
, Spearman's rank correlation 
, and Kendall's rank correlation 
.
4.1.1.1 Linear Correlation
The linear correlation coefficient between real valued random variables 
and 
is defined as
where the covariance is
and the standard deviation is 
.
We noted in (4.3) that the linear correlation coefficient characterizes linear dependency. However, (4.2) does not hold for the linear correlation coefficient. Even when 
and 
are completely dependent, it can happen that 
. For example, let 
, 
, and 
, where 
. Then,
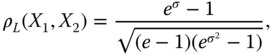
and 
only for 
, otherwise 
; the example is from McNeil et al. (2005, p. 205).
Let us assume that 
and 
have continuous distributions and let us denote with 
the distribution function of 
and with 
and 
the marginal distribution functions. Then,
where 
, 
, is the copula of the distribution of 
, as defined in (4.29). Equation (4.5) is called Höffding's formula, and its proof can be found in McNeil et al. (2005, p. 203). Thus, the linear correlation is not solely a function of the copula, it depends also on the marginal distributions 
and 
.
The linear correlation coefficient can be estimated with the sample correlation. Let 
be a sample from the distribution of 
and 
be a sample from the distribution of 
. The sample correlation coefficient is defined as
where 
and 
. An alternative estimator is defined in (4.10).
4.1.1.2 Spearman's Rank Correlation
Spearman's rank correlation (Spearman's rho) is defined by
where 
is the distribution function of 
, 
. If 
and 
have continuous distributions, then
where 
, 
, is the copula as defined in Section 4.4 (see McNeil et al., 2005, p. 207).1 Thus, Spearman's correlation coefficient is defined solely in terms of the copula.
We have still another way of writing Spearman's rank correlation. Let 
, 
, and 
, let 
have the same distribution, and let 
be independent. Then,
The sample Spearman's rank correlation can be defined as the sample linear correlation coefficient between the ranks. Let 
be a sample from the distribution of 
and 
be a sample from the distribution of 
. The rank of observation 
, 
, 
, is
That is, 
is the number of observations of the 
th variable smaller or equal to 
.2
Let us use the shorthand notation
so that 
, 
. Then the sample Spearman's rank correlation can be written as
where 
is the sample linear correlation coefficient, defined in (4.6). Since 
and 
, we can write
4.1.1.3 Kendall's Rank Correlation
Let 
and 
, let 
and 
have the same distribution, and let 
and 
be independent. Kendall's rank correlation (Kenadall's tau) is defined by
When 
and 
have continuous distributions, we have
and we can write
where 
, 
, is the copula as defined in Section 4.4 (see McNeil et al., 2005, p. 207).
Let us define an estimator for 
. Let 
be a sample from the distribution of 
and 
be a sample from the distribution of 
. Kendall's rank correlation can be written as
where 
, if 
and 
, if 
. This leads to the sample version
The computation takes longer than for the sample linear correlation and for the sample Spearman's correlation.
4.1.1.4 Relations between the Correlation Coefficients
We have a relation between the linear correlation and the Kendall's rank correlation for the elliptical distributions. Let 
be a bivariate random vector. For all elliptical distributions with 
,
where 
is the Kendall's rank correlation, as defined in (4.7), and 
is the linear correlation, as defined in (4.4) (see McNeil et al., 2005, p. 217). This relationship can be applied to get an alternative and a more robust estimator for the estimator (4.6) of linear correlation. Define the estimator as
where 
is the estimator (4.8).
For the distributions with a Gaussian copula, we also have a relation between the Spearman's rank correlation and the linear correlation. Let 
be a distribution with a Gaussian copula and continuous margins. Then,
and (4.9) holds also (see McNeil et al., 2005, p. 215).
Figure 4.1 studies linear correlation and Spearman's rank correlation for S&P 500 and Nasdaq-100 daily data, described in Section 2.4.2. Panel (a) shows a moving average estimate of linear correlation (blue) and Spearman's rank correlation (yellow). We use the one-sided moving average defined as
where 
are the S&P 500 centered returns and 
are the Nasdaq-100 centered returns. The weights 
are one for the last 500 observations, and zero for the other observations. See (6.5) for a more general moving average. The moving average estimator 
is the Spearman's rho computed from the 500 previous observations. Panel (b) shows the correlation coefficients together with the moving average estimates of the standard deviation of S&P 500 returns (solid black line) and Nasdaq-100 returns (dashed black line). All time series are scaled to take values in the interval 
. We see that there is some tendency that the inter-stock correlations increase in volatile periods.
Figure 4.1 Linear and Spearman's correlation, together with volatility. (a) Time series of moving average estimates of correlation between S&P 500 and Nasdaq-100 returns, with linear correlation (blue) and Spearman's rho (yellow); (b) we have added moving average estimates of the standard deviation of S&P 500 (black solid) and Nasdaq-100 (black dashed).
4.1.2 Coefficients of Tail Dependence
The coefficient of upper tail dependence is defined for random variables 
and 
with distribution functions 
and 
as
where 
and 
are the generalized inverses. Similarly, the coefficient of lower tail dependence is
See McNeil et al. (2005, p. 209).
4.1.2.1 Tail Coefficients in Terms of the Copula
The coefficients of upper and lower tail dependence can be defined in terms of the copula. Let 
and 
be continuous. We have that
Also,
Thus, the coefficient of upper tail dependence is
We have that
Also,
Thus, the coefficient of lower tail dependence for continuous 
and 
is equal to
4.1.2.2 Estimation of Tail Coefficients
Equations (4.11) and (4.12) suggest estimators for the coefficients of tail dependence. We can estimate the upper tail coefficient nonparametrically, using
where 
is the empirical copula, defined in (4.38), and 
is close to 1. We can take, for example, 
, where 
. The coefficient of lower tail dependence can be estimated by
where 
is close to zero. We can take, for example, 
, where 
. These estimators have been studied in Dobric and Schmid (2005), Frahm et al. (2005), and Schmidt and Stadtmüller (2006).
Figure 4.2 studies tail coefficients for S&P 500 and Nasdaq-100 daily data, described in Section 2.4.2. Panel (a) shows the tail coefficients as a function of 
for lower tail coefficients (red) and as a function of 
for upper tail coefficients (blue). Panel (b) shows a moving average estimate of the lower tail coefficients. The tail coefficient is estimated using the window of the latest 1000 observations, for 
.
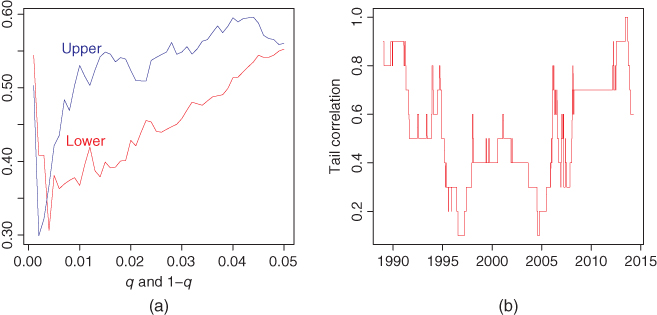
Figure 4.2 Tail coefficients for S&P 500 and Nasdaq-100 returns. (a) Tail coefficients as a function of 
for lower tail coefficients (red) and as a function of 
for upper tail coefficients (blue); (b) time series of moving average estimates of lower tail coefficients.
4.1.2.3 Tail Coefficients for Parametric Families
The coefficients of lower and upper tail dependence for the Gaussian distributions are zero. The coefficients of lower and upper tail dependence for the Student distributions with degrees of freedom 
and correlation coefficient 
are
where 
is the distribution function of the univariate 
-distribution with 
degrees of freedom, and we assume that 
; see McNeil et al. (2005, p. 211).
4.2 Multivariate Graphical Tools
First, we describe scatter plots and smooth scatter plots. Second, we describe visualization of correlation matrices with multidimensional scaling.
4.2.1 Scatter Plots
A two-dimensional scatter plot is a plot of points 
.
Figure 4.3 shows scatter plots of daily net returns of S&P 500 and Nasdaq-100. The data is described in Section 2.4.2. Panel (a) shows the original data and panel (b) shows the corresponding scatter plot after copula preserving transform with standard normal marginals, as defined in (4.36).
Figure 4.3 Scatter plots. Scatter plots of the net returns of S&P 500 and Nasdaq-100. (a) Original data; (b) copula transformed data with marginals being standard normal.
When the sample size is large, then the scatter plot is mostly black, so the visuality of density of the points in different regions is obscured. In this case it is possible to use histograms to obtain a smooth scatter plot. A multivariate histogram is defined in (3.42). First we take square roots 
of the bin counts 
and then we define 
. Now 
. Values 
close to one are shown in light gray, and values 
close to zero are shown in dark gray. See Carr et al. (1987) for a study of histogram plotting.
Figure 4.4 shows smooth scatter plots of daily net returns of S&P 500 and Nasdaq-100. The data is described in Section 2.4.2. Panel (a) shows a smooth scatter plot of the original data and panel (b) shows the corresponding scatter plot after copula preserving transform when the marginals are standard Gaussian.
Figure 4.4 Smooth scatter plots. Scatter plots of the net returns of S&P 500 and Nasdaq-100. (a) Original data; (b) copula transformed data with marginals being standard normal.
4.2.2 Correlation Matrix: Multidimensional Scaling
First, we define the correlation matrix. Second, we show how the correlation matrix may be visualized using multidimensional scaling.
4.2.2.1 Correlation Matrix
The correlation matrix is the 
matrix whose elements are the linear correlation coefficients 
for 
. The sample correlation matrix is the matrix whose elements are the sample linear correlation coefficients.
The correlation matrix can be defined using matrix notation. The covariance matrix of random vector 
is defined by
The covariance matrix is the 
matrix whose elements are 
for 
, where we denote 
. Let
be the diagonal matrix whose diagonal is the vector of the inverses of the standard deviations. Then the correlation matrix is
The covariance matrix can be estimated by the sample covariance matrix
where 
are identically distributed observations whose distribution is the same as the distribution of 
, and 
is the arithmetic mean.
4.2.2.2 Multidimensional Scaling
Multidimensional scaling makes a nonlinear mapping of data 
to 
, or to any space 
with 
. We can define the mapping 
of multidimensional scaling in two steps:
- 1. Compute the pairwise distances
, 
. - 2. Find points
so that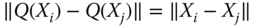 
for 
.
In practice, we may not be able to find a mapping that preserves the distances exactly, but we find a mapping 
so that the stress functional
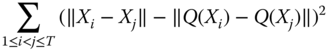
is minimized. Sammon's mapping uses the stress functional
This stress functional emphasizes small distances. Numerical minimization is needed to solve the minimization problems.
Multidimensional scaling can be used to visualize correlations between time series. Let 
be the time series of returns of company 
, where 
. When we normalize the time series of returns so that the vector of returns has sample mean zero and sample variance one, then the Euclidean distance is equivalent to using the correlation distance. Indeed, let
where 
and 
. Now
where 
is the sample linear correlation. Thus, we apply the multidimensional scaling for the norm
which is obtained by dividing the Euclidean norm by 
. Since
we have that
Zero correlation gives 
, positive correlations give 
, and negative correlations give 
.
Figure 4.5 studies correlations of the returns of the components of DAX 30. We have daily observations of the components of DAX 30 starting at January 02, 2003 and ending at May 20, 2014, which makes 2892 observations. Panel (a) shows the correlation matrix as an image. We have used R-function “image.” Panel (b) shows the correlations with multidimensional scaling. We have used R-function “cmdscale.” The image of the correlation matrix is not as helpful as the multidimensional scaling. For example, we see that the return time series of Volkswagen with the ticker symbol “VOW” is an outlier. The returns of Fresenius and Fresenius Medical Care (“FRE” and “FME”) are highly correlated.
Figure 4.5 Correlations of DAX 30. (a) An image of the correlation matrix for DAX 30; (b) correlations for DAX 30 with multidimensional scaling.
4.3 Multivariate Parametric Models
We give examples of multivariate parametric models. The examples include Gaussian and Student distributions (
-distributions). More general families are normal variance mixture distributions and elliptical distributions.
4.3.1 Multivariate Gaussian Distributions
A 
-dimensional Gaussian distribution can be parametrized with the expectation vector 
and the 
covariance matrix 
. When random vector 
follows the Gaussian distribution with parameters 
and 
, then we write 
or 
. We say that a Gaussian distribution is the standard Gaussian distribution when 
and 
. The density function of the Gaussian distribution is
where 
and 
is the determinant of 
. The characteristic function of the Gaussian distribution is
where 
.
A linear transformation of a Gaussian random vector follows a Gaussian distribution: When 
, 
is 
matrix, and 
is a 
vector, then
Also, when 
and 
are independent, then
Both of these facts can be proved using the characteristic function.3
4.3.2 Multivariate Student Distributions
A 
-dimensional Student distribution (
-distribution) is parametrized with degrees of freedom 
, the expectation vector 
, and the 
positive definite symmetric matrix 
. When random vector 
follows the 
-distribution with parameters 
, 
, and 
, then we write 
or 
. The density function of the multivariate 
-distribution is
where
The multivariate Student distributed random vector has the covariance matrix
when 
.
When 
, then the Student density approaches a Gaussian density. Indeed, 
, as 
, since 
, when 
. The Student density has tails 
, as 
.
Figure 4.6 compares multivariate Gaussian and Student densities. Panel (a) shows the Gaussian density with marginal standard deviations equal to one and correlation 0.5. Panel (b) shows the density of 
-distribution with degrees of freedom 2 and correlation 0.5. The density contours are in both cases ellipses but the Student density has heavier tails.
Figure 4.6 Gaussian and Student densities. (a) Contour plot of the Gaussian density with marginal standard deviations equal to one and correlation 0.5; (b) Student density with degrees of freedom 2 and correlation 0.5.
4.3.3 Normal Variance Mixture Distributions
Random vector 
follows a Gaussian distribution with parameters 
and 
when 
for a 
matrix 
and
where 
follows the standard Gaussian distribution. This leads to the definition of a normal variance mixture distribution. We say that 
follows a normal variance mixture distribution when
where 
follows the standard Gaussian distribution, and 
is a random variable independent of 
. It holds that
and
where 
. When random vector 
follows the normal variance mixture distribution with parameters 
, 
, and 
, where 
is the distribution function on 
, then we write 
.
The density function can be calculated as
where 
is the density of 
, 
is the density of 
, 
is the density of 
conditional on 
, and 
is defined by
The characteristic function is obtained, using (4.16), as
where 
.
The family of normal variance mixtures 
is closed under linear transformations: When 
, 
is 
matrix, and 
is a 
vector, then
This can be seen using the characteristic function, similarly as in (4.17).
Let 
be such random variable that 
follows the 
-distribution with degrees of freedom 
. Then the normal variance mixture distribution is the multivariate 
-distribution 
, where 
, as defined in Section 4.3.2.
4.3.4 Elliptical Distributions
The density function of an elliptical distribution has the form
where 
is called the density generator, 
is a symmetric positive definite 
matrix, and 
. Since 
is positive definite, it has inverse 
that is positive definite, which means that for all 
, 
. Thus, 
needs to be defined only on the nonnegative real axis. Let 
be such that 
. Then 
is a density generator when 
is chosen by
where 
. We give examples of density generators.
- 1. From (4.15) we see that the Gaussian distributions are elliptical and the Gaussian density generator is
4.25
- where
. - 2. From (4.20) we see that the normal variance mixture distributions are elliptical and the normal variance mixture density generator is given in (4.21).
- 3. From (4.18) we see that the
-distributions are elliptical and the Student density generator is
4.26
- where
is the degrees of freedom, and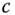 
is defined in (4.19). The Student density generator has tails 
, as 
, and thus the density function is integrable when 
, according to (4.24).
Let 
, where 
is a 
matrix and let
where 
follows a spherical distribution with density 
. Then 
follows an elliptical distribution with density (4.23). When random vector 
follows the elliptical distribution with parameters 
, 
, and 
, where 
is the distribution function on 
, then we write 
. The family of elliptical distributions is closed under linear transformations: When 
, 
is a 
matrix, and 
is a 
vector, then
This can be seen using the characteristic function, similarly as in (4.17).
4.4 Copulas
We can decompose a multivariate distribution into a part that describes the dependence and into parts that describe the marginal distributions. This decomposition helps to estimate and analyze multivariate distributions, and it helps to construct new parametric and semiparametric models for multivariate distributions.
The distribution function 
of random vector 
is defined by
where 
. The distribution functions 
, …, 
of the marginal distributions are defined by
where 
.
A copula is a distribution function 
whose marginal distributions are the uniform distributions on 
. Often it is convenient to define a copula as a distribution function 
whose marginal distributions are the standard normal distributions. Any distribution function 
may be written as
where 
, 
, are the marginal distribution functions and 
is a copula. In this sense we can decompose a distribution into a part that describes only the dependence and into parts that describe the marginal distributions.
We show in (4.29) how to construct a copula of a multivariate distribution and in (4.31) how to construct a multivariate distribution function from a copula and marginal distribution functions. We restrict ourselves to the case of continuous marginal distribution functions. These constructions were given in Sklar (1959), who considered also the case of noncontinuous margins. For notational convenience we give the formulas for the case 
. The generalization to the cases 
is straightforward.
4.4.1 Standard Copulas
We use the term “standard copula,” when the marginals of the copula have the uniform distributions on 
. Otherwise, we use the term “nonstandard copula.”
4.4.1.1 Finding the Copula of a Multivariate Distribution
Let 
and 
be real valued random variables with distribution functions 
and 
. Let 
be the distribution function of 
, and assume that 
and 
are continuous. Then,
where
and 
. We call 
in (4.29) the copula of the joint distribution of 
and 
. Copula 
is the distribution function of the vector 
, 
, and 
and 
are uniformly distributed random variables.4
The copula density is
because 
, where 
is the density of 
and 
and 
are the densities of 
and 
, respectively.
4.4.1.2 Constructing a Multivariate Distribution from a Copula
Let 
be a copula, that is, it is a distribution function whose marginal distributions are uniform on 
. Let 
and 
be univariate distribution functions of continuous distributions. Define 
by
Then 
is a distribution function whose marginal distributions are given by distribution functions 
and 
. Indeed, Let 
be a random vector with distribution function 
. Then,
and 
for 
, because 
.5
4.4.2 Nonstandard Copulas
Typically a copula is defined as a distribution function with uniform marginals. However, we can define a copula so that the marginal distributions of the copula is some other continuous distribution than the uniform distribution on 
. It turns out that we get simpler copulas by choosing the marginal distributions of a copula to be the standard Gaussian distribution.
As in (4.28) we can write distribution function 
as
where 
is the distribution function of the standard Gaussian distribution and
. Now 
is a distribution function whose marginals are standard Gaussians, because 
follow the uniform distribution on 
and thus 
follow the standard Gaussian distribution.
Conversely, given a distribution function 
with the standard Gaussian marginals, and univariate distribution functions 
and 
, we can define a distribution function 
with marginals 
and 
by the formula
The copula density is
where 
is the density of 
, 
and 
are the densities of 
and 
, respectively, and 
is the density of the standard Gaussian distribution.
4.4.3 Sampling from a Copula
We do not have observations directly from the distribution of the copula but we show how to transform the sample so that we get a pseudo sample from the copula. Scatter plots of the pseudo sample can be used to visualize the copula. The pseudo sample can also be used in the maximum likelihood estimation of the copula. Before defining the pseudo sample, we show how to generate random variables from a copula.
4.4.3.1 Simulation from a Copula
Let random vector 
have a continuous distribution. Let 
, 
, be the distribution functions of the margins of 
. Now
is a random vector whose marginal distributions are uniform on 
. The distribution function of this random vector is the copula of the distribution of 
. Thus, if we can generate a random vector 
with distribution 
, we can use the rule (4.34) to generate a random vector 
whose distribution is the copula of 
. Often the copula with uniform marginals is inconvenient due to boundary effects. We may get statistically more tractable distribution by defining
where 
is the distribution function of the standard Gaussian distribution. The components of 
have the standard Gaussian distribution.
4.4.3.2 Transforming the Sample
Let us have data 
and denote 
. Let the rank of observation 
, 
, 
, be
That is, 
is the number of observations of the 
th variable smaller or equal to 
. We normalize the ranks to get observations on 
:
for 
. Now 
for 
. In this sense we can consider the observations as a sample from a distribution whose margins are uniform distributions on 
. Often the standard Gaussian distribution is more convenient and we define
for 
.
4.4.3.3 Transforming the Sample by Estimating the Margins
We can transform the data 
using estimates of the marginal distributions. Let 
and 
be estimates of the marginal distribution functions 
and 
, respectively. We define the pseudo sample as
where 
. The estimates 
and 
can be parametric estimates. For example, assuming that the 
th marginal distribution is a normal distribution, we would take 
, where 
is the distribution function of the standard normal distribution, 
is the sample mean of 
, and 
is the sample standard deviation. If 
are the empirical distribution functions
then we get almost the same transformation as (4.35), but 
is now replaced by 
:
4.4.3.4 Empirical Copula
The empirical distribution function 
is calculated using a sample 
of identically distributed observations, and we define
where we denote 
.
The empirical copula is defined similarly as the empirical distribution function. Now,
where 
are defined in (4.37).
4.4.3.5 Maximum Likelihood Estimation
Pseudo samples are needed in maximum likelihood estimation. In maximum likelihood estimation we assume that the copula has a parametric form. For example, the copula of the normal distribution, given in (4.39), is parametrized with the correlation matrix, which contains 
parameters. Let 
be the copula with parameter 
. The corresponding copula density is 
, as given in (4.30). Let us have independent and identically distributed observations 
from the distribution of 
. We calculate the pseudo sample 
using (4.35) or (4.37). A maximum likelihood estimate is a value 
maximizing
over 
.
4.4.4 Examples of Copulas
We give examples of parametric families of copulas. The examples include the Gaussian copulas and the Student copulas.
4.4.4.1 The Gaussian Copulas
Let 
be a 
-dimensional Gaussian random vector, as defined in Section 4.3.1. The copula of 
is
where 
is the distribution function of 
distribution, 
is the correlation matrix of 
, and 
is the distribution function of 
distribution.
Indeed, let us denote 
, where 
is the standard deviation of 
. Then 
follows the distribution 
.6 Let 
be the distribution function of 
. Then, using the notation 
,
where 
. Also,7
for 
. Thus,
Figure 4.7 shows perspective plots of the densities of the Gaussian copula. The margins are uniform on 
. The correlation parameter is in panel (a) 
and in panel (b) 
. Figure 4.7 shows that the perspective plots of the copula densities are not intuitive, because the probability mass is concentrated near the corners of the square 
, especially when the correlation is high. From now on we will show only pictures of copulas with standard Gaussian margins, as defined in (4.32), because these give more intuitive representation of the copula.
Figure 4.7 Gaussian copulas. Perspective plots of the densities of the Gaussian copula with the correlation (a) 
and (b) 
. The margins are uniform on 
.
4.4.4.2 The Student Copulas
Let 
be a 
-dimensional 
-distributed random vector, as defined in Section 4.3.2. The copula of 
is
where 
is the distribution function of 
distribution, 
is the correlation matrix of 
, and 
is the distribution function of the univariate 
-distribution with degrees of freedom 
.
Indeed, the claim follows similarly as in the Gaussian case for
where 
and 
is the square root of the 
th element in the diagonal of 
. The matrix 
is indeed the correlation matrix, since
where 
, 
.
Figure 4.8 shows contour plots of the densities of the Student copula when the margins are standard Gaussian. The correlation is 
. The degrees of freedom are in panel (a) two and in panel (b) four. The Gaussian and Student copulas are similar in the main part of the distribution but they differ in the tails (in the corners of the unit square). The Gaussian copula has independent extremes (asymptotic tail independence) but the Student copula generates concomitant extremes with a nonzero probability. The probability of concomitant extremes is larger when the degrees of freedom is smaller and the correlation coefficient is larger.
Figure 4.8 Student copula with standard Gaussian margins. Contour plots of the densities of the Student copula with degrees of freedom (a) 2 and (b) 4. The correlation is 
.
4.4.4.3 Other Copulas
We define Gumbel and Clayton copulas. These are examples of Archimedean copulas. Gaussian and Student copulas are examples of elliptical copulas.
The Gumbel–Hougaard Copulas
The Gumbel–Hougaard or the Gumbel family of copulas is defined by
where 
is the parameter. When 
, then 
and when 
, then 
.
Figure 4.9 shows contour plots of the densities with the Gumbel copula when 
, 
, and 
. The marginals are standard Gaussian.
Figure 4.9 Gumbel copula. Contour plots of the densities of the Gumbel copula with 
, 
, and 
. The marginals are standard Gaussian.
The Clayton Copulas
Clayton's family of copulas is defined by
where 
. When 
, we define 
. When the parameter 
increases, then the dependence between coordinate variables increases. The dependence is larger in the negative orthant. The Clayton family was discussed in Clayton (1978).
Figure 4.10 shows contour plots of the densities with the Clayton copula when 
, 
, and 
. The marginals are standard Gaussian.
Figure 4.10 Clayton copula. Contour plots of the densities of the Clayton copula with 
, 
, and 
. The marginals are standard Gaussian.
Elliptical Copulas
Elliptical distributions are defined in Section 4.3.4. An elliptical copula is obtained from an elliptical distribution 
by the construction (4.29). The Gaussian copula and the Student copula are elliptical copulas.
Archimedean Copulas
Archimedean copulas have the form
where 
is strictly decreasing, continuous, convex, and 
. For 
to be a copula, we need that 
, 
. The function 
is called the generator. The product copula, Gumbel copula, Clayton copula, and Frank copula are all Archimedean copulas and we have:
- product copula:
, - Gumbel copula:
, - Clayton copula:
, - Frank copula:
.
The density of an Archimedean copula is
where 
is the second derivative of 
:
because 
. We have:
- Gumbel copula:
, 
, 
, - Clayton copula:
, 
, 
, - Frank copula:
, 
, 
.
4.4.4.4 Empirical Results
Research on testing the hypothesis of Gaussian copula and other copulas on financial data has been done in Malevergne and Sornette (2003), and summarized in Malevergne and Sornette (2005). They found that the Student copula is a good model for foreign exchange rates but for the stock returns the situation is not clear.
Patton (2005) takes into account the volatility clustering phenomenon. He filters the marginal data by a GARCH process and shows that the conditional dependence structure between Japanese Yen and Euro is better described by Clayton's copula than by the Gaussian copula. Note, however, that the copula of the residuals is not the same as the copula of the raw returns and many filters can be used (ARCH, GARCH, and multifractal random walk). Using the multivariate multifractal filter of Muzy et al. (2001) leads to a nearly Gaussian copula.
Breymann et al. (2003) show that the daily returns of German Mark/Japanese Yen are best described by a Student copula with about six degrees of freedom, when the alternatives are the Gaussian, Clayton's, Gumbel's, and Frank's copulas. The Student copula seems to provide an even better description for returns at smaller time scales, when the time scale is larger than 2 h. The best degrees of freedom is four for the 2-h scale.
Mashal and Zeevi (2002) claim that the dependence between stocks is better described by a Student copula with 11–12 degrees of freedom than by a Gaussian copula.
where 
is the characteristic function of 
.