Chapter 2
Financial Instruments
The basic assets which are traded in financial markets include stocks and bonds. A large part of financial markets consists of trading with derivative assets, like futures and options, whose prices are derived from the prices of the basic assets. Stock indexes can be considered as derivative assets, since the price of a stock index is a linear combination of the prices of the underlying stocks. A stock index is a more simple derivative asset than an option, whose terminal price is a nonlinear function of the price of the underlying stock.
In addition, we describe in this section the data sets which are used throughout the book to illustrate the methods.
2.1 Stocks
Stocks are securities representing an ownership in a corporation. The owner of a stock has a limited liability. The limited liability implies that the price of a stock is always nonnegative, so that the price ![]() of a stock at time
of a stock at time ![]() satisfies
satisfies
Stock issuing companies have a variety of legal forms depending on the country of domicile of the company.1 Common stock typically gives voting rights in company decisions, whereas preferred stock does not typically give voting rights, but the owners of preferred stocks are entitled to receive a certain amount of dividend payments before the owners of common stock can receive any dividends.
2.1.1 Stock Indexes
We define a stock index, give examples of the uses of stock indexes, and give examples of popular stock indexes.
2.1.1.1 Definition of a Stock Index
The price of a stock index is a weighted sum of stock prices. The value ![]() of a stock index at time
of a stock index at time ![]() is calculated by formula
is calculated by formula
where ![]() is a constant,
is a constant, ![]() is the number of stocks in the index,
is the number of stocks in the index, ![]() is the number of shares of stock
is the number of shares of stock ![]() , and
, and ![]() is a suitably adjusted price of stock
is a suitably adjusted price of stock ![]() at time
at time ![]() , where
, where ![]() . Note that
. Note that ![]() is the market capitalization of stock
is the market capitalization of stock ![]() . The definition of a stock index involves three parameters: constant
. The definition of a stock index involves three parameters: constant ![]() , numbers
, numbers ![]() , and values
, and values ![]() :
:
- 1. The constant
 can be chosen, for example, to make the value of the index equal to 100 at a given past day. When the constitution of the index is changed, then the constant
can be chosen, for example, to make the value of the index equal to 100 at a given past day. When the constitution of the index is changed, then the constant  is changed, to keep the index equal to 100 at the chosen day.
is changed, to keep the index equal to 100 at the chosen day. - 2. The numbers
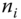 can equal the total number of shares of stock
can equal the total number of shares of stock  , but they can also be equal to the number of freely floating stocks. Float market capitalization excludes stocks which are not freely floating (cannot be bought in the open market).
, but they can also be equal to the number of freely floating stocks. Float market capitalization excludes stocks which are not freely floating (cannot be bought in the open market). - 3. The values
 are calculated differently depending on whether the index is a price return index or a total return index. Price return indexes are calculated without regard to cash dividends but total return indexes are calculated by reinvesting cash dividends. The adjusted closing price of a stock is the closing price of a stock which is adjusted to cash dividends, stock dividends, stock splits, and also to more complex corporate actions, such as rights offerings. The calculation of the adjusted closing price is often made by data providers.
are calculated differently depending on whether the index is a price return index or a total return index. Price return indexes are calculated without regard to cash dividends but total return indexes are calculated by reinvesting cash dividends. The adjusted closing price of a stock is the closing price of a stock which is adjusted to cash dividends, stock dividends, stock splits, and also to more complex corporate actions, such as rights offerings. The calculation of the adjusted closing price is often made by data providers.
2.1.1.2 Uses of Stock Indexes
Stock indexes can be used to summarize information about stock markets. Stock indexes can also be used as a proxy for the market index when testing and applying finance theories. The market index is the stock index which sums the values of all companies worldwide. Stock indexes are traded in futures markets and in exchanges as exchange traded funds (ETF). Furthermore, investment banks provide financial instruments whose values depend on stock indexes.
2.1.1.3 Examples of Stock Indexes
Dow Jones Industrial Average
Dow Jones Industrial Average is an index where the prices are not weighted by the number of shares, and thus Dow Jones Industrial Average is an exception of the rule (2.1). Dow Jones Industrial Average is just a sum of the prices of the components, multiplied by a constant.
S&P 500
S&P 500 was created at March 4, 1957. It was calculated back until 1928 and the basis value was taken to be 10 from 1941 until 1943. The S&P 500 index is a price return index, but there exists also total return versions (dividends are invested back) and net total return versions (dividends minus taxes are invested back) of the S&P 500 index. The S&P 500 is a market value weighted index: prices of stocks are weighted according to the market capitalizations of the companies. Since 2005 the index is float weighted, so that the market capitalization is calculated using only stocks that are available for public trading.
Nasdaq-100
Nasdaq-100 is calculated since January 31, 1985. The basis value was at that day 250. Nasdaq-100 is a price index, so that the dividends are not included in the value of the index. Nasdaq-100 is a different index than Nasdaq Composite, which is based on 3000 companies. Nasdaq-100 is calculated using the 100 largest companies in Nasdaq Composite. Nasdaq-100 is a market value weighted index, but the influence of the largest companies is capped (the weight of any single company is not allowed to be larger than ![]() ).
).
DAX 30
DAX 30 (Deutscher AktienindeX) was created at July 1, 1988. The basis value is 1000 at December 31, 1987. DAX 30 is a performance index (dividends are reinvested in calculating the value of the index). DAX 30 stock index is a market value weighted index of 30 largest German companies. Market value is calculated using only free floating stocks (stocks that are not owned by an owner which has more than ![]() of stocks). The largeness of a company is measured by taking into account both the free floating market value and the transaction volume (total value of the stocks that are exchanged in a given time period). The weight of any single company is not allowed to be larger than
of stocks). The largeness of a company is measured by taking into account both the free floating market value and the transaction volume (total value of the stocks that are exchanged in a given time period). The weight of any single company is not allowed to be larger than ![]() .
.
2.1.2 Stock Prices and Returns
Statistical analysis of stock markets is usually done from time series of returns. Before defining a return time series we describe the initial price data in its raw form, as it is evolving in a stock exchange, and we describe some methods of sampling of prices.
2.1.2.1 Initial Price Data
During the opening hours of an exchange the stocks are changing hands at irregular time points. The stock exchange receives bid prices with volumes (numbers of stocks one is willing to buy with the given bid price) from buyers, and ask prices with volumes from the sellers. The exchange has an algorithm which allocates the stocks from the sellers to the buyers. The allocation happens when there are bid prices and ask prices that meet each other (ask prices that are smaller or equal to bid prices). The algorithms of stock allocation take into account the arrival times of the orders, the volumes of the orders, and the types of the orders.
The most common order types are the market order and the limit order. A market order expresses the intention to buy the stock at the lowest ask price, or the intention to sell the stock at the highest bid price. A limit order expresses the intention to buy the stock at the lowest ask price, under the condition that the ask price is lower than the given limit price, or the intention to sell the stock at the highest bid price, under the condition that the bid price is higher than the given limit price.
2.1.2.2 Sampling of Prices
The price changes at irregular time intervals in a stock exchange, but for the purpose of a statistical analysis we typically sample price at equispaced intervals.
To obtain a time series of daily prices, we can pick the closing price of each trading day. The closing price can be considered as the consensus reached between the sellers and the buyers about the fair price, taking into account all information gathered during the day. An alternative method would choose the opening price.
However, depending on the purpose of the analysis, we can sample data once in a second, once in 10 days, or once in a month, for example. Note that when the sampling interval is longer (monthly, quarterly, or yearly), the number of observations in a return time series will be smaller, and thus the statistical conclusions may be more vague. Note also, that the distribution of the returns may vary depending on the sampling frequency.
It is not obvious how to define equispaced sampling, since we can measure the time as the physical time, trading time, or effective trading time:
- 1. The physical time is the usual time in calendar days. Assume that we want to sample data once in 20 days. If we use the physical time, then we calculate all calendar days.
- 2. The trading time or market time takes into account only the time when markets are open. For example, when we want to sample data once in 20 days and we use trading time, then we calculate only the trading days (not all calendar days). However, information is accumulating also during the weekends (and during the night), which would be an argument in favor of physical time.
- 3. The effective trading time takes into account that the market activity is not uniform during market hours. To define the sampling interval, we could take into account the number of transactions, or the volume of the transactions. The effective trading time is interesting especially when we gather intraday data, but it can be used also in the case of longer sampling intervals, to correct for diminishing market activity during summer or at the end of year.2
Sampling daily closing prices can be interpreted as using the trading time, because weekends and holidays are ignored in the daily sampling. Since there is roughly the same number of trading days in every week and every month, we can interpret sampling the weekly and monthly closing prices both as using the physical time and using the trading time. Discussion about scales in finance is provided by Mantegna and Stanley (2000).
2.1.2.3 Stock Returns
Let us consider a time series ![]() of stock prices, sampled at equispaced time points. We can calculate gross returns, net returns, or logarithmic returns.
of stock prices, sampled at equispaced time points. We can calculate gross returns, net returns, or logarithmic returns.
- 1. Gross returns (price relatives) are defined by

- 2. net returns (relative price differences) are defined by

- 3. logarithmic returns (continuously compounded returns) are defined by

where ![]() .
.
Gross returns are positive numbers like 1.02 (when the stock rose 2%) or 0.98 (when the stock fell 2%). Value zero for a gross return means bankruptcy. The gross returns have a concrete interpretation: starting with wealth ![]() and buying a stock with price
and buying a stock with price ![]() leads to the wealth
leads to the wealth ![]() .
.
Net returns are obtained from gross returns by subtracting one, and thus net returns are numbers larger than ![]() . Net returns are numbers like 0.02 (when the stock rose 2%) or
. Net returns are numbers like 0.02 (when the stock rose 2%) or ![]() (when the stock fell 2%). Value
(when the stock fell 2%). Value ![]() for a net return means bankruptcy.
for a net return means bankruptcy.
Logarithmic returns are obtained from gross returns by taking the logarithm.3 A logarithmic return can take any real value, but typically logarithmic returns are close to net returns, because ![]() when
when ![]() . Value
. Value ![]() for a logarithmic return means bankruptcy. The logarithmic function is an example of a utility function, as discussed in Section 9.2.2. We will consider taking the logarithm as an application of a utility function, and apply mainly gross returns. However, there are some reasons for the use of logarithmic returns. First, we can derive approximate distributions for the stock price by applying limit theorems for the sum of the logarithmic returns, which makes the study of logarithmic returns interesting. Indeed, we can write
for a logarithmic return means bankruptcy. The logarithmic function is an example of a utility function, as discussed in Section 9.2.2. We will consider taking the logarithm as an application of a utility function, and apply mainly gross returns. However, there are some reasons for the use of logarithmic returns. First, we can derive approximate distributions for the stock price by applying limit theorems for the sum of the logarithmic returns, which makes the study of logarithmic returns interesting. Indeed, we can write
See (3.49) for a more detailed derivation of the log-normal model for stock prices. Second, taking logarithms of returns transforms the original time series of prices to a stationary time series, as explained in the connection of Figure 5.1.
For a statistical modeling we need typically a stationary time series. Stationarity is defined in Section 5.1. For example, autoregressive moving average processes (ARMA) and generalized autoregressive conditional heteroskedasticity (GARCH) models, defined in Section 5.3, are stationary time series models. The original time series of stock prices is not a stationary time series, but it can be argued that a return time series is close to stationarity.4
Note that we can write, analogously to (2.2),

Thus, we can derive approximate distributions for the stock price by applying limit theorems for the sum of the price differences. See (3.46) for a more detailed derivation of the normal model for stock prices. The time series of price differences is not a stationary time series, as discussed in the connection of Figure 5.2. However, for short time periods a time series of price differences can be approximately stationary. Thus, modeling price differences instead of returns can be reasonable.
2.2 Fixed Income Instruments
One unit of currency today is better than one unit of currency tomorrow. Fixed income research studies how much one should pay today, in order to receive a cash payment at a future day.
Fixed income instruments are described in more detail in Chapter 18. Here we give an overview of zero-coupon bonds, coupon paying bonds, interest rates, and of calculation of bond returns.
2.2.1 Bonds
Bonds include zero-coupon bonds and coupon bearing bonds.
- 1. A zero-coupon bond, or a pure discount bond, is a certificate which gives the owner a nominal amount
 (principal) at the future maturity time
(principal) at the future maturity time  . Typically we take
. Typically we take  .
. - 2. Coupon bearing bonds make regular payments (coupons) before the final payment at the maturity. A coupon bond can be defined as a series of payments
 at times
at times  . The terminal payment contains the principal and the final coupon payment.5
. The terminal payment contains the principal and the final coupon payment.5
A zero-coupon bond is a more basic instrument than a coupon bond, because a coupon bond can be defined as a portfolio of zero-coupon bonds. Let ![]() be the price of a coupon bond which starts at
be the price of a coupon bond which starts at ![]() and makes payments
and makes payments ![]() at times
at times ![]() , where
, where ![]() . It holds that
. It holds that

where ![]() are the prices of zero-coupon bonds starting at
are the prices of zero-coupon bonds starting at ![]() with maturity
with maturity ![]() , and with principal
, and with principal ![]() .
.
The cash flow generated by a bond is determined when the bond is issued. The bond can be traded before its maturity and its price can fluctuate before the maturity. For example, the price of a zero-coupon bond with the nominal amount ![]() is equal to
is equal to ![]() at the maturity, but its price fluctuates until the maturity is reached. The price fluctuates as a function of interest rate fluctuation. Thus, bonds bear interest rate risk if they are not kept until maturity. If the bonds are kept until maturity they bear the inflation risk and the risk of the default of the issuer.
at the maturity, but its price fluctuates until the maturity is reached. The price fluctuates as a function of interest rate fluctuation. Thus, bonds bear interest rate risk if they are not kept until maturity. If the bonds are kept until maturity they bear the inflation risk and the risk of the default of the issuer.
Bonds can be divided by the issuer. The main classes are government bonds, municipal bonds, and corporate bonds. Credit rating services give credit ratings to the bond issuers. Credit ratings help the investors to evaluate the probability of the payment default. Credit rating services include Standard & Poor's and Moody's.
US Treasury securities are backed by the US government. US Treasury securities include Treasury bills, Treasury notes, and Treasury bonds.
- 1. Treasury bills are zero-coupon bonds with original time to maturity of 1 year or less.6
- 2. Treasury notes are coupon bonds with original time to maturity between 2 and 10 years.
- 3. Treasury bonds are coupon bonds with original time to maturity of more than 10 years.
Widely traded German government bonds include Bundesschatzanweisungen (Schätze), which are 2 year notes, Bundesobligationen (Bobls), which are 5 year notes, and Bundesanleihen (Bunds and Buxl), which are 10 and 30 year bonds.
There are many types of fixed income securities. Callable bonds are such bonds that allow the bond issuer to purchase the bond back from the bondholders. The callable bonds make it possible for the issuer to retire old high-rate bonds and issue new low-rate bonds. Floating rate bonds (floaters) are such bonds whose rates are adjusted periodically to match inflation rates. Treasury STRIPS are such fixed income securities where the principal and the interest component of US Treasury securities are traded as separate zero coupon securities. The acronym STRIPS means separate trading of registered interest and principal securities.
2.2.2 Interest Rates
Interest rates are the basis for many financial contracts. We can separate between the government rates and the interbank rates. The government rates are deduced from the bonds issued by the governments and the interbank rates are obtained from the rates at which deposits are exchanged between banks.
Libor (London interbank offered rate) and Euribor (Euro interbank offered rate) are important interbank rates. Eonia (Euro overnight index average) is an overnight interest rate within the eurozone, but unlike the Euribor and Libor does not include term loans. Eonia is similar to the federal funds rate in the US. Sonia (Sterling overnight index average) is the reference rate for overnight unsecured transactions in the Sterling market.
Euribor and Libor are comparable base rates. Euribor rates are trimmed averages of interbank interest rates at which a collection of European banks are prepared to lend to one another. Libor rates are trimmed averages of interbank interest rates at which a collection of banks on the London money market are prepared to lend to one another. Euribor and Libor rates come in different maturities. In contrast to Euribor rates, the Libor rates come in different currencies. Euribor and Libor rates are not based on actual transactions, whereas Eonia is based on actual transactions. A study published in May 2008 in The Wall Street Journal suggested that the banks may have understated the borrowing costs. This led to reform proposals concerning the calculation of the Libor rates.
The Eonia rate is the rate at which banks provide unsecured loans to each other with a duration of 1 day within the Euro area. The Eonia rate is a volume weighted average of transactions on a given day and it is computed by the European Central Bank by the close of the real-time gross settlement on each business day. Eonia can be considered as the 1 day Euribor rate or as the Euro version of overnight index swaps (OIS). The Eonia panel consists of over 50 mostly European banks. The banks are chosen to the panel based on their premium credit rating and the high volume of their money market transactions conducted within the Eurozone. Banks on the Eonia panel are the same banks included in the Euribor panel.
Euribor rates are used as a reference rate for euro-denominated forward rate agreements, short term interest rate futures contracts, and interest rate swaps. Libor rates are used for Sterling and US dollar-denominated instruments.
2.2.2.1 Definitions of Interest Rates
The different definitions of interest rate are discussed in detail in Chapter 18. As an example we can consider a loan where the interest is paid at the end of a given period, and the interest is quoted in annual rate. Rate conventions determine how the quoted annual rate relates to the actual payment. Maybe the most common convention is to pay ![]() , where
, where ![]() is the principal,
is the principal, ![]() is the annual rate, and
is the annual rate, and ![]() is the number of calendar days of the deposit or loan. Note that loan rates are either rates that apply to a loan starting now until a given expiry, or forward rates, that are rates applying to a loan starting in the future for a given period of time.
is the number of calendar days of the deposit or loan. Note that loan rates are either rates that apply to a loan starting now until a given expiry, or forward rates, that are rates applying to a loan starting in the future for a given period of time.
Rates are quoted in percents but they are compared in basis points, where a basis point is ![]() , that is,
, that is, ![]() is 100 basis points.
is 100 basis points.
2.2.2.2 The Risk Free Rate
The risk free rate is different depending on the investment horizon. For one day horizon the risk free rate could be the Eonia rate or the rate of a bank account, and for 1 month horizon the risk free rate could be the rate of 1 month government bond.
2.2.3 Bond Prices and Returns
A 10 year zero-coupon bond has the time to maturity of 10 years at the emission, after 1 year the time to maturity is 9 years, after 2 years the time to maturity is 8 years, and so on. The price of the zero-coupon bond is fluctuating according to the fluctuation of the interest rates, until the price equals the nominal value at the maturity. Thus, the price of the 10 year zero-coupon bond gives information about the 10 year interest rate at the emission, after 1 year the price of the bond gives information about the 9 year interest rate, after 2 years the price of the bond gives information about the 8 year interest rate, and so on.
Information of the bond markets is given by data providers in terms of the yields. The yield of a zero-coupon bond is defined as
where ![]() is the time to maturity in fractions of a year, and
is the time to maturity in fractions of a year, and ![]() is the bond price with
is the bond price with ![]() . The price of a bond can be written in terms the yield as
. The price of a bond can be written in terms the yield as
See Section 18.1.2 for a discussion of the yield of a zero-coupon bond.
Let ![]() , where
, where ![]() is the expiration day of the zero-coupon bond. The prices are
is the expiration day of the zero-coupon bond. The prices are ![]() and
and ![]() . The return of a bond trader is equal to
. The return of a bond trader is equal to
where we used the fact ![]() .
.
Data providers give a time series ![]() of yields of a
of yields of a ![]() year bond, where
year bond, where
where ![]() are the time points of sampling. How to obtain a time series
are the time points of sampling. How to obtain a time series ![]() of the returns of a bond investor? Let us denote
of the returns of a bond investor? Let us denote ![]() ,
, ![]() , and
, and ![]() . Then
. Then ![]() . Let us make approximation
. Let us make approximation
Then (2.4) implies
where ![]() is the length of the sampling interval in fractions of a year. For example, with monthly sampling
is the length of the sampling interval in fractions of a year. For example, with monthly sampling ![]() .
.
2.3 Derivatives
Derivatives are financial assets whose payoff is defined in terms of more basic assets. We describe first forwards and futures, and after that we describe options. For many assets trading with derivatives is more active than trading with the basic assets. For example, exchange rates and commodities are traded more actively in the future markets than in the spot markets.
Over-the-counter (OTC) derivatives are traded directly between two counterparties. Exchange traded derivatives are traded in an exchange, which acts as an intermediary party between the traders.
2.3.1 Forwards and Futures
First we define forwards and futures. After that we give examples of some actively traded futures. Forwards are derivatives traded over the counter whereas futures contracts are traded on exchanges. The underlyings of a forward or a futures contract can be stocks (single-stock futures), commodities, currencies, interest rates, or stock indexes, for example.
2.3.1.1 Forwards
A forward is a contract written at time ![]() , with a commitment to accept delivery of (or to deliver) the specified number of units of the underlying asset at a future date
, with a commitment to accept delivery of (or to deliver) the specified number of units of the underlying asset at a future date ![]() , at forward price
, at forward price ![]() , which is determined at
, which is determined at ![]() .
.
At time ![]() nothing changes hands, all exchanges will take place at time
nothing changes hands, all exchanges will take place at time ![]() . A long position is a commitment to accept the delivery at time
. A long position is a commitment to accept the delivery at time ![]() . A short position is a commitment to deliver the contracted amount. The current price of the underlying is called the spot price.
. A short position is a commitment to deliver the contracted amount. The current price of the underlying is called the spot price.
2.3.1.2 Futures
A futures contract can be considered as a special case of a forward contract. An instrument is called a futures contract if the trading is done in a futures exchange, where the forward commitment is made through a homogenized contract so that the size of the underlying asset, the quality of the underlying asset, and the expiration date are preset. In addition, futures exchanges require a daily mark-to-market of the positions.
A futures exchange acts as an intermediary between the participants of a futures contract. The existence of the intermediary minimizes the risk of the default of the participants of the contract. When a participant enters a futures contract the exchange requires to put up an initial amount of liquid assets into the margin account. Marking to market means that the daily futures price is settled daily so that the exchange will draw money out of one party's margin account and put it into the others so that the daily loss or profit is taken into account. If the margin account goes below a certain value, then a margin call is made and the account owner must add money to the margin account. In contrast to futures contracts, forward contracts may not require any marking to market until the expiration day.
A futures contract can be settled with cash or with the delivery of the underlying. For example, if the underlying of the futures contract is a stock index, then the futures contract is usually settled with cash. A futures contract can be closed before the expiration day by entering the opposite direction futures contract.
On the delivery date, the amount exchanged is not the specified price on the contract but the spot value (i.e., the original value agreed upon, since any gain or loss has already been previously settled by marking to market).
The situation where the price of a commodity for future delivery is higher than the spot price, or where a far future delivery price is higher than a nearer future delivery, is known as contango. The reverse, where the price of a commodity for future delivery is lower than the spot price, or where a far future delivery price is lower than a nearer future delivery, is known as backwardation.
2.3.2 Options
We describe calls and puts, applications of options, and some exotic options.
2.3.2.1 Calls and Puts
The buyer of a call option receives the right to buy the underlying instrument and the buyer of a put option receives the right to sell the underlying instrument.
An European call option gives the right to buy an asset at the given expiration time ![]() at the given strike price
at the given strike price ![]() . An European put option gives the right to sell an asset at the given expiration time
. An European put option gives the right to sell an asset at the given expiration time ![]() at the given strike price
at the given strike price ![]() . Let us denote with
. Let us denote with ![]() the price of an European call option at time
the price of an European call option at time ![]() and with
and with ![]() the price of the asset. The value
the price of the asset. The value ![]() of the European call option at the expiration time
of the European call option at the expiration time ![]() is equal to
is equal to
Let us denote with ![]() the price of a put option at time
the price of a put option at time ![]() . The value of the European put option at the expiration time
. The value of the European put option at the expiration time ![]() is equal to
is equal to
American options have a different mode concerning the right to exercise the option than the European options. American call and put options can be exercised at any time before the expiration date, whereas European options can be exercised only at the expiration day. Thus an American option is more expensive than the corresponding European option. When we use the term “option” without a further qualification, then we refer to an European option.
The following terminology is used to describe options.
-
A call option is out of the money if
 . A call option is at the money if
. A call option is at the money if  . A call option is in the money if
. A call option is in the money if  . A call option is deep out of the money (deep in the money) if
. A call option is deep out of the money (deep in the money) if  (
(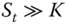 ).
).The moneyness of a call option is defined as
 . The moneyness of a put option is defined as
. The moneyness of a put option is defined as  .7
.7 - Before the expiration time
 the price of a call option satisfies
the price of a call option satisfies

see (14.10). The difference
 is called the time value of the option. The value
is called the time value of the option. The value  is called the intrinsic value. Thus,2.6
is called the intrinsic value. Thus,2.6
2.3.2.2 Applications of Options
Options can serve at least the following purposes:
- 1. Options can be used to create a large number of different payoffs. Some payoffs applied in option trading are described in Chapter 17. For example, buying a call and a put with the same strike price and the same expiration creates a straddle position which profits from large positive or negative movements of the underlying.
- 2. Options can provide insurance. With options it is possible to create a payoff which cuts the losses that could occur without using of the options. Buying a put option gives an insurance in the case one has to sell in a future time an asset one possesses. Buying a call option gives an insurance in the case when one has to buy in a future time an asset one does not possess. Examples of providing insurance with options include the following:
- Buying a put option on a stock gives an insurance policy for an investor. If an investor owns a stock, buying a put option will cut the future possible losses.
- Buying a put option on an exchange rate gives an insurance policy for a company receiving payments on a foreign currency in future.
- 3. Call options can be used to give a compensation to managers, since the payoff of a call option is positive only when the stock price is larger than the strike price.
- 4. Options make leveraging possible, since option trading requires a small initial capital as compared to stock trading.8
2.3.2.3 Exotic Options
We say that an option is exotic if it is not an European or an American call or put option.
Bermudan Options
There exists three basic modes concerning the right to exercise the option: European, American, and Bermudan. A Bermudan option can be exercised at some times or time periods before the expiration. whereas European options can be exercised only at the expiration date, and American options can be exercised at any time before the expiration.
Asian Options
The value of an Asian call option at the expiration is
where

with ![]() being a collection of predetermined time points. Asian options are more resistant to manipulation than European options: The value of an European option at the expiration depends on the value of the underlying asset at one time point (the expiration date), whereas the value of an Asian option depends on the values of the underlying asset at several time points.
being a collection of predetermined time points. Asian options are more resistant to manipulation than European options: The value of an European option at the expiration depends on the value of the underlying asset at one time point (the expiration date), whereas the value of an Asian option depends on the values of the underlying asset at several time points.
Barrier Options
Barrier options disappear if the underlying either exceeds, or goes under the barrier. Alternatively, a barrier option could have value only if it has exceeded, or went under the barrier. Knock-in options come into existence if some barrier is hit and knock-out options cease to exist if some barrier is hit. One speaks of up-and-out, down-and-out, up-and-in, down-and-in options. For example, a knock-out option on stock ![]() , written at time 0, with expiration time
, written at time 0, with expiration time ![]() , has the payoff
, has the payoff

where ![]() is the strike price, and
is the strike price, and ![]() is the barrier. Barrier options are cheaper than the corresponding European options, which makes them useful.
is the barrier. Barrier options are cheaper than the corresponding European options, which makes them useful.
Multiasset Options
Multiasset options involve many underlying assets and many strike prices. We give some examples of multiasset options.
- 1. A call can be generalized to a multiasset option with payoff

- where
 and
and  are the underlying assets and
are the underlying assets and  are strike prices. A payoff can have elements of a call and a put:
are strike prices. A payoff can have elements of a call and a put:

- 2. The payoff of an option on a linear combination can be written as

- where
 is a payoff function,
is a payoff function,  are assets, and
are assets, and  are weights. For example, an option on a linear combination can be an option on an index or an option on a spread.
are weights. For example, an option on a linear combination can be an option on an index or an option on a spread. - 3. Outperformance options are calls on the maximum and puts on the minimum. We have that

Thus, the payoff of an outperformance option can be written as a payoff of a linear combination of the underlying and an option on the spread between the underlyings.
- 4. The payoff of a univariate digital option is
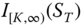 , where
, where 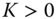 is the strike price. The option pays one unit at the maturity time if the value of the underlying exceeds the strike price. The bivariate digital option pays one unit if both of the underlyings exceed the respective strike prices. The payoff is
is the strike price. The option pays one unit at the maturity time if the value of the underlying exceeds the strike price. The bivariate digital option pays one unit if both of the underlyings exceed the respective strike prices. The payoff is

- 5. The payoff of an option written on a basket can be written as

- where
 is a univariate function and
is a univariate function and  is a multivariate function. For example,
is a multivariate function. For example,  and
and  , or
, or  .
.
2.4 Data Sets
We describe the data sets which are used to illustrate the methods throughout the book. Some additional data are described in Section 6.3.
2.4.1 Daily S&P 500 Data
The daily S&P 500 data consists of the daily closing prices starting at January 4, 1950 and ending at April 2, 2014, which gives 16,046 daily observations.9
Figure 2.1 shows (a) the daily closing prices ![]() and (b) the returns
and (b) the returns ![]() of S&P 500.
of S&P 500.

Figure 2.1 S&P 500 index. (a) Daily closing prices of S&P 500 and (b) daily returns.
2.4.2 Daily S&P 500 and Nasdaq-100 Data
The S&P 500 and Nasdaq-100 data consists of the daily closing prices starting at October 1, 1985 and ending at May 21, 2014, which gives 7221 daily observations.10
Figure 2.2 shows (a) the normalized prices and (b) a scatter plot of the returns of S&P 500 and Nasdaq-100. S&P 500 prices is shown with black and the Nasdaq-100 prices is shown with red. The prices are normalized so that they start with value one for both indexes. (Note that the normalized price is the cumulative wealth when the initial wealth is one.)

Figure 2.2 S&P 500 and Nasdaq-100 indexes. (a) The prices of S&P 500 (black) and Nasdaq-100 (red). The prices are normalized to start at value one. (b) A scatter plot of the daily returns of S&P 500 and Nasdaq-100.
2.4.3 Monthly S&P 500, Bond, and Bill Data
The data consists of the monthly returns of S&P 500 index, monthly returns of US Treasury 10 year bond, and monthly rates of US Treasury 1 month bill. The data starts at May 1953 and ends at December 2013, which gives 728 monthly observations.11 The 10 year bond returns are calculated from the yields as in (2.5).
Figure 2.3 shows (a) cumulative wealth and (b) a scatter plot of returns of S&P 500 and 10 year bond. The cumulative wealth is ![]() , where
, where ![]() are the gross returns. The cumulative wealth of S&P 500 is shown with black, 10 year bond with red, and 1 month bill with blue. Figure 2.4 shows (a) the treasury bill rates (blue) and (b) the yields of 10 year Treasury bond (red).
are the gross returns. The cumulative wealth of S&P 500 is shown with black, 10 year bond with red, and 1 month bill with blue. Figure 2.4 shows (a) the treasury bill rates (blue) and (b) the yields of 10 year Treasury bond (red).

Figure 2.3 S&P 500, US Treasury 10 year bond, and 1 month bill. (a) The cumulative wealth of S&P 500 (black), 10 year bond (red), and 1 month bill (blue). The cumulative wealths are normalized to start at value one. (b) A scatter plot of monthly returns of S&P 500 and 10 year bond.

Figure 2.4 US Treasury bill rates and 10 year bond yields. (a) Treasury bill rates (blue). (b) Yields of 10 year Treasury bond (red).
2.4.4 Daily US Treasury 10 Year Bond Data
The US Treasury 10 year bond data consists of the daily yields starting at January 2, 1962 and ending at March 3, 2014, which gives 13,006 daily observations.12 We have described the US 10 year Treasury bonds in Section 2.2.1.
Figure 2.5 shows (a) the daily yields and (b) the daily returns of the US 10 year Treasury bond. The 10 year bond returns are calculated from the yields as in (2.5).

Figure 2.5 10 year US Treasury bond. (a) Daily yields of the 10 year US Treasury bond and (b) daily returns of the bond.
2.4.5 Daily S&P 500 Components Data
The S&P 500 components data consists of daily closing prices of 312 stocks, which were components of S&P 500 at May 23, 2014. The data starts September 30, 1991 and ends at May 23, 2014. There are 5707 daily observations.
Figure 2.6(a) shows the normalized prices of the stocks. The prices are normalized to have value one at the beginning. Panel (b) shows a scatter plot of points ![]() , where
, where ![]() are the 95% empirical quantiles of the negative returns of the
are the 95% empirical quantiles of the negative returns of the ![]() th stock, and
th stock, and ![]() are the annualized sample means of the returns of the
are the annualized sample means of the returns of the ![]() th stock.13
th stock.13

Figure 2.6 S&P 500 components. (a) Time series of the normalized prices of the components. (b) A scatter plot of  , where
, where  are the 95% empirical quantiles of the negative returns, and
are the 95% empirical quantiles of the negative returns, and  are the annualized sample means of the returns.
are the annualized sample means of the returns.
where ![]() is a constant.
is a constant.



