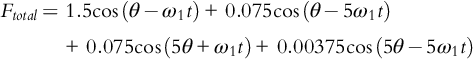3.8.1 Subharmonic Torques in a Voltage-Source-Fed Induction Motor

The equivalent circuit of a voltage-source-fed induction motor is shown in Fig. 3.38a for the fundamental (h = 1) and for the harmonic of order h. Using Thevenin’s theorem (subscript TH), the magnetizing branch can be eliminated (Fig. 3.38b) and one obtains the following relation for the electrical torque of the hth harmonic where $V_{\mathit{shTH}}=\left|{\tilde{V}}_{\mathit{shTH}}\right|:$

$T_{\mathrm{e}\mathrm{h}}=\frac{1}{{\omega }_{\mathrm{m}\mathrm{s}\mathrm{h}}}\frac{q_1{V}_{\mathit{shTH}}^2{R}_r^{\prime }/s_h}{{\left(R_{\mathit{shTH}}+R_r^{\prime }/s_h\right)}^2+{\left(h{\omega }_1\left(L_{\mathit{s\ell TH}}+L_{r\ell }^{\prime }\right)\right)}^2}\text{.}$

The Thevenin-adjusted machine parameters are

$V_{\mathit{shTH}}=\frac{V_{sh}\left(h{\omega }_1{L}_m\right)\angle {\theta }_{hTH}}{\sqrt{R_s^2+{\left(h{\omega }_1{L}_{s\ell }+h{\omega }_1{L}_m\right)}^2}}$

with

${\theta }_{hTH}=\frac{\pi }{2}-{tan}^{-1}\left[\frac{h{\omega }_1{L}_{s\ell }+h{\omega }_1{L}_m}{R_s}\right]\text{,}$

$R_{\mathit{shTH}}=\frac{h^2{\left({\omega }_1{L}_m\right)}^2{R}_s}{R_s^2+{\left(h{\omega }_1{L}_{s\ell }+h{\omega }_1{L}_m\right)}^2}\text{,}$

$\left(h{\omega }_1{L}_{\mathit{s\ell TH}}\right)=\frac{h\left({\omega }_1{L}_m\right)R_s^2+h^2\left({\omega }_1{L}_{s\ell }\right)\left({\omega }_1{L}_m\right)\left[h\left({\omega }_1{L}_{s\ell }\right)+h\left({\omega }_1{L}_m\right)\right]}{R_s^2+{\left(h{\omega }_1{L}_{s\ell }+h{\omega }_1{L}_m\right)}^2}\text{.}$

The mechanical synchronous angular velocity is

${\omega }_{msh}=\frac{h{\omega }_1}{\left(p/2\right)}\text{,}$

where ω₁ is the electrical synchronous angular velocity, p is the number of poles, and q₁ is the number of phases (e.g., q₁ = 3).

In order to obtain the maximum or breakdown torque one matches the impedances of the Thevenin-adjusted equivalent circuit at s_h = s_hmax:

$R_{rh}^2={\left(\frac{R_r^{\prime }}{s_{h\max }}\right)}^2=R_{\mathit{shTH}}^2+{\left[h{\omega }_1\left(L_{\mathit{s\ell TH}}+L_{r\ell }\right)\right]}^2\text{,}$

and the breakdown slip for the hth harmonic becomes

$s_{h\max }=\frac{R_r^{\prime }}{\pm \sqrt{R_{\mathit{shTH}}^2+{\left(h{\omega }_1\left(L_{\mathit{s\ell TH}}+L_{r\ell }^{\prime }\right)\right)}^2}}\text{.}$

The maximum motoring (mot) positive torque and the maximum generator (gen) negative torque for the time harmonic of hth order are

$T_{eh\max }^{mot}=\frac{1}{{\omega }_{msh}}\frac{q_1{V}_{\mathit{shTH}}^2{R}_r^{\prime }/\left|s_{h\max }\right|}{{\left(R_{\mathit{shTH}}+R_r^{\prime }/\left|s_{h\max }\right|\right)}^2+{\left(h{\omega }_1\left(L_{\mathit{s\ell TH}}+L_{r\ell }^{\prime }\right)\right)}^2}\text{,}$

$T_{eh\max }^{gen}=-\frac{1}{{\omega }_{msh}}\frac{q_1{V}_{\mathit{shTH}}^2{R}_r^{\prime }/\left|s_{h\max }\right|}{{\left(R_{\mathit{shTH}}-R_r^{\prime }/\left|s_{h\max }\right|\right)}^2+{\left(h{\omega }_1\left(L_{\mathit{s\ell TH}}+L_{r\ell }^{\prime }\right)\right)}^2}\text{.}$

The generator (gen) electrical torque reaches its absolute (abs) maximum, if

$R_{\mathit{shTH}}=R_r^{\prime }/\left|s_{h\max }\right|\text{,}$

that is,

$\begin{array}{c}{T}_{eh\max }^{gen\mathit{abs}}=-\frac{1}{{\omega }_{msh}}\frac{q_1{V}_{\mathit{shTH}}^2{R}_r^{\prime }/\left|s_{h\max }\right|}{{\left(h{\omega }_1\left(L_{\mathit{s\ell TH}}+L_{r\ell }^{\prime }\right)\right)}^2}\\ =-\frac{\left(p/2\right)}{\left(h{\omega }_1\right)}\frac{q_1{V}_{\mathit{shTH}}^2{R}_{\mathit{shTH}}}{{\left(h{\omega }_1\left(L_{\mathit{s\ell TH}}+L_{r\ell }^{\prime }\right)\right)}^2}\text{.}\end{array}$

3.8.2 Subharmonic Torques in a Current-Source-Fed Induction Motor

The equivalent circuits of a current-source-fed induction motor are shown in Fig. 3.39a,b for the fundamental (h = 1) and for the harmonic of order h.

The torque of the hth time harmonic is, from Fig. 3.39b,

$T_{eh}=\frac{1}{{\omega }_{msh}}\frac{q_1{V}_{sh}^2{R}_r^{\prime }/s_h}{{\left(R_r^{\prime }/s_h\right)}^2+{\left(h{\omega }_1\left(L_m+L_{r\ell }^{\prime }\right)\right)}^2}\text{,}$

where ${\tilde{V}}_{sh}=jh{\omega }_1{L}_m{\tilde{I}}_{sh}$.

The breakdown slip is

$s_{h\max }=\pm R_r^{\prime }/\left(h{\omega }_1\left(L_m+L_{r\ell }^{\prime }\right)\right)\text{.}$

Two application examples will be presented where an induction motor is first fed by a voltage source and then by a current source containing a forward rotating subharmonic component of 6 Hz (h = 0.1).

3.8.3 Application Example 3.7: Computation of Forward-Rotating Subharmonic Torque in a Voltage-Source-Fed Induction Motor

Terminal voltages of a three-phase induction motor contain the forward-rotating subharmonic of 6 Hz at an amplitude of V_0.1 = 5%. The fundamental voltage is V₁ = 240 V and the parameters of a three-phase induction machine are as follows:

$\begin{array}{l}240/416\mathrm{V},\mathrm{\Delta }/\mathrm{Y}\mathrm{connected},f=60\mathrm{Hz},\\ n_{\mathrm{rated}}=1738\mathrm{rpm},p=4\mathrm{poles},\\ R_s=7.0\mathrm{\Omega },{\omega }_1{L}_{sl}=8\mathrm{\Omega },{\omega }_1{L}_m=110\mathrm{\Omega },\\ R_r^{\prime }=5\mathrm{\Omega },{\omega }_1{L}_{r\ell }^{\prime }=7\mathrm{\Omega }\text{.}\end{array}$

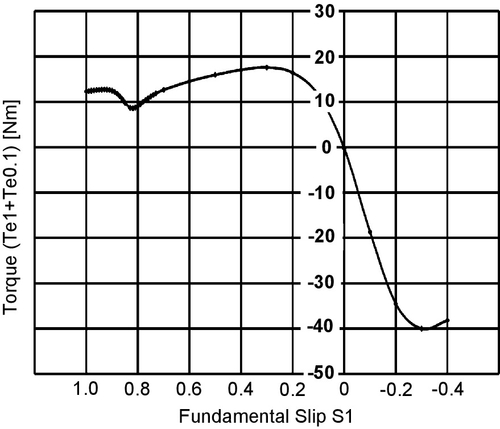
Compute and plot the sum of the fundamental and subharmonic torques (T_e1 + T_e0.1) as a function of the fundamental slip s₁.

Solution to Application Example 3.7

Parameters of Eqs. 3-47 to 3-54 are listed as a function of the fundamental (h = 1) and subharmonic h = 0.1 in Table E3.7.1. Fundamental torque values T_e1 are listed in Table E3.7.2 as a function of the fundamental slip s₁.

The plot of the positively rotating fundamental torque characteristic T_e1 = f(s₁) is shown in Fig. E3.7.1 and the positively rotating torque Te_0.1 = f(s_0.1) is depicted in Fig. E3.7.2, where the 6 Hz voltage component has an amplitude of 5%, that is, V_6Hz = 0.05 · V_60Hz = 0.05(240 V) = 12 V.

Subharmonic torque values T_e0.1 are listed in Table E3.7.3 as a function of the subharmonic slip s_0.1.

Using Eqs. 3-4d and 3-25 one can compute the fundamental torque T_e1 and the subharmonic torque T_e0.1 as a function of the fundamental slip s₁ (Table E3.7.4). For example a subharmonic (h = 0.1) slip of s_0.1 = 1 corresponds to a fundamental slip of (see Eqs. 3-31b, 3-32, and Table E3.7.3)

$s_1=\left(0.1\right)\left(s_{0.1}\right)+0.9=1.0\text{.}$

The plot of fundamental and subharmonic torque values (T_e1 + T_e0.1) as a function of fundamental slip (s₁) is shown in Fig. E3.7.3.

3.8.4 Application Example 3.8: Rationale for Limiting Harmonic Torques in an Induction Machine

Based on results of the previous application example, explain why low-frequency subharmonic voltages at the terminal of induction machines should be limited.

Solution to Application Example 3.8

For subharmonic slip s_0.1 = 1.0 one obtains with Eq. E3.7-2 the fundamental slip s₁ = 1.0. Correspondingly for subharmonic slip s_0.1 = 0.82 one obtains s₁ = 0.982, and for subharmonic slip s_0.1 = –0.82 one obtains s₁ = 0.818 (see Table E3.7.3).

One notes that the subharmonic torque at 6 Hz (h = 0.1) is relatively large in the generator region (T_e0.1 = –4.61 Nm). If the worst case is considered as defined by Eq. 3-52 the corresponding low-frequency harmonic torque is even larger. This is the reason why the low-frequency harmonic voltages should be limited to less than a few percent (e.g., 2%) of rated voltage.

3.8.5 Application Example 3.9: Computation of Forward-Rotating Subharmonic Torque in Current-Source-Fed Induction Motor

Terminal currents of a three-phase induction motor contain a forward-rotating subharmonic of 6 Hz at an amplitude I_0.1 = 5% of the fundamental I₁ = 1.73 A. The parameters of a three-phase induction machine are as follows:

$\begin{array}{l}3\mathrm{A}/1.73\mathrm{A},\mathrm{\Delta }/\mathrm{Y}\mathrm{connected},\mathrm{f}=60\mathrm{Hz},\\ n_{\mathrm{rat}}=1773\mathrm{rpm},\mathrm{p}=4\mathrm{poles},\\ R_s=7.0\mathrm{\Omega },{\omega }_1{L}_{s\mathrm{L}}=5\mathrm{\Omega },{\omega }_1{L}_m=110\mathrm{\Omega },\\ R_r^{\prime }=5\mathrm{\Omega },{\omega }_1{L}_{r\ell }^{\prime }=4\mathrm{\Omega }\text{.}\end{array}$

Compute the fundamental torque (T_e1) as a function of the fundamental slip (s₁) and subharmonic torque (T_e0.1) as a function of the subharmonic slip (s_0.1).

Solution to Application Example 3.9

The parameters of Eqs. 3-53 and 3-54 and the corresponding fundamental and subharmonic torques are listed in Tables E3.9.1 through E3.9.3 as a function of the fundamental h = 1 and the subharmonic h = 0.1.

Table E3.9.1

Maximum Torques for Fundamental and Subharmonic Currents, where the Fundamental Current is 1.73 A and the Subharmonic Current is 5% of the Fundamental Current

h	$\mathbf{\left|}{\tilde{\mathit{V}}}_{\mathbf{s}\mathbf{h}}\right|$ (V)]	± Shmax (–)	ωmsh (rad/s)	Teh maxmot (Nm)	Teh maxgen (Nm)
1	190.3	0.044	188.49	2.53	–2.35
0.1	0.952	0.439	18.849	0.0063	–0.0063

One notes that the low-frequency harmonic torques at 6 Hz and 5% harmonic current amplitudes are very small (about 0.0063 Nm).

3.9.1 Application Example 3.10: Computation of Rotating MMF with Time and Space Harmonics

Compute the mmf and its angular velocities for an induction machine with the following time and space harmonics:

(a) A₁ = 1 pu, A_H = 0.05 pu, I_m1 = 1 pu, I_mh = 0.05 pu, H = 5, and h = 5.

(b) A₁ = 1 pu, A_H = 0.05 pu, I_m1 = 1 pu, I_mh = 0.05 pu, H = 13, and h = 0.5.

Solution to Application Example 3.10

a) For A₁ = 1 pu, A_H = 0.05 pu, I_m1 = 1 pu, I_mh = 0.05 pu, H = 5, and h = 5 one obtains the rotating mmf as

$F_{\mathit{total}}=1.5\cos \left(\theta –{\omega }_{1}t\right)+0.075\cos \left(\theta –5{\omega }_{1}t\right)+0.075\cos \left(5\theta +{\omega }_{1}t\right)+0.00375\cos \left(5\theta –5{\omega }_{1}t\right)$

with the angular velocities

$\begin{array}{l}\frac{d{\theta }_{h=1}}{dt}={\omega }_1,\frac{d{\theta }_{h=5}}{dt}=5{\omega }_1,\frac{d{\theta }_{H=5}}{dt}=-{\omega }_1/5,\\ \frac{d{\theta }_{H=5,h=5}}{dt}={\omega }_1\text{,}\end{array}$

b) For A₁ = 1 pu, A_H = 0.05 pu, I_m1 = 1 pu, I_mh = 0.05 pu, H = 13, and h = 0.5 one obtains the rotating mmf as

$F_{\mathit{total}}=1.5\cos \left(\theta -{\omega }_{1}t\right)+0.075\cos \left(\theta -0.5{\omega }_{1}t\right)+0.075\cos \left(13\theta -{\omega }_{1}t\right)+0.0035\cos \left(13\theta -0.5{\omega }_{1}t\right)$

with the angular velocities

$\begin{array}{l}\frac{d{\theta }_{h=1}}{dt}={\omega }_1,\frac{d{\theta }_{h=0.5}}{dt}=0.5{\omega }_1,\frac{d{\theta }_{H=13}}{dt}={\omega }_1/13,\\ \frac{d{\theta }_{H=13,h=0.5}}{dt}={\omega }_1/26\text{.}\end{array}$

3.9.2 Application Example 3.11: Computation of Rotating MMF with Even Space Harmonics

Nonideal induction machines may generate even space harmonics. For A₁ = 1 pu, A_H = 0.05 pu, I_m1 = 1 pu, I_mh = 0.05 pu, H = 12, and h = 0.1, compute the resulting rotating mmf and its angular velocities.

Solution to Application Example 3.11

$F_{\mathrm{total}}=1.5cos\left(\theta –{\omega }_{1}t\right)+0.075cos\left(\theta –0.1{\omega }_{1}t\right)$

with the angular velocities

$\frac{d{\theta }_{h=1}}{dt}={\omega }_1,\frac{d{\theta }_{h=0.1}}{dt}=0.1{\omega }_1\text{.}$

3.9.3 Application Example 3.12: Computation of Rotating MMF with Noninteger Space Harmonics

Nonideal induction machines may generate noninteger space harmonics. For A₁ = 1 pu, A_H = 0.05 pu, I_m1 = 1 pu, I_mh = 0.05 pu, H = 13.5, and h = 0.1, compute the resulting rotating mmf and its angular velocities.

Solution to Application Example 3.12

$\begin{array}{l}{F}_{\mathrm{total}}=1.5cos\left(\theta –{\omega }_{1}t\right)+0.75cos\left(\theta –0.1{\omega }_{1}t\right)+0.025\{cos\left(13.5\theta –{\omega }_{1}t\right)+cos\left(13.5\theta –60°–{\omega }_{1}t\right)+cos(13.5\theta +60°\\ –{\omega }_{1}t\left)\right\}+0.025\left\{cos\left(13.5\theta +{\omega }_{1}t\right)+cos\left(13.5\theta +60°+{\omega }_{1}t\right)+cos\left(13.5\theta –60°+{\omega }_{1}t\right)\right\}+0.00125\{cos(13.5\theta –0.1\\ {\omega }_{1}t)+cos\left(13.5\theta –60°–0.1{\omega }_{1}t\right)+cos\left(13.5\theta +60°–0.1{\omega }_{1}t\right)\}+0.00125\{cos\left(13.5\theta –0.1{\omega }_{1}t\right)+cos(13.5\theta +60°+\\ 0.1{\omega }_{1}t)+cos\left(13.5\theta –60°+0.1{\omega }_{1}t\right)\}\text{,}\end{array}$

with the angular velocities

$\begin{array}{l}\frac{d{\theta }_{h=1}}{dt}={\omega }_1,\frac{d{\theta }_{h=0.1}}{dt}=0.1{\omega }_1,\frac{d{\theta }_{H=13.5}}{dt}=\pm {\omega }_1/13.5,\\ \frac{d{\theta }_{H=13.5,h=0.1}}{dt}=\pm {\omega }_1/13.5\text{.}\end{array}$

Application Examples 3.10 to 3.12 illustrate how sub- and noninteger harmonics are generated by induction machines. Such harmonics may cause the malfunctioning of protective (e.g., under-frequency) relays within a power system [42].

The calculation of the asynchronous torques due to harmonics and inter- and subharmonics is based on the equivalent circuit without taking into account the variation of the differential leakage as a function of the numbers of stator slots and rotor slots. It is well known that certain stator and rotor slot combinations lead to asynchronous and synchronous harmonic torques in induction machines. A more comprehensive treatment of such parasitic asynchronous and synchronous harmonic torques is presented in [30,43–69]. Speed variation of induction motors is obtained either by voltage variation with constant frequency or by variation of the voltage and the fundamental frequency using inverters as a power source. Inverters have somewhat nonsinusoidal output voltages or currents. Thus parasitic effects like additional losses, dips in the torque–speed curve, output power derating, magnetic noise, oscillating torques, and harmonic line currents are generated. It has already been shown [43–45] that the multiple armature reaction has to be taken into account if effects caused by delta-connection of the stator windings, parallel winding branches, stator current harmonics, or damping of the air-gap field are to be considered. Moreover, the influence of the slot openings [46] and interbar currents [30,47,48,68] in case of slot skewing is important. Compared with conventional methods [25,30,68] the consideration of multiple armature reactions requires additional work consisting of the solution of a system of equations of the order from 14 to 30 for a three-phase induction machine and the summation of the air-gap inductances. The presented theory [69] is based on Fourier analysis and does not employ any transformation. As an alternative to the analytical method described [69] two-dimensional numerical methods (e.g., finite-element method) with time stepping procedures are available [49–51]. These have the advantages of analyzing transients, variable permeability, and eddy currents in solid iron parts, but have the disadvantages of grid generation, discretization errors, and preparatory work and require large computing CPU time.

3.11.1 Application Example 3.13: Calculation of Winding Stress Due to PMW Voltage-Source Inverters

Voltage ripples due to PWM voltage-source inverters cause voltage stress in windings of machines and transformers. The configuration of Fig. E3.13.1 represents a simple winding with two turns consisting of eight segments. Each segment can be represented by an inductance L_i, a resistance R_i, and a capacitance to ground (frame) C_i, and there are four interturn capacitances C_ij and inductances L_ij. Figure E3.13.2 represents a detailed equivalent circuit for the configuration of Fig. E3.13.1.

a) To simplify the analysis neglect the capacitances C_ij and the inductances L_ij. This leads to the circuit of Fig. E3.13.3, where the winding is fed by a PWM voltage source (see Fig. E3.13.4). One obtains the 16 differential equations (Eqs. E3.13-1a,b to E3.13-8a,b) as listed below.

$\frac{d{i}_1}{dt}=-\frac{R_1}{L_1}{i}_1-\frac{v_1}{L_1}+\frac{v_s\left(t\right)}{L_1}\text{,}$

$\frac{d{v}_1}{dt}=\frac{i_1}{C_1}-\frac{G_1}{C_1}{v}_1-\frac{i_2}{C_1}\text{,}$

$\frac{d{i}_2}{dt}=-\frac{R_2}{L_2}{i}_2-\frac{v_2}{L_2}+\frac{v_1}{L_2}\text{,}$

$\frac{d{v}_2}{dt}=\frac{i_2}{C_2}-\frac{G_2}{C_2}{v}_2-\frac{i_3}{C_2}\text{,}$

$\frac{d{i}_3}{dt}=-\frac{R_3}{L_3}{i}_3-\frac{v_3}{L_3}+\frac{v_2}{L_3}\text{,}$

$\frac{d{v}_3}{dt}=\frac{i_3}{C_3}-\frac{G_3}{C_3}{v}_3-\frac{i_4}{C_3}\text{,}$

$\frac{d{i}_4}{dt}=-\frac{R_4}{L_4}{i}_4-\frac{v_4}{L_4}+\frac{v_3}{L_4}\text{,}$

$\frac{d{v}_4}{dt}=\frac{i_4}{C_4}-\frac{G_4}{C_4}{v}_4-\frac{i_5}{C_4}\text{,}$

$\frac{d{i}_5}{dt}=-\frac{R_5}{L_5}{i}_5-\frac{v_5}{L_5}+\frac{v_4}{L_5}\text{,}$

$\frac{d{v}_5}{dt}=\frac{i_5}{C_5}-\frac{G_5}{C_5}{v}_5-\frac{i_6}{C_5}\text{,}$

$\frac{d{i}_6}{dt}=-\frac{R_6}{L_6}{i}_6-\frac{v_6}{L_6}+\frac{v_5}{L_6}\text{,}$

$\frac{d{v}_6}{dt}=\frac{i_6}{C_6}-\frac{G_6}{C_6}{v}_6-\frac{i_7}{C_6}\text{,}$

$\frac{d{i}_7}{dt}=-\frac{R_7}{L_7}{i}_7-\frac{v_7}{L_7}+\frac{v_6}{L_7}\text{,}$

$\frac{d{v}_7}{dt}=\frac{i_7}{C_7}-\frac{G_7}{C_7}{v}_7-\frac{i_8}{C_7}\text{,}$

$\frac{d{i}_8}{dt}=-\frac{R_8}{L_8}{i}_8-\frac{v_8}{L_8}+\frac{v_7}{L_8}\text{,}$

$\frac{d{v}_8}{dt}=\frac{i_8}{C_8}-v_8\left(\frac{1}{Z{C}_8}+\frac{G_8}{C_8}\right)\text{.}$

The parameters are

R₁ = R₂ = R₃ = R₄ = R₅ = R₆ = R₇ = R₈ = 25 μΩ;

L₁ = L₃ = L₅ = L₇ = 1 mH, L₂ = L₄ = L₆ = L₈ = 10 mH;

C₁ = C₃ = C₅ = C₇ = 0.7 pF, C₂ = C₄ = C₆ = C₈ = 7 pF,

C₁₅ = C₃₇ = 0.35 pF, C₂₆ = C₄₈ = 3.5 pF;

G₁ = G₃ = G₅ = G₇ = 1/(5000 Ω),

G₂ = G₄ = G₆ = G₈ = 1/(500 Ω); L₁₅ = L₃₇ = 0.005 mH,

L₂₆ = L₄₈ = 0.01 mH.

Z is either 1 μΩ (short-circuit) or 1 MΩ (open-circuit). As input, assume the PWM voltage-step function v_s(t) (illustrated in Fig. E3.13.4).
Using Mathematica or MATLAB compute all state variables for the time period from t = t_calculate = 0 to 2.1 ms. Note that for some reason t_calculate must be larger than t_plot. Plot the voltages (v_s – v₁), (v₁ – v₅), (v₂ – v₆), (v₃ – v₇), and (v₄ – v₈).

b) For the detailed equivalent circuit of Fig. E3.13.2 establish all differential equations in a similar manner as has been done in part a. As input, assume a PWM voltage-step function v_s(t) (illustrated in Fig. E3.13.4).

Solution to Application Example 3.13

Solution #1 (Based on Mathematica)

a) Program list for short circuit with Z = 10^- 6Ω is presented in Table E3.13.1 and the cooresponding plots are shown in Figs. E3.13.5 to E3.13.10. Note that the computing time t = t_calculate = 2.1 ms must be larger than the plot time t = t_plot = 2 ms.
Program list for open circuit with Z = 10⁶Ω is presented in Table E3.13.2 and the cooresponding plots are shown in Figs. E3.13.11 to E3.13.15. Note that the computing time t = t_calculate = 2.1 ms must be larger than the plot time t = t_plot = 2 ms.

Table E3.13.1

Mathematica program list for Application Example 3.13 (part a) for short- circuit with Z = 10^- 6Ω

Hval = 10.01; Lval = 0; period = 200*10ˆ-6; duty = 0.5; Vs[t_]:=If[Mod[t,period] < duty*period,Hval,Lval]; Plot[Vs[t],{t,0,0.001},PlotRange- > All,AxesLabel - > {“t(s)”,“Vs(t)”}] R1 = 25*10ˆ-6;

eq1 = I1'[t]==-R1/L1*I1[t]-V1[t]/L1 + Vs[t]/L1; ic1 = I1[0]==0; eq2 = V1'[t]==I1[t]/C1-G1/C1*V1[t]-I2[t]/C1; ic2 = V1[0]==0; eq3 = I2'[t]==-R2/L2*I2[t]-V2[t]/L2 + V1[t]/L2; ic3 = I2[0]==0; eq4 = V2'[t]==I2[t]/C2-G2/C2*V2[t]-I3[t]/C2; ic4 = V2[0]==0; eq5 = I3'[t]==-R3/L3*I3[t]-V3[t]/L3 + V2[t]/L3; ic5 = I3[0]==0;

R2 = 25*10ˆ-6; R3 = 25*10ˆ-6; R4 = 25*10ˆ-6; R5 = 25*10ˆ-6; R6 = 25*10ˆ-6; R7 = 25*10ˆ-6; R8 = 25*10ˆ-6; L1 = 1*10ˆ-3; L3 = 1*10ˆ-3; L5 = 1*10ˆ-3; L7 = 1*10ˆ-3; L2 = 10*10ˆ-3; L4 = 10*10ˆ-3; L6 = 10*10ˆ-3; L8 = 10*10ˆ-3; L15 = 5*10ˆ-6; L37 = 5*10ˆ-6; L26 = 10*10ˆ-6; L48 = 10*10ˆ-6; C1 = .7*10ˆ-12; C3 = .7*10ˆ-12; C5 = .7*10ˆ-12; C7 = .7*10ˆ-12; C2 = 7*10ˆ-12; C4 = 7*10ˆ-12; C6 = 7*10ˆ-12; C8 = 7*10ˆ-12; C15 = .35*10ˆ-12; C37 = .35*10ˆ-12; C26 = 3.5*10ˆ-12; C48 = 3.5*10ˆ-12; G1 = 1/5000; G3 = 1/5000; G5 = 1/5000; G7 = 1/5000; G2 = 1/500; G4 = 1/500; G6 = 1/500; G8 = 1/500; Z = 1*10ˆ-6;

eq6 = V3'[t]==I3[t]/C3-G3/C3*V3[t]-I4[t]/C3; ic6 = V3[0]==0; eq7 = I4'[t]==-R4/L4*I4[t]-V4[t]/L4 + V3[t]/L4; ic7 = I4[0]==0; eq8 = V4'[t]==I4[t]/C4-G4/C4*V4[t]-I5[t]/C4; ic8 = V4[0]==0; eq9 = I5'[t]==-R5/L5*I5[t]-V5[t]/L5 + V4[t]/L5; ic9 = I5[0]==0; eq10 = V5'[t]==I5[t]/C5-G5/C5*V5[t]-I6[t]/C5; ic10 = V5[0]==0; eq11 = I6'[t]==-R6/L6*I6[t]-V6[t]/L6 + V5[t]/L6; ic11 = I6[0]==0; eq12 = V6'[t]==I6[t]/C6-G6/C6*V6[t]-I7[t]/C6; ic12 = V6[0]==0; eq13 = I7'[t]==-R7/L7*I7[t]-V7[t]/L7 + V6[t]/L7; ic13 = I7[0]==0; eq14 = V7'[t]==I7[t]/C7-G7/C7*V7[t]-I8[t]/C7; ic14 = V7[0]==0; eq15 = I8'[t]==−R8/L8*I8[t]/L8+V7[t]/L8; ic15 = I8[0]==0; eq16 = V8'[t]==I8[t]/C8-V8[t]*(1/(Z*C8) + G8/C8); ic16 = V8[0]==0; sol1 = NDSolve[{eq1,eq2,eq3,eq4,eq5,eq6,eq7, eq8,eq9,eq10,eq11,eq12,eq13,eq14,eq15,eq16, ic1,ic2,ic3,ic4,ic5,ic6,ic7,ic8,ic9,ic10,ic11,ic12, ic13,ic14,ic15,ic16},{I1[t],V1[t],I2[t],V2[t],I3[t], V3[t],I4[t],V4[t],I5[t],V5[t],I6[t],V6[t],I7[t],V7[t], I8[t],V8[t]},{t,0,0.0022},MaxSteps- > 100000]; Plot[Vs[t]-Evaluate[V1[t]/.sol1],{t,0,0.002}, AxesLabel- > {“Time”, “(Vs-V1) (V)”}] Plot[Evaluate[V1[t]/.sol1]-Evaluate[V5[t]/.sol1], {t,0,0.002},AxesLabel- > {“t(s)”, “(V1-V5) (V)”}] Plot[Evaluate[V2[t]/.sol1]-Evaluate[V6[t]/.sol1], {t,0,0.002},AxesLabel- > {“t(s)”, “(V2-V6) (V)”}] Plot[Evaluate[V3[t]/.sol1]-Evaluate[V7[t]/.sol1], {t,0,0.002},AxesLabel- > {“t(s)”, “(V3-V7) (V)”}] Plot[Evaluate[V4[t]/.sol1]-Evaluate[V8[t]/.sol1], {t,0,0.002},AxesLabel- > {“t(s)”, “(V4-V8) (V)”}]

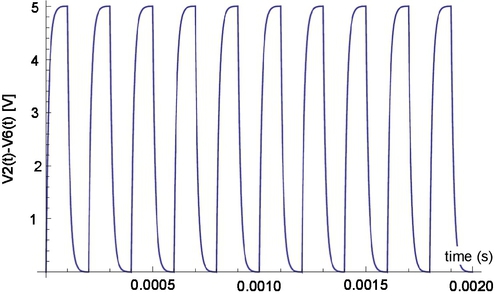
Table E3.13.2

Mathematica program list for Application Example 3.13 (part a) for open- circuit with Z = 10⁶Ω

Hval = 10.; Lval = 0; period = 200*10ˆ-6; duty = 0.5; Vs[t_]:=If[Mod[t,period] < duty*period,Hval,Lval]; Plot[Vs[t],{t,0,0.001},PlotRange- > All,AxesLabel - > {“t(s)”,“Vs(t)”}] R1 = 25*10ˆ-6; R2 = 25*10ˆ-6; R3 = 25*10ˆ-6; R4 = 25*10ˆ-6; R5 = 25*10ˆ-6; R6 = 25*10ˆ-6; R7 = 25*10ˆ-6; R8 = 25*10ˆ-6; L1 = 1*10ˆ-3; L3 = 1*10ˆ-3; L5 = 1*10ˆ-3; L7 = 1*10ˆ-3; L2 = 10*10ˆ-3; L4 = 10*10ˆ-3; L6 = 10*10ˆ-3; L8 = 10*10ˆ-3; L15 = 5*10ˆ-6; L37 = 5*10ˆ-6; L26 = 10*10ˆ-6; L48 = 10*10ˆ-6; C1 = .7*10ˆ-12; C3 = .7*10ˆ-12; C5 = .7*10ˆ-12; C7 = .7*10ˆ-12; C2 = 7*10ˆ-12; C4 = 7*10ˆ-12; C6 = 7*10ˆ-12; C8 = 7*10ˆ-12; C15 = .35*10ˆ-12; C37 = .35*10ˆ-12;

eq1 = I1'[t]==-R1/L1*I1[t]-V1[t]/L1 + Vs[t]/L1; ic1 = I1[0]==0; eq2 = V1'[t]==I1[t]/C1-G1/C1*V1[t]-I2[t]/C1; ic2 = V1[0]==0; eq3 = I2'[t]==-R2/L2*I2[t]-V2[t]/L2 + V1[t]/L2; ic3 = I2[0]==0; eq4 = V2'[t]==I2[t]/C2-G2/C2*V2[t]-I3[t]/C2; ic4 = V2[0]==0; eq5 = I3'[t]==-R3/L3*I3[t]-V3[t]/L3 + V2[t]/L3; ic5 = I3[0]==0; eq6 = V3'[t]==I3[t]/C3-G3/C3*V3[t]-I4[t]/C3; ic6 = V3[0]==0; eq7 = I4'[t]==-R4/L4*I4[t]-V4[t]/L4 + V3[t]/L4; ic7 = I4[0]==0; eq8 = V4'[t]==I4[t]/C4-G4/C4*V4[t]-I5[t]/C4; ic8 = V4[0]==0; eq9 = I5'[t]==-R5/L5*I5[t]-V5[t]/L5 + V4[t]/L5; ic9 = I5[0]==0; eq10 = V5'[t]==I5[t]/C5-G5/C5*V5[t]-I6[t]/C5; ic10 = V5[0]==0; eq11 = I6'[t]==-R6/L6*I6[t]-V6[t]/L6 + V5[t]/L6; ic11 = I6[0]==0; eq12 = V6'[t]==I6[t]/C6-G6/C6*V6[t]-I7[t]/C6; ic12 = V6[0]==0; eq13 = I7'[t]==-R7/L7*I7[t]-V7[t]/L7 + V6[t]/L7; ic13 = I7[0]==0; eq14 = V7'[t]==I7[t]/C7-G7/C7*V7[t]-I8[t]/C7; ic14 = V7[0]==0; eq15 = I8'[t]==-R8/L8*I8[t]-V8[t]/L8 + V7[t]/L8; ic15 = I8[0]==0; eq16 = V8'[t]==I8[t]/C8-V8[t]*(1/(Z*C8) + G8/C8); ic16 = V8[0]==0; sol1 = NDSolve[{eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8, eq9,eq10,eq11,eq12,eq13,eq14,eq15,eq16,ic1,ic2, ic3,ic4,ic5,ic6,ic7,ic8,ic9,ic10,ic11,ic12,ic13,ic14, ic15,ic16},{I1[t],V1[t],I2[t],V2[t],I3[t],V3[t],I4[t], V4[t],I5[t],V5[t],I6[t],V6[t],I7[t],V7[t],I8[t],V8[t]} ,{t,0,0.0022},MaxSteps- > 100000]; Plot[Vs[t]-Evaluate[V1[t]/.sol1],{t,0,0.002},

C26 = 3.5*10ˆ-12; C48 = 3.5*10ˆ-12; G1 = 1/5000; G3 = 1/5000; G5 = 1/5000; G7 = 1/5000; G2 = 1/500; G4 = 1/500; G6 = 1/500; G8 = 1/500; Z = 1*10ˆ6;

AxesLabel- > {“Time”, “(Vs-V1) (V)”}] Plot[Evaluate[V1[t]/.sol1]-Evaluate[V5[t]/.sol1], {t,0,0.002},AxesLabel- > {“t(s)”,“(V1-V5) (V)”}] Plot[Evaluate[V2[t]/.sol1]-Evaluate[V6[t]/.sol1], {t,0,0.002},AxesLabel- > {"t(s)","(V2-V6) (V)"}] Plot[Evaluate[V3[t]/.sol1]-Evaluate[V7[t]/.sol1], {t,0,0.002},AxesLabel- > {“t(s)”,“(V3-V7) (V)”}] Plot[Evaluate[V4[t]/.sol1]-Evaluate[V8[t]/.sol1], {t,0,0.002},AxesLabel- > {“t(s)”,“(V4-V8) (V)”}]

b) The detailed equivalent circuit (Fig. E3.13.2) generates about the same result as the simplified equivalent circuit (Fig. E3.13.3) and the results are therefore not given. Note, the state-variable equations of Eqs. E13-1 to E13-8 are still valid for the detailed equivalent circuit. However, the following four equations need to be added (assuming that the initial current through all the branches is zero):

$\frac{d{i}_{15}}{dt}=\frac{v_1}{L_{15}}-\frac{i_{15}}{L_{15}{C}_{15}}-\frac{v_5}{L_{15}}\text{,}$

  (E3.13-9)

$\frac{d{i}_{26}}{dt}=\frac{v_2}{L_{26}}-\frac{i_{26}}{L_{26}{C}_{26}}-\frac{v_6}{L_{26}}\text{,}$

  (E3.13-10)

$\frac{d{i}_{37}}{dt}=\frac{v_3}{L_{37}}-\frac{i_{37}}{L_{37}{C}_{37}}-\frac{v_7}{L_{37}}\text{,}$

  (E3.13-11)

$\frac{d{i}_{48}}{dt}=\frac{v_4}{L_{48}}-\frac{i_{48}}{L_{48}{C}_{48}}-\frac{v_8}{L_{48}}\text{.}$

  (E3.13-12)

Solution #2 (Based on MATLAB)

The results as obtained from Mathematica and Matlab are not exactly identical due to the different intergration algorithms used by both software programs, and the results are not given here due to space limitations.

3.11.2 Application Example 3.14: Calculation of Winding Stress Due to PMW Current-Source Inverters

Current ripples due to PWM current-source inverters cause voltage stress in windings of machines and transformers. The configuration of Fig. E3.14.1 represents a simple winding with two turns. Each winding can be represented by four segments having an inductance L_i, a resistance R_i, a capacitance to ground (frame) C_i, and some interturn capacitances C_ij and inductances L_ij. Figure E.3.14.2 represents a detailed equivalent circuit for the configuration of Fig. E3.14.1.

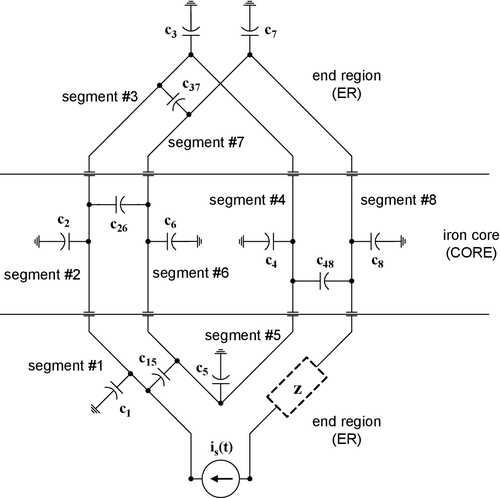
a) To simplify the analysis neglect the capacitances C_ij and the inductances L_ij. This leads to the circuit of Fig. E3.14.3, where the winding is fed by a PWM current source. One obtains the 15 differential equations of Eqs. E3.14-1 to E3.14-8a,b as listed below. In this case the current through L₁ is given (e.g., i_s(t)) and, therefore, there are only 15 differential equations, as compared with Application Example 3.13.

$\frac{d{v}_1}{dt}=\frac{i_s}{C_1}-\frac{G_1}{C_1}{v}_1-\frac{i_2}{C_1}\text{,}$

$\frac{d{i}_2}{dt}=-\frac{R_2}{L_2}{i}_2-\frac{v_2}{L_2}+\frac{v_1}{L_2}\text{,}$

$\frac{d{v}_2}{dt}=\frac{i_2}{C_2}-\frac{G_2}{C_2}{v}_2-\frac{i_3}{C_2}\text{,}$

$\frac{d{i}_3}{dt}=-\frac{R_3}{L_3}{i}_3-\frac{v_3}{L_3}+\frac{v_2}{L_3}\text{,}$

$\frac{d{v}_3}{dt}=\frac{i_3}{C_3}-\frac{G_3}{C_3}{v}_3-\frac{i_4}{C_3}\text{,}$

$\frac{d{i}_4}{dt}=-\frac{R_4}{L_4}{i}_4-\frac{v_4}{L_4}+\frac{v_3}{L_4}\text{,}$

$\frac{d{v}_4}{dt}=\frac{i_4}{C_4}-\frac{G_4}{C_4}{v}_4-\frac{i_5}{C_4}\text{,}$

$\frac{d{i}_5}{dt}=-\frac{R_5}{L_5}{i}_5-\frac{v_5}{L_5}+\frac{v_4}{L_5}\text{,}$

$\frac{d{v}_5}{dt}=\frac{i_5}{C_5}-\frac{G_5}{C_5}{v}_5-\frac{i_6}{C_5}\text{,}$

$\frac{d{i}_6}{dt}=-\frac{R_6}{L_6}{i}_6-\frac{v_6}{L_6}+\frac{v_5}{L_6}\text{,}$

$\frac{d{v}_6}{dt}=\frac{i_6}{C_6}-\frac{G_6}{C_6}{v}_6-\frac{i_7}{C_6}\text{,}$

$\frac{d{i}_7}{dt}=-\frac{R_7}{L_7}{i}_7-\frac{v_7}{L_7}+\frac{v_6}{L_7}\text{,}$

$\frac{d{v}_7}{dt}=\frac{i_7}{C_7}-\frac{G_7}{C_7}{v}_7-\frac{i_8}{C_7}\text{,}$

$\frac{d{i}_8}{dt}=-\frac{R_8}{L_8}{i}_8-\frac{v_8}{L_8}+\frac{v_7}{L_8}\text{,}$

$\frac{d{v}_8}{dt}=\frac{i_8}{C_8}-v_8\left(\frac{1}{Z{C}_8}+\frac{G_8}{C_8}\right)\text{.}$

The parameters are

R₁ = R₂ = R₃ = R₄ = R₅ = R₆ = R₇ = R₈ = 25 μΩ;

L₁ = L₃ = L₅ = L₇ = 1 mH, L₂ = L₄ = L₆ = L₈ = 10 mH;

C₁ = C₃ = C₅ = C₇ = 0.7 pF, C₂ = C₄ = C₆ = C₈ = 7 pF,

C₁₅ = C₃₇ = 0.35 pF, C₂₆ = C₄₈ = 3.5 pF;

G₁ = G₃ = G₅ = G₇ = 1/(5000 Ω),

G₂ = G₄ = G₆ = G₈ = 1/(500 Ω); and

L₁₅ = L₃₇ = 0.005 mH, L₂₆ = L₄₈ = 0.01 mH.

Z is either 1 μΩ (short-circuit) or 1 MΩ (open-circuit). Assume a PWM current-step function i_s(t) as indicated in Fig. E3.14.4.

b) For the simplified equivalent circuit using Mathematica compute all state variables during the time period from t = t_calculate = 0 to 2.1 ms at rise times of t_rise = 5 μs and 75 μs. Plot the current i_s (t) for 1 ms and voltages (v₁ – v₅), (v₂ – v₆), (v₃ – v₇), and (v₄ – v₈) for t_plot = 2 ms.

Solution to Application Example 3.14

To demonstrate the sensitivity of the induced voltage stress as a function of the rise time of the current ripple, a rise time of 5 μs has been assumed first and the results based on Table E3.14.1 are plotted in Figs. E3.14.5 to E3.14.9 for Z = 10^- 6Ω, that is the considered winding is short-circuited. Note, the voltage across capacitance C₁₅ (that is, the voltage between the first turn and the second turn at the end region (ER)) is very large. For trise = 75 μs at Z =10^- 6Ω the voltage stress is smaller (see Figs. E3.14.10 to E3.14.14).

The voltage stresses at open circuit (Z = 10⁶ Ω) at a rise time of t_rise =15 μs and 75 μs are similar to those of Figures E3.14.5 to E3.14.14.

3.12.1 Conventional Harmonic Model of an Induction Motor

Figures 3.3 and 3.25 represent the fundamental and harmonic per-phase equivalent circuits of a three-phase induction motor, respectively, which are used for the calculation of the steady-state performance. The rotor parameters may consist of the equivalent rotor impedance taking into account the cross-path resistance of the rotor winding, which is frequency dependent because of the skin effect in the rotor bars. The steady-state performance is calculated by using the method of superposition based on Figs. 3.3 and 3.25. In general, for the usual operating speed regions, the fundamental slip is very small and, therefore, the harmonic slip, s_h, is close to unity.

3.12.2 Modified Conventional Harmonic Model of an Induction Motor

In order to improve the loss prediction of the conventional harmonic equivalent circuit of induction machines (Fig. 3.25), the core loss and stray-core losses associated with high-frequency leakage fluxes are taken into account. Stray-load losses in induction machines are considered to be important – due to leakage – when induction machines are supplied by nonsinusoidal voltage or current sources. This phenomenon can be accounted for by a modified loss model, as shown in Fig. 3.40 [79].

3.12.3 Simplified Conventional Harmonic Model of an Induction Motor

As the mechanical speed is very close to the synchronous speed, the rotor slip with respect to the harmonic mmfs will be close to unity (e.g., about 6/5 and 6/7 for the 5th and 7th harmonics, respectively). Therefore, the resistance (1 – s_h)R′_r/s_h will be negligibly small in the harmonic model of Fig. 3.25, and the equivalent harmonic circuit may be reduced to that of Fig. 3.41. Only the winding resistances and the leakage inductances are included; the magnetizing branches are ignored because the harmonic voltages can be assumed to be relatively small, and at harmonic frequencies the core-flux density is small as well as compared with fundamental flux density. It should be noted that the winding resistances and leakage inductances are frequency dependent.

3.12.4 Spectral-Based Harmonic Model of an Induction Machine with Time and Space Harmonics

Figure 3.42 shows a harmonic equivalent circuit of an induction machine that models both time and space harmonics [81]. The three windings may or may not be balanced as each phase has its own per phase resistance R_equj, reactance X_equj, and speed-dependent complex electromagnetic force emf Ẽ_j (where j = 1, 2, 3 represents the phase number). To account for the core losses, two resistances in parallel are added to each phase: R_c1 representing the portion of losses that depends only on phase voltages and (ω_b/ω_s)R_c2 representing losses that depend on the frequency and voltage of the stator (ω_b is the rated stator frequency whereas ω_s is the actual stator frequency).

To account for space-harmonic effects, the spectral approach modeling technique is used. This concept combines effects of time harmonics (from the input power supply) and space harmonics (from machine windings and magnetic circuits), bearing in mind that no symmetrical components exist in both quantities.

The equivalent circuit of Fig. 3.42 has several branches (excluding the fundamental and the core losses), where each branch per phase is associated with one harmonic of the power supply (impedance) or one frequency for the space distribution (current source). To evaluate various parameters, the spectral analysis of both time-domain stator voltages and currents are required. The conventional blocked-rotor, no-load, and loaded shaft tests can be performed at fundamental frequency to evaluate phase resistance R_equj, reactance X_equj, complex emf Ẽ_j, R_c1, and R_c2.

The harmonic stator voltage ($\tilde{\mathit{V}}$_fij) and current (Ĩ_fij) with their respective magnitudes and phase angles need to be measured to determine harmonic impedances (e.g., R_fij + jX_fij is the ratio of the two phasors).

For the current sources coming from the space harmonics, one has to differentiate between power supply harmonics and space harmonics and those which are solely space-harmonic related. This can be done using a blocked-rotor test or a long-time starting test (with the primary objective of obtaining data at zero speed). Voltage and current measurements in the time domain allow the evaluation of the effects only related to the power supply harmonics in the frequency domain. Determination of the space-harmonics effects is made possible by utilizing the principle of superposition in steady state at a nonzero speed.

In the model of Fig. 3.42:

• Effects of both time and space harmonics are included;

• R_fij + jX_fij =$\tilde{\mathit{V}}$_fij/Ĩ_fij originates from phase voltage time harmonics (fi is the ith harmonic);

• Ĩ_fkj originates from the space harmonics (subscript fk is used for space harmonics);

• The skin effect is ignored, but could be easily included; and

• Core losses related to power supply harmonics except the fundamental are included in the harmonic circuit.

To introduce space harmonics into the model, current sources with the phasor notation Ĩ_fkj are used which are only linked to the load condition and, as a result, to the speed of the rotor. In most cases, the space-harmonics frequency fk is also a multiple of the power supply frequency f_s. It is understood that the space harmonics will affect electromagnetic torque calculations, which is not shown in the equivalent circuit.

Details of this equivalent circuit are presented in reference [81].

Figure P3.1a,b illustrates the torque–speed characteristics of a 10 kW three-phase induction motor with different rotor slot skewing with load torques T_L1, T_L2, and T_L3. Comment on the steady-state stability of the equilibrium points A, B, C, D, E, F, G, H, I, and J in Fig. P3.1a and A, B, C, D, and E in Fig. P3.1b.

Problem 3.2: Phasor Diagram of Induction Machine at Fundamental Frequency and Steady-State Operation

Draw the phasor diagram for the equivalent circuit of Fig. P3.2. You may use the consumer reference system.

Problem 3.3: Analysis of an Induction Generator for a Wind-Power Plant

A P_out = 3.5 MW, V_L-L = 2400 V, f = 60 Hz, p = 12 poles, n_m-generator = 618 rpm, Y-connected squirrel-cage wind-power induction generator has the following parameters per phase referred to the stator: R_S = 0.1 Ω, X_S = 0.5 Ω, X_m → ∞ (that is, X_m can be ignored), R′_r = 0.05 Ω, and X′_r = 0.2 Ω. You may use the equivalent circuit of Fig. P3.2 with X_m and R_fe large so that they can be ignored. Calculate:

a) Synchronous speed n_S in rpm.

b) Synchronous angular velocity ω_S in rad/s.

c) Slip s.

d) Rotor current Ĩ_r′.

e) (Electrical) generating torque T_gen.

f) Slip s_m where the maximum torque occurs.

g) Maximum torque T_max in generation region.

Problem 3.4: E/f Control of a Squirrel-Cage Induction Motor [93]

The induction machine of Problem 3.3 is now used as a motor at n_m-motor = 582 rpm. You may use the equivalent circuit of Fig. P3.2 with X_m and R_fe large so that they can be ignored. Calculate for E/f control:

a) Induced voltage Ẽ_rated.

b) Electrical torque T_rated.

c) The frequency f_new at n_m-new = 300 rpm, and T_rated.

d) The new slip s_new.

Problem 3.5: V/f Control of a Squirrel-Cage Induction Motor [93]

The induction machine of Problem 3.3 is now used as a motor at n_m-motor = 582 rpm. You may use the equivalent circuit of Fig. P3.2 with X_m and R_fe large so that they can be ignored. Calculate for V/f control:

a) Electrical torque T_rated.

b) The new slip s_new.

c) The frequency f_new at n_m-new = 300 rpm, and T_rated.

Problem 3.6: Steady-State Operation at Undervoltage

A P_out = 100 hp, V_{L-L_rat} = 480 V, f = 60 Hz, p = 6 pole three-phase induction motor runs at full load and rated voltage with a slip of 3%. Under conditions of stress on the power supply system, the line-to-line voltage drops to V_{L-L_low} = 450 V. If the load is of the constant torque type, compute for the lower voltage:

a) The slip s_low (use small-slip approximation).

b) The shaft speed n_{m_low} in rpm.

c) The output power P_{out_low}.

d) The rotor copper loss P_{cur_low} = I_r′²R_r′ in terms of the rated rotor copper loss at rated voltage.

Problem 3.7: Steady-State Operation at Overvoltage

Repeat Problem 3.6 for the condition when the line-to-line voltage of the power supply system increases to V_{L-L_high} = 500 V.

Problem 3.8: Steady-State Operation at Undervoltage and Under-Frequency

A P_{out_rat} = 100 hp, V_{L-L_rat} = 480 V, f = 60 Hz, p = 6 pole three-phase induction motor runs at full load and rated voltage and frequency with a slip of 3%. Under conditions of stress on the power supply system the terminal voltage and the frequency drop to V_{L-L_low} = 450 V and f_low = 59.5 Hz, respectively. If the load is of the constant torque type, compute for the lower voltage and frequency:

a) The slip (use small-slip approximation).

b) The shaft speed in rpm.

c) The hp output.

d) The rotor copper loss P_{cur_low} = I_r′²R_r′ in terms of the rated rotor copper loss at rated frequency and voltage.

Problem 3.9: Steady-State Operation at Overvoltage and Over-Frequency

A P_{out_rat} = 100 hp, V_{L-L_rat} = 480 V, f = 60 Hz, p = 6 pole three-phase induction motor runs at full load and rated voltage and frequency with a slip of 3%. Assume the terminal voltage and the frequency increase to V_{L-L_high} = 500 V and f_high = 60.5 Hz, respectively. If the load is of the constant torque type, compute for the lower voltage and frequency:

a) The slip (use small-slip approximation).

b) The shaft speed in rpm.

c) The hp output.

d) The rotor copper loss P_{cur_ high} = I_r′²R_r′ in terms of the rated rotor copper loss at rated frequency and voltage.

Problem 3.10: Calculation of the Maximum Critical Speeds n_mcritical^motoring and n_mcritical^regeneration for Motoring and Regeneration, Respectively [93]

A V_{L-L_rat} = 480 V, f_rat = 60 Hz, n_mrat = 1760 rpm, 4-pole, Y-connected squirrel-cage induction machine has the following parameters per phase referred to the stator: R_S = 0.2 Ω, X_S = 0.5 Ω, X_m = 20 Ω, R′_r = 0.1 Ω, X′_r = 0.8 Ω. Use the equivalent circuit of Fig. P3.10.1.

A hybrid car employs the induction machine with the above-mentioned parameters for the electrical part of the drive.

a) Are the characteristics of Figure P3.10.2 (for a = f/f_rated< 1) either E/f control or V/f control?

b) Compute the rated electrical torque T_rat , the rated angular velocity ω_mrat and the rated output power P_rat (see operating point Q₁ of Figure P3.10.2).

c) Calculate the maximum critical motoring speed n_mcritical^motoring, whereby rated output power (P_rat = T_rat · ω_mrat) is delivered by the machine at the shaft (see operating point Q₂ of Fig. P3.10.2).

d) Calculate the maximum critical speed n_mcritical^regeneration, whereby rated power is absorbed at the shaft by the machine (see operating point Q₃ of Fig. P3.10.2).

e) In order to increase the critical motoring speed to about 3 times the rated speed n_mrat an engineer proposes to decrease X_s and X′_r by a factor of two. Will this accomplish the desired speed increase? Note that the resistances R_s and R′_r are so small that no significant speed increase can be expected by changing them.

Problem 3.11: Torque Characteristic of Induction Machine with Fundamental and Subharmonic Fields

The equivalent circuit of a voltage-source-fed induction motor is shown in Fig. 3.38. The fundamental angular frequency of the voltage source is ω₁ and the time-harmonic angular frequency is hω₁ (caused by imperfections of the voltage-source inverter).

The parameters of the three-phase induction motor are as follows: V_L-L = 460 V, Y-connected, p = 2 poles, n_rated = 3528 rpm, f = 60 Hz, R_s = 1 Ω, ω₁L_sℓ = 2 Ω, ω₁L_m = ∞ (you may neglect the magnetizing branch), R′_r = 1 Ω, ω₁L′_rℓ = 2 Ω.

a) Compute a few points (e.g., T_e1(s₁ = 0), T_e1(s₁ = s_1max +), T_e1(s₁ = s_1max–),T_e1(s₁ = 1.0)) and sketch the fundamental torque characteristic T_e1 = f(s₁) in Nm, where s₁ is the slip of the rotor with respect to the fundamental positively rotating (forward rotating, positive sequence) field.

b) Provided a negatively rotating (backward rotating, negative sequence) voltage time subharmonic of 30 Hz (h = 0.5) is present with a magnitude of V_s0.5/V_s1 = 0.10 compute a few points (e.g., T_e0.5(s_0.5 = 0), Te_0.5(s_0.5 = s_0.5max +), T_e0.5(s_0.5 = s_0.5max–), T_e0.5(s_0.5 = 1.0)) of this subharmonic torque characteristic T_e0.5 = f(s_0.5) in Nm.

c) Sketch the subharmonic torque characteristic T_e0.5 = f(s_0.5) in Nm.

d) Sketch the total torque characteristics (T_e1 + T_e0.5) = f(s₁) in Nm.

e) What is the starting torque (at s₁ = 1) without and with this (h = 0.5) time subharmonic?

Problem 3.12: Voltage Stress due to Current Ripples in Stator Windings of an Induction Motor Fed by a Current-Source Inverter Through a Cable of 10 m Length

Current ripples due to PWM current-source inverters cause voltage stress in windings of machines. The configuration of Fig. E3.14.1 represents the first two turns of the winding of an induction motor. Each turn can be represented by four segments having an inductance L_i, a resistance R_i, a capacitance to ground (frame) C_i, and some interturn capacitances C_ij and inductances L_ij. Figure E.3.14.2 represents a detailed equivalent circuit for the configuration of Fig. E3.14.1. To simplify the analysis neglect the capacitances C_ij and the inductances L_ij. This leads to the circuit in Fig. E3.14.3, where the winding is fed by a PWM current source. One obtains the 15 differential equations as listed below.

$\frac{d{v}_1}{dt}=\frac{i_s}{C_1}-\frac{G_1}{C_1}{v}_1-\frac{i_2}{C_1}\text{,}$

$\frac{d{i}_2}{dt}=-\frac{R_2}{L_2}{i}_2-\frac{v_2}{L_2}+\frac{v_1}{L_2}\text{,}$