CHAPTER 4
CONFIDENCE INTERVALS
4.1 INTRODUCTION
![]() Table 4.1 contains a discrete population of 100 values. The mean (μ) and variance (σ2) of that population are 26.1 and 17.5, respectively. By randomly selecting 10 values from Table 4.1, an estimate for the mean and variance of the population can be determined. However, it should not be expected that these estimates (
Table 4.1 contains a discrete population of 100 values. The mean (μ) and variance (σ2) of that population are 26.1 and 17.5, respectively. By randomly selecting 10 values from Table 4.1, an estimate for the mean and variance of the population can be determined. However, it should not be expected that these estimates (![]() and S2) would exactly match the mean and variance of the population. Sample sets of 10-values each could continue to be selected from the population to determine additional estimates for the mean and variance of the population. However, it is just as unlikely that these additional values would match those obtained from either the population or the first sample set.
and S2) would exactly match the mean and variance of the population. Sample sets of 10-values each could continue to be selected from the population to determine additional estimates for the mean and variance of the population. However, it is just as unlikely that these additional values would match those obtained from either the population or the first sample set.
TABLE 4.1 Population of 100 Values
| 18.2 | 26.4 | 20.1 | 29.9 | 29.8 | 26.6 | 26.2 |
| 25.7 | 25.2 | 26.3 | 26.7 | 30.6 | 22.6 | 22.3 |
| 30.0 | 26.5 | 28.1 | 25.6 | 20.3 | 35.5 | 22.9 |
| 30.7 | 32.2 | 22.2 | 29.2 | 26.1 | 26.8 | 25.3 |
| 24.3 | 24.4 | 29.0 | 25.0 | 29.9 | 25.2 | 20.8 |
| 29.0 | 21.9 | 25.4 | 27.3 | 23.4 | 38.2 | 22.6 |
| 28.0 | 24.0 | 19.4 | 27.0 | 32.0 | 27.3 | 15.3 |
| 26.5 | 31.5 | 28.0 | 22.4 | 23.4 | 21.2 | 27.7 |
| 27.1 | 27.0 | 25.2 | 24.0 | 24.5 | 23.8 | 28.2 |
| 26.8 | 27.7 | 39.8 | 19.8 | 29.3 | 28.5 | 24.7 |
| 22.0 | 18.4 | 26.4 | 24.2 | 29.9 | 21.8 | 36.0 |
| 21.3 | 28.8 | 22.8 | 28.5 | 30.9 | 19.1 | 28.1 |
| 30.3 | 26.5 | 26.9 | 26.6 | 28.2 | 24.2 | 25.5 |
| 30.2 | 18.9 | 28.9 | 27.6 | 19.6 | 27.9 | 24.9 |
| 21.3 | 26.7 |
As the sample size is increased, the mean and variance of the sample should approach the values of the population. In fact, as the sample size becomes very, very large, the mean and variance of the samples should be close to those of the population. This procedure was done for various sample sizes starting at 10 values and increasing the sample by 10 values with the results shown in Table 4.2. Note that the value computed for the mean of the sample approaches the value of the population as the sample size is increased. Similarly, the value computed for the variance of the sample also tends to approach the value of the population as the sample size is increased.
TABLE 4.2 Increasing Sample Sizes
| No. | S2 | |
| 10 | 26.9 | 28.1 |
| 20 | 25.9 | 21.9 |
| 30 | 25.9 | 20.0 |
| 40 | 26.5 | 18.6 |
| 50 | 26.6 | 20.0 |
| 60 | 26.4 | 17.6 |
| 70 | 26.3 | 17.1 |
| 80 | 26.3 | 18.4 |
| 90 | 26.3 | 17.8 |
| 100 | 26.1 | 17.5 |
Since the mean of a sample set ![]() and its variance S2 are computed from random variables, they are also random variables. This means that even if the size of the sample is kept constant, varying values for the mean and variance can be estimated from the samples with greater confidence given to larger samples. Also, it can be concluded that the values computed from a sample also contain errors. To illustrate this, an experiment was run for four randomly selected sets of 10 values from Table 4.1. Table 4.3 lists these samples, their means, and variances. Notice the variation in the computed values for the four sets. As discussed above, this variation is expected.
and its variance S2 are computed from random variables, they are also random variables. This means that even if the size of the sample is kept constant, varying values for the mean and variance can be estimated from the samples with greater confidence given to larger samples. Also, it can be concluded that the values computed from a sample also contain errors. To illustrate this, an experiment was run for four randomly selected sets of 10 values from Table 4.1. Table 4.3 lists these samples, their means, and variances. Notice the variation in the computed values for the four sets. As discussed above, this variation is expected.
TABLE 4.3 Random Sample Sets from Population
| Set 1: 29.9, 18.2, 30.7, 24.4, 36.0, 25.6, 26.5, 29.9, 19.6, 27.9 | S2 = 28.1 | |
| Set 2: 26.9, 28.1, 29.2, 26.2, 30.0, 27.1, 26.5, 30.6, 28.5, 25.5 | S2 = 2.9 | |
| Set 3: 32.2, 22.2, 23.4, 27.9, 27.0, 28.9, 22.6, 27.7, 30.6, 26.9 | S2 = 10.9 | |
| Set 4: 24.2, 36.0, 18.2, 24.3, 24.0, 28.9, 28.8, 30.2, 28.1, 29.0 | S2 = 23.0 |
Fluctuations in the computed means and variances from varying sample sets raises questions about the ability of these values to reliably estimate the population values. For example, a higher confidence is likely to be placed on a sample set with a small variance than on one with a large variance. Thus in Table 4.3, because of its small variance, one is more likely to believe that the mean of the second sample set is a more reliable estimate for the mean of the population than the others. In reality this is not the case since the means of the other three sets are actually closer to the population mean of 26.1.
As noted earlier, the size of the sample should be also considered when determining the reliability of a computed mean or variance. If the mean were computed from a sample of five values and another computed from a sample of 30, then more confidence is likely to be placed on the values derived from the larger sample set than the smaller one, even if both sample sets have the same mean and standard deviation.
In statistics, this relationship between the sample sets, the number of samples, and the values computed for the means and variances is part of sampling distribution theory. This theory recognizes that estimates for the mean and variance do vary from sample to sample. Estimators are the functions used to compute these estimates. Examples of estimator functions are Equations (2.1) and (2.5) that are used to compute estimates of the mean and variance for a population, respectively. As demonstrated and discussed, these estimates vary from sample to sample and thus have their own population distributions. In Section 4.2, three distributions are defined that are used for describing or quantifying the reliability of mean and variance estimates. By applying these distributions, statements can be written about the reliability of the computed estimates at any given level of confidence. In other words, a range called the confidence interval can be determined within which the population mean and population variance can be expected to fall for varying levels of probability.
4.2 DISTRIBUTIONS USED IN SAMPLING THEORY
4.2.1 χ2 Distribution
The chi-squared distribution, symbolized as χ2, compares the relationship between the population variance and the variance of a sample set based on the number of redundancies in the sample. It was first published by Karl Pearson in 1900. If a random sample of n observations, y1, y2,…, yn, is selected from a population that has a normal distribution with mean μ and variance σ2, then by definition, the χ2 sampling distribution is
where v is the number of degrees of freedom in the sample, and the other terms are as defined previously.
A plot of the distribution is shown in Figure 4.1. The number of redundancies (degrees of freedom) in sample set statistics such as those for the mean or variance are v = n − 1. In later chapters, on least squares it will be shown that the number of redundancies is based on the number of independent observations and unknown parameters. In the case of the mean, one observation is necessary to determine the mean, thus leaving n − 1 values as redundant observations. Table D.2 is a tabulation of χ2 distribution curves for various degrees of freedom from 1 to 120. To find the area under the upper tail of the curve (right side shown shaded in Figure 4.1) starting at some specific χ2 value and going to infinity (∞), intersect the row corresponding to the appropriate degrees of freedom, v, with the column corresponding to the desired area under the curve. For example, to find the specific χ2 value relating to 1% (α = 0.010) of the area under a curve having 10 degrees of freedom, intersect the row headed by 10 with the column headed by 0.010 and find a χ2 value of 23.21. This means that 1% of the area under this curve lies in the upper tail of this curve between the values of 23.21 and ∞.

FIGURE 4.1 χ2 distribution.
Due to the asymmetric nature of the distribution, the percentage points1 (α) of the lower tail (left side of the curve) must be computed from those tabulated for the upper tail. A specific area under the left side (lower tail) of the curve starting at zero and going to some specific χ2 value is found by subtracting the tabulated α (right-side area) from 1. This can be done since Table D.2 lists α (areas) starting at the χ2 value and going to ![]() , and the total area under the curve is 1. For example, if there are 10 degrees of freedom and the χ2 value relating to 1% of the area under the left side of the curve is needed, the row corresponding to v equal to 10 is intersected with the column headed by α = 0.990 (1 − 0.010), and a value of 2.56 is obtained. This means that 1% of the area under the curve occurs from 0 to 2.56.
, and the total area under the curve is 1. For example, if there are 10 degrees of freedom and the χ2 value relating to 1% of the area under the left side of the curve is needed, the row corresponding to v equal to 10 is intersected with the column headed by α = 0.990 (1 − 0.010), and a value of 2.56 is obtained. This means that 1% of the area under the curve occurs from 0 to 2.56.
The χ2 distribution is used in sampling statistics to determine the range in which the variance of the population can be expected to occur based on (1) some specified percentage probability; (2) the variance of a sample set; and (3) the number degrees of freedom in the sample. In an example given in Section 4.6, this distribution is used to construct probability statements about the variance of the population being in a range centered about the variance S2 of a sample having v degrees of freedom. In Section 5.3 a statistical test is presented using the χ2 distribution to check if the variance of a sample is a valid estimate for the population variance.
4.2.2 Student's t Distribution
The t distribution was developed in 1905 by William Seally Gosset, a chemist at Guinness brewery in Dublin, Ireland. At the time, he used the pseudonym of Student, and thus the distribution is sometimes called Student's t distribution. The distribution is used to compare a population mean with the mean of a sample set based on the number of redundancies (v) in the sample set. It is similar to the normal distribution (discussed in Chapter 3), except that the normal distribution applies to an entire population, whereas the t distribution applies to a sample set of the population. This distribution is preferred over the normal distribution when the sample contains fewer than 30 values. Thus, it is an important distribution in analyzing surveying data.
If z is a standard normal random variable as defined in Section 3.4, χ2 is a chi-squared random variable with v degrees of freedom, and z and χ2 are both independent variables, then by definition
The t values for selected upper-tail percentage points (shaded area in Figure 4.2) versus the t distributions with various degrees of freedom v are listed in Table D.3. For specific degrees of freedom (v) and percentage points (α), the table lists specific t values that correspond to the areas α under the curve between the tabulated t values and ![]() . Similar to the normal distribution, the t distribution is symmetric. Generally in statistics only percentage points in the range 0.0005 to 0.4 are necessary since the curve is symmetric. These t values are tabulated in Table D.3. To find the t value relating to α = 0.01 for a curve developed with 10 degrees of freedom (v = 10), intersect the row corresponding to v = 10 with the row corresponding to α = 0.01. At this intersection the t value of 2.764 is obtained. This means that 1% (α = 0.01) of the area exists under the t distribution curve having 10 degrees of freedom in the interval between 2.764 and
. Similar to the normal distribution, the t distribution is symmetric. Generally in statistics only percentage points in the range 0.0005 to 0.4 are necessary since the curve is symmetric. These t values are tabulated in Table D.3. To find the t value relating to α = 0.01 for a curve developed with 10 degrees of freedom (v = 10), intersect the row corresponding to v = 10 with the row corresponding to α = 0.01. At this intersection the t value of 2.764 is obtained. This means that 1% (α = 0.01) of the area exists under the t distribution curve having 10 degrees of freedom in the interval between 2.764 and ![]() . Due to the symmetry of this curve, it can also be stated that 1% (α = 0.01) of the area under the curve developed for 10 degrees of freedom also lies between −∞ and −2.764.
. Due to the symmetry of this curve, it can also be stated that 1% (α = 0.01) of the area under the curve developed for 10 degrees of freedom also lies between −∞ and −2.764.

FIGURE 4.2 t distribution.
As described in Section 4.3, this distribution is used to construct confidence intervals for the population mean (μ) based on the mean (![]() ) and variance (S2) of a sample set and the degrees of freedom (v). An example in that section illustrates the procedure. Furthermore, in Section 5.3 it is shown that this distribution can be used to determine if the sample mean is a good estimate for the population mean.
) and variance (S2) of a sample set and the degrees of freedom (v). An example in that section illustrates the procedure. Furthermore, in Section 5.3 it is shown that this distribution can be used to determine if the sample mean is a good estimate for the population mean.
4.2.3 F Distribution
This distribution is used when comparing the computed variances from two sample sets. If ![]() and
and ![]() are two chi-squared random variables with v1 and v2 degrees of freedom, respectively, and both variables are independent, then by definition
are two chi-squared random variables with v1 and v2 degrees of freedom, respectively, and both variables are independent, then by definition
The distribution was first tabulated by George Snedecor as an aid for Ronald A. Fisher's analysis of variance. Fisher developed the statistic initially as the variance ratio in the 1920s.
Various percentage points (areas under the upper tail of the curve shown shaded in Figure 4.3) of the F distribution are tabulated in Table D.4. Notice that this distribution has v1 numerator degrees of freedom and v2 denominator degrees of freedom, which correspond to the two sample sets. Thus, unlike the χ2 and t distributions each desired α percentage point must be represented in a separate table. In Appendix D, tables for the more commonly used values of α (0.20, 0.10, 0.05, 0.025, 0.01, 0.005, and 0.001) are listed.

FIGURE 4.3 F distribution.
To illustrate the use of the tables, suppose that the F value for 1% area under the upper tail of the curve is needed. Also assume that 5 is the numerator degrees of freedom relating to S1, and 10 is the denominator degrees of freedom relating to S2. In this example, α equals 0.01 and thus the F table in Table D.4 that is written for α = 0.01 must be used. In that table, intersect the row headed by v2 equal to 10 with the column headed by v1 equal to 5, and find the F value of 5.64. This means that 1% of the area under the curve constructed using these degrees of freedom lies in the region going from 5.64 to +∞.
To determine the area in the lower tail of this distribution, use the following functional relationship.
The critical F value for the data in the previous paragraph (v1 equal to 5 and v2 equal to 10) with α equal to 0.99 (0.01 in the lower tail) is determined by going to the intersection of the row headed by 5 with the column headed by 10 on the α equal to 0.01 page. The intersection is at F equal to 2.19. According to Equation (4.4) the critical F0.99,5,10 is ![]() . Thus, 1% of the area is under the F distribution curve going from zero to 0.457.
. Thus, 1% of the area is under the F distribution curve going from zero to 0.457.
The F distribution is used to answer the question on whether two sample sets come from the same population. For example, suppose that two samples have variances of ![]() and
and ![]() . If these two sample variances represent the same population variance, the ratio of their population variances
. If these two sample variances represent the same population variance, the ratio of their population variances ![]() should equal 1 (i.e.,
should equal 1 (i.e., ![]() ). As discussed in Section 4.7, this distribution enables confidence intervals to be established for the ratio of the population variances. Also, as discussed in Section 5.4, the distribution can be used to test whether the ratio of the two variances is statistically equal to 1.
). As discussed in Section 4.7, this distribution enables confidence intervals to be established for the ratio of the population variances. Also, as discussed in Section 5.4, the distribution can be used to test whether the ratio of the two variances is statistically equal to 1.
4.3 CONFIDENCE INTERVAL FOR THE MEAN: T STATISTIC
![]() In Chapter 3, the standard normal distribution was used to predict the range in which the mean of a population may exist. This was based on the mean and standard deviation for a sample set. However, as noted previously, the normal distribution is based on an entire population, and as was demonstrated, variations from the normal distribution are expected from sample sets having a small number of values. From this expectation, the t distribution was developed. As is demonstrated later in this section by an example, the t distribution (in Table D.3) for samples having an infinite number of values uses the same t values as those listed in Table 3.2 for the normal distribution. It is generally accepted that when the number of observations is greater than about 30, the values in Table 3.2 are valid for constructing intervals about the population mean. However, when the sample set have less than 30 values, a t value from the t distribution should be used to construct the confidence interval for the population mean.
In Chapter 3, the standard normal distribution was used to predict the range in which the mean of a population may exist. This was based on the mean and standard deviation for a sample set. However, as noted previously, the normal distribution is based on an entire population, and as was demonstrated, variations from the normal distribution are expected from sample sets having a small number of values. From this expectation, the t distribution was developed. As is demonstrated later in this section by an example, the t distribution (in Table D.3) for samples having an infinite number of values uses the same t values as those listed in Table 3.2 for the normal distribution. It is generally accepted that when the number of observations is greater than about 30, the values in Table 3.2 are valid for constructing intervals about the population mean. However, when the sample set have less than 30 values, a t value from the t distribution should be used to construct the confidence interval for the population mean.
To derive an expression for a confidence interval of the population mean, a sample mean ![]() is computed from a sample set of a normally distributed population having a mean of μ and variance of the mean of σ2/n. Let
is computed from a sample set of a normally distributed population having a mean of μ and variance of the mean of σ2/n. Let ![]() be a normal random variable. Substituting it and Equation (4.1) into Equation (4.2) yields
be a normal random variable. Substituting it and Equation (4.1) into Equation (4.2) yields
To compute a confidence interval for the population mean (μ) given a sample set mean and variance, it is necessary to determine the area of a (1 − α) region. For example in a 95% confidence interval (unshaded area in Figure 4.4), center the percentage point of 0.95 on the t distribution. This leaves 0.025 in each of the upper- and lower-tail areas (shaded areas in Figure 4.4). The t value that locates an α/2 area in both the upper and lower tails of the distribution is given in Table D.3 as tα/2,v. For sample sets having a mean of and variance of S2, the correct probability statement to locate this area is

FIGURE 4.4 tα/2 plot.
Substituting Equation (4.5) into Equation (a) yields

which after rearranging yields
Thus, given ![]() , tα/2,v, n, and S, it is seen from Equation (4.6) that a (1 − α) probable error interval for the population mean μ is computed as
, tα/2,v, n, and S, it is seen from Equation (4.6) that a (1 − α) probable error interval for the population mean μ is computed as
where tα/2 is the critical t value from the t distribution based on v degrees of freedom and α/2 percentage points.
The following example illustrates the use of Equation (4.7) and Table D.3 for determining the 95% confidence interval for the population mean based on a sample set having a small number of values (n) with a mean of ![]() and a variance of S.
and a variance of S.
4.4 TESTING THE VALIDITY OF THE CONFIDENCE INTERVAL
A test that demonstrates the validity of the theory of the confidence interval is illustrated as follows. Using a computer and normal random number generating software, 1000 sample data sets of 16 values each were collected randomly from a population with mean μ = 25.4 and standard error σ = ±1.3. Using a 95% confidence interval (α = 0.05) and Equation (4.7), the interval for the population mean derived for each sample set was computed and compared with the actual population mean. If the theory is valid, the interval constructed is expected to contain the population's mean 95% of the time based on the confidence level of 0.05. Appendix E shows the 95% intervals computed for the 1000 samples. The intervals not containing the population mean of 25.4 are marked with an asterisk. From the data tabulated, it is seen that 50 of 1000 sample sets failed to contain the population mean. This corresponds to exactly 5% of the samples. In other words, the proportion of samples that enclose the mean is exactly 95%. This demonstrates that the bounds calculated by Equation (4.7), in fact, enclose the population mean at the confidence level selected.
4.5 SELECTING A SAMPLE SIZE
A common problem encountered in surveying practice is to determine the necessary number of repeated observations to meet a specific precision. In practice, the size of S cannot be controlled absolutely. Rather, as seen in Equation (4.7), the confidence interval can be controlled only by varying the number of repeated observations. In general, the larger the sample size, the smaller the confidence interval. From Equation (4.7), the range in which the population mean (μ) resides at a selected level of confidence (α) is

Now let I represent one-half of the interval in which the population mean lies. Then from Equation (b), I is
Rearranging Equation (4.9)
In Equation (4.10), n is the number of repeated measurements, I the desired confidence interval, tα/2 the t value based on the number of degrees of freedom (v), and S the sample set standard deviation. In the practical application of Equation (4.10), tα/2 and S are unknown since the data set has yet to be collected. Also, the number of observations, and thus the number of redundancies, is unknown, since they are the computational objectives in this problem. Therefore, Equation (4.10) must be modified to use the standard normal random variable, z, and its critical value of E, which is not dependent on v or n; that is
where n is the number of repetitions, tα/2 the E value determined from the standard normal distribution table (Table D.1), σ an estimated value for the standard error of the measurement, and I the desired confidence interval.
4.6 CONFIDENCE INTERVAL FOR A POPULATION VARIANCE
![]() From Equation (4.1),
From Equation (4.1), ![]() , and thus confidence intervals for the variance of the population, σ2, are based on the χ2 statistic, sample variance, and its degrees of freedom. Percentage points (areas) for the upper and lower tails of the χ2 distribution are tabulated in Table D.2. This table lists values (denoted by
, and thus confidence intervals for the variance of the population, σ2, are based on the χ2 statistic, sample variance, and its degrees of freedom. Percentage points (areas) for the upper and lower tails of the χ2 distribution are tabulated in Table D.2. This table lists values (denoted by ![]() ) that determine the upper boundary for areas from
) that determine the upper boundary for areas from ![]() to +∞ of the distribution, such that
to +∞ of the distribution, such that
for a given number of redundancies, v. Unlike the normal distribution and the t distribution, the ![]() distribution is not symmetric about zero. To locate an area in the lower tail of the distribution, the appropriate value of
distribution is not symmetric about zero. To locate an area in the lower tail of the distribution, the appropriate value of ![]() must be found, where
must be found, where ![]() . These facts are used to construct a probability statement for χ2 as:
. These facts are used to construct a probability statement for χ2 as:
where ![]() and
and ![]() are tabulated in Table D.2 by the number of redundant observations. Substituting Equation (4.1) into Equation (4.12) yields
are tabulated in Table D.2 by the number of redundant observations. Substituting Equation (4.1) into Equation (4.12) yields

Recalling a property of mathematical inequalities, that in taking the reciprocal of a function the inequality is reversed, it follows that
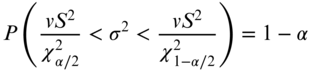
Thus, the (1 − α) confidence interval for the population variance (σ2) is
The ![]() distribution is often used to see if the reference variance from a least squares adjustment is statistically equal to one. As you will learn in Chapters 5 and 16, a two-tailed statistical test, which is equivalent to this confidence, is often used. This test is known as the goodness of fit test. However, some software packages simply list the reference variance and the range of the confidence interval provided by Equation (4.15) at a user-specified confidence level. The user must then check to see if the reference variance computed from the adjustment is in the confidence interval provided.
distribution is often used to see if the reference variance from a least squares adjustment is statistically equal to one. As you will learn in Chapters 5 and 16, a two-tailed statistical test, which is equivalent to this confidence, is often used. This test is known as the goodness of fit test. However, some software packages simply list the reference variance and the range of the confidence interval provided by Equation (4.15) at a user-specified confidence level. The user must then check to see if the reference variance computed from the adjustment is in the confidence interval provided.
4.7 CONFIDENCE INTERVAL FOR THE RATIO OF TWO POPULATION VARIANCES
Another common statistical procedure used is to compare the ratio of two population variances. The sampling distribution of the ratio of ![]() is well known when samples are collected randomly from a normal population. The confidence interval for
is well known when samples are collected randomly from a normal population. The confidence interval for ![]() is based on the F distribution using Equation (4.3) as
is based on the F distribution using Equation (4.3) as

Substituting Equation (4.1) and reducing yields

To establish a confidence interval for the ratio, the lower and upper values corresponding to the tails of the distribution must be found. A probability statement to find the confidence interval for the ratio is constructed as follows.
Rearranging yields
where ![]() and
and ![]() Substituting Equation (4.4) into (4.17) yields
Substituting Equation (4.4) into (4.17) yields
Thus from Equation (4.18), the (1 − α) confidence interval for the ![]() ratio is
ratio is
Notice that the degrees of freedom for the upper and lower limits in Equation (4.19) are opposite each other, and thus v2 is the numerator degrees of freedom and v1 is the denominator degrees of freedom in the upper limit.
An important situation where Equation (4.19) can be applied occurs in the analysis and adjustment of horizontal control surveys. During least squares adjustments of these types of surveys, control stations fix the data in space both positionally and rotationally. When observations tie into more than a minimal amount of control stations, the control coordinates must be mutually consistent. If they are not, any attempt to adjust the observations to the control will warp the data to fit the discrepancies in the control. A method for isolating control stations that are not consistent is to first do a least squares adjustment using only enough control to fix the data both positionally and rotationally in space. This is known as a minimally constrained adjustment, which is sometimes called a free adjustment. In traverse surveys, this means that one station must have fixed coordinates and one line must be fixed in direction. This adjustment is then followed with an adjustment using all available control. If the control information is consistent, the reference variance (![]() ) from the minimally constrained adjustment should be statistically equivalent to the reference variance (
) from the minimally constrained adjustment should be statistically equivalent to the reference variance (![]() ) obtained when using all control information (a constrained adjustment). That is, the ratio of
) obtained when using all control information (a constrained adjustment). That is, the ratio of ![]() should be equal to 1.
should be equal to 1.
4.8 SOFTWARE
The tables in Appendix D are limiting in relationship to the number of degrees of freedom and percentage points. These limitations can often be overcome with software. For example, the t distribution does not contain the required column for determining a 99.7% confidence interval or a row for 43 degrees of freedom. STATS, which is available on the companion website for this book, is capable of determining the critical t value for this interval. To do this using STATS, select the t distribution option from the statistics menu as shown in Figure 4.5. The software will request the necessary information from the user as shown in Figure 4.6, and return the critical t value as shown in Figure 4.7. Similar procedures can be used to determine the critical values for the χ2 and F distributions. STATS can also compute confidence intervals at selected probability levels. Figure 4.8 shows the entry screen for Example 4.1. As can be seen the sample mean, standard deviation, number of observations, and confidence level are entered. Notice that the confidence level is entered as a percentage. In this example, 95 is entered for the confidence level. Upon selecting the OK button, the software displays the computed confidence interval as shown in Figure 4.9. Similarly, confidence intervals for observations, the population variance, and the ratio of two population variances can be computed using STATS.

FIGURE 4.5 Selecting the t distribution from the ADJUST statistics menu.

FIGURE 4.6 Entering the upper-tail percentage points and degrees of freedom for the t-distribution critical value.

FIGURE 4.7 Computed critical value from a t distribution for a 99.7% confidence interval with 43 degrees of freedom.

FIGURE 4.8 Entry of data from Example 4.1 into STATS to compute a confidence interval.

FIGURE 4.9 Confidence interval computed from STATS for Example 4.1.
Spreadsheets can also be used to determine the critical values for distributions. For example in Microsoft Excel®, the function tinv(α, degrees of freedom) can be used to determine the critical t value. However, this function requires the overall percentage points from +∞ to be entered. Thus, to find the critical t value for a 99.7% confidence interval with 43 degrees of freedom, the appropriate expression would be tinv(0.003, 43) where 0.003 represents the sum of the lower- and upper-tail areas. In Excel®, the χ2 distribution function is chiinv(α, degrees of freedom). However, this function requires the upper and lower percentage points for α, which is 0.0015 and 0.9985 for a 99.7% confidence interval. Finally, the F distribution critical values can be determined using the function finv(α, v1, v2) where the function requires the appropriate percentage points for α, which is 0.0015 in this example, v1 are the number of degrees of freedom for the numerator variance, and v2 are the number of degrees of freedom for the denominator variance. These three functions can be used to reproduce the tables in Appendix D.
Mathcad® can also be used to generate the various critical values not shown in the Appendix D tables. Chapter 4 of the e-book written for Mathcad® that accompanies this book demonstrates the use of these functions while recreating the examples presented in this chapter. Unlike the spreadsheet and the tables in this book, Mathcad® takes the probability and degrees of freedom for its input. For example, the critical value from the t distribution for a 99.7% confidence interval with 43 degrees of freedom is computed as t := qt(0.9985, 43), where 0.9985 is determined from the area under the t distribution curve going from −∞ to the upper-tail bounds; that is, it is ![]() where α is 0.003. Similarly, the χ2 critical values are computed by calling the function qchisq(p, df) where p is the probability as defined previously and df are the number of degrees of freedom for the variance. F distribution critical values are determined by calling the function qF(p, df1, df2) where p is the probability as defined previously, df1 are the number of degrees of freedom for the numerator variance, and df2 are the number of degrees of freedom for the denominator variance.
where α is 0.003. Similarly, the χ2 critical values are computed by calling the function qchisq(p, df) where p is the probability as defined previously and df are the number of degrees of freedom for the variance. F distribution critical values are determined by calling the function qF(p, df1, df2) where p is the probability as defined previously, df1 are the number of degrees of freedom for the numerator variance, and df2 are the number of degrees of freedom for the denominator variance.
PROBLEMS
Note: Partial answers to problems marked with an asterisk are given in Appendix H.
- 4.1 What is the estimator function for the population mean?
- 4.2 Use the χ2 distribution table (Table D.2) to determine the critical values from the χ2 distribution that would be used to construct confidence intervals for a population variance for the following combinations:
- *(a) α = 0.10, v = 3
- (b) α = 0.05, v = 15
- (c) α = 0.01, v = 15
- (d) α = 0.05, v = 20
- 4.3 Use the t distribution table (Table D.3) to determine the critical value from the t distribution that would be used to construct confidence intervals for a population mean for each of the following combinations:
- *(a) α = 0.10, v = 3
- (b) α = 0.01, v = 10
- (c) α = 0.05, v = 15
- (d) α = 0.01, v = 20
- 4.4 Use the F distribution table (Table D.4) to determine the critical values from the F distribution that would be used to construct confidence intervals for the ratio of two sample variances for each of the following combinations:
- *(a) α = 0.20, v1 = 20, v2 = 5
- (b) α = 0.10, v1 = 15, v2 = 8
- (c) α = 0.05, v1 = 30, v2 = 10
- (d) α = 0.01, v1 = 10, v2 = 20
- 4.5 What is the computed χ2 value for the following conditions?
- *(a) v = 5, S2 = 1.23, and σ2 = 1.00
- (b) v = 8, S2 = 0.89, and σ2 = 1.00
- (c) v = 10, S2 = 0.65, and σ2 = 1.00
- (d) v = 15, S2 = 1.56, and σ2 = 1.00
- 4.6 A least squares adjustment is computed twice on a data set. When the data are minimally constrained with 10 degrees of freedom, a variance of 1.07 is obtained. In the second run, the constrained network has 13 degrees of freedom with a variance of 1.56. The a priori estimate for the reference variances (population variances) in both adjustments are one; that is,
 .
.
- (a) What is the 95% confidence interval for the reference variance in the minimally constrained adjustment? The population variance is one. Does this interval contain one?
- (b) What is the 95% confidence interval for the reference variance in the constrained adjustment? The population variance is one. Does this interval contain one?
- (c) What is the 95% confidence interval for the ratio of the two variances? Is there reason to be concerned about the consistency of the control? Statistically justify your response.
- 4.7 Repeat Problem 4.6 where the minimally constrained adjustment has 20 degrees of freedom, a standard deviation of 0.65 is obtained, and the constrained adjustment has 24 degrees of freedom with a standard deviation of 2.02. Use a 99% confidence interval.
- 4.8 The calibrated length of a baseline is 102.167 m. A properly reduced average distance of 102.162 m with a standard deviation of ±0.0031 m is computed after the line is observed eight times with an EDM.
- *(a) What is the 95% confidence interval for the measurements?
- (b) At a 95% level of confidence, can you state that the EDM is working properly? Statistically justify your response.
- 4.9 Repeat Problem 4.8 using a calibrated baseline of 1200.001 m and an observed length of 1200.006 with a standard deviation of ±0.0038 m after the line is observed 10 times with an EDM.
- 4.10 Repeat Problem 4.8 at 99%.
- 4.11 Repeat Problem 4.9 at 99%.
- 4.12 Develop a 95% confidence interval for the data in Problem 3.18, and determine if any observations may be rejected as outliers.
- 4.13 Develop a 99% confidence interval for the data in Problem 3.19, and determine if any observations may be rejected as outliers.
- *4.14 An observer's pointing and reading standard deviation is determined to be ±2.4″ after pointing and reading the circles of a particular instrument 8 times (n = 8). What is the 99% confidence interval for the population variance?
- 4.15 An observer's pointing and reading standard deviation is determined to be ±2.2″ after pointing and reading the circles of a particular instrument 8 times (n = 8). What is the 95% confidence interval for the population variance?
- 4.16 Repeat Problem 4.14 at 95%.
- 4.17 Repeat Problem 4.15 at 99%.
- 4.18 Was the observer in Problem 4.15 statistically better than the observer in Problem 4.14 at a
- *(a) 90% level of confidence?
- (b) 99% level of confidence?
- 4.19 Using sample statistics and the data in Example 3.1, construct a 99% confidence interval:
- (a) For the data and identify any observations that may be outliers.
- (b) For the population variance.
- 4.20 Using sample statistics and the data in Example 3.2, construct a 99% confidence interval:
- (a) For the data and identify any observations that may be outliers.
- (b) For the population variance.
- 4.21 For the data in Problem 3.16, construct a 99% confidence interval for the ratio of the two variances for Set 1 and 2. Are the variances statistically equal at this level of confidence? Justify your response.
- 4.22 Using sample statistics and the data from Problem 3.17, construct a 95% confidence interval:
- (a) For the data and identify any observations that may be outliers.
- (b) For the mean.
- 4.23 Using sample statistics (in feet) and the data from Problem 3.13, construct the appropriate 95% confidence interval and
- (a) Identify any observations that may be identified as possible outliers in the data.
- (b) If the length observed in Problem 3.13 was part of a calibration baseline with a published length of 485.603 ft, and the reported distances were properly reduced to their ground marks, is the instrument working properly at a 95% level of confidence?
- (c) If the manufacturer specifications for this instrument indicate that a distance of this length should have a variance of 0.000025, is the precision of the instrument meeting the specifications at a 95% level of confidence?
- 4.24 Use STATS to determine the critical values from the χ2 distribution that would be used to construct a 95% confidence interval for a population variance when there are 46 degrees of freedom.
- 4.25 Use STATS to determine the critical value from the t distribution that would be used to construct a 99.7% confidence interval for a population mean when there are 16 degrees of freedom.
- 4.26 Use STATS to determine the critical values from the F distribution that would be used to construct a 99.7% confidence interval for the ratio of two sample variances when v1 = 19 and v2 = 23.
- 4.27 Describe a method used to determine if the control station coordinates are inconsistent with the observations.














